一 哈夫曼树介绍
1. 关键名词
路径:
在一棵树种,一个节点到另一个节点之间的通路,称为路径。
路径的长度:
在一条路径中,每经过一个节点,路径长度都要加1。
节点的权:
给每一个节点赋予一个新的数值,被称为这个节点的权。
节点的带权路径长度:
指的是从根节点到该节点之间的路径长度与该节点的权的乘积。
WPL(树的带权路劲长度):
指树中所有叶子节点的带权路径长度之和。
2. 什么是赫夫曼树?
当用n个节点(都为叶子节点,且都有各自的权值)构建一棵二叉树时,如果构建的这棵二叉树的带权路径长度最小,则称为“最优二叉树”,也叫赫夫曼树,或者哈夫曼树。在构建哈弗曼树时,要使树的带权路径长度最小,只需要遵循一个原则,那就是:权重越大的结点离树根越近。
二 如何构建哈夫曼树
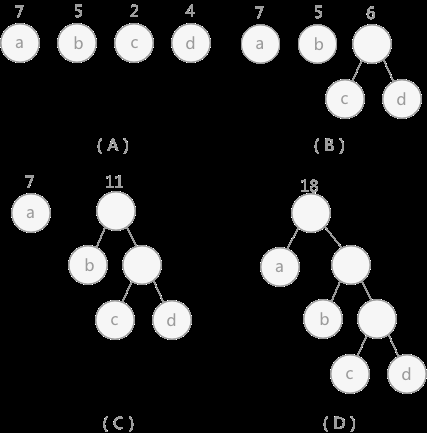
对于给定的有各自权值的 n 个结点,构建哈夫曼树有一个行之有效的办法:
- 在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和;
- 在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推;
重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树。
三 赫夫曼编码
哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%~90%之间。哈夫曼编码算法用字符在文件中出现的频率表来建立一个用0,1串表示各字符的最优表示方式。一个包含100,000个字符的文件,各字符出现频率不同,如下表所示。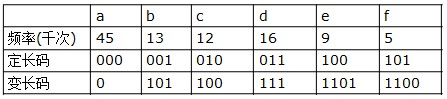
有多种方式表示文件中的信息,若用0,1码表示字符的方法,即每个字符用唯一的一个0,1串表示。若采用定长编码表示,则需要3位表示一个字符,整个文件编码需要300,000位;若采用变长编码表示,给频率高的字符较短的编码;频率低的字符较长的编码,达到整体编码减少的目的,则整个文件编码需要(45×1+13×3+12×3+16×3+9×4+5×4)×1000=224,000位,由此可见,变长码比定长码方案好,总码长减小约25%。
前缀码:对每一个字符规定一个0,1串作为其代码,并要求任一字符的代码都不是其他字符代码的前缀。这种编码称为前缀码。编码的前缀性质可以使译码方法非常简单;例如001011101可以唯一的分解为0,0,101,1101,因而其译码为aabe。
译码过程需要方便的取出编码的前缀,因此需要表示前缀码的合适的数据结构。为此,可以用二叉树作为前缀码的数据结构:树叶表示给定字符;从树根到树叶的路径当作该字符的前缀码;代码中每一位的0或1分别作为指示某节点到左儿子或右儿子的“路标”。

