基数排序不同于之前的各类排序，之前的排序方法或多或少的是通过使用比较和移动记录来实现排序，而基数排序的实现不需要进行对关键字的比较，只需要对关键字进行“分配”与“收集”两种操作即可完成。
基数排序的思想：桶排序思想。排序原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

一 案例说明什么是基数排序

例如对无序表{50，123，543，187，49，30，0，2，11，100}进行基数排序，由于每个关键字都是整数数值，且其中的最大值由个位、十位和百位构成，每个数位上的数字从 0 到 9，首先将各个关键字按照其个位数字的不同进行分配分配表如下图所示：

通过按照各关键字的个位数进行分配，按照顺序收集得到的序列变为：{50，30，0，100，11，2，123，543，187，49}。在该序列表的基础上，再按照各关键字的十位对各关键字进行分配，得到的分配表如下图所示：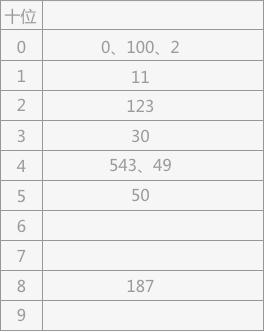

由上表顺序收集得到的记录表为：{0、100、2、11、123、30、543、49、50、187}。在该无序表的基础上，依次将表中的记录按照其关键字的百位进行分配，得到的分配如下图所示：

最终通过三次分配与收集，最终得到的就是一个排好序的有序表：{0、2、11、30、49、50、100、123、187、543}。
这个例子中是按照 个位 --》 十位 --》 百位的顺序进行基数排序，此种方式是从最低位开始排序，所以被称为最低位优先法（简称“LSD法”）。同样还可以按照 百位 --》 十位 --》 个位 的顺序进行排序，称为最高位优先法（简称“MSD法”），使用该方式进行排序同最低位优先法不同的是：当无序表中的关键字进行分配后，相当于进入了多个子序列，后序的排序工作分别在各个子序列中进行（最低位优先法每次分配与收集都是相对于整个序列表而言的）。
例如还是对{50，123，543，187，49，30，0，2，11，100}使用最高位优先法进行排序，首先按照百位的不同进行分配，得到的分配表为：

由上图所示，整个无序表被分为了 3 个子序列，序列 1 和序列 2 中含有多个关键字，序列 3 中只包含了一个关键字，最高位优先法完成排序的标准为：直到每个子序列中只有一个关键字为止，所以需要分别对两个子序列进行再分配，各自的分配表如下图所示：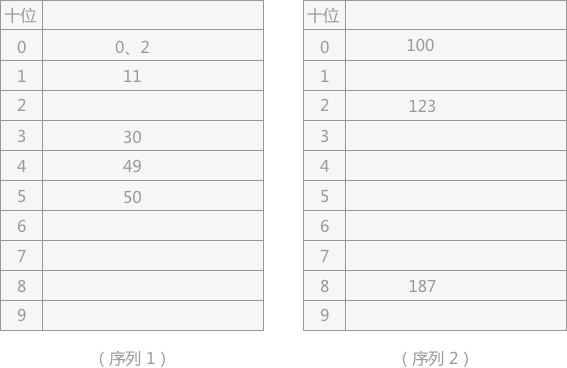

上表中，序列 1 中还有含有两个关键字的子序列，所以还需要根据个位进行分配，最终按照各子序列的顺序同样会得到一个有序表。

二 基数排序的应用场景

适用于数据量大但是范围小的场景，比如：
1.某大型企业数万员工的年龄排序
所有员工的年龄都在0~150之间
2.如何快速得知高考名次
所有人的分数都在 0~750之间

三 基数排序 vs 计数排序 vs 桶排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

• 基数排序：根据键值的每位数字来分配桶；
• 计数排序：每个桶只存储单一键值；
• 桶排序：每个桶存储一定范围的数值；

四 排序方式

基数排序有两种排序方式：

1. LSD法

LSD法排序思路：按照个位->十位->百位->...的顺序进行排序，这种从最低位开始排序的方式称为LSD法（最低位优先法）

2. MSD法

MSD法排序思路：按照...->百位->十位->个位的顺序进行排序，这种从最高位开始排序的方式称为最高位优先法（简称“MSD法”）。
使用该方式进行排序同最低位优先法不同的是：当无序表中的关键字进行分配后，相当于进入了多个子序列，后序的排序工作分别在各个子序列中进行（最低位优先法每次分配与收集都是相对于整个序列表而言的）。

四 基数排序的代码实现（采用LSD法）

package com.sort.s10RadixSort;
import org.junit.Test;
import java.util.Arrays;
public class RadixSort {
    public int[] sort(int[] sourceArray){
        if(null == sourceArray || sourceArray.length<2){
            return sourceArray;
        }
        // 对数组进行拷贝，不改变参数内容
        int[] arrToSort = Arrays.copyOf(sourceArray, sourceArray.length);
        // 获取整个数组值的最高位数
        int maxDigit = getMaxDigit(arrToSort);
        // 进行基数排序
        return radixSort(arrToSort, maxDigit);
    }
    private int[] radixSort(int[] arr, int maxDigit) {
        int mod = 10;// 每一位都由10个数构成：0/1/2/3/4/5/6/7/8/9
        int dev = 1;// dev 代表每次循环时的位数，个位就是1，十位为10，百位为100...
        // 采用的是LSD法：从最低位开始
        for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
            // 考虑负数的情况，这里扩展一倍队列数，其中 [0-9]对应负数，[10-19]对应正数 (bucket + 10)
            int[][] counter = new int[mod * 2][0];
            for (int j = 0; j < arr.length; j++) {
                // 根据当前计算的位数，来计算该放在哪一个桶中
                int bucket = ((arr[j] % mod) / dev) + mod;
                // 将值放入到对应的桶中
                counter[bucket] = arrayAppend(counter[bucket], arr[j]);
            }
            int pos = 0;
            // 将桶中的值按桶的顺序写回到原数组中
            for (int[] bucket : counter) {
                for (int value : bucket) {
                    arr[pos++] = value;
                }
            }
            println(arr);
        }
        return arr;
    }
    /** 获取数组中最高位数 */
    private int getMaxDigit(int[] arr) {
        // 获取最大值
        int maxValue = getMaxValue(arr);
        // 获取该最大值的位数
        return getNumLenght(maxValue);
    }
    /** 计算一个数值的位数 */
    protected int getNumLenght(long num) {
        if (num == 0) {
            return 1;
        }
        int lenght = 0;
        for (long temp = num; temp != 0; temp /= 10) {
            lenght++;
        }
        return lenght;
    }
    /** 获取数组中最大的值 */
    private int getMaxValue(int[] arr) {
        int maxValue = arr[0];
        for (int value : arr) {
            if (maxValue < value) {
                maxValue = value;
            }
        }
        return maxValue;
    }
    /** 自动扩容，并保存数据 */
    private int[] arrayAppend(int[] arr, int value) {
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = value;
        return arr;
    }
    /** 用于输出数组 */
    public void println(int [] a) {
        for(int x:a) {
            System.out.print(" "+x);
        }
        System.out.println("");
    }
    @Test
    public void testSort(){
        int[] nums = {5, 3, 4, 6, 7, 1, 2, 8, 4, 10, 100, 50, 30, 22, 34, 55, 43, 12, 31, 102, 105, 110,120,-110,-1,-10,-5,-15};
        RadixSort radixSort = new RadixSort();
        radixSort.println(radixSort.sort(nums));
    }
}