一 树的定义

树（tree）是包含n（n>=0）个节点的，具有层次关系的有穷集合。其中：
1. 每个元素称为节点，位于最上面的节点为根节点。
2. 除根节点之外的其余元素被分为m（m>=0）个互不相交的集合(T1，T2，…… Tn)，其中每一个集合Ti 本身也是一棵树，被称为子树。
树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的节点，所定义的关系称为父子关系。父子关系在树的节点之间建立了一个层次结构。在这种层次结构中有一个节点具有特殊的地位，这个节点称为该树的根节点，即树根。

二 树的特点

• 1. 每个节点有零个或多个子节点；
• 1. 没有父节点的节点称为根节点；
• 1. 每一个非根节点有且只有一个父节点；
• 1. 除了根节点外，每个子结点可以分为多个不相交的子树。
• 1. 当树的节点为0时，称为空树。

注意

1. 当n>0时，树的根节点时唯一的，不可能存在多个根节点，即一棵树有且只有一个根节点。
2. 当m>0时，子树的个数没有限制，但它们一定树互不相交的。

三 树的相关术语

1. 度

一个节点含有的子节点的个数称为度。

2. 叶子节点

度为0的节点称为叶子节点，又叫终端节点。即不存在子节点的节点为叶子节点。

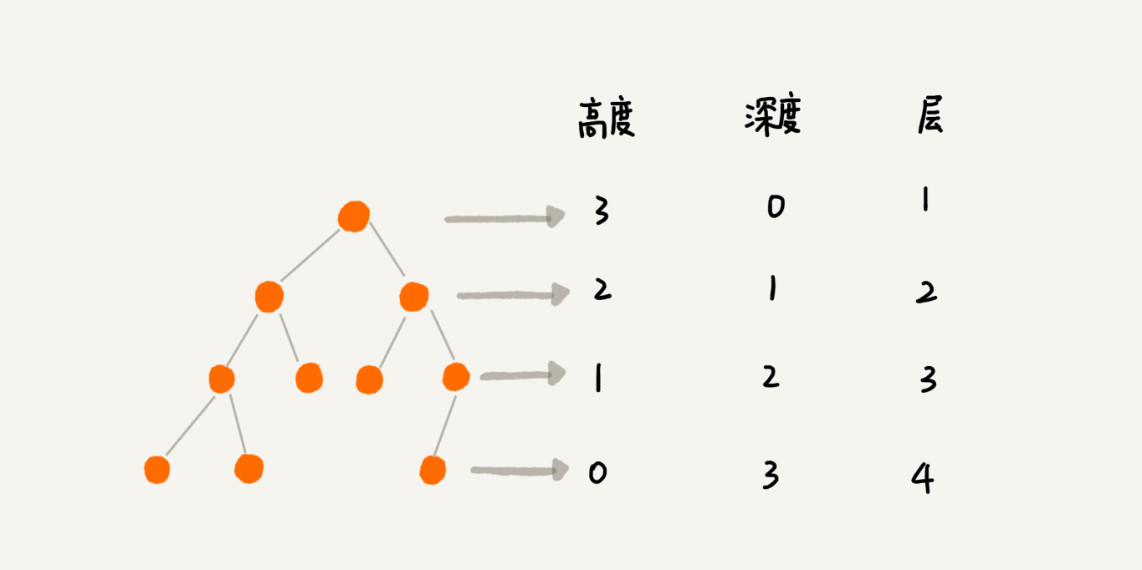
3. 高度

节点的高度：节点到叶子节点的最长路劲（边数）。
树的高度：根节点的高度，即根节点到叶子节点的最长路径。（空树高度为-1；仅含根节点的树高度为0）

4. 深度

节点的深度：根节点到这个节点所经历的边的个数。
树的深度：最深的叶节点的深度就是树的深度。（有的地方又说是根节点的深度）

5. 层

节点的层数：节点的深度+1（从根开始定义：根为第一层，根的子节点为第二层）。

四 有序树和无序树

如果将树中节点的各子树看成从左至右是有次序的，不能互换的，则成该树为有序树（OrderedTree）。否则称为无序树（UnorderedTree）。在未特别指明的情况下，所讨论的树都是有序树。

五 树的存储结构

简单的顺序存储不能满足树的实现，可以结合顺序存储和链式存储来实现：1.双亲表示法 2.孩子表示法 3.孩子兄弟表示法 4.最终实现方法（把每个节点的孩子节点排列起来，以单链表作为存储结构，则n各节点有n个孩子链表，如果是叶子节点，则此链表为空。然后n个头指针又组成一个线性表，采用顺序存储结构，放在一个一维数组终。）

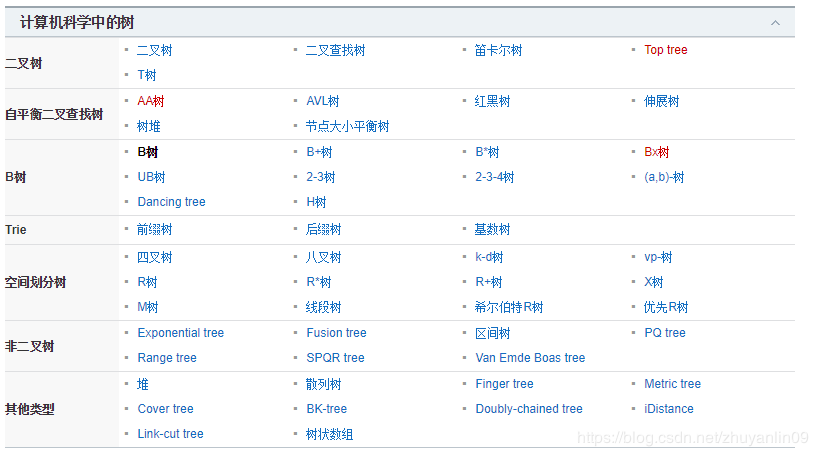
六 树的分类