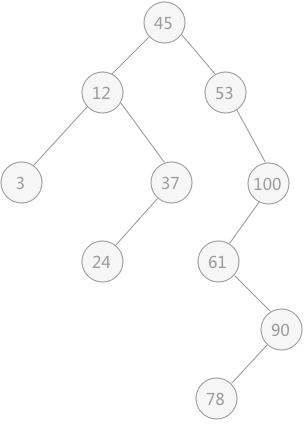
我们都知道散列表的插入、删除、查找操作的时间复杂度可以做到常量级的O(1),非常高效。而二叉查找树在比较平衡的情况下,插入、删除、查找操作时间复杂度才是O(logn),相对散列表,好像并没有什么优势,那我们为什么还要用二叉查找树呢?
第一,散列表中的数据是⽆序存储的,如果要输出有序的数据,需要先进行排序。而对于二叉查找树来说,我们只需要中序遍历,就可以在O(n)的时间复杂度内,输出有序的数据序列。
第二,散列表扩容耗时很多,而且当遇到散列冲突时,性能不稳定,尽管二叉查找树的性能不稳定,但是在工程中,我们最常用的平衡二叉查找树的性能非常稳定,时间复杂度稳定在O(logn)。
第三,笼统地来说,尽管散列表的查找等操作的时间复杂度是常量级的,但因为哈希冲突的存在,这个常量不一定比logn小,所以实际的查找速度可能不一定比(logn)快。加上哈希函数的耗时,也不一定就比平衡二叉查找树的效率高。
第四,散列表的构造要比二叉查找树要复杂,需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题,而且这个问题的解决方案比较成熟、固定。
第五,为了避免过多的散列冲突,散列表装载因子不能太大,特别是基于开放寻址法解决冲突的散列表,不然会浪费一定的存储空间。
我们在实际的开发过程中,需要结合具体的需求来选择使用哪一个数据结构。
一 二叉查找树的特点
二叉查找树又称为二叉排序树,其最大的特点就是支持动态数据集合的快速插入、删除、查找操作。
二叉查找树要么是空二叉树,要么具有如下特性:
- 如果其根结点有左子树,那么左子树上所有结点的值都小于根结点的值;- 如果其根结点有右子树,那么右子树上所有结点的值都大小根结点的值;- 每个节点的左右子树也要求都是二叉排序树;
二 使用二叉排序树查找关键字
二叉排序树中查找某关键字时,查找过程类似于次优二叉树,在二叉排序树不为空树的前提下,首先将被查找值同树的根结点进行比较,会有 3 种不同的结果:
- 如果相等,查找成功;
- 如果比较结果为根结点的关键字值较大,则说明该关键字可能存在其左子树中;
- 如果比较结果为根结点的关键字值较小,则说明该关键字可能存在其右子树中;
三 二叉排序树中插入关键字
二叉排序树本身是动态查找表的一种表示形式,有时会在查找过程中插入或者删除表中元素,当因为查找失败而需要插入数据元素时,该数据元素的插入位置一定位于二叉排序树的叶子结点,并且一定是查找失败时访问的最后一个结点的左孩子或者右孩子。
一个无序序列可以通过构建一棵二叉排序树,从而变成一个有序序列。
四 二叉排序树中删除关键字
如果在使用二叉排序树中删除某个数据元素时,需要在成功删除该结点的同时,依旧使这棵树保持为二叉排序树。
假设要删除的为结点 p,则对于二叉排序树来说,需要根据结点 p 所在不同的位置作不同的操作,有以下 3 种可能:
1. 删除结点 p 为叶子结点
2. 结点 p 只有左子树或者只有右子树
如果 p 是其双亲节点的左孩子,则直接将 p 节点的左子树或右子树作为其双亲节点的左子树;
反之如果 p 是其双亲节点的右孩子,则直接将 p 节点的左子树或右子树作为其双亲节点的右子树;
3. 结点 p 左右子树都有
结点 p 左右子树都有,此时有两种处理方式:
1)令结点 p 的左子树为其双亲结点的左子树;结点 p 的右子树为其自身直接前驱结点的右子树,如图所示: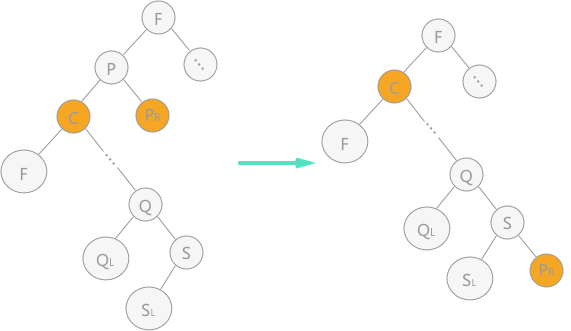
2)用结点 p 的直接前驱(或直接后继)来代替结点 p,同时在二叉排序树中对其直接前驱(或直接后继)做删除操作。如图所示: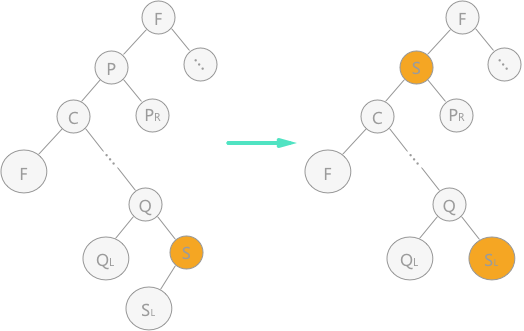
五 总结
使用二叉排序树时,即使查找表中各数据元素完全相同,但是不同的排列顺序,构建出的二叉排序树大不相同。例如:查找表 {45,24,53,12,37,93} 和表 {12,24,37,45,53,93} 各自构建的二叉排序树图下图所示: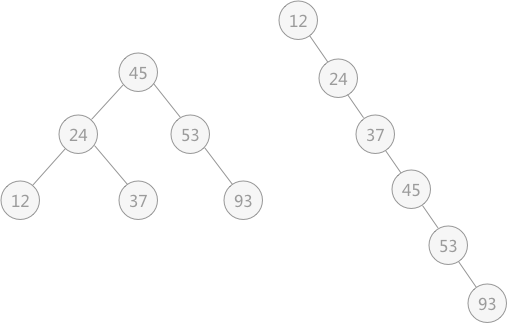
使用二叉排序树实现动态查找操作的过程,实际上就是从二叉排序树的根结点到查找元素结点的过程,所以时间复杂度同被查找元素所在的树的深度(层次数)有关。
为了弥补二叉排序树构造时产生如上图右侧所示的链式结构后影响算法效率的因素,需要对二叉排序树做“平衡化”处理,使其成为一棵平衡二叉树。