一 二叉树定义

1. 二叉树

二叉树是n个节点的有限集合，该集合或者为空集（称为空二叉树）；
或者由一个根节点和两个互不交互的左子树和右子树组成；

2. 满二叉树

在一棵二叉树中，如果所有分支节点都存在左子树和右子树，并且所有叶子节点都在同一层上，这样的二叉树称为满二叉树。

3. 完全二叉树

对一棵具有n个节点二叉树按层序编号，如果编号为 i（i <=n）的节点与同样深度的满二叉树中编号为 i 的节点在二叉树中的位置完全相同，则这样的二叉树称为完全二叉树。
即：叶子结点都在最底下两层，最后一层的叶子结点都靠左排列；并且除了最后一层，其它层的节点个数都要达到最大个数；
注意：满二叉树一定是完全二叉树，但完全二叉树不是满二叉树

4. 斜树：特殊的二叉树

左斜树：所有节点都只有左子树
右斜树：所有节点都只有右子树

二 二叉树的特点

• 性质（1）：在二叉树的第 i 层上，至多有 2^(i - 1) 个节点（ i>=1）；
• 性质（2）：深度为 k 的二叉树至多有 2^(k-1) 个节点（k>=1）;
• 性质（3）：对任何一颗二叉树T，如果其终端结点数为n0,度为2的结点数为n2，则n0 = n2+1。即：叶子节点数-1 就等于 度数为2 的节点数；
• 性质（4）：具有n个结点的完全二叉树深度为[log2n]+1 ([x]表示不大于x的最大整数)；
• 性质（5）：如果对一棵有n个结点的完全二叉树（其深度为[log2n]+1）的结点按层序编号（从第1层到第[log2n]+1层，每层从左到右）

那么对任意一个结点i(1<=i<=n)有：

• 1）如果i=1,则结点i是二叉树的根，无双亲；如果i>1,则其双亲是结点[i/2]
• 2）如果2i>n,则结点i无左孩子（结点i为叶子结点）；否则其左孩 子是结点2i。
• 3）如果2i+1>n,则结点i无右孩子；否则其右孩子是结点2i+1。

三 二叉树的存储结构

1. 顺序存储结构

用数组来存储，对于完全二叉树，如果节点 X 存储在数组中的下标为（i），那么：

• 它的左子节点的存储下标为（2i）
• 它的右子节点的存储下标为（2i+1）
• 它的父节点的存储下标为（i/2）

注意：
根节点存储在下标为1的位置。
完全二叉树用数组来存储是最省内存的方式。

2. 链式存储结构

节点存储在节点的类中，每个类中有3个属性，其中一个属性存储该节点的数据，另外两个属性分别指向左右子节点的指针。我们只需要在树的类中保存根节点的位置，就可以通过其左右子节点来将整棵树串起来。这种存储方式是比较常用的，大部分二叉树代码都是通过这种方式实现的。

四 二叉树的遍历

遍历的时间复杂度是0（n）

1. 前序遍历

如果是二叉树为空，则遍历操作直接返回，否则从根节点开始，遍历顺序：

  - 1.先访问根节点
  - 2.然后递归前序遍历左子树
  - 3.再递归前序遍历右子树

即：前序遍历是遍历的树及子树的根节点都最先输出。

voidProOrderTraverse(Tree T){
    if(T == null){
        return;
    }
    printf(“%c”,T.data);
    ProOrderTraverse(T.lchild);
    ProOrderTraverse(T.rchild);
}

2. 中序遍历

如果是二叉树为空，则遍历操作直接返回，否则从根节点开始（注意：并不是先访问根节点）

  - 1.先递归中序遍历根节点的左子树
  - 2.然后访问根节点
  - 3.再递归中序遍历根节点的右子树

即：中序遍历是遍历的树及子树的根节点都放于中间输出。

voidProOrderTraverse(Tree T){
    if(T == null){
        return;
    }
    ProOrderTraverse(T.lchild);
    printf(“%c”,T.data);
    ProOrderTraverse(T.rchild);
}

3. 后序遍历

如果是二叉树为空，则遍历操作直接返回，否则从根节点开始（注意：并不是先访问根节点）

  - 1.先递归后序遍历根节点的左子树
  - 2.再递归后序遍历根节点的右子树
  - 3.最后访问根节点

即：后序遍历是遍历的树及子树的根节点都放于最后输出。

voidProOrderTraverse(Tree T){
    if(T == null){
        return;
    }
    ProOrderTraverse(T->lchild);
    ProOrderTraverse(T->rchild);
    printf(“%c”,T-data);
}

4. 层序遍历

如果是二叉树为空，则遍历操作直接返回，否则从根节点开始访问，从上而下逐层遍历，在同一层，按从左到右的顺序对节点逐个访问。
推荐算法：先进先出队列的方式、广度优先搜索算法。

五 树、森林、二叉树的转换

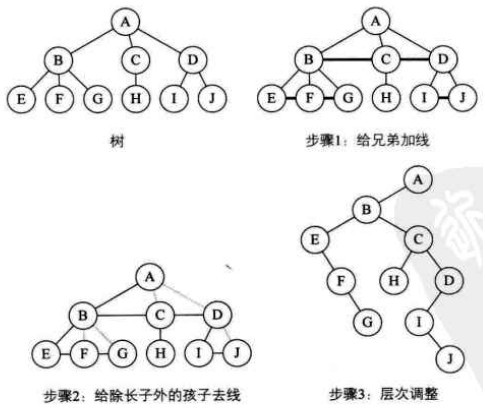
1. 树转换为二叉树

（1）加线。在所有的兄弟结点之间加一条线。
（2）去线。树中的每个结点，只保留它与第一个孩子结点的连线，删除其他孩子结点之间的连线。
（3）调整。以树的根结点为轴心，将整个树调节一下（第一个孩子是结点的左孩子，兄弟转过来的孩子是结点的右孩子）

2. 森林转换为二叉树

（1）把每棵树转换为二叉树
（2）第一棵二叉树不动，从第二棵二叉树开始，一次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子，用线连接起来。
转换规则：兄弟相连，长兄为父，孩子靠左。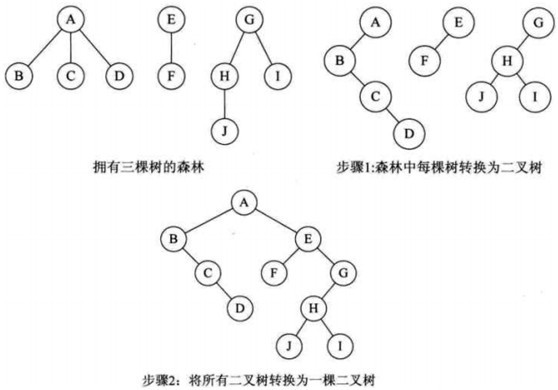

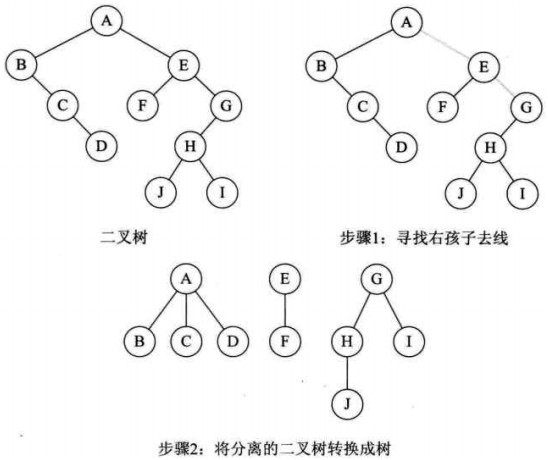
3. 二叉树转换为树

（1）加线。若某结点X的左孩子结点存在，则将这个左孩子的右孩子结点、右孩子的右孩子的右孩子结点。都作为结点X的孩子。将结点X与这些右孩子结点用线连接起来。
（2）去线。删除原二叉树中所有结点与其右孩子结点的连线。
（3）层次调整。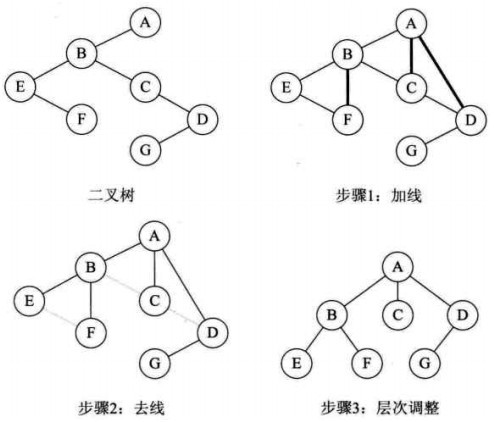

4. 二叉树转换为森林

前提： 假如一棵二叉树的根节点有右孩子，则这棵二叉树能够转换为森林，否则转换为一棵树。
转换规则：

• （1）从根节点开始，若右孩子存在，则把与右孩子结点的连线删除。再查看分离后的二叉树，若其根节点的右孩子存在，则连续删除。直到所有这些根结点与右孩子的连线都删除为止。
• （2）将每棵分离后的二叉树转换为树。