基本信息

0. 说明

学习到了卷积神经网络，写下一些随笔进行记录和回顾

1. 卷积基本概念

卷积核

就是一个不大的矩阵

互相关和卷积计算

就是对应相乘然后求和填进去的计算
互相关和卷积计算的区别简单的理解就是卷积核上下左右翻转，对于神经网络的训练没啥影响，计算反的最后的训练结果反正也是反的

3. 池化

池化其实就是为了解决过拟合的问题，把一块的数据用某一个数据进行代表
目前接触的池化层有最大池化层和平均池化层，顾名思义就是把最大值或者是平均值作为池化结果

4. 卷积网络

卷积网络往往是卷积层，激活函数，池化层进行搭配而形成的
卷积网络的最后可以是使用全连接层进行连接到输出的维度
在卷积层和全连接层之间的对接：

卷积层块的输出形状为(批量大小, 通道, 高, 宽)。当卷积层块的输出传入全连接层块时，全连接层块会将小批量中每个样本变平（flatten）。也就是说，全连接层的输入形状将变成二维，其中第一维是小批量中的样本，第二维是每个样本变平后的向量表示，且向量长度为通道、高和宽的乘积。全连接层块含3个全连接层。它们的输出个数分别是120、84和10，其中10为输出的类别个数。

具体的例子可见下附代码：cov是卷积层，最后的fc是全连接层

  1. class LeNet(nn.Module):
  2.     def __init__(self):
  3.         super(LeNet, self).__init__()
  4.         self.conv = nn.Sequential(
  5.             nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
  6.             nn.Sigmoid(),
  7.             nn.MaxPool2d(2, 2), # kernel_size, stride
  8.             nn.Conv2d(6, 16, 5),
  9.             nn.Sigmoid(),
  10.             nn.MaxPool2d(2, 2)
  11.         )
  12.         self.fc = nn.Sequential(
  13.             nn.Linear(16*4*4, 120),
  14.             nn.Sigmoid(),
  15.             nn.Linear(120, 84),
  16.             nn.Sigmoid(),
  17.             nn.Linear(84, 10)
  18.         )
  20.     def forward(self, img):
  21.         feature = self.conv(img)
  22.         output = self.fc(feature.view(img.shape[0], -1))
  23.         return output

5. 卷积理解与1*1卷积核

1*1的卷积核构成的卷积层可以看作是全连接层的变种
具体的理解也挺绕的，不过确实是来着
卷积的理解就是利用卷积核对目标数据进行特征的提取

6. 卷积的超参数

超参数包括卷积核大小，目标数据填充大小，输出输入通道，步长
目前不太能理解，但是对于查询的结果进行直观的理解就是，卷积核越大越能在较大的维度来提取数据，步长小的话会对数据进行重复的提取，加大计算量，但是步长太大又会有遗漏数据的问题。

二维卷积层输出的二维数组可以看作是输入在空间维度（宽和高）上某一级的表征，也叫特征图（feature map）。影响元素x的前向计算的所有可能输入区域（可能大于输入的实际尺寸）叫做x的感受野（receptive field）。以图5.1为例，输入中阴影部分的四个元素是输出中阴影部分元素的感受野。我们将图5.1中形状为2×2的输出记为Y，并考虑一个更深的卷积神经网络：将Y与另一个形状为2×2的核数组做互相关运算，输出单个元素z。那么，z在Y上的感受野包括Y的全部四个元素，在输入上的感受野包括其中全部9个元素。可见，我们可以通过更深的卷积神经网络使特征图中单个元素的感受野变得更加广阔，从而捕捉输入上更大尺寸的特征。 我们常使用“元素”一词来描述数组或矩阵中的成员。在神经网络的术语中，这些元素也可称为“单元”。当含义明确时，本书不对这两个术语做严格区分。

卷积网络

1.Le_Net

利用卷积层和sigmoid激活函数以及最大池化层结合构成卷积层，然后利用线性层和sigmoid激活函数搭建全连接层

  1. lass LeNet(nn.Module):
  2.     def __init__(self):
  3.         super(LeNet, self).__init__()
  4.         self.conv = nn.Sequential(
  5.             nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
  6.             nn.Sigmoid(),
  7.             nn.MaxPool2d(2, 2), # kernel_size, stride
  8.             nn.Conv2d(6, 16, 5),
  9.             nn.Sigmoid(),
  10.             nn.MaxPool2d(2, 2)
  11.         )
  12.         self.fc = nn.Sequential(
  13.             nn.Linear(16*4*4, 120),
  14.             nn.Sigmoid(),
  15.             nn.Linear(120, 84),
  16.             nn.Sigmoid(),
  17.             nn.Linear(84, 10)
  18.         )
  20.     def forward(self, img):
  21.         feature = self.conv(img)
  22.         output = self.fc(feature.view(img.shape[0], -1))
  23.         return output
  24. """
  25. LeNet(
  26.   (conv): Sequential(
  27.     (0): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  28.     (1): Sigmoid()
  29.     (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  30.     (3): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  31.     (4): Sigmoid()
  32.     (5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  33.   )
  34.   (fc): Sequential(
  35.     (0): Linear(in_features=256, out_features=120, bias=True)
  36.     (1): Sigmoid()
  37.     (2): Linear(in_features=120, out_features=84, bias=True)
  38.     (3): Sigmoid()
  39.     (4): Linear(in_features=84, out_features=10, bias=True)
  40.   )
  41. )
  42. """

2. Alex_Net

先利用较大的卷积核提取信息特征，然后逐渐的减小卷积核大小
差异于引用学习的来源https://tangshusen.me/Dive-into-DL-PyTorch/#/chapter05_CNN/5.6_alexnet

第一，与相对较小的LeNet相比，AlexNet包含8层变换，其中有5层卷积和2层全连接隐藏层，以及1个全连接输出层。下面我们来详细描述这些层的设计。

AlexNet第一层中的卷积窗口形状是11×11。因为ImageNet中绝大多数图像的高和宽均比MNIST图像的高和宽大10倍以上，ImageNet图像的物体占用更多的像素，所以需要更大的卷积窗口来捕获物体。第二层中的卷积窗口形状减小到5×5，之后全采用3×3。此外，第一、第二和第五个卷积层之后都使用了窗口形状为3×3、步幅为2的最大池化层。而且，AlexNet使用的卷积通道数也大于LeNet中的卷积通道数数十倍。

紧接着最后一个卷积层的是两个输出个数为4096的全连接层。这两个巨大的全连接层带来将近1 GB的模型参数。由于早期显存的限制，最早的AlexNet使用双数据流的设计使一个GPU只需要处理一半模型。幸运的是，显存在过去几年得到了长足的发展，因此通常我们不再需要这样的特别设计了。

第二，AlexNet将sigmoid激活函数改成了更加简单的ReLU激活函数。一方面，ReLU激活函数的计算更简单，例如它并没有sigmoid激活函数中的求幂运算。另一方面，ReLU激活函数在不同的参数初始化方法下使模型更容易训练。这是由于当sigmoid激活函数输出极接近0或1时，这些区域的梯度几乎为0，从而造成反向传播无法继续更新部分模型参数；而ReLU激活函数在正区间的梯度恒为1。因此，若模型参数初始化不当，sigmoid函数可能在正区间得到几乎为0的梯度，从而令模型无法得到有效训练。

第三，AlexNet通过丢弃法（参见3.13节）来控制全连接层的模型复杂度。而LeNet并没有使用丢弃法。

第四，AlexNet引入了大量的图像增广，如翻转、裁剪和颜色变化，从而进一步扩大数据集来缓解过拟合。我们将在后面的9.1节（图像增广）详细介绍这种方法。

  1. class AlexNet(nn.Module):
  2.     def __init__(self):
  3.         super(AlexNet, self).__init__()
  4.         self.conv = nn.Sequential(
  5.             nn.Conv2d(1, 96, 11, 4), # in_channels, out_channels, kernel_size, stride, padding
  6.             nn.ReLU(),
  7.             nn.MaxPool2d(3, 2), # kernel_size, stride
  8.             # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
  9.             nn.Conv2d(96, 256, 5, 1, 2),
  10.             nn.ReLU(),
  11.             nn.MaxPool2d(3, 2),
  12.             # 连续3个卷积层，且使用更小的卷积窗口。除了最后的卷积层外，进一步增大了输出通道数。
  13.             # 前两个卷积层后不使用池化层来减小输入的高和宽
  14.             nn.Conv2d(256, 384, 3, 1, 1),
  15.             nn.ReLU(),
  16.             nn.Conv2d(384, 384, 3, 1, 1),
  17.             nn.ReLU(),
  18.             nn.Conv2d(384, 256, 3, 1, 1),
  19.             nn.ReLU(),
  20.             nn.MaxPool2d(3, 2)
  21.         )
  22.          # 这里全连接层的输出个数比LeNet中的大数倍。使用丢弃层来缓解过拟合
  23.         self.fc = nn.Sequential(
  24.             nn.Linear(256*5*5, 4096),
  25.             nn.ReLU(),
  26.             nn.Dropout(0.5),
  27.             nn.Linear(4096, 4096),
  28.             nn.ReLU(),
  29.             nn.Dropout(0.5),
  30.             # 输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
  31.             nn.Linear(4096, 10),
  32.         )
  34.     def forward(self, img):
  35.         feature = self.conv(img)
  36.         output = self.fc(feature.view(img.shape[0], -1))
  37.         return output
  39. """
  40. Net Struct as follows: 
  41. AlexNet(
  42.   (conv): Sequential(
  43.     (0): Conv2d(1, 96, kernel_size=(11, 11), stride=(4, 4))
  44.     (1): ReLU()
  45.     (2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
  46.     (3): Conv2d(96, 256, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  47.     (4): ReLU()
  48.     (5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
  49.     (6): Conv2d(256, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  50.     (7): ReLU()
  51.     (8): Conv2d(384, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  52.     (9): ReLU()
  53.     (10): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  54.     (11): ReLU()
  55.     (12): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
  56.   )
  57.   (fc): Sequential(
  58.     (0): Linear(in_features=6400, out_features=4096, bias=True)
  59.     (1): ReLU()
  60.     (2): Dropout(p=0.5, inplace=False)
  61.     (3): Linear(in_features=4096, out_features=4096, bias=True)
  62.     (4): ReLU()
  63.     (5): Dropout(p=0.5, inplace=False)
  64.     (6): Linear(in_features=4096, out_features=10, bias=True)
  65.   )
  66. )
  68. """

3. VGG_Net

利用VGG块和全连接层进行对接

VGG块的组成规律是：连续使用数个相同的填充为1、窗口形状为3×3的卷积层后接上一个步幅为2、窗口形状为2×2的最大池化层。卷积层保持输入的高和宽不变，而池化层则对其减半。我们使用vgg_block函数来实现这个基础的VGG块，它可以指定卷积层的数量和输入输出通道数。

对于给定的感受野（与输出有关的输入图片的局部大小），采用堆积的小卷积核优于采用大的卷积核，因为可以增加网络深度来保证学习更复杂的模式，而且代价还比较小（参数更少）。例如，在VGG中，使用了3个3x3卷积核来代替7x7卷积核，使用了2个3x3卷积核来代替5*5卷积核，这样做的主要目的是在保证具有相同感知野的条件下，提升了网络的深度，在一定程度上提升了神经网络的效果。

  1. def vgg_block(num_convs, in_channels, out_channels):
  2.     blk = []
  3.     for i in range(num_convs):
  4.         if i == 0:
  5.             blk.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
  6.         else:
  7.             blk.append(nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1))
  8.         blk.append(nn.ReLU())
  9.     blk.append(nn.MaxPool2d(kernel_size=2, stride=2)) # 这里会使宽高减半
  10.     return nn.Sequential(*blk)
  11. def vgg(conv_arch, fc_features, fc_hidden_units=4096):
  12.     net = nn.Sequential()
  13.     # 卷积层部分
  14.     for i, (num_convs, in_channels, out_channels) in enumerate(conv_arch):
  15.         # 每经过一个vgg_block都会使宽高减半
  16.         net.add_module("vgg_block_" + str(i+1), vgg_block(num_convs, in_channels, out_channels))
  17.     # 全连接层部分
  18.     net.add_module("fc", nn.Sequential(FlattenLayer(),
  19.                                  nn.Linear(fc_features, fc_hidden_units),
  20.                                  nn.ReLU(),
  21.                                  nn.Dropout(0.5),
  22.                                  nn.Linear(fc_hidden_units, fc_hidden_units),
  23.                                  nn.ReLU(),
  24.                                  nn.Dropout(0.5),
  25.                                  nn.Linear(fc_hidden_units, 10)
  26.                                 ))
  27.     return net
  29. """
  30. Net Struct as follows: 
  31. Sequential(
  32.   (vgg_block_1): Sequential(
  33.     (0): Conv2d(1, 8, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  34.     (1): ReLU()
  35.     (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  36.   )
  37.   (vgg_block_2): Sequential(
  38.     (0): Conv2d(8, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  39.     (1): ReLU()
  40.     (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  41.   )
  42.   (vgg_block_3): Sequential(
  43.     (0): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  44.     (1): ReLU()
  45.     (2): Conv2d(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  46.     (3): ReLU()
  47.     (4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  48.   )
  49.   (vgg_block_4): Sequential(
  50.     (0): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  51.     (1): ReLU()
  52.     (2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  53.     (3): ReLU()
  54.     (4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  55.   )
  56.   (vgg_block_5): Sequential(
  57.     (0): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  58.     (1): ReLU()
  59.     (2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  60.     (3): ReLU()
  61.     (4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  62.   )
  63.   (fc): Sequential(
  64.     (0): FlattenLayer()
  65.     (1): Linear(in_features=3136, out_features=512, bias=True)
  66.     (2): ReLU()
  67.     (3): Dropout(p=0.5, inplace=False)
  68.     (4): Linear(in_features=512, out_features=512, bias=True)
  69.     (5): ReLU()
  70.     (6): Dropout(p=0.5, inplace=False)
  71.     (7): Linear(in_features=512, out_features=10, bias=True)
  72.   )
  73. )
  74. """

4. NiN_Net

NIN网络可以理解为是卷积网络和全连接层结合作为一个块，然后多个块进行连接
由于前面说过1*1的卷积核构造的卷积层就是一个全连接层，所以这里就是这样构造的.
还有一个不同

除使用NiN块以外，NiN还有一个设计与AlexNet显著不同：NiN去掉了AlexNet最后的3个全连接层，取而代之地，NiN使用了输出通道数等于标签类别数的NiN块，然后使用全局平均池化层对每个通道中所有元素求平均并直接用于分类。这里的全局平均池化层即窗口形状等于输入空间维形状的平均池化层。NiN的这个设计的好处是可以显著减小模型参数尺寸，从而缓解过拟合。然而，该设计有时会造成获得有效模型的训练时间的增加。

  1. def nin_block(in_channels, out_channels, kernel_size, stride, padding):
  2.     blk = nn.Sequential(nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding),
  3.                         nn.ReLU(),
  4.                         nn.Conv2d(out_channels, out_channels, kernel_size=1),
  5.                         nn.ReLU(),
  6.                         nn.Conv2d(out_channels, out_channels, kernel_size=1),
  7.                         nn.ReLU())
  8.     return blk
  9. class GlobalAvgPool2d(nn.Module):
  10.     # 全局平均池化层可通过将池化窗口形状设置成输入的高和宽实现
  11.     def __init__(self):
  12.         super(GlobalAvgPool2d, self).__init__()
  13.     def forward(self, x):
  14.         return F.avg_pool2d(x, kernel_size=x.size()[2:])
  16. net = nn.Sequential(
  17.     nin_block(1, 96, kernel_size=11, stride=4, padding=0),
  18.     nn.MaxPool2d(kernel_size=3, stride=2),
  19.     nin_block(96, 256, kernel_size=5, stride=1, padding=2),
  20.     nn.MaxPool2d(kernel_size=3, stride=2),
  21.     nin_block(256, 384, kernel_size=3, stride=1, padding=1),
  22.     nn.MaxPool2d(kernel_size=3, stride=2), 
  23.     nn.Dropout(0.5),
  24.     # 标签类别数是10
  25.     nin_block(384, 10, kernel_size=3, stride=1, padding=1),
  26.     GlobalAvgPool2d(), 
  27.     # 将四维的输出转成二维的输出，其形状为(批量大小, 10)
  28.     d2l.FlattenLayer())
  30. """
  31. Net Struct as follows: 
  32. Sequential(
  33.   (0): Sequential(
  34.     (0): Conv2d(1, 96, kernel_size=(11, 11), stride=(4, 4))
  35.     (1): ReLU()
  36.     (2): Conv2d(96, 96, kernel_size=(1, 1), stride=(1, 1))
  37.     (3): ReLU()
  38.     (4): Conv2d(96, 96, kernel_size=(1, 1), stride=(1, 1))
  39.     (5): ReLU()
  40.   )
  41.   (1): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
  42.   (2): Sequential(
  43.     (0): Conv2d(96, 256, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  44.     (1): ReLU()
  45.     (2): Conv2d(256, 256, kernel_size=(1, 1), stride=(1, 1))
  46.     (3): ReLU()
  47.     (4): Conv2d(256, 256, kernel_size=(1, 1), stride=(1, 1))
  48.     (5): ReLU()
  49.   )
  50.   (3): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
  51.   (4): Sequential(
  52.     (0): Conv2d(256, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  53.     (1): ReLU()
  54.     (2): Conv2d(384, 384, kernel_size=(1, 1), stride=(1, 1))
  55.     (3): ReLU()
  56.     (4): Conv2d(384, 384, kernel_size=(1, 1), stride=(1, 1))
  57.     (5): ReLU()
  58.   )
  59.   (5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
  60.   (6): Dropout(p=0.5, inplace=False)
  61.   (7): Sequential(
  62.     (0): Conv2d(384, 10, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  63.     (1): ReLU()
  64.     (2): Conv2d(10, 10, kernel_size=(1, 1), stride=(1, 1))
  65.     (3): ReLU()
  66.     (4): Conv2d(10, 10, kernel_size=(1, 1), stride=(1, 1))
  67.     (5): ReLU()
  68.   )
  69.   (8): GlobalAvgPool2d()
  70.   (9): FlattenLayer()
  71. )
  72. """

5. GoogLeNet

Inception块里有4条并行的线路。前3条线路使用窗口大小分别是1×1、3×3和5×5的卷积层来抽取不同空间尺寸下的信息，其中中间2个线路会对输入先做1×1卷积来减少输入通道数，以降低模型复杂度。第四条线路则使用3×3最大池化层，后接1×1卷积层来改变通道数。4条线路都使用了合适的填充来使输入与输出的高和宽一致。最后我们将每条线路的输出在通道维上连结，并输入接下来的层中去。

对于这里，我的理解就是这个网络把选择权交给了神经网络自己，由于采用了各种的卷积核，所以最后的参数的优化也是取决于网络自己。哪一个效果更好就用那一个

  1. class Inception(nn.Module):
  2.     # c1 - c4为每条线路里的层的输出通道数
  3.     def __init__(self, in_c, c1, c2, c3, c4):
  4.         super(Inception, self).__init__()
  5.         # 线路1，单1 x 1卷积层
  6.         self.p1_1 = nn.Conv2d(in_c, c1, kernel_size=1)
  7.         # 线路2，1 x 1卷积层后接3 x 3卷积层
  8.         self.p2_1 = nn.Conv2d(in_c, c2[0], kernel_size=1)
  9.         self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
  10.         # 线路3，1 x 1卷积层后接5 x 5卷积层
  11.         self.p3_1 = nn.Conv2d(in_c, c3[0], kernel_size=1)
  12.         self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
  13.         # 线路4，3 x 3最大池化层后接1 x 1卷积层
  14.         self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
  15.         self.p4_2 = nn.Conv2d(in_c, c4, kernel_size=1)
  17.     def forward(self, x):
  18.         p1 = F.relu(self.p1_1(x))
  19.         p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
  20.         p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
  21.         p4 = F.relu(self.p4_2(self.p4_1(x)))
  22.         return torch.cat((p1, p2, p3, p4), dim=1)  # 在通道维上连结输出
  1. b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
  2.                    nn.ReLU(),
  3.                    nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
  4. b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
  5.                    nn.Conv2d(64, 192, kernel_size=3, padding=1),
  6.                    nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
  7. b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
  8.                    Inception(256, 128, (128, 192), (32, 96), 64),
  9.                    nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
  10. b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
  11.                    Inception(512, 160, (112, 224), (24, 64), 64),
  12.                    Inception(512, 128, (128, 256), (24, 64), 64),
  13.                    Inception(512, 112, (144, 288), (32, 64), 64),
  14.                    Inception(528, 256, (160, 320), (32, 128), 128),
  15.                    nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
  16. b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
  17.                    Inception(832, 384, (192, 384), (48, 128), 128),
  18.                    d2l.GlobalAvgPool2d())
  20. net = nn.Sequential(b1, b2, b3, b4, b5, 
  21.                     d2l.FlattenLayer(), nn.Linear(1024, 10))
  23. """
  24. Net Struct as follows: 
  25. Sequential(
  26.   (0): Sequential(
  27.     (0): Conv2d(1, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3))
  28.     (1): ReLU()
  29.     (2): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
  30.   )
  31.   (1): Sequential(
  32.     (0): Conv2d(64, 64, kernel_size=(1, 1), stride=(1, 1))
  33.     (1): Conv2d(64, 192, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  34.     (2): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
  35.   )
  36.   (2): Sequential(
  37.     (0): Inception(
  38.       (p1_1): Conv2d(192, 64, kernel_size=(1, 1), stride=(1, 1))
  39.       (p2_1): Conv2d(192, 96, kernel_size=(1, 1), stride=(1, 1))
  40.       (p2_2): Conv2d(96, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  41.       (p3_1): Conv2d(192, 16, kernel_size=(1, 1), stride=(1, 1))
  42.       (p3_2): Conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  43.       (p4_1): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=False)
  44.       (p4_2): Conv2d(192, 32, kernel_size=(1, 1), stride=(1, 1))
  45.     )
  46.     (1): Inception(
  47.       (p1_1): Conv2d(256, 128, kernel_size=(1, 1), stride=(1, 1))
  48.       (p2_1): Conv2d(256, 128, kernel_size=(1, 1), stride=(1, 1))
  49.       (p2_2): Conv2d(128, 192, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  50.       (p3_1): Conv2d(256, 32, kernel_size=(1, 1), stride=(1, 1))
  51.       (p3_2): Conv2d(32, 96, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  52.       (p4_1): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=False)
  53.       (p4_2): Conv2d(256, 64, kernel_size=(1, 1), stride=(1, 1))
  54.     )
  55.     (2): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
  56.   )
  57.   (3): Sequential(
  58.     (0): Inception(
  59.       (p1_1): Conv2d(480, 192, kernel_size=(1, 1), stride=(1, 1))
  60.       (p2_1): Conv2d(480, 96, kernel_size=(1, 1), stride=(1, 1))
  61.       (p2_2): Conv2d(96, 208, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  62.       (p3_1): Conv2d(480, 16, kernel_size=(1, 1), stride=(1, 1))
  63.       (p3_2): Conv2d(16, 48, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  64.       (p4_1): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=False)
  65.       (p4_2): Conv2d(480, 64, kernel_size=(1, 1), stride=(1, 1))
  66.     )
  67.     (1): Inception(
  68.       (p1_1): Conv2d(512, 160, kernel_size=(1, 1), stride=(1, 1))
  69.       (p2_1): Conv2d(512, 112, kernel_size=(1, 1), stride=(1, 1))
  70.       (p2_2): Conv2d(112, 224, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  71.       (p3_1): Conv2d(512, 24, kernel_size=(1, 1), stride=(1, 1))
  72.       (p3_2): Conv2d(24, 64, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  73.       (p4_1): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=False)
  74.       (p4_2): Conv2d(512, 64, kernel_size=(1, 1), stride=(1, 1))
  75.     )
  76.     (2): Inception(
  77.       (p1_1): Conv2d(512, 128, kernel_size=(1, 1), stride=(1, 1))
  78.       (p2_1): Conv2d(512, 128, kernel_size=(1, 1), stride=(1, 1))
  79.       (p2_2): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  80.       (p3_1): Conv2d(512, 24, kernel_size=(1, 1), stride=(1, 1))
  81.       (p3_2): Conv2d(24, 64, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  82.       (p4_1): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=False)
  83.       (p4_2): Conv2d(512, 64, kernel_size=(1, 1), stride=(1, 1))
  84.     )
  85.     (3): Inception(
  86.       (p1_1): Conv2d(512, 112, kernel_size=(1, 1), stride=(1, 1))
  87.       (p2_1): Conv2d(512, 144, kernel_size=(1, 1), stride=(1, 1))
  88.       (p2_2): Conv2d(144, 288, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  89.       (p3_1): Conv2d(512, 32, kernel_size=(1, 1), stride=(1, 1))
  90.       (p3_2): Conv2d(32, 64, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  91.       (p4_1): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=False)
  92.       (p4_2): Conv2d(512, 64, kernel_size=(1, 1), stride=(1, 1))
  93.     )
  94.     (4): Inception(
  95.       (p1_1): Conv2d(528, 256, kernel_size=(1, 1), stride=(1, 1))
  96.       (p2_1): Conv2d(528, 160, kernel_size=(1, 1), stride=(1, 1))
  97.       (p2_2): Conv2d(160, 320, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  98.       (p3_1): Conv2d(528, 32, kernel_size=(1, 1), stride=(1, 1))
  99.       (p3_2): Conv2d(32, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  100.       (p4_1): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=False)
  101.       (p4_2): Conv2d(528, 128, kernel_size=(1, 1), stride=(1, 1))
  102.     )
  103.     (5): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
  104.   )
  105.   (4): Sequential(
  106.     (0): Inception(
  107.       (p1_1): Conv2d(832, 256, kernel_size=(1, 1), stride=(1, 1))
  108.       (p2_1): Conv2d(832, 160, kernel_size=(1, 1), stride=(1, 1))
  109.       (p2_2): Conv2d(160, 320, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  110.       (p3_1): Conv2d(832, 32, kernel_size=(1, 1), stride=(1, 1))
  111.       (p3_2): Conv2d(32, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  112.       (p4_1): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=False)
  113.       (p4_2): Conv2d(832, 128, kernel_size=(1, 1), stride=(1, 1))
  114.     )
  115.     (1): Inception(
  116.       (p1_1): Conv2d(832, 384, kernel_size=(1, 1), stride=(1, 1))
  117.       (p2_1): Conv2d(832, 192, kernel_size=(1, 1), stride=(1, 1))
  118.       (p2_2): Conv2d(192, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  119.       (p3_1): Conv2d(832, 48, kernel_size=(1, 1), stride=(1, 1))
  120.       (p3_2): Conv2d(48, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  121.       (p4_1): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=False)
  122.       (p4_2): Conv2d(832, 128, kernel_size=(1, 1), stride=(1, 1))
  123.     )
  124.     (2): GlobalAvgPool2d()
  125.   )
  126.   (5): FlattenLayer()
  127.   (6): Linear(in_features=1024, out_features=10, bias=True)
  128. )
  130. """

这里的另一个核心就是关于通道数配比的选择，这个应该也是超参数
反正不管了，大量的实验表明这样的配方好，那用就完事了

5. Batch_Normalization

原书的介绍很详细，但是这个介绍的更加详细
https://zhuanlan.zhihu.com/p/89422962
摘录部分

我们首先来思考一个问题，为什么神经网络需要对输入做标准化处理？原因在于神经网络本身就是为了学习数据的分布，如果训练集和测试集的分布不同，那么导致学习的神经网络泛化性能大大降低。同时，我们在使用mini-batch对神经网络进行训练时，不同的batch的数据的分布也有可能不同，那么网络就要在每次迭代都去学习适应不同的分布，这样将会大大降低网络的训练速度。因此我们需要对输入数据进行标准化处理。 对于深度网络的训练是一个复杂的过程，只要网络的前面几层发生微小的改变，那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变，那么这一层网络就需要去适应学习这个新的数据分布，所以如果训练过程中，训练数据的分布一直在发生变化，那么将会影响网络的训练速度。 网络一旦train起来，那么参数就要发生更新，除了输入层的数据外(因为输入层数据，我们已经人为的为每个样本归一化)，后面网络每一层的输入数据分布是一直在发生变化的，因为在训练的时候，前面层训练参数的更新将导致后面层输入数据分布的变化。我们把网络中间层在训练过程中，数据分布的改变称之为：Internal Covariate Shift（输入分布不稳定）。为了解决Internal Covariate Shift，便有了Batch Normalization的诞生。可以看到，在BN的计算过程中，不仅仅有标准化的操作，还有最后一步，被称为变换重构。为什么要增加这一步呢？其实如果是仅仅使用上面的归一化公式，对网络某一层A的输出数据做归一化，然后送入网络下一层B，这样是会影响到本层网络A所学习到的特征的。打个比方，比如网络中间某一层学习到特征数据本身就分布在S型激活函数的两侧，你强制把它给我归一化处理、标准差也限制在了1，把数据变换成分布于s函数的中间部分，这样就相当于我这一层网络所学习到的特征分布被你搞坏了。于是我们增加了变换重构，保留了网络所学习到的特征。

具体代码

  1. def batch_norm(is_training, X, gamma, beta, moving_mean, moving_var, eps, momentum):
  2.     # 判断当前模式是训练模式还是预测模式
  3.     if not is_training:
  4.         # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
  5.         X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
  6.     else:
  7.         assert len(X.shape) in (2, 4)
  8.         if len(X.shape) == 2:
  9.             # 使用全连接层的情况，计算特征维上的均值和方差
  10.             mean = X.mean(dim=0)
  11.             var = ((X - mean) ** 2).mean(dim=0)
  12.         else:
  13.             # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。这里我们需要保持
  14.             # X的形状以便后面可以做广播运算
  15.             mean = X.mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
  16.             var = ((X - mean) ** 2).mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
  17.         # 训练模式下用当前的均值和方差做标准化
  18.         X_hat = (X - mean) / torch.sqrt(var + eps)
  19.         # 更新移动平均的均值和方差
  20.         moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
  21.         moving_var = momentum * moving_var + (1.0 - momentum) * var
  22.     Y = gamma * X_hat + beta  # 拉伸和偏移
  23.     return Y, moving_mean, moving_var
  26. class BatchNorm(nn.Module):
  27.     def __init__(self, num_features, num_dims):
  28.         super(BatchNorm, self).__init__()
  29.         if num_dims == 2:
  30.             shape = (1, num_features)
  31.         else:
  32.             shape = (1, num_features, 1, 1)
  33.         # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成0和1
  34.         self.gamma = nn.Parameter(torch.ones(shape))
  35.         self.beta = nn.Parameter(torch.zeros(shape))
  36.         # 不参与求梯度和迭代的变量，全在内存上初始化成0
  37.         self.moving_mean = torch.zeros(shape)
  38.         self.moving_var = torch.zeros(shape)
  40.     def forward(self, X):
  41.         # 如果X不在内存上，将moving_mean和moving_var复制到X所在显存上
  42.         if self.moving_mean.device != X.device:
  43.             self.moving_mean = self.moving_mean.to(X.device)
  44.             self.moving_var = self.moving_var.to(X.device)
  45.         # 保存更新过的moving_mean和moving_var, Module实例的traning属性默认为true, 调用.eval()后设成false
  46.         Y, self.moving_mean, self.moving_var = batch_norm(self.training,
  47.             X, self.gamma, self.beta, self.moving_mean,
  48.             self.moving_var, eps=1e-5, momentum=0.9)
  49.         return Y
  51. net = nn.Sequential(
  52.             nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
  53.             BatchNorm(6, num_dims=4),
  54.             nn.Sigmoid(),
  55.             nn.MaxPool2d(2, 2), # kernel_size, stride
  56.             nn.Conv2d(6, 16, 5),
  57.             BatchNorm(16, num_dims=4),
  58.             nn.Sigmoid(),
  59.             nn.MaxPool2d(2, 2),
  60.             FlattenLayer(),
  61.             nn.Linear(16*4*4, 120),
  62.             BatchNorm(120, num_dims=2),
  63.             nn.Sigmoid(),
  64.             nn.Linear(120, 84),
  65.             BatchNorm(84, num_dims=2),
  66.             nn.Sigmoid(),
  67.             nn.Linear(84, 10)
  68.         )
  70. net = nn.Sequential(
  71.             nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
  72.             nn.BatchNorm2d(6),
  73.             nn.Sigmoid(),
  74.             nn.MaxPool2d(2, 2), # kernel_size, stride
  75.             nn.Conv2d(6, 16, 5),
  76.             nn.BatchNorm2d(16),
  77.             nn.Sigmoid(),
  78.             nn.MaxPool2d(2, 2),
  79.             FlattenLayer(),
  80.             nn.Linear(16*4*4, 120),
  81.             nn.BatchNorm1d(120),
  82.             nn.Sigmoid(),
  83.             nn.Linear(120, 84),
  84.             nn.BatchNorm1d(84),
  85.             nn.Sigmoid(),
  86.             nn.Linear(84, 10)
  87.         )
  88. """
  89. Net Struct as follows: 
  90. Sequential(
  91.   (0): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  92.   (1): BatchNorm2d(6, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  93.   (2): Sigmoid()
  94.   (3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  95.   (4): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  96.   (5): BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  97.   (6): Sigmoid()
  98.   (7): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  99.   (8): FlattenLayer()
  100.   (9): Linear(in_features=256, out_features=120, bias=True)
  101.   (10): BatchNorm1d(120, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  102.   (11): Sigmoid()
  103.   (12): Linear(in_features=120, out_features=84, bias=True)
  104.   (13): BatchNorm1d(84, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  105.   (14): Sigmoid()
  106.   (15): Linear(in_features=84, out_features=10, bias=True)
  107. )
  108. """

6. ResNet

残差网络是为了解决网络深度加深但是训练效果减弱的问题
优秀参考链接
https://zhuanlan.zhihu.com/p/42706477
原理大致如下图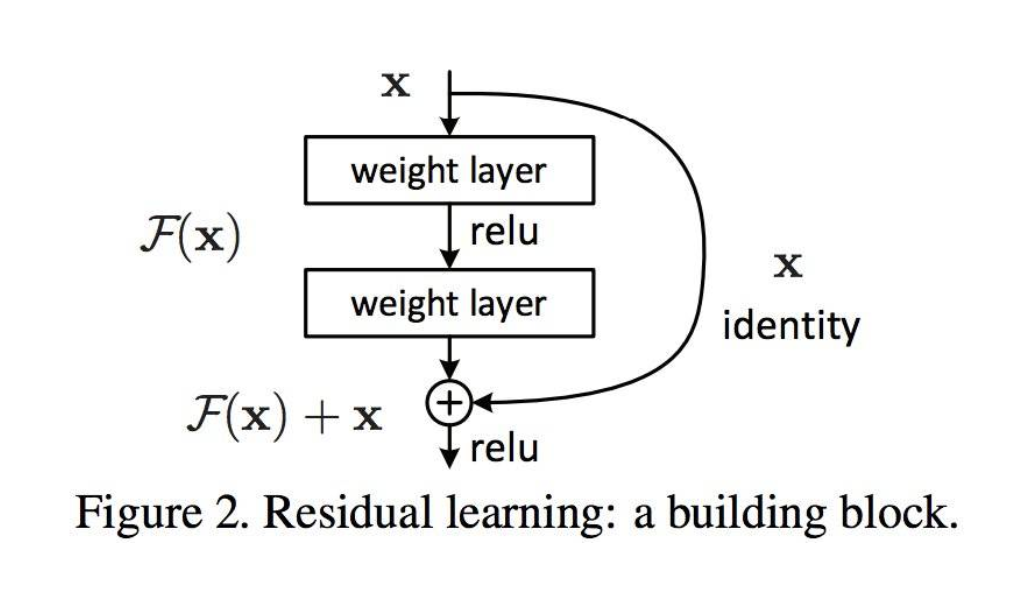
image.png
就是经过了卷积层的结果和原始数据进行结合，保证训练后的结果保留训练前的特征
换做实现就是经过两个卷积层的结果和原始输入相加再经过ReLu，其中如果经过卷积层有通道数的改变，那么在相加之前需要通过1*1的卷积层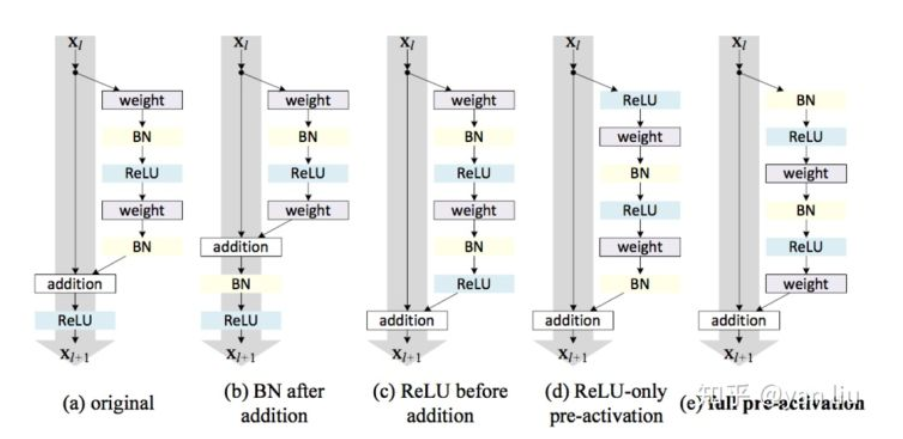
image.png

  1. class Residual(nn.Module):  # 本类已保存在d2lzh_pytorch包中方便以后使用
  2.     def __init__(self, in_channels, out_channels, use_1x1conv=False, stride=1):
  3.         super(Residual, self).__init__()
  4.         self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1, stride=stride)
  5.         self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
  6.         if use_1x1conv:
  7.             self.conv3 = nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride)
  8.         else:
  9.             self.conv3 = None
  10.         self.bn1 = nn.BatchNorm2d(out_channels)
  11.         self.bn2 = nn.BatchNorm2d(out_channels)
  13.     def forward(self, X):
  14.         Y = F.relu(self.bn1(self.conv1(X)))
  15.         Y = self.bn2(self.conv2(Y))
  16.         if self.conv3:
  17.             X = self.conv3(X)
  18.         return F.relu(Y + X)
  19.  net = nn.Sequential(
  20.         nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
  21.         nn.BatchNorm2d(64),
  22.         nn.ReLU(),
  23.         nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
  25. def resnet_block(in_channels, out_channels, num_residuals, first_block=False):
  26.     if first_block:
  27.         assert in_channels == out_channels # 第一个模块的通道数同输入通道数一致
  28.     blk = []
  29.     for i in range(num_residuals):
  30.         if i == 0 and not first_block:
  31.             blk.append(Residual(in_channels, out_channels, use_1x1conv=True, stride=2))
  32.         else:
  33.             blk.append(Residual(out_channels, out_channels))
  34.     return nn.Sequential(*blk)
  36. net.add_module("resnet_block1", resnet_block(64, 64, 2, first_block=True))
  37. net.add_module("resnet_block2", resnet_block(64, 128, 2))
  38. net.add_module("resnet_block3", resnet_block(128, 256, 2))
  39. net.add_module("resnet_block4", resnet_block(256, 512, 2))
  41. net.add_module("global_avg_pool", GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, 512, 1, 1)
  42. net.add_module("fc", nn.Sequential(FlattenLayer(), nn.Linear(512, 10)))
  43. """
  44. Net Struct as follows: 
  45. Sequential(
  46.   (0): Conv2d(1, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3))
  47.   (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  48.   (2): ReLU()
  49.   (3): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
  50.   (resnet_block1): Sequential(
  51.     (0): Residual(
  52.       (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  53.       (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  54.       (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  55.       (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  56.     )
  57.     (1): Residual(
  58.       (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  59.       (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  60.       (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  61.       (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  62.     )
  63.   )
  64.   (resnet_block2): Sequential(
  65.     (0): Residual(
  66.       (conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
  67.       (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  68.       (conv3): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2))
  69.       (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  70.       (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  71.     )
  72.     (1): Residual(
  73.       (conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  74.       (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  75.       (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  76.       (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  77.     )
  78.   )
  79.   (resnet_block3): Sequential(
  80.     (0): Residual(
  81.       (conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
  82.       (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  83.       (conv3): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2))
  84.       (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  85.       (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  86.     )
  87.     (1): Residual(
  88.       (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  89.       (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  90.       (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  91.       (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  92.     )
  93.   )
  94.   (resnet_block4): Sequential(
  95.     (0): Residual(
  96.       (conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
  97.       (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  98.       (conv3): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2))
  99.       (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  100.       (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  101.     )
  102.     (1): Residual(
  103.       (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  104.       (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  105.       (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  106.       (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  107.     )
  108.   )
  109.   (global_avg_pool): GlobalAvgPool2d()
  110.   (fc): Sequential(
  111.     (0): FlattenLayer()
  112.     (1): Linear(in_features=512, out_features=10, bias=True)
  113.   )
  114. )
  115. """

7. Dense_Net

稠密神经网络的和之前的一个不同点就是，他没有直接的合并两个数据源。而是把两个数据进行并联
所以数据在经过卷积层之后通道数会快速的增加，所以还有一个层是合并数据，减小计算量的

  1. def conv_block(in_channels, out_channels):
  2.     blk = nn.Sequential(nn.BatchNorm2d(in_channels),
  3.                         nn.ReLU(),
  4.                         nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
  5.     return blk
  6. #每一次的循环都会加大outchannel个通道
  7. class DenseBlock(nn.Module):
  8.     def __init__(self, num_convs, in_channels, out_channels):
  9.         super(DenseBlock, self).__init__()
  10.         net = []
  11.         for i in range(num_convs):
  12.             in_c = in_channels + i * out_channels
  13.             net.append(conv_block(in_c, out_channels))
  14.         self.net = nn.ModuleList(net)
  15.         self.out_channels = in_channels + num_convs * out_channels # 计算输出通道数
  17.     def forward(self, X):
  18.         for blk in self.net:
  19.             #print(blk)
  20.             Y = blk(X)
  21.             X = torch.cat((X, Y), dim=1)  # 在通道维上将输入和输出连结
  22.         return X
  23.  #这个模块是用于减小数据通道的，利用1*1的卷积以及2的步长减小通道和图片大小  
  24. def transition_block(in_channels, out_channels):
  25.     blk = nn.Sequential(
  26.             nn.BatchNorm2d(in_channels),
  27.             nn.ReLU(),
  28.             nn.Conv2d(in_channels, out_channels, kernel_size=1),
  29.             nn.AvgPool2d(kernel_size=2, stride=2))
  30.     return blk
  32. net = nn.Sequential(
  33.         nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
  34.         nn.BatchNorm2d(64),
  35.         nn.ReLU(),
  36.         nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
  39. num_channels, growth_rate = 64, 32  # num_channels为当前的通道数
  40. num_convs_in_dense_blocks = [4, 4, 4, 4]
  42. for i, num_convs in enumerate(num_convs_in_dense_blocks):
  43.     DB = DenseBlock(num_convs, num_channels, growth_rate)
  44.     net.add_module("DenseBlosk_%d" % i, DB)
  45.     # 上一个稠密块的输出通道数
  46.     num_channels = DB.out_channels
  47.     # 在稠密块之间加入通道数减半的过渡层
  48.     if i != len(num_convs_in_dense_blocks) - 1:
  49.         net.add_module("transition_block_%d" % i, transition_block(num_channels, num_channels // 2))
  50.         num_channels = num_channels // 2
  52. net.add_module("BN", nn.BatchNorm2d(num_channels))
  53. net.add_module("relu", nn.ReLU())
  54. net.add_module("global_avg_pool", GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, num_channels, 1, 1)
  55. net.add_module("fc", nn.Sequential(FlattenLayer(), nn.Linear(num_channels, 10)))
  58. '''
  59. Net Struct as follows: 
  60. Sequential(
  61.   (0): Conv2d(1, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3))
  62.   (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  63.   (2): ReLU()
  64.   (3): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
  65.   (DenseBlosk_0): DenseBlock(
  66.     (net): ModuleList(
  67.       (0): Sequential(
  68.         (0): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  69.         (1): ReLU()
  70.         (2): Conv2d(64, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  71.       )
  72.       (1): Sequential(
  73.         (0): BatchNorm2d(96, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  74.         (1): ReLU()
  75.         (2): Conv2d(96, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  76.       )
  77.       (2): Sequential(
  78.         (0): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  79.         (1): ReLU()
  80.         (2): Conv2d(128, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  81.       )
  82.       (3): Sequential(
  83.         (0): BatchNorm2d(160, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  84.         (1): ReLU()
  85.         (2): Conv2d(160, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  86.       )
  87.     )
  88.   )
  89.   (transition_block_0): Sequential(
  90.     (0): BatchNorm2d(192, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  91.     (1): ReLU()
  92.     (2): Conv2d(192, 96, kernel_size=(1, 1), stride=(1, 1))
  93.     (3): AvgPool2d(kernel_size=2, stride=2, padding=0)
  94.   )
  95.   (DenseBlosk_1): DenseBlock(
  96.     (net): ModuleList(
  97.       (0): Sequential(
  98.         (0): BatchNorm2d(96, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  99.         (1): ReLU()
  100.         (2): Conv2d(96, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  101.       )
  102.       (1): Sequential(
  103.         (0): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  104.         (1): ReLU()
  105.         (2): Conv2d(128, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  106.       )
  107.       (2): Sequential(
  108.         (0): BatchNorm2d(160, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  109.         (1): ReLU()
  110.         (2): Conv2d(160, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  111.       )
  112.       (3): Sequential(
  113.         (0): BatchNorm2d(192, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  114.         (1): ReLU()
  115.         (2): Conv2d(192, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  116.       )
  117.     )
  118.   )
  119.   (transition_block_1): Sequential(
  120.     (0): BatchNorm2d(224, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  121.     (1): ReLU()
  122.     (2): Conv2d(224, 112, kernel_size=(1, 1), stride=(1, 1))
  123.     (3): AvgPool2d(kernel_size=2, stride=2, padding=0)
  124.   )
  125.   (DenseBlosk_2): DenseBlock(
  126.     (net): ModuleList(
  127.       (0): Sequential(
  128.         (0): BatchNorm2d(112, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  129.         (1): ReLU()
  130.         (2): Conv2d(112, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  131.       )
  132.       (1): Sequential(
  133.         (0): BatchNorm2d(144, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  134.         (1): ReLU()
  135.         (2): Conv2d(144, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  136.       )
  137.       (2): Sequential(
  138.         (0): BatchNorm2d(176, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  139.         (1): ReLU()
  140.         (2): Conv2d(176, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  141.       )
  142.       (3): Sequential(
  143.         (0): BatchNorm2d(208, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  144.         (1): ReLU()
  145.         (2): Conv2d(208, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  146.       )
  147.     )
  148.   )
  149.   (transition_block_2): Sequential(
  150.     (0): BatchNorm2d(240, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  151.     (1): ReLU()
  152.     (2): Conv2d(240, 120, kernel_size=(1, 1), stride=(1, 1))
  153.     (3): AvgPool2d(kernel_size=2, stride=2, padding=0)
  154.   )
  155.   (DenseBlosk_3): DenseBlock(
  156.     (net): ModuleList(
  157.       (0): Sequential(
  158.         (0): BatchNorm2d(120, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  159.         (1): ReLU()
  160.         (2): Conv2d(120, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  161.       )
  162.       (1): Sequential(
  163.         (0): BatchNorm2d(152, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  164.         (1): ReLU()
  165.         (2): Conv2d(152, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  166.       )
  167.       (2): Sequential(
  168.         (0): BatchNorm2d(184, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  169.         (1): ReLU()
  170.         (2): Conv2d(184, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  171.       )
  172.       (3): Sequential(
  173.         (0): BatchNorm2d(216, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  174.         (1): ReLU()
  175.         (2): Conv2d(216, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  176.       )
  177.     )
  178.   )
  179.   (BN): BatchNorm2d(248, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  180.   (relu): ReLU()
  181.   (global_avg_pool): GlobalAvgPool2d()
  182.   (fc): Sequential(
  183.     (0): FlattenLayer()
  184.     (1): Linear(in_features=248, out_features=10, bias=True)
  185.   )
  186. )
  187. '''