数学建模刚好有的有用到，于是手写代码实现一下

题目

设某仓库前有一卸货场，货车一般是夜间到达，白天卸货，每天只能卸货 2 车，若一天内到达数超过 2 车，那么就推迟到次日卸货。根据表 3 所示的数据，货车到 达数的概率分布（相对频率）平均为 1.5 车/天，求每天推迟卸货的平均车数。

解: 这是单服务台的排队系统，可验证到达车数不服从泊松分布，服务时间也不服从指数分布（这是定长服务时间）。随机模拟法首先要求事件能按历史的概率分布规律出现。模拟时产生的随机数与事件的对应关系如表4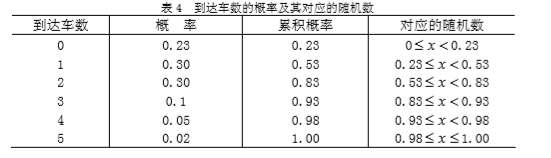

解答

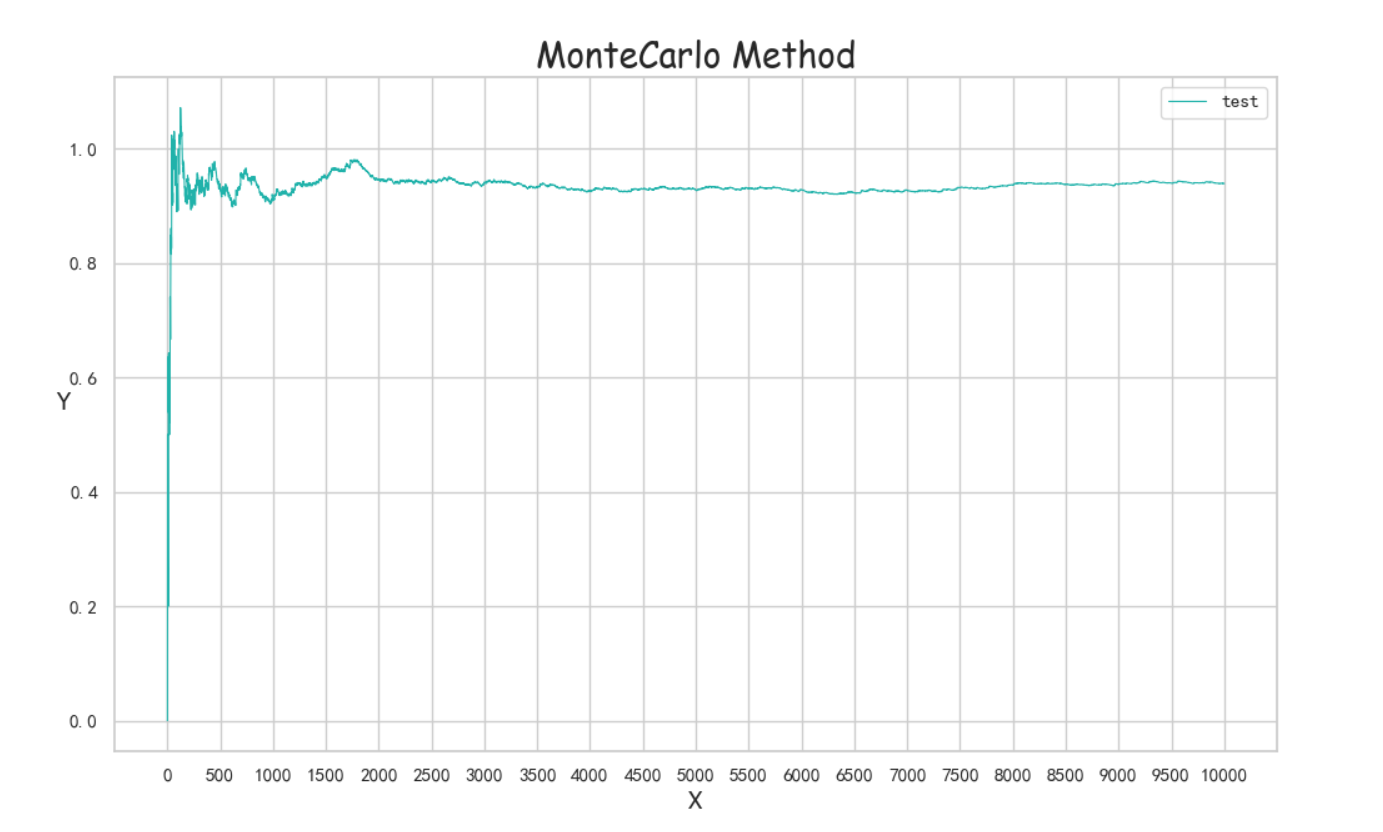
import random
prob=[0.23,0.3,0.3,0.1,0.05,0.02]
def possess_prob(prob):
    temp=0
    new_prob=[]
    for i in prob:
        temp+=i
        new_prob.append(temp)
    print(new_prob)
    return new_prob
def once(prob1,day):
    wait=0
    cur_wait=0
    for i in range(day):
        temp = random.random()
        index = 0
        for i in prob1:
            if temp < i:
                break
            index += 1
        cur_wait+=index
        if cur_wait>=2:
            cur_wait-=2
        else:
            cur_wait=0
        if cur_wait>0:
            wait+=cur_wait
    return cur_wait
from Draw import Draw
def run(times,day):
    print("----start----")
    prob1=possess_prob(prob)
    result=[]
    sum=0
    for i in range(times):
        temp=once(prob1,day)
        sum+=temp
        lens=len(result)+1
        result.append(sum/lens)
    Draw([result], ["test"], range(len(result)), "MonteCarlo Method")
run(10000,100)