语言模型

语言模型用于描述语言，通常认为一个词的前面的若干词和他是有关联的，所以训练的数据和目的就是围绕着一段词语展开的，n元就是这个词和前面n-1个词构成的数据

循环神经网络

训练数据

循环神经网络的训练就是使用上面所说的一个词条作为训练的数据输入
具体输入的数据是使用one_hot编码的，也就是一个很长很稀疏的矩阵

网络结构

循环神经网络通常是当前的数据输入乘上参数1，再加上上一次的隐藏状态乘上参数2，最后加上偏置三个部分构成。
最后这个整体还需要放入全连接层和激活函数进行计算，上述的三个部分之后就认为是隐藏状态，也正是下一次计算的数据成分，所以可以看作是一个循环的过程。因此称为是循环神经网络。

参数

这个循环神经网络有一个超参数就是循环的时间步，也就是多少个词拼在一起作为循环的输入。还有一个就是隐藏层的维数，上述的参数1和参数2都是（T*W）的（T是时间步，W是隐藏层的维数）

数据投喂

对于这样的一个循环神经网络，数据的输入就是来自于文本，文本切割成为一份份数据。有两种数据的投喂的方法，一种就是连续的方法，一篇文章切割好了之后就按照顺序把数据投喂，这种的方法可以保证了隐藏状态不用清空，但是需要使用detach剥离出计算图，防止梯度计算过于复杂。另一种就是随机的从切割好的块里随便拿，文本就是不连续的，所以需要在新的一份数据进入之前重置隐藏状态。

RNN实现

代码（复杂实现）（同样的，代码来自原教程）
  1. def get_params():
  2.     def _one(shape):
  3.         ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
  4.         return torch.nn.Parameter(ts, requires_grad=True)
  6.     #这里的就是参数1和参数2，两个参数矩阵
  7.     # 隐藏层参数
  8.     W_xh = _one((num_inputs, num_hiddens))
  9.     W_hh = _one((num_hiddens, num_hiddens))
  10.     b_h = torch.nn.Parameter(torch.zeros(num_hiddens, device=device, requires_grad=True))
  11.     # 输出层参数
  12.     W_hq = _one((num_hiddens, num_outputs))
  13.     b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, requires_grad=True))
  14.     return nn.ParameterList([W_xh, W_hh, b_h, W_hq, b_q])
  16. def init_rnn_state(batch_size, num_hiddens, device):
  17.     return (torch.zeros((batch_size, num_hiddens), device=device), )
  20. def rnn(inputs, state, params):
  21.     # inputs和outputs皆为num_steps个形状为(batch_size, vocab_size)的矩阵
  22.     W_xh, W_hh, b_h, W_hq, b_q = params
  23.     H, = state
  24.     outputs = []
  25.     for X in inputs:
  26.         H = torch.tanh(torch.matmul(X, W_xh) + torch.matmul(H, W_hh) + b_h)
  27.         Y = torch.matmul(H, W_hq) + b_q
  28.         outputs.append(Y)
  29.     return outputs, (H,)

然后由于这个网络的特性所以需要引入两个概念，一个是裁剪梯度，一个是困惑度

裁剪梯度

裁剪梯度就是为了避免梯度的过度生长
循环神经网络中较容易出现梯度衰减或梯度爆炸。为了应对梯度爆炸，我们可以裁剪梯度（clip gradient）。假设我们把所有模型参数梯度的元素拼接成一个向量，计算向量的模长x，然后设定一个参数a，min（a/x，1）* 梯度。

困惑度

困惑度可以理解是

  • 最佳情况下，模型总是把标签类别的概率预测为1，此时困惑度为1；
  • 最坏情况下，模型总是把标签类别的概率预测为0，此时困惑度为正无穷；
  • 基线情况下，模型总是预测所有类别的概率都相同，此时困惑度为类别个数。

PS：中间还有一节是介绍按照时间计算梯度方向传播的，同时解释了为什么梯度会有衰减和爆炸，但是很遗憾，看不懂。。。看的头大

GRU实现

网络结构

网络结构和计算方法和之前不一样的就是多了两个选择的参数，重置门和更新门。还多了一个变量：候选隐藏参数
更新门（R)：决定当前状态的计算值和候选隐藏参数在最后的结果中所占的比例
重置门（Z）：他负责决定是否重置候选隐藏状态

二者的计算公式和全连接层是一样，也就是二者各自都有了2个参数矩阵和一个偏置矩阵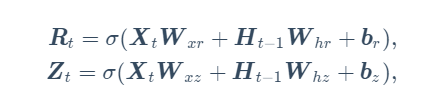
image.png
H就是上一个隐藏状态，x是最新的一次的数据输入，在乘法和加法结束之后进入sigmoid保证数据在【0，1】

然后讨论如何计算得到的隐藏状态（整体的计算流程图如下，有*符号的是矩阵乘法，没有的就是按元素乘

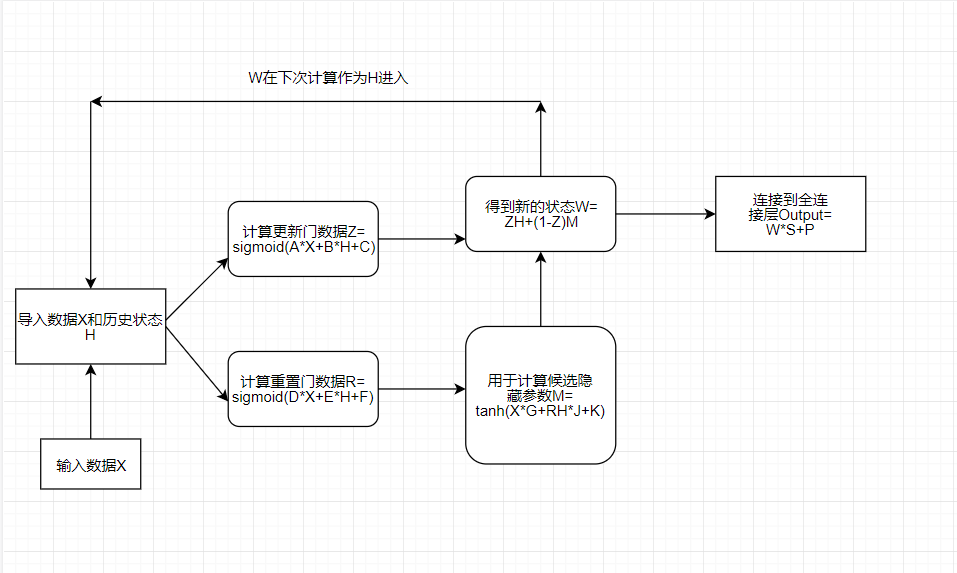
image.png
重置门的参数按元素乘到候选隐藏参数，可以看作是对这个数据的调整，比如重置门为0的元素会把对应位置的候选隐藏参数的元素清零

  1. def get_params():
  2.     def _one(shape):
  3.         ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
  4.         return torch.nn.Parameter(ts, requires_grad=True)
  5.     def _three():
  6.         return (_one((num_inputs, num_hiddens)),
  7.                 _one((num_hiddens, num_hiddens)),
  8.                 torch.nn.Parameter(torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True))
  10.     W_xz, W_hz, b_z = _three()  # 更新门参数
  11.     W_xr, W_hr, b_r = _three()  # 重置门参数
  12.     W_xh, W_hh, b_h = _three()  # 候选隐藏状态参数
  14.     # 输出层参数
  15.     W_hq = _one((num_hiddens, num_outputs))
  16.     b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, dtype=torch.float32), requires_grad=True)
  17.     return nn.ParameterList([W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q])
  20. def init_gru_state(batch_size, num_hiddens, device):
  21.     return (torch.zeros((batch_size, num_hiddens), device=device), )
  24. def gru(inputs, state, params):
  25.     W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
  26.     H, = state
  27.     outputs = []
  28.     for X in inputs:#注意到这里两种矩阵的运算，matmul和*
  29.         Z = torch.sigmoid(torch.matmul(X, W_xz) + torch.matmul(H, W_hz) + b_z)
  30.         R = torch.sigmoid(torch.matmul(X, W_xr) + torch.matmul(H, W_hr) + b_r)
  31.         H_tilda = torch.tanh(torch.matmul(X, W_xh) + torch.matmul(R * H, W_hh) + b_h)
  32.         H = Z * H + (1 - Z) * H_tilda
  33.         Y = torch.matmul(H, W_hq) + b_q
  34.         outputs.append(Y)
  35.     return outputs, (H,)

LSTM实现

网络架构
  1.               ![](https://cdn.nlark.com/yuque/0/2020/svg/296244/1581252319103-27f19988-8991-4e6e-b559-65d577a40230.svg#align=left&display=inline&height=276&originHeight=276&originWidth=508&size=0&status=done&style=none&width=508)

这里的网络多出了记忆细胞等东西
和前面类似的遗忘门，输入门，输出门的计算都是全连接层的那种

  1. def get_params():
  2.     def _one(shape):
  3.         ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
  4.         return torch.nn.Parameter(ts, requires_grad=True)
  5.     def _three():
  6.         return (_one((num_inputs, num_hiddens)),
  7.                 _one((num_hiddens, num_hiddens)),
  8.                 torch.nn.Parameter(torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True))
  10.     W_xi, W_hi, b_i = _three()  # 输入门参数
  11.     W_xf, W_hf, b_f = _three()  # 遗忘门参数
  12.     W_xo, W_ho, b_o = _three()  # 输出门参数
  13.     W_xc, W_hc, b_c = _three()  # 候选记忆细胞参数
  15.     # 输出层参数
  16.     W_hq = _one((num_hiddens, num_outputs))
  17.     b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, dtype=torch.float32), requires_grad=True)
  18.     return nn.ParameterList([W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q])
  21. def init_lstm_state(batch_size, num_hiddens, device):
  22.     return (torch.zeros((batch_size, num_hiddens), device=device),
  23.             torch.zeros((batch_size, num_hiddens), device=device))
  25. def lstm(inputs, state, params):
  26.     [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q] = params
  27.     (H, C) = state
  28.     outputs = []
  29.     for X in inputs:
  30.         I = torch.sigmoid(torch.matmul(X, W_xi) + torch.matmul(H, W_hi) + b_i)
  31.         F = torch.sigmoid(torch.matmul(X, W_xf) + torch.matmul(H, W_hf) + b_f)
  32.         O = torch.sigmoid(torch.matmul(X, W_xo) + torch.matmul(H, W_ho) + b_o)
  33.         C_tilda = torch.tanh(torch.matmul(X, W_xc) + torch.matmul(H, W_hc) + b_c)
  34.         C = F * C + I * C_tilda
  35.         H = O * C.tanh()
  36.         Y = torch.matmul(H, W_hq) + b_q
  37.         outputs.append(Y)
  38.     return outputs, (H, C)

深度循环神经网络

原来的RNN只是有一层的隐藏层，和先前MLP的区别就是会把上次的状态再输入
深度RNN的隐藏层不止一层，输出的H会作为和X类似的输入再进入下一层（第一层的输入是X，第二层是第一层的H，就是这个区别，每一层都有独立的一份参数）

双向循环神经网络

前面的循环网络都是把前面的状态输入到后面的运算里，双向顾名思义就是把后面的也作为输入输入到前面的网络层中进行计算