二叉搜索树/平衡二叉树

二叉搜索树/平衡二叉树

1、二叉搜索树(BST)的定义

二叉搜索树是一种基于节点的二叉树数据结构，具有以下属性:

• 节点的左子树只包含键值小于节点键值的节点。
• 节点的右子树只包含键大于该节点键的节点。
• 左右子树也必须是二叉搜索树。

• 不能有重复的节点。

  2、插入

  简单插入：
  从根开始搜索一个键，直到找到一个叶节点。一旦找到一个叶节点，新节点将作为叶节点的子节点添加。
  比较插入：

• 从根开始。

• 将插入元素与根元素进行比较，如果小于根元素，则递归向左，否则递归向右。

• 到达末尾后，只需在左边(如果小于当前节点)插入该节点，否则在右边插入该节点。

  3、删除

  删除有以下几种情况：

• 删除的结点是叶结点，直接从树中删除

• 删除的结点有一个叶结点；将叶结点复制到结点并删除叶结点
• 删除的结点有两个叶结点：具体有两种方式（中序遍历）：
  • 将当前结点的右结点的左子树的最小值复制到当前结点，并删除最小值结点
  • 将当前结点的左结点的右子树的最大值复制到当前结点，并删除最大值结点

注意：中序遍历的结果是从小到大。

4、平衡二叉树

一棵空树是平衡二叉树；若 T 是一棵非空二叉树，其左、右子树为和，令和分别为左、右子树的深度。当且仅当：

• 和都是平衡二叉树；
• -≤ 1；

时，则 T 是平衡二叉树。
相应地定义-为二叉平衡树的平衡因子 (balance factor) 。因此，平衡二叉树上所有结点的平衡因子可能是 -1 ， 0 ， 1 。
换言之，若一棵二叉树上任一结点的平衡因子的绝对值都不大于 1 ，则该树是就平衡二叉树。
为什么有平衡二叉树？
二叉树的理想时间复杂度是，最坏情况是。如下图所示：

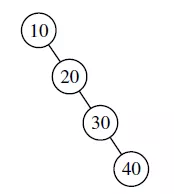
重平衡二叉搜索树的主要操作称为旋转。
假设存在x、y和z的三叉树重组(对应于单或双旋转)后的树T ，从左到右的叶子结点分别为，存在以下几种情况：

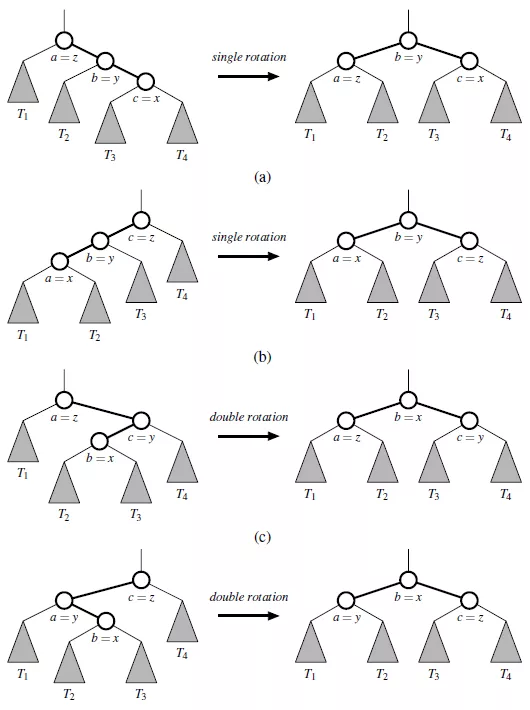
5、实现

LinkedBinaryTree、 MapBase

import LinkedBinaryTree, MapBase
class TreeMap(LinkedBinaryTree, MapBase):
    """sorted map implementation using a binary search tree"""
    # ---------------override position class-------------
    class Position(LinkedBinaryTree.Position):
        def key(self):
            """return key of map's key-value pair"""
            return self.element()._key
        def value(self):
            return self.element()._value
    # --------------------- nonpublic utilities ------------------
    def _subtree_search(self, p, k):
        """return Position of p's subtree having key k, or last node searched"""
        if k == p.key():
            return p
        elif k < p.key():
            if self.left(p) is not None:
                return self._subtree_search(self.left(p), k)
            elif self.right(p) is not None:
                return self._subtree_search(self.right(p), k)
        return p
    def _subtree_first_position(self, p):
        """return position of first item in subtree rooted at p."""
        walk = p
        while self.left(walk) is not None:  # keep walking left
            walk = self.left(walk)
        return walk
    def _subtree_last_position(self, p):
        """return position of last item in subtree rooted at p"""
        walk = p
        while self.right(walk) is not None:
            walk = self.right(walk)
        return walk
    def first(self):
        """return the first postion in the tree, 最小值 """
        return self._subtree_first_position(self.root()) if len(self) > 0 else None
    def last(self):
        """return the last position in the tree, 最大值"""
        return self._subtree_last_position(self.root()) if len(self) > 0 else None
    def before(self, p):
        """
        return the position just before p in the natural order.
        return None if p is the first position.
        """
        self._validate(p)  # inherited from LinkedBinaryTree
        if self.left(p):
            # 查找p结点左子树的最大值
            return self._subtree_last_position(self.left(p))
        else:
            # 如果p结点没有左子树，则找其父节点
            # walk upward
            walk = p
            above = self.parent(walk)
            while above is not None and walk == self.left(above):
                walk = above
                above = self.parent(walk)
            return above
    def after(self, p):
        """
        return the position just after p in the natural order.
        return None if p is the last position.
        """
        self._validate(p)  # inherited from LinkedBinaryTree
        if self.right(p):
            return self._subtree_first_position(self.right(p))
        else:
            # walk upward
            walk = p
            above = self.parent(walk)
            while above is not None and walk == self.right(above):
                walk = above
                above = self.parent(walk)
            return above
    def find_position(self, k):
        """return position with key k, or else neighbor """
        if self.is_empty():
            return None
        else:
            p = self._subtree_search(self.root(), k)
            self._rebalance_access(p)  # hook for balanced tree subclasses
            return p
    def find_min(self):
        """return (key,value) pair with minimum key"""
        if self.is_empty():
            return None
        else:
            p = self.first()
            return (p.key(), p.value())
    def find_ge(self, k):
        """
        return (key,value) pair with least key greater than or equal to k.
        return None if there does not exist such a key
        """
        if self.is_empty():
            return None
        else:
            p = self.find_position(k)
            if p.key() < k:  # may not find exact match
                p = self.after(p)  # p’s key is too small
            return (p.key(), p.value()) if p is not None else None
    def find_range(self, start, stop):
        """iterate all (key,value) pairs such that start<=key<stop.
        if start is None, iteration begins with minimum key of map.
        if stop is None,iteration continues through the maximum key of map"""
        if not self.is_empty():
            if start is None:
                p = self.first()
            else:
                # initialize p with logic similar to find_ge
                p = self.find_position(start)
                if p.key() < start:
                    p = self.after(p)
            while p is not None and (stop is None or p.key() < stop):
                yield (p.key(), p.value())
                p = self.after(p)
    def __getitem__(self, k):
        """return value associated with key k (raise KeyError if not found)"""
        if self.is_empty():
            raise KeyError('Key Error: ' + repr(k))
        else:
            p = self._subtree_search(self.root(), k)
            self._rebalance_access(p)  # hook for balanced tree subclasses
            if k != p.key():
                raise KeyError('Key Error: ' + repr(k))
            return p.value()
    def __setitem__(self, k, v):
        """assign value v to key k, overwriting existing value if present"""
        if self.is_empty():
            leaf = self._add_root(self._Item(k, v))  # from LinkedBinaryTree
        else:
            p = self._subtree_search(self.root(), k)
            if p.key() == k:
                p.element()._value = v  # replace existing item's value
                self._rebalance_access(p)  # hook for balanced tree subclasses
                return
            else:
                item = self._Item(k, v)
                if p.key() < k:
                    leaf = self._add_right(p, item)  # inherited from LinkedBinaryTree
                else:
                    leaf = self._add_left(p, item)  # inherited from LinkedBinaryTree
        self._rebalance_insert(leaf)  # hook for balanced tree subclasses
    def __iter__(self):
        """generate an iteration of all keys in the map in order"""
        p = self.first()
        while p is not None:
            yield p.key()
            p = self.after(p)
    def delete(self, p):
        """remove the item at given position"""
        self._validate(p)
        if self.left(p) and self.right(p):
            replacement = self._subtree_last_position(self.left(p))
            self._replace(p, replacement.element())
            p = replacement
        # now p has at most one child
        parent = self.parent(p)
        self._delete(p)
        self._rebalance_delete(parent)  # if root deleted, parent is None
    def __delitem__(self, k):
        """remove the item at given position"""
        if not self.is_empty():
            p = self._subtree_search(self.root(), k)
            if k == p.ley():
                self.delete(p)  # rely on positional version
                return
            self._rebalance_access(p)  # hook for balanced tree subclasses
        raise KeyError('KeyError: ' + repr(k))
    def _rebalance_insert(self, p):
        pass
    def _rebalance_delete(self, p):
        pass
    def _rebalance_access(self, p):
        pass
    def _relink(self, parent, child, make_left_child):
        """relink parent node with child node (we allow child to be None)"""
        if make_left_child:
            parent._left = child
        else:
            parent._right = child
        if child is not None:
            child._parent = parent
    def _rotate(self, p):
        """rotate position p above its parent"""
        # z-->y-->x
        x = p._node
        y = x._parent  # we assume this exists
        z = y._parent  # grandparent (possibly None)
        if z is None:
            self._root = x  # x becomes root
            x._parent = None
        else:
            self._relink(z, x, y == z._left)  # x becomes a direct child of z
        # Now rotate x and y , including transfer of middle subtree
        if x == y._left:
            self._relink(y, x._right, True)  # x. right becomes left child of y
            self._relink(x, y, False)  # y becomes right child of x
        else:
            self._relink(y, x._left, False)  # x. left becomes right child of y
            self._relink(x, y, True)  # y becomes left child of x
    def _restructure(self, x):
        """perform trinode restructure of position x with parent/grandparent"""
        y = self.parent(x)
        z = self.parent(y)
        if (x == self.right(y)) == (y == self.right(z)):  # matching alignments
            self._rotate(y)  # single rotation (of y)
            return y  # y is new subtree root
        else:  # opposite alignments
            self._rotate(x)  # double rotation (of x)
            self._rotate(x)
            return x  # x is new subtree root
if __name__ == '__main__':
    #--------------------
    T = TreeMap()
    T['b'] = 4
    T['a'] = 5
    T['c'] = 6
    p = T.first()
    print(p.key())
    print(T.parent(p).key())
    print(T.find_position('a').value(),
          T.find_position('b').value(),
          T.find_position('c').value())
    last = T.last()
    print(T.left(p),T.right(p))
    print(last.key())
    print([*T])
    print(T['a'])
    T.delete(p)
    print([*T])