霍夫曼编码

数据结构 霍夫曼编码
霍夫曼编码（Huffman Coding），一种用于无损数据压缩的熵编码算法，由美国计算机科学家大卫·霍夫曼在 1952 年提出。
霍夫曼编码，除用于 GZIP、BZIP2、PKZIP 这些常规的压缩格式中，它通常还用于压缩重复率比较高的字符数据。
字符重复的频率越高，霍夫曼编码的工作效率就越高！
假设下面的字符串要通过网络发送。

每个字符占 8 个比特，上面这串字符总共有 15 个字符，所以一共要占用 15*8=120 个比特。
如果使用霍夫曼编码的话，就可以将这串字符压缩到一个更小的尺寸。怎么做到的呢？
霍夫曼编码首先会使用字符的频率创建一棵树，然后通过这个树的结构为每个字符生成一个特定的编码，出现频率高的字符使用较短的编码，出现频率低的则使用较长的编码，这样就会使编码之后的字符串平均长度降低，从而达到数据无损压缩的目的。
拿上面这串初始字符来一步步的说明下霍夫曼编码的工作步骤。
第一步，计算字符串中每个字符的频率。

B 出现 1 次，C 出现 6 次，A 出现 5 次，D 出现 3 次。
第二步，按照字符出现的频率进行排序，组成一个队列 Q。

出现频率最低的在前面，出现频率高的在后面。
第三步，把这些字符作为叶子节点开始构建一颗树。首先创建一个空节点 z，将最小频率的字符分配给 z 的左侧，并将频率排在第二位的分配给 z 的右侧，然后将 z 赋值为两个字符频率的和。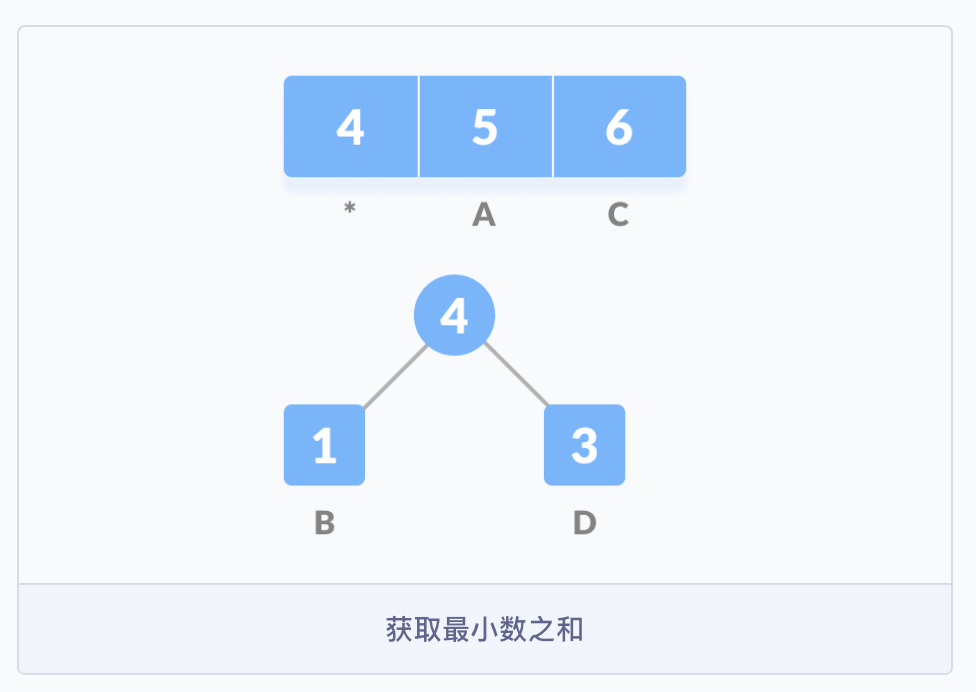

B 的频率最小，所以在左侧，然后是频率为 3 的 D，在右侧；然后把它们的父节点的值设为 4，子节点的频率之和。
然后从队列 Q 中删除 B 和 D，并将它们的和添加到队列中，上图中 * 表示的位置。紧接着，重新创建一个空的节点 z，并将 4 作为左侧的节点，频率为 5 的 A 作为右侧的节点，4 与 5 的和作为父节点。

继续按照之前的思路构建树，直到所有的字符都出现在树的节点中。

第四步，对于每个非叶子节点，将 0 分配给连接线的左侧，1 分配给连接线的右侧。此时，霍夫曼树就构建完成了。霍夫曼树又称为最优二叉树，是一种带权路径长度最短的二叉树。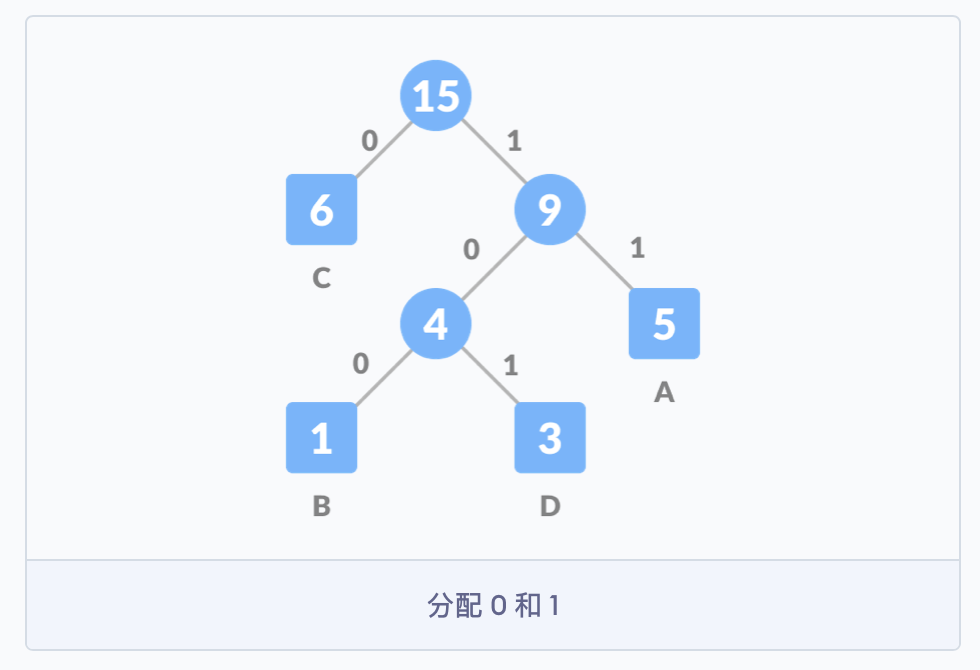

当树构建完毕后，来统计一下要发送的比特数。

1）来看字符这一列。四个字符 A、B、C、D 共计 4*8=32 比特。每个英文字母均占用一个字节，即 8 个比特。
2）来看频率这一列。A 5 次，B 1 次，C 6 次，D 3 次，一共 15 比特。
3）来看编码这一列。A 的编码为 11，对应霍夫曼树上的 15→9→5，也就是说，从根节点走到叶子节点 A，需要经过 11 这条路径；对应的 B 需要走过 100 这条路径；对应的 D 需要走过 101 这条路径；对应的 C 需要走过 0 这条路径。
4）来看长度这一列。A 的编码为 11，出现了 5 次，因此占用 10 个比特，即 1111111111；B 的编码为 100，出现了 1 次，因此占用 3 个比特，即 100；C 的编码为 0，出现了 6 次，因此占用 6 个比特，即 000000；D 的编码为 101，出现了 3 次，因此占用 9 个比特，即 101101101。
哈夫曼编码从本质上讲，是将最宝贵的资源（最短的编码）给出现概率最多的数据。在上面的例子中，C 出现的频率最高，它的编码为 0，就省下了不少空间。
在没有经过霍夫曼编码之前，字符串“BCAADDDCCACACAC”的二进制为：
10000100100001101000001010000010100010001000100010001000100001101000011010000010100001101000001010000110100000101000011
也就是占了 120 比特。
编码之后为：
0000001001011011011111111111
占了 28 比特。
但考虑到解码，需要把霍夫曼树的结构也传递过去，于是字符占用的 32 比特和频率占用的 15 比特也需要传递过去。总体上，编码后比特数为 32 + 15 + 28 = 75，比 120 比特少了 45 个，效率还是非常高的。
关于霍夫曼编码的 Java 示例。

class HuffmanNode {
    int item;
    char c;
    HuffmanNode left;
    HuffmanNode right;
}
class ImplementComparator implements Comparator<HuffmanNode> {
    public int compare(HuffmanNode x, HuffmanNode y) {
        return x.item - y.item;
    }
}
public class Huffman {
    public static void printCode(HuffmanNode root, String s) {
        if (root.left == null && root.right == null && Character.isLetter(root.c)) {
            System.out.println(root.c + "   |  " + s);
            return;
        }
        printCode(root.left, s + "0");
        printCode(root.right, s + "1");
    }
    public static void main(String[] args) {
        int n = 4;
        char[] charArray = { 'A', 'B', 'C', 'D' };
        int[] charfreq = { 5, 1, 6, 3 };
        PriorityQueue<HuffmanNode> q = new PriorityQueue<HuffmanNode>(n, new ImplementComparator());
        for (int i = 0; i < n; i++) {
            HuffmanNode hn = new HuffmanNode();
            hn.c = charArray[i];
            hn.item = charfreq[i];
            hn.left = null;
            hn.right = null;
            q.add(hn);
        }
        HuffmanNode root = null;
        while (q.size() > 1) {
            HuffmanNode x = q.peek();
            q.poll();
            HuffmanNode y = q.peek();
            q.poll();
            HuffmanNode f = new HuffmanNode();
            f.item = x.item + y.item;
            f.c = '-';
            f.left = x;
            f.right = y;
            root = f;
            q.add(f);
        }
        System.out.println(" 字符 | 霍夫曼编码 ");
        System.out.println("--------------------");
        printCode(root, "");
    }
}

本例的输出结果如下所示：

字符 | 霍夫曼编码 
--------------------
C   |  0
B   |  100
D   |  101
A   |  11