树

1、树简介

树是一种非线性结构。比数组和链表快。
树不是顺序排列的对象之间简单的前后关系，而是分层的，有些对象在上面，有些对象在下面。
树是一种抽象的数据类型，它分层次地存储元素。除了顶部元素外，树中的每个元素都有一个父元素和零个或多个子元素。
一棵树通常是通过在椭圆或矩形中放置元素，并通过直线画出父母和孩子之间的连接来实现的。
通常称顶部元素为树的根，但它被绘制为最高的元素，其他元素被连接在下面(与植物树相反)。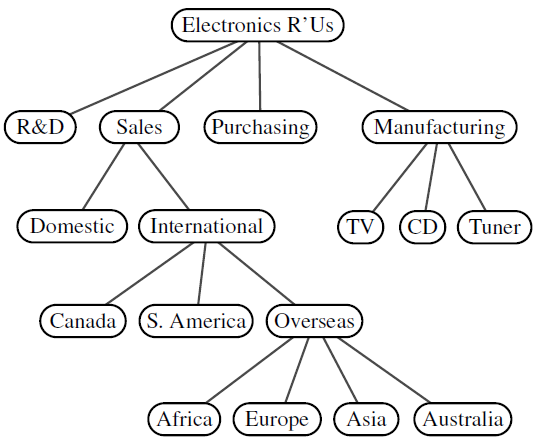
2021-08-26-21-14-20-508423.png
设p是t树的一个节点的位置，p的深度是p的祖先的个数，不包括p本身。
p的深度也可以递归定义为：

  • 如果p是根，则p的深度为0。
  • 否则，p的深度等于1加上p的父结点的深度。

树T中位置p的高度也是递归定义的：

  • 如果p是叶节点，那么p的高度是0。
  • 否则，p的高度比p子结点的最大高度大1。

代码如下：

  1. class Tree:
  2.     """abstract base class representing a tree structure"""
  4.     # ----------------------nested Position class----------------
  5.     class Position:
  6.         """an abstraction reprenting the location of a single element"""
  8.         def element(self):
  9.             """return the element stored at this Position"""
  10.             raise NotImplementedError('must be implemented by subclass')
  12.         def __eq__(self, other):
  13.             """return true if other Position represents the same location"""
  14.             raise NotImplementedError('must be implemented by subclass')
  16.         def __ne__(self, other):
  17.             return not (self == other)
  19.     # --------------abstract methods that concrete subclass must support------
  20.     def root(self):
  21.         """return position representing the tree's root (None if empty)"""
  22.         raise NotImplementedError('must be implemented by subclass')
  24.     def parent(self, p):
  25.         """Return Position representing p s parent (or None if p is root)"""
  26.         raise NotImplementedError('must be implemented by subclass')
  28.     def num_children(self, p):
  29.         """Return the number of children that Position p has"""
  30.         raise NotImplementedError('must be implemented by subclass')
  32.     def children(self, p):
  33.         """Generate an iteration of Positions representing p s children"""
  34.         raise NotImplementedError('must be implemented by subclass')
  36.     def __len__(self):
  37.         """Return the total number of elements in the tree"""
  38.         raise NotImplementedError('must be implemented by subclass')
  40.     # ---------- concrete methods implemented in this class ----------
  41.     def is_root(self, p):
  42.         return self.root() == p
  44.     def is_leaf(self, p):
  45.         return self.num_children(p) == 0
  47.     def is_empty(self):
  48.         return len(self) == 0
  50.     def depth(self, p):
  51.         """Return the number of levels separating Position p from the root."""
  52.         if self.is_root(p):
  53.             return 0
  54.         else:
  55.             return self.depth(self.parent(p)) + 1
  57.     def _height1(self):
  58.         """return the height of the tree"""
  59.         return max(self.depth(p) for p in self.positions() if self.is_leaf(p))
  61.     def _height2(self, p):
  62.         """return the height of the subtree rooted at position p"""
  63.         if self.is_leaf(p):
  64.             return 0
  65.         else:
  66.             return max(self._height2(c) for c in self.children(p)) + 1
  68.     def height(self, p=None):
  69.         """
  70.         return the height of the subtree rooted at postion p.
  71.         if p is None, return the height of the entire tree
  72.         """
  73.         if p is None:
  74.             p = self.root()
  75.         return self._height2(p)

2、二叉树

二叉树是一种有序树，具有以下属性：

  • 每个节点最多有两个子节点。
  • 每个子节点都被标记为左子节点或右子节点。
  • 节点顺序，左子节点在右子节点之前

代码如下：

  1. class BinaryTree(Tree):
  2.     """abstract base class representing a binary tree structure"""
  4.     # --------------additional abstract methods------------
  5.     def left(self, p):
  6.         """return a position representing p's left child. """
  7.         raise NotImplementedError('must be implemented by subclass')
  9.     def right(self, p):
  10.         """return a position representing p's right child"""
  11.         raise NotImplementedError('must be implemented by subclass')
  13.     # -------concrete methods implemented in this class--------
  14.     def sibling(self, p):
  15.         """return a position representing p's sibling """
  16.         parent = self.parent(p)
  17.         if parent is None:
  18.             return None
  19.         else:
  20.             if p == self.left(parent):
  21.                 return self.right(parent)
  22.             else:
  23.                 return self.left(parent)
  25.     def children(self, p):
  26.         """generate an iteration of positions representing p's children"""
  27.         if self.left(p) is not None:
  28.             yield self.left(p)
  29.         if self.right(p) is not None:
  30.             yield self.right(p)

3、链表树

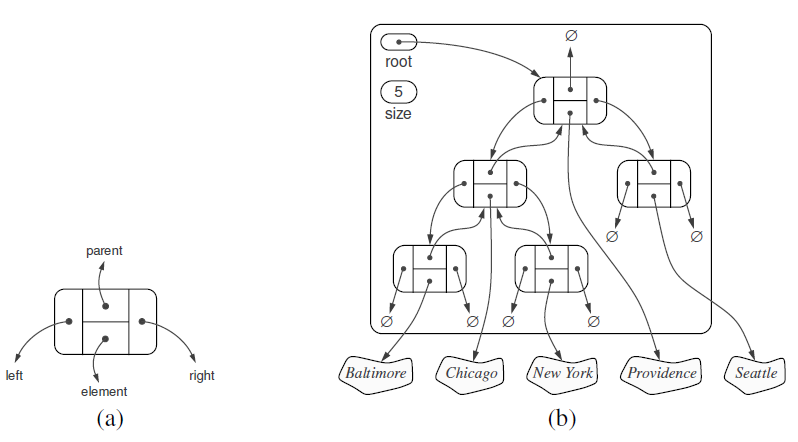
2021-08-26-21-14-20-677420.png
代码如下：
LinkedQueue

import LinkedQueue
class LinkedBinaryTree(BinaryTree):
    """Linked representation of a binary tree structure"""

    class _Node:
        """lightweight , nonpublic class for storing a node"""
        __slots__ = '_element', '_parent', '_left', '_right'

        def __init__(self, element, parent=None, left=None, right=None):
            self._element = element
            self._parent = parent
            self._left = left
            self._right = right

    class Position(BinaryTree.Position):
        """an abstraction representing the location of a single element"""

        def __init__(self, container, node):
            """constructor should not be invoked by user"""
            self._container = container
            self._node = node

        def element(self):
            """return the element stored at this position"""
            return self._node._element

        def __eq__(self, other):
            """return true if other is a position representing the same location"""
            return type(other) is type(self) and other._node is self._node

    def _validate(self, p):
        """return associated node, if position is valid"""
        if not isinstance(p, self.Position):
            raise TypeError('p must be proper position type')
        if p._container is not self:
            raise ValueError('p does not belong to this container')
        if p._node._parent is p._node:  # convention for deprecated nodes
            raise ValueError('p is no longer valid')
        return p._node

    def _make_position(self, node):
        """return position instance for given node """
        return self.Position(self, node) if node is not None else None

    # -------------------------- binary tree constructor --------------------------
    def __init__(self):
        """create an initially empty binary tree"""
        self._root = None
        self._size = 0

    # -------------------------- public accessors --------------------------
    def __len__(self):
        return self._size

    def root(self):
        return self._make_position(self._root)

    def parent(self, p):
        """return the position of p's parent"""
        node = self._validate(p)
        return self._make_position(node._parent)

    def left(self, p):
        node = self._validate(p)
        return self._make_position(node._left)

    def right(self, p):
        node = self._validate(p)
        return self._make_position(node._right)

    def num_children(self, p):
        node = self._validate(p)
        count = 0
        if node._left is not None:
            count += 1
        if node._right is not None:
            count += 1
        return count

    def _add_root(self, e):
        """place element e at the root of an empty tree and return new position"""
        if self._root is not None: raise ValueError('root exists')
        self._size = 1
        self._root = self._Node(e)
        return self._make_position(self._root)

    def _add_left(self, p, e):
        """
        create a new left child for position p,storing element e.
        return ValueError if Position p is invalid or p already has a left child
        """
        node = self._validate(p)
        if node._left is not None: raise ValueError('left child exists')
        node._left = self._Node(e, node)  # node is its parent
        return self._make_position(node._left)

    def _add_right(self, p, e):
        node = self._validate(p)
        if node._right is not None: raise ValueError('right child exists')
        node._right = self._Node(e, node)
        return self._make_position(node._right)

    def _replace(self, p, e):
        """Replace the element at position p with e, and return old element"""
        node = self._validate(p)
        old = node._element
        node._element = e
        return old

    def _delete(self, p):
        """
        delete the node at position p , and replace it with its child , if any.
        return the element that had been stored at position p.
        raise valueerror if position p is invalid or p has two children
        """
        node = self._validate(p)
        if self.num_children(p) == 2: raise ValueError('p has two children')
        child = node._left if node._left else node._right  # might be None
        if child is not None:
            child._parent = node._parent  # child s grandparent becomes parent
        if node is self._root:
            self.root = child  # child becomes root
        else:
            parent = node._parent
            if node is parent._left:
                parent._left = child
            else:
                parent._right = child
        self._size -= 1
        node._parent = node  # convention for deprecated node
        return node._element

    def _attach(self, p, t1, t2):
        """attach tree t1 and t2 as left and right subtrees of external p"""
        node = self._validate(p)
        if not self.is_leaf(p): raise ValueError('position must be leaf')
        if not type(self) is type(t1) is type(t2):  # all 3 trees must be same type
            raise TypeError('tree types must match')
        self._size += len(t1) + len(t2)
        if not t1.is_empty():
            t1._root._parent = node  # attached t1 as left subtree of node
            node._left = t1._root
            t1._root = None  # set t1 instance to empty
            t1._size = 0
        if not t2.is_empty():  # attached t2 as right subtree of node
            t2._root.parent = node
            node._right = t2
            t2._root = None
            t2._size = 0

    def __iter__(self):
        """generate an iteration of the tree's elements"""
        for p in self.positions():
            yield p.element()

    def preorder(self):
        """generate a preorder iteration of positions in the tree"""
        if not self.is_empty():
            for p in self._subtree_preorder(self.root()):
                yield p

    def _subtree_preorder(self, p):
        """generate a preorder iteration of positions in subtree rooted at p"""
        yield p
        for c in self.children(p):
            for other in self._subtree_preorder(c):
                yield other

    def positions(self):
        """generate an iteration of the tree's positions"""
        return self.preorder()  # return entire preorder iteration

    def postorder(self):
        """generate a postorder iteration of positions in the tree"""
        if not self.is_empty():
            for p in self._subtree_postorder(self.root()):
                yield p

    def _subtree_postorder(self, p):
        """generate a postorder iteration of positions in subtree rooted at p"""
        for c in self.children(p):
            for other in self._subtree_postorder(c):
                yield other
        yield p

    def breadthfirst(self):
        """generate a breath-first iteration of the positions of the tree"""
        if not self.is_empty():
            fringe = LinkedQueue()  # known positions not yet yielded
            fringe.enqueue(self.root())  # starting with the root
            while not fringe.is_empty():
                p = fringe.dequeue()  # remove from front of the queue
                yield p  # report this position
                for c in self.children(p):
                    fringe.enqueue(c)  # add children to back of queue

    def inorder(self):
        """generate a breath-first iteration of the positions"""
        if not self.is_empty():
            for p in self._subtree_inorder(self.root()):
                yield p

    def _subtree_inorder(self, p):
        """generate an inorder iteration of positions in subtree rooted at p"""
        if self.left(p) is not None:  # if left child exists, traverse its subtree
            for other in self._subtree_inorder(self.left(p)):
                yield other
        yield p  # visit p between its subtrees
        if self.right(p) is not None:  # if right child exists, traverse its subtree
            for other in self._subtree_inorder(self.right(p)):
                yield other


if __name__ == '__main__':
    T = LinkedBinaryTree()
    T.root()
    T.is_empty()
    T._add_root(10)
    root = T.root()
    T._add_left(root, 8)
    T._add_right(root, 30)
    left = T.left(root)
    right = T.right(root)

    print('sibling of left: ', T.sibling(left).element())

    print('***preorder***')
    for p in T.preorder():
        print(p.element())

    print('***postorder***')
    for p in T.postorder():
        print(p.element())

    print('***inorder***')
    for p in T.inorder():
        print(p.element())

    print('***breadthfirst***')
    for p in T.breadthfirst():
        print(p.element())