队列

数据结构 队列

1、队列的定义及应用

队列（queue）是一种先进先出的线性表，只允许在一端进行插入操作，在另一端进行删除操作。允许数据插入的这一端称为队尾，允许数据删除的这一端称为队头。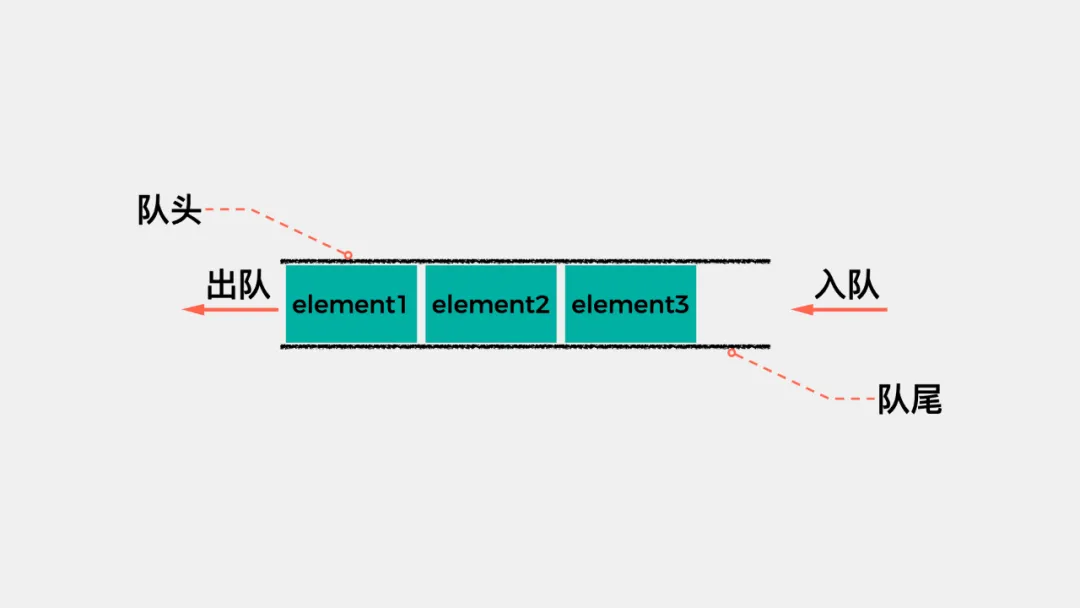队列在生活中的一个应用是客户服务的排队等待。比如去移动营业厅办理业务时，对于刚去的几个人，由于客户服务专员都是空闲的，所以可以一对一处理相关业务。在处理过程中，如果有其他客户过来，那么就需要排队等待，当某个客户服务专员处理完一个业务后，队首的客户就可以到相应窗口处理其业务了。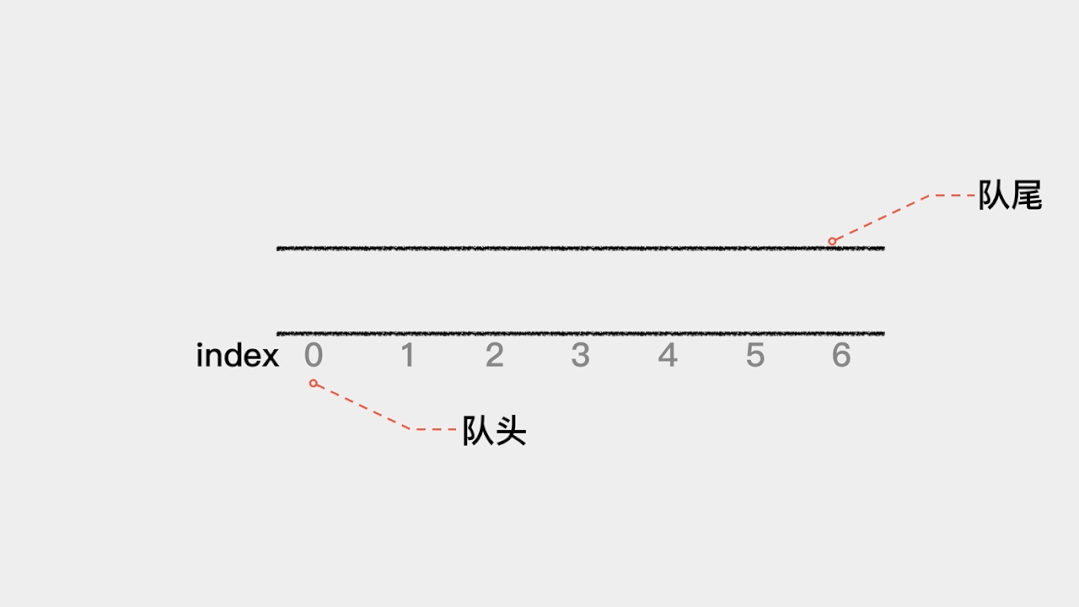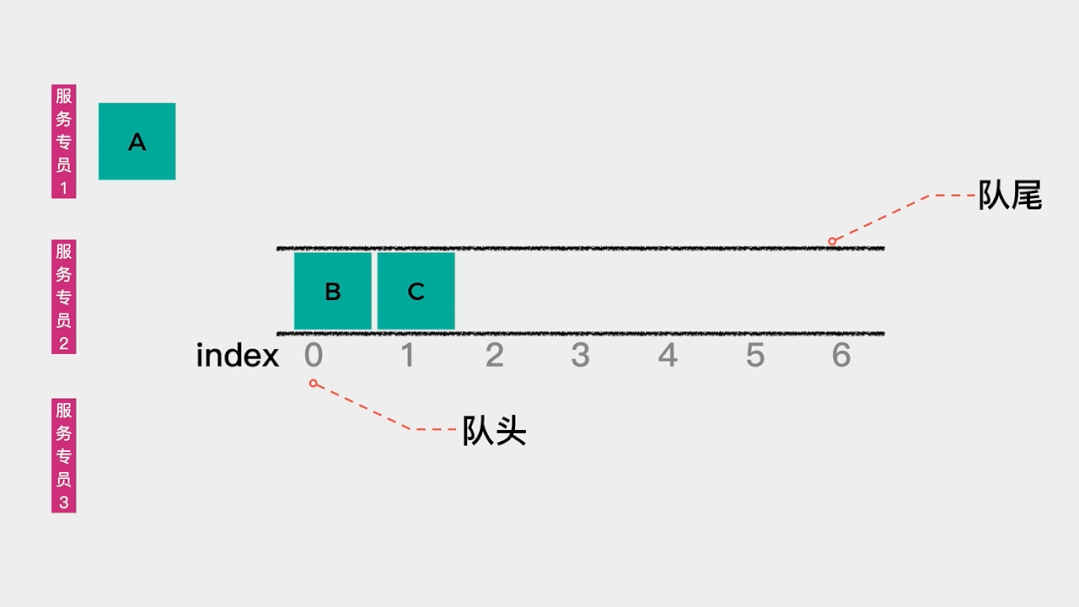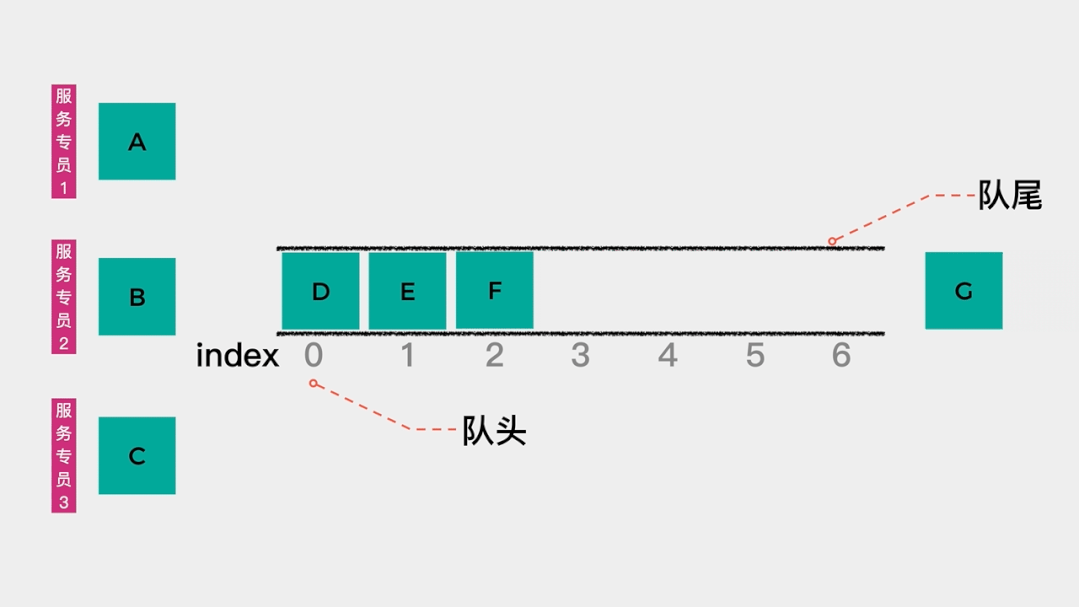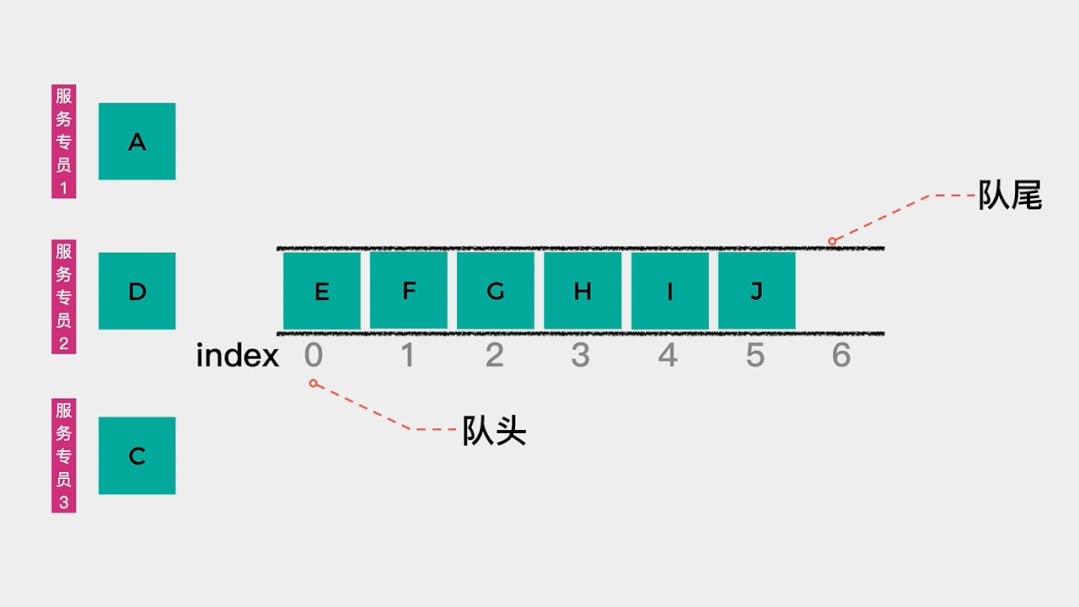

2、顺序队列的介绍及实现

顺序队列是指由数组实现的队列。队列有队头和队尾，对于用数组实现的队列，在这里规定索引为0的一端作为队头。那么，入队操作就是就是向数组中添加元素，这时不需要移动任何元素。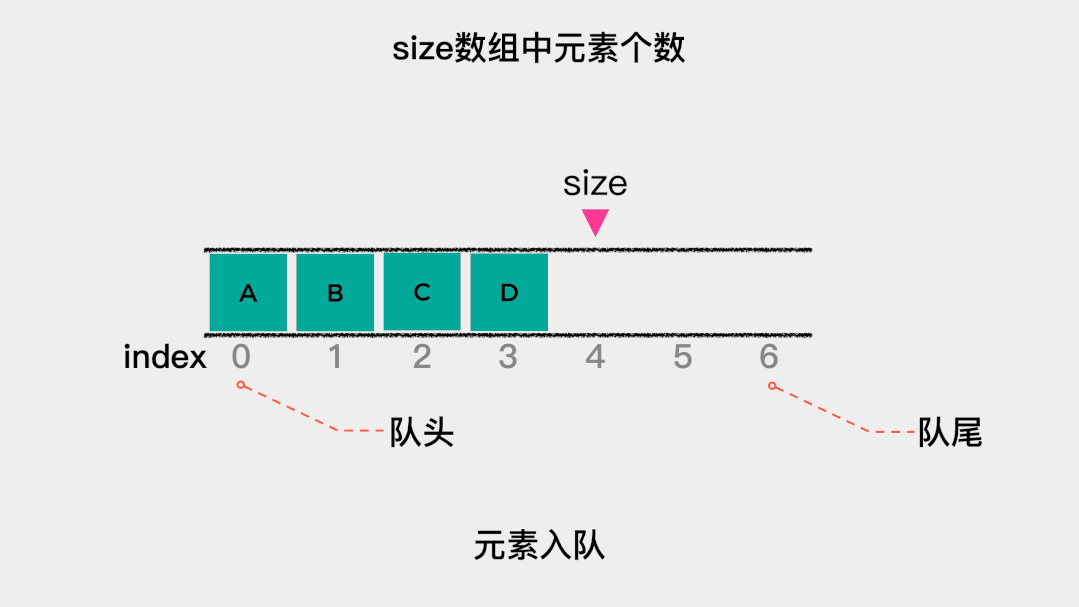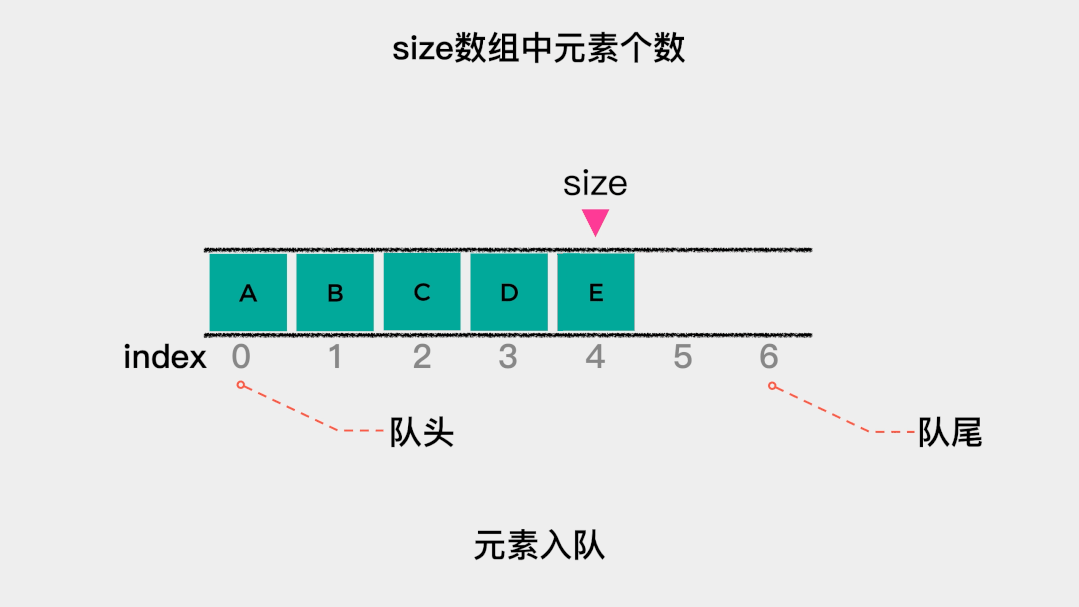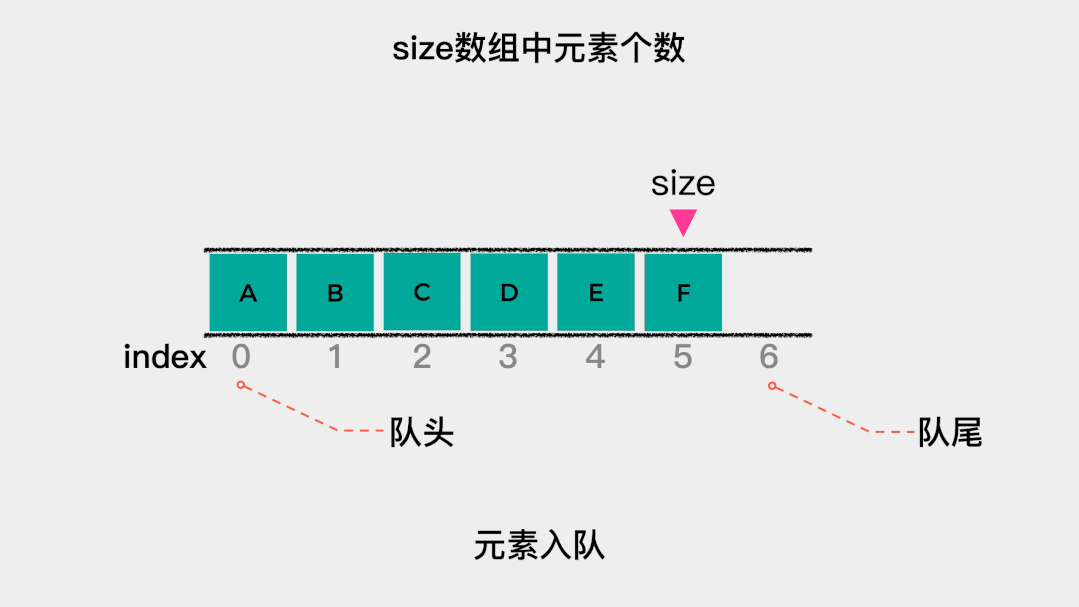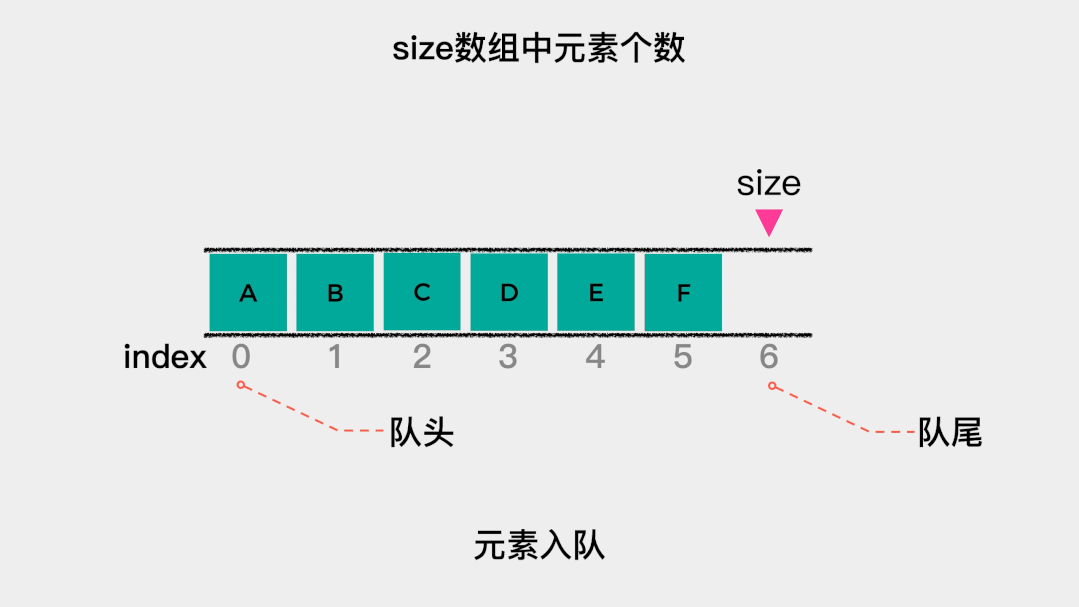当队列满时，需要做的是扩容，在这里扩容为原来的2倍。也就是当数组满时，新建一个容量为原数组2倍的数组，然后将原数组中的元素依次拷贝到新数组中。这里入队操作只有在数组容量不足时，才会做一次数据移动，根据根据摊还分析法，其时间复杂度为O(1)。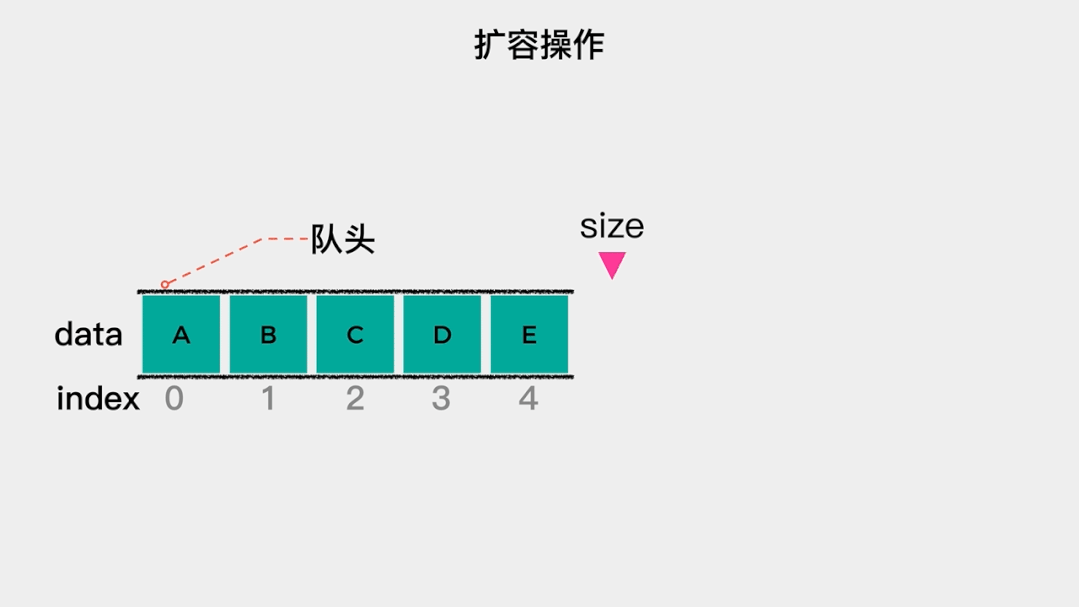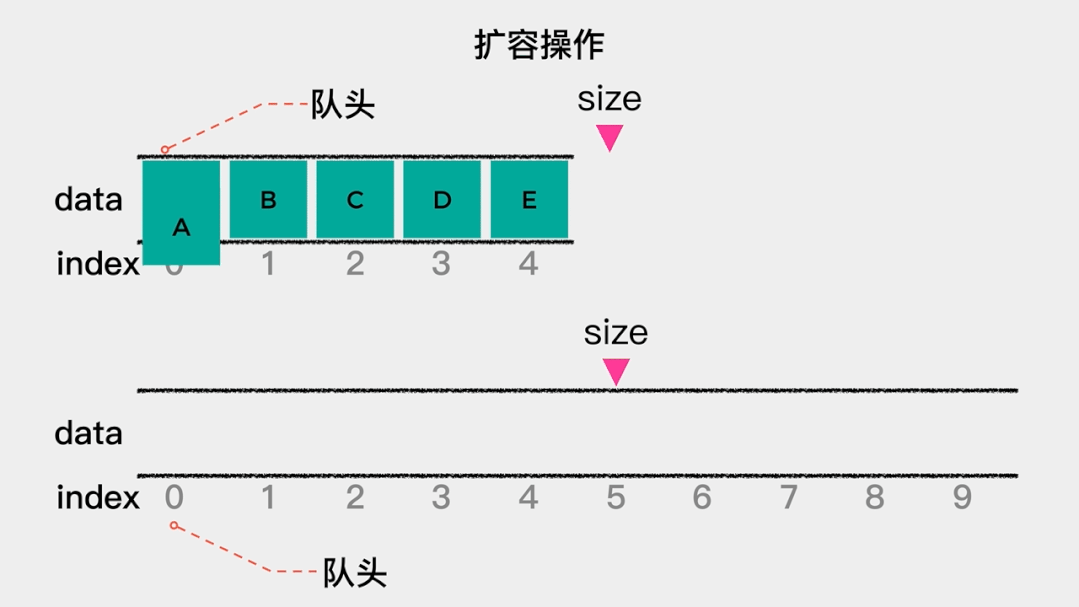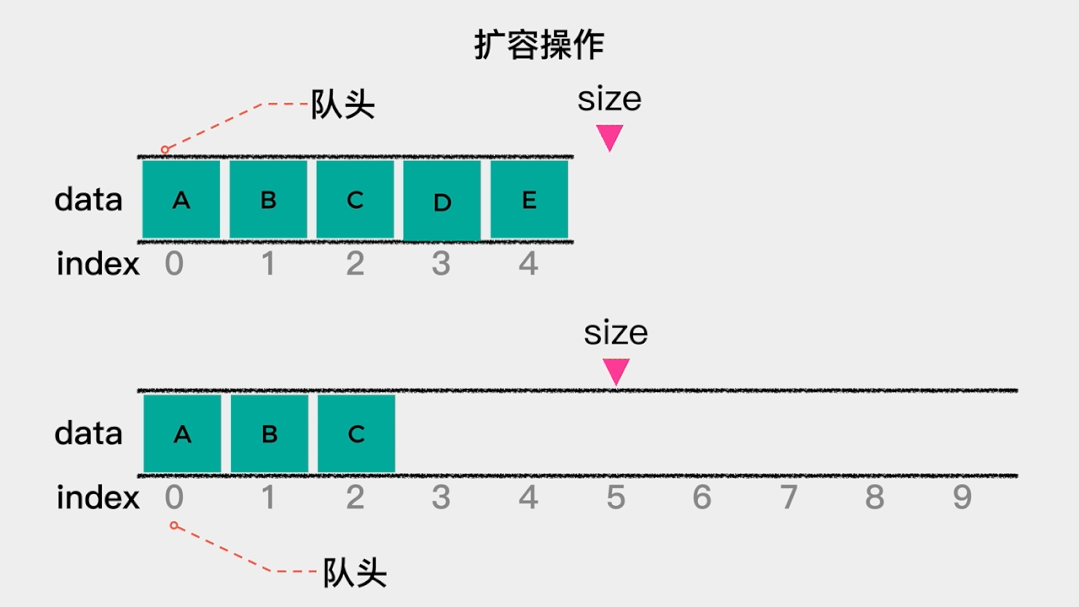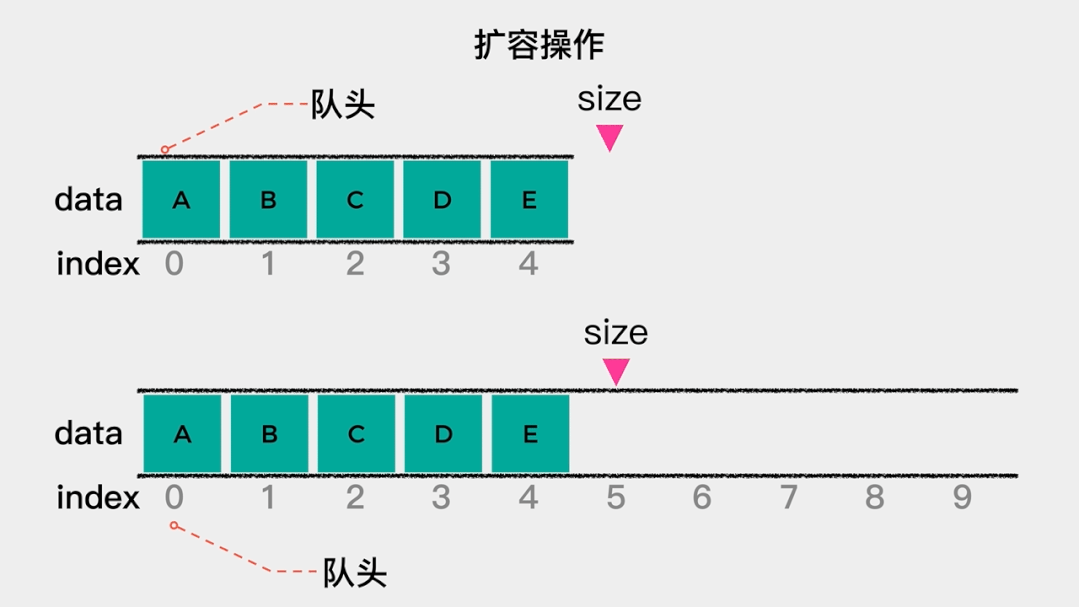接着看下出队操作的时间复杂是多少？出队操作，是将索引为0的元素移除。由于规定索引为0的这一端是队头，因此，每次队头元素出队后，都需要将队列中剩余的元素向前移动一位。所以出队操作的时间复杂度是O(n)。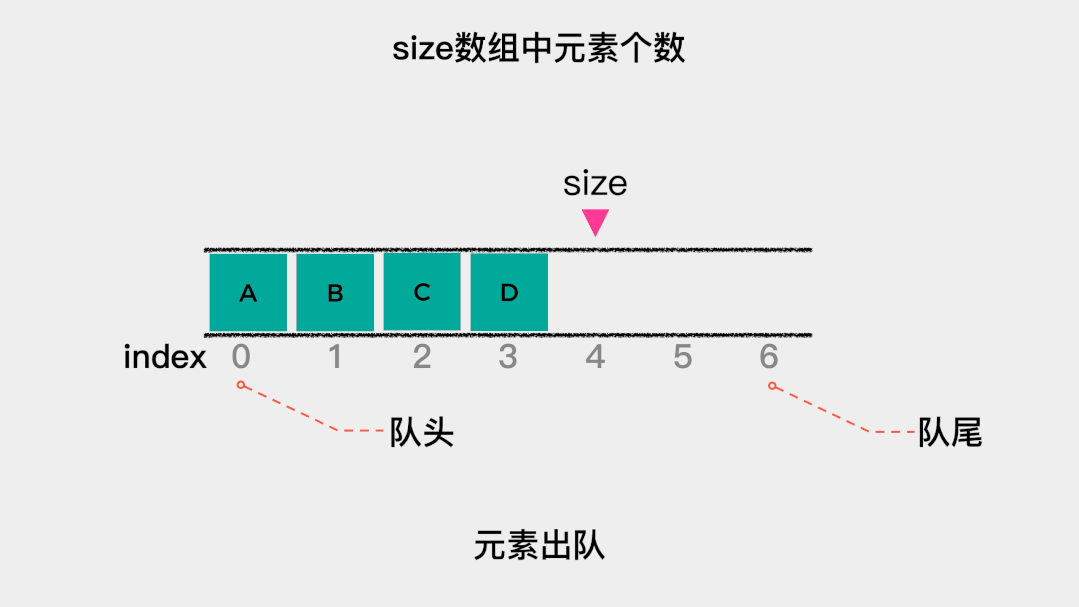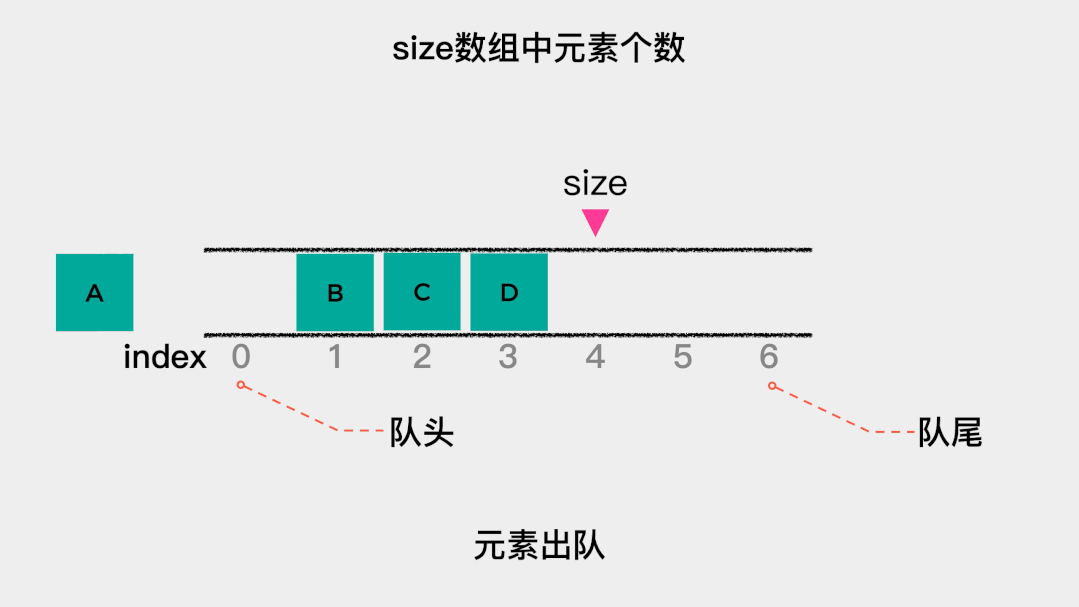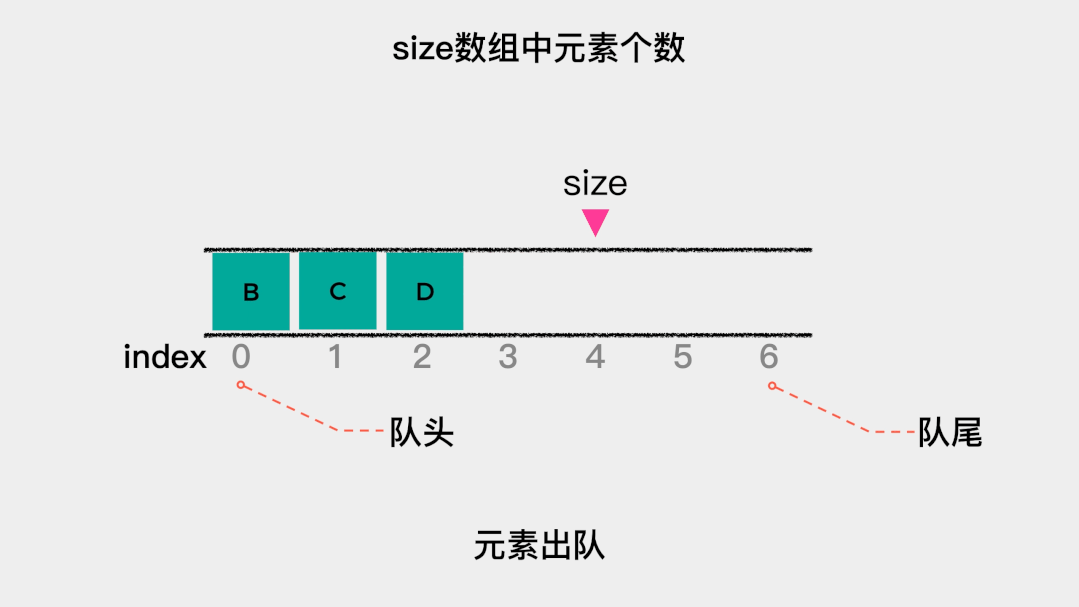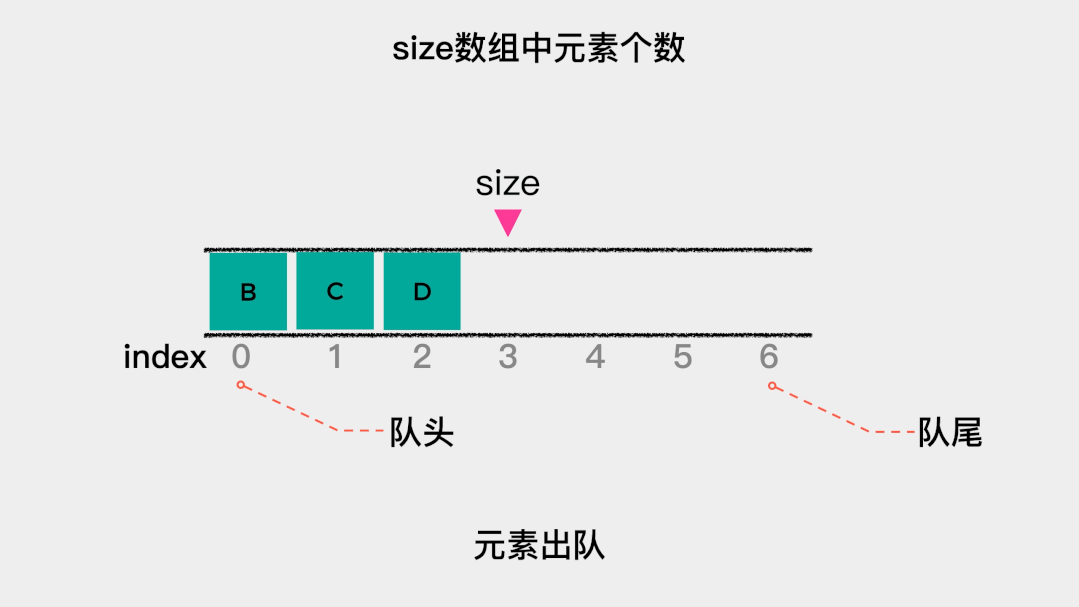顺序队列的代码实现如下：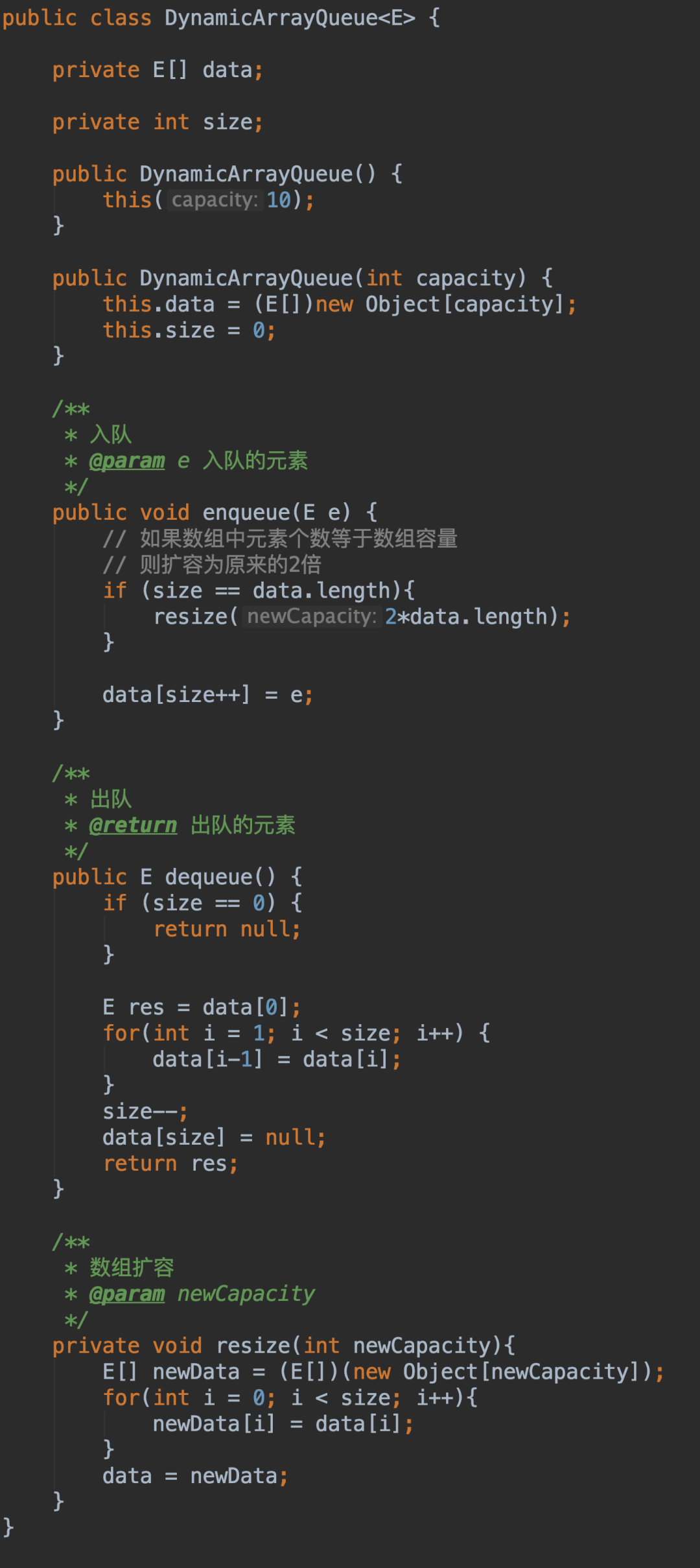

3、循环队列的介绍及实现

上述顺序队列的实现中，把索引为0的位置当做队头，这使得每当元素出队时，都要将其后面的所有元素向前移动一个位置。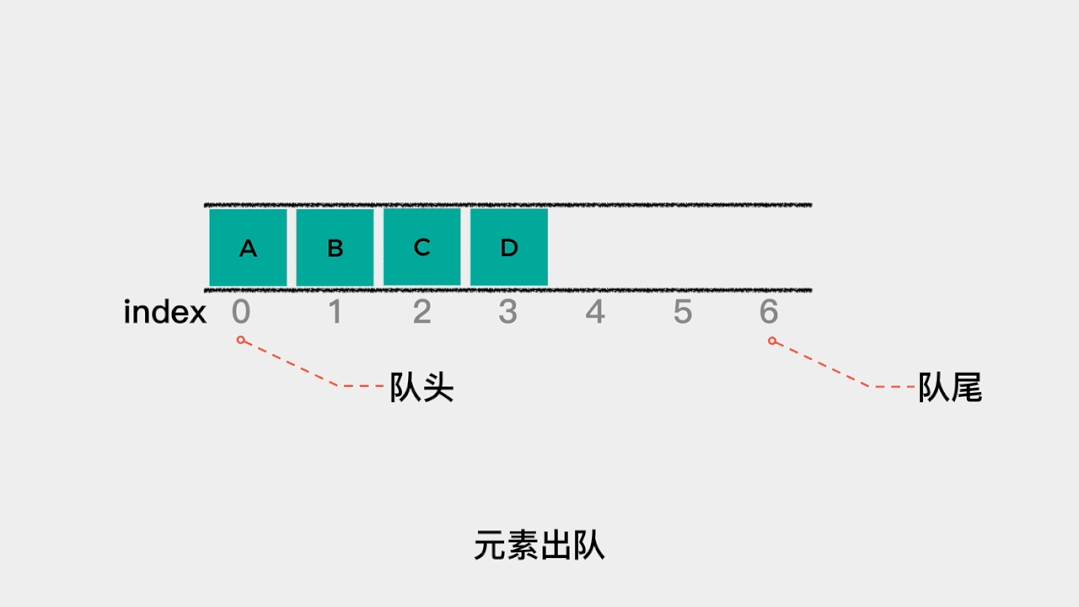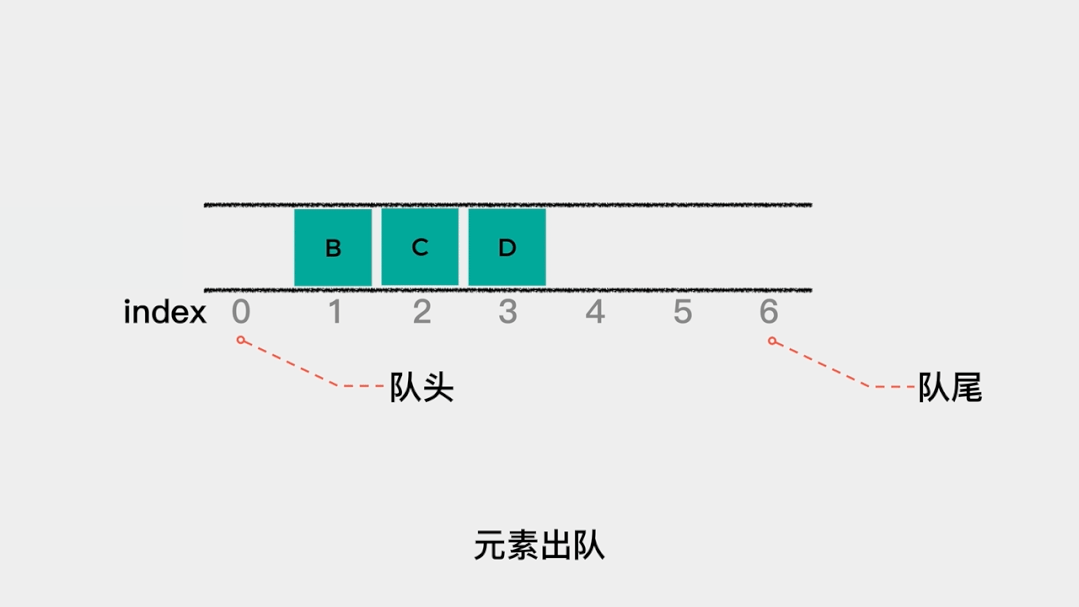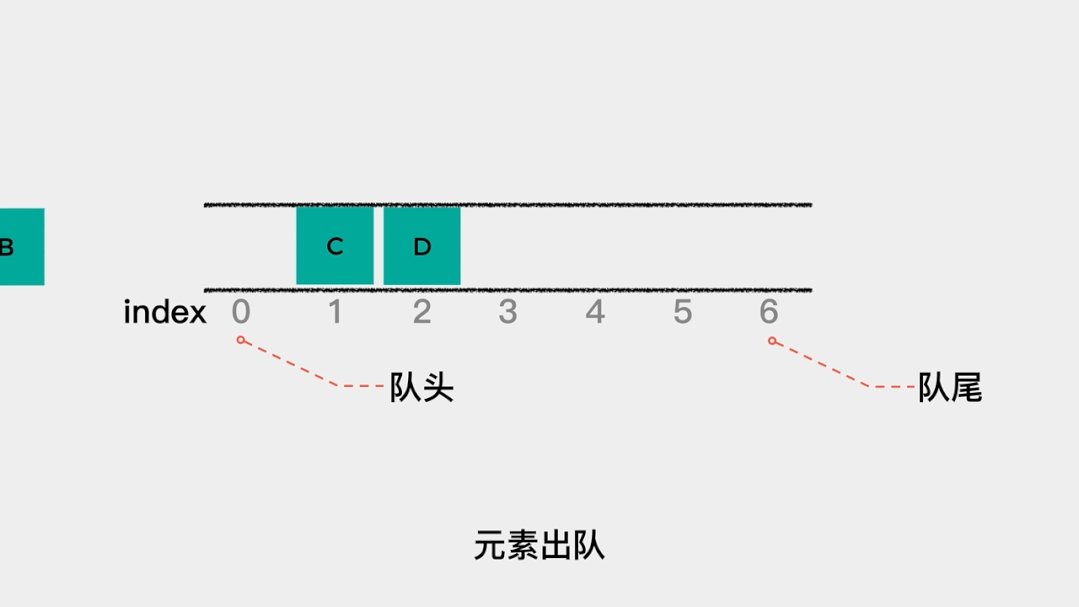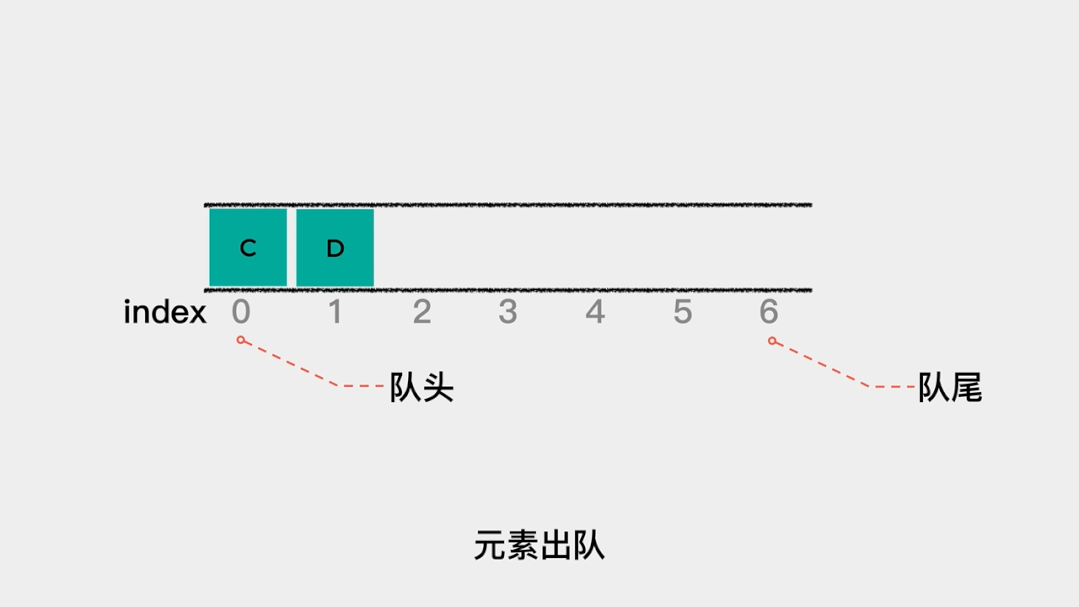当数据量很大时，这个操作就非常耗时了。那么，可不可以减少数据移动的次数呢？可以的。就是分别用head和tail指向队列的队头和队尾。这样，当有元素入队时，tail++就可以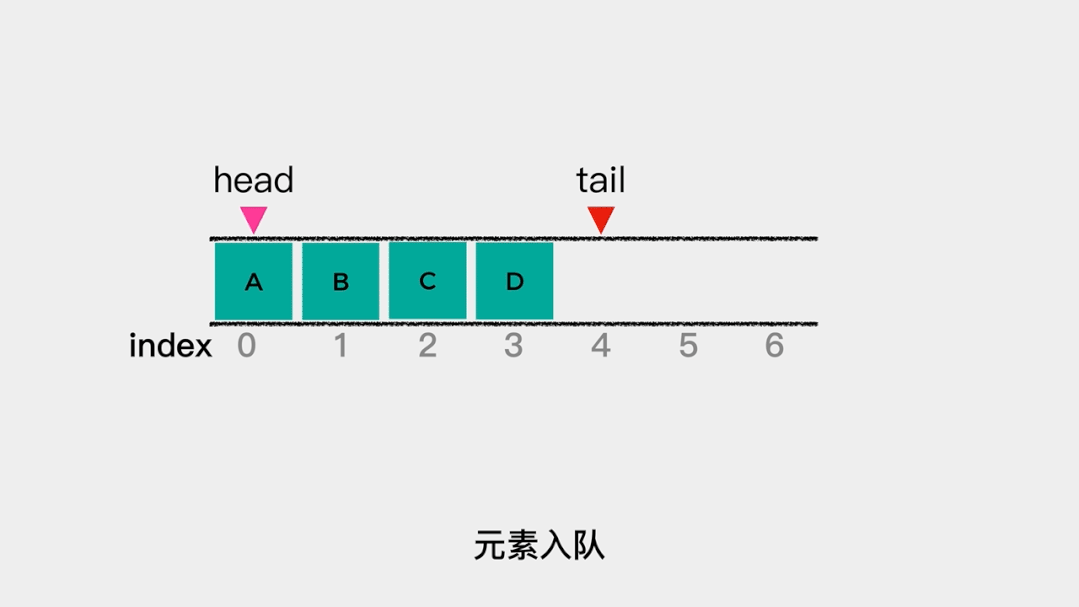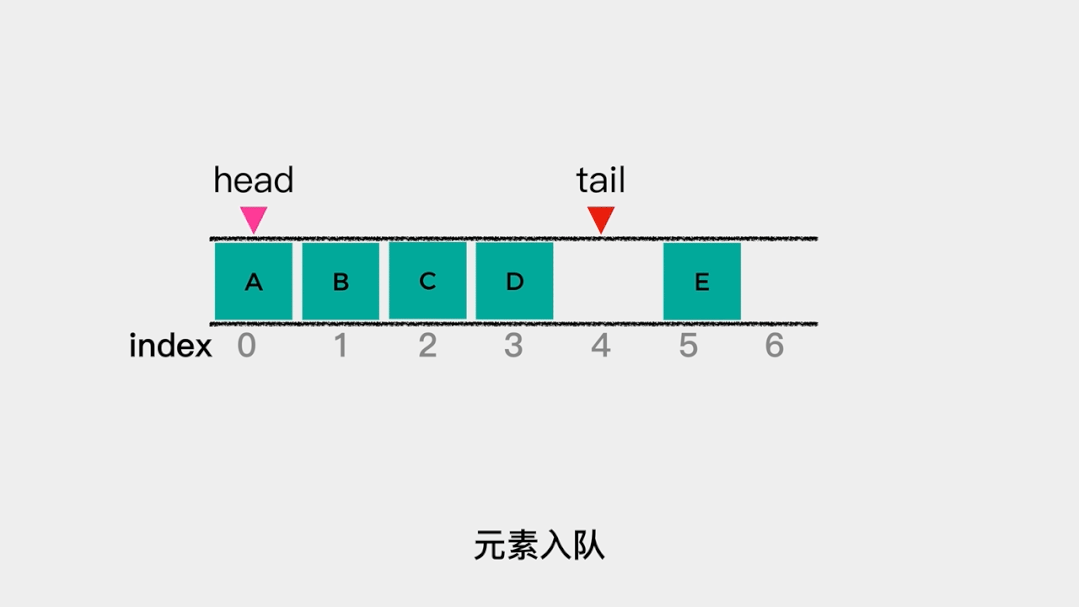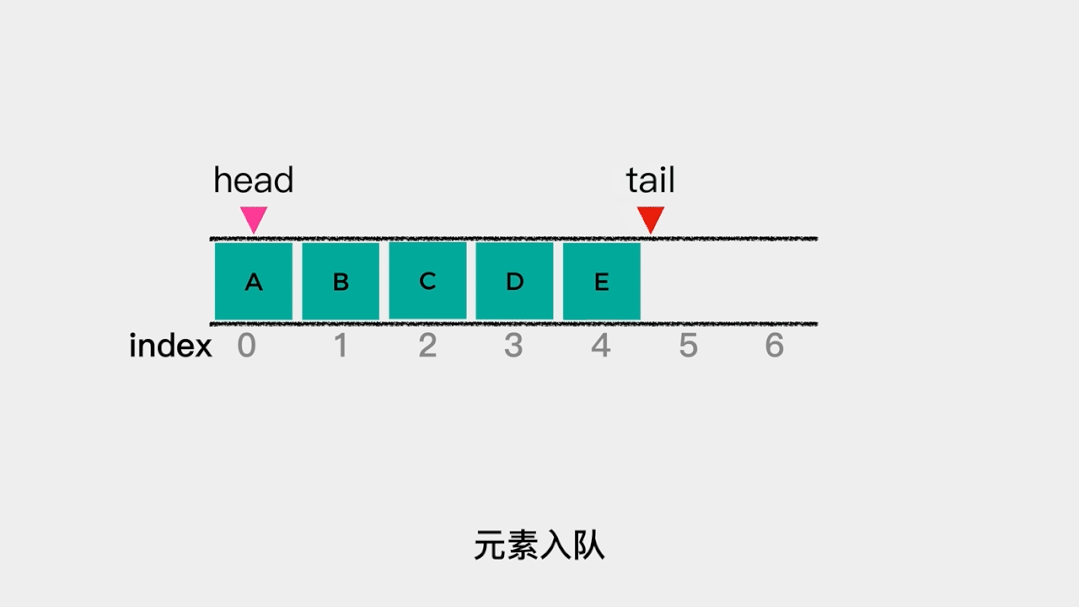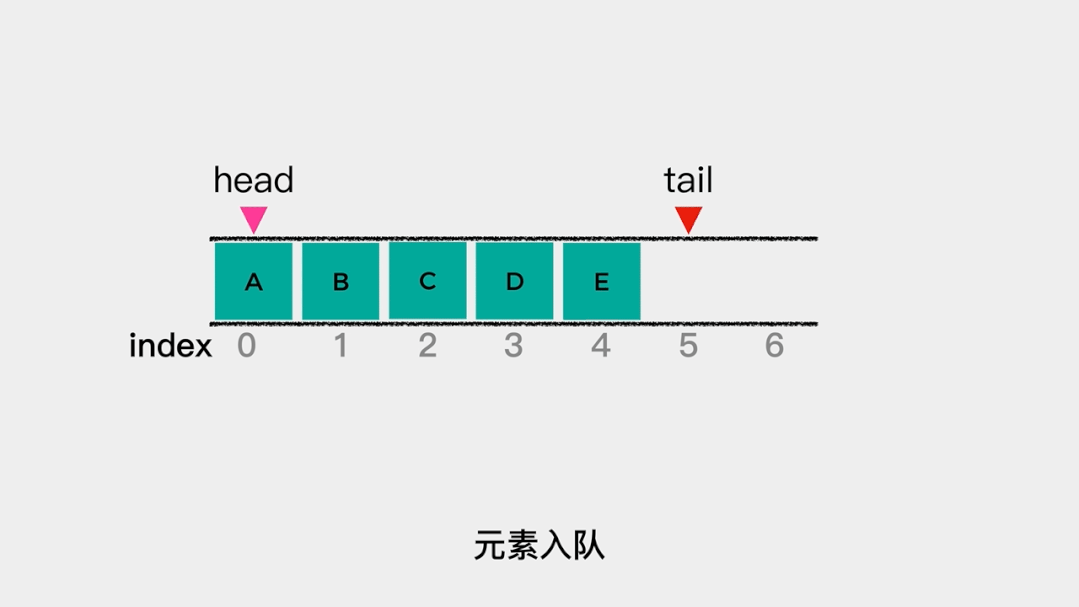；同样的，当有元素出队时，head++就可以了。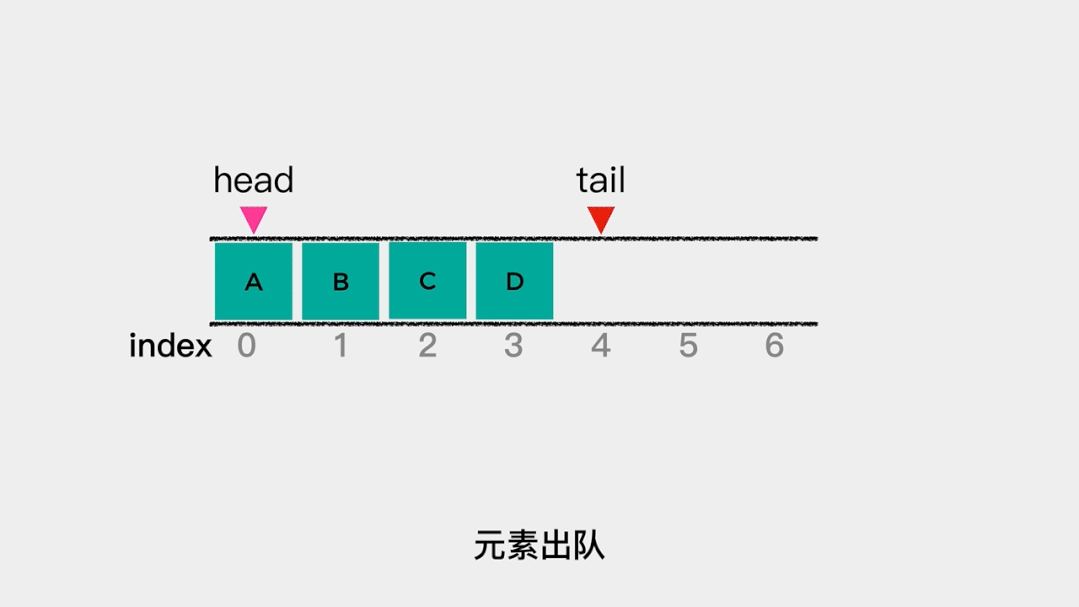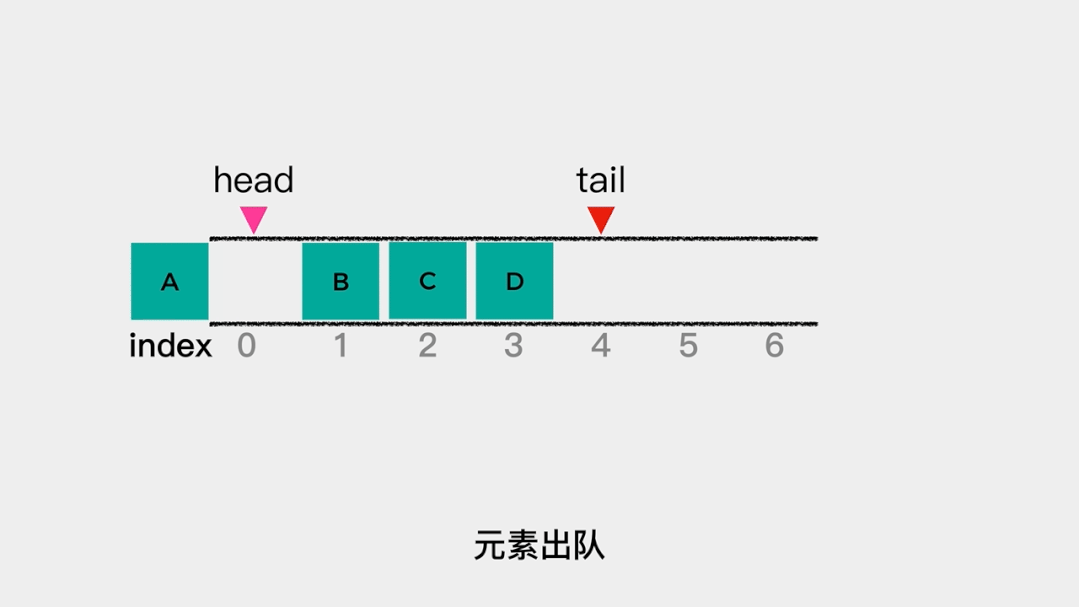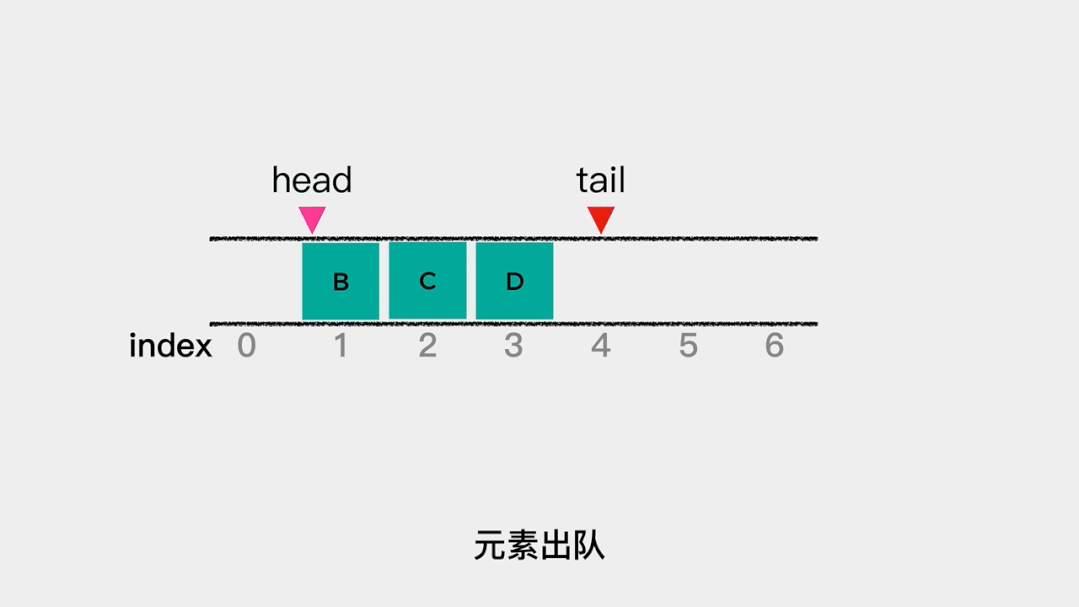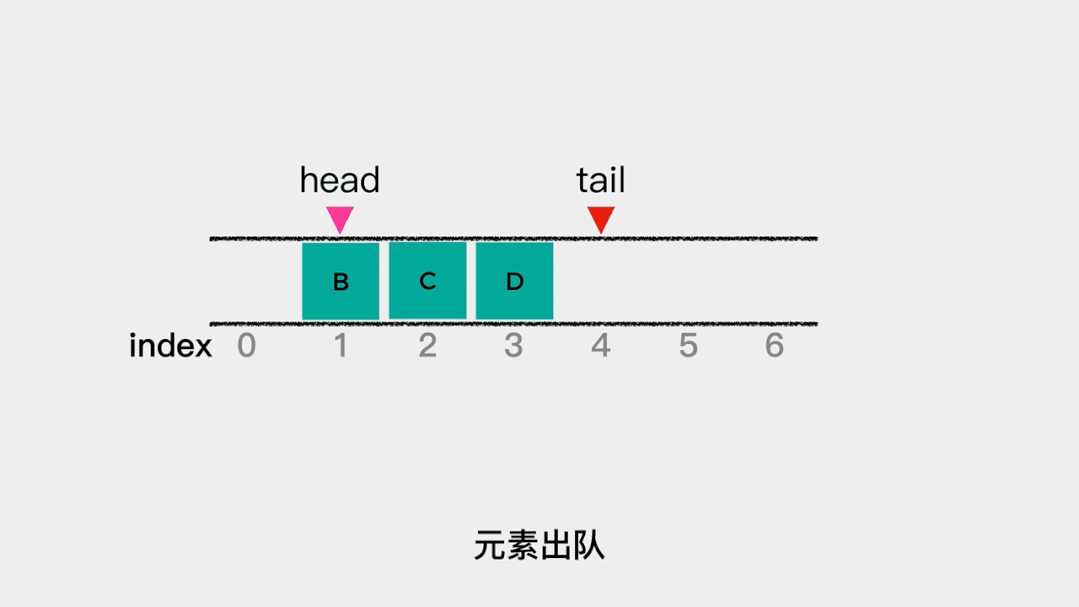在这里分别用head和tail指向队列的队头和队尾，那么当队列为空时，head和tail指向同一个位置，也就是说**head==tail**表示队列为空。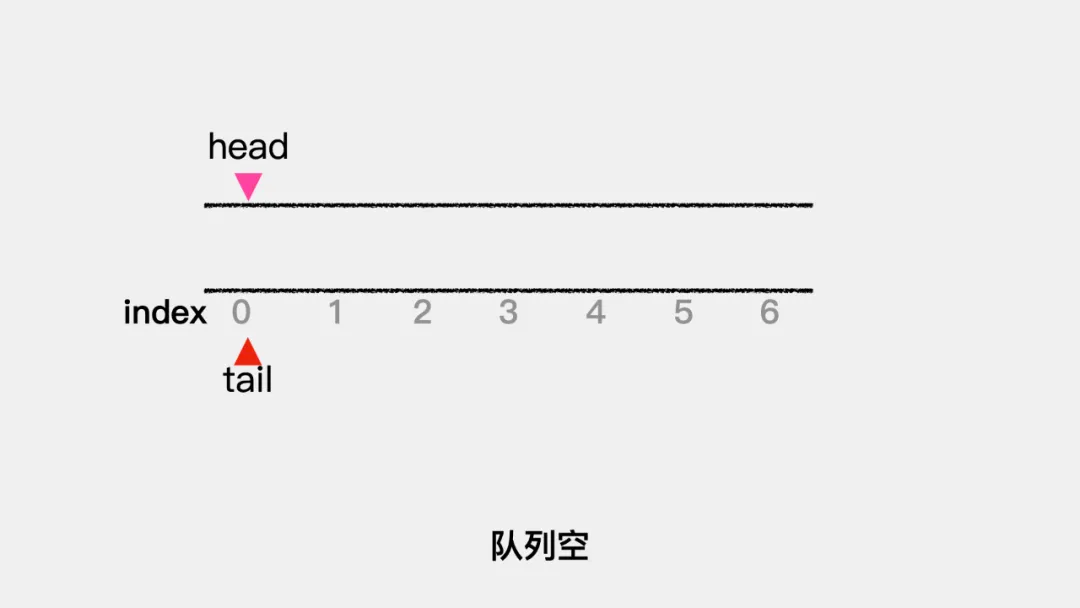
那么什么时候会触发数据移动呢？就是当tail的值等于数组容量，head不等于0时。因为，如果tail的值等于数组容量且head=0，则表示队列满了。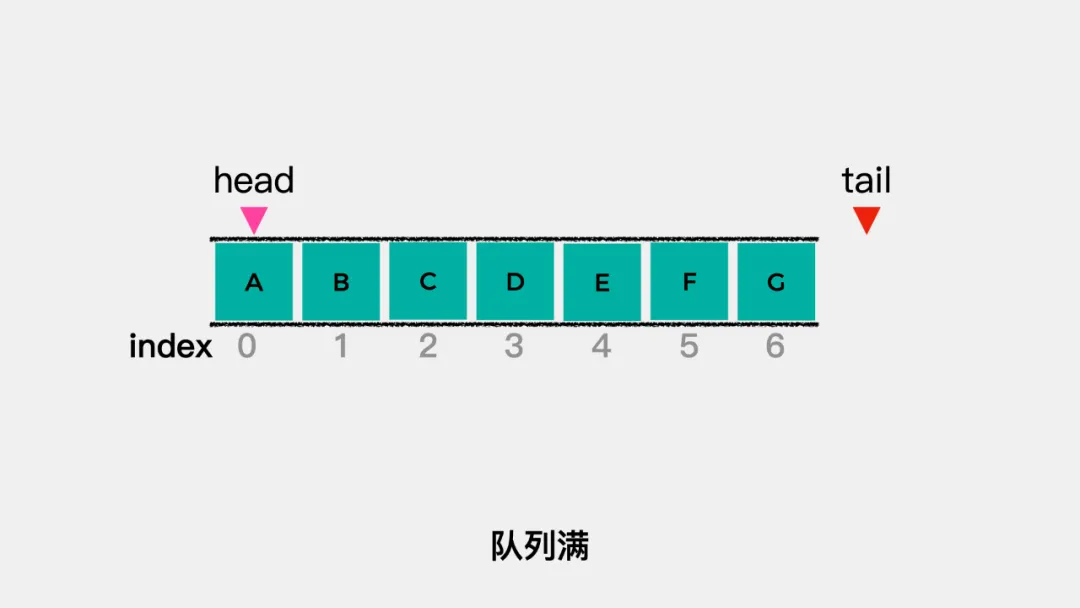队列不满时，数据迁移具体动画演示如下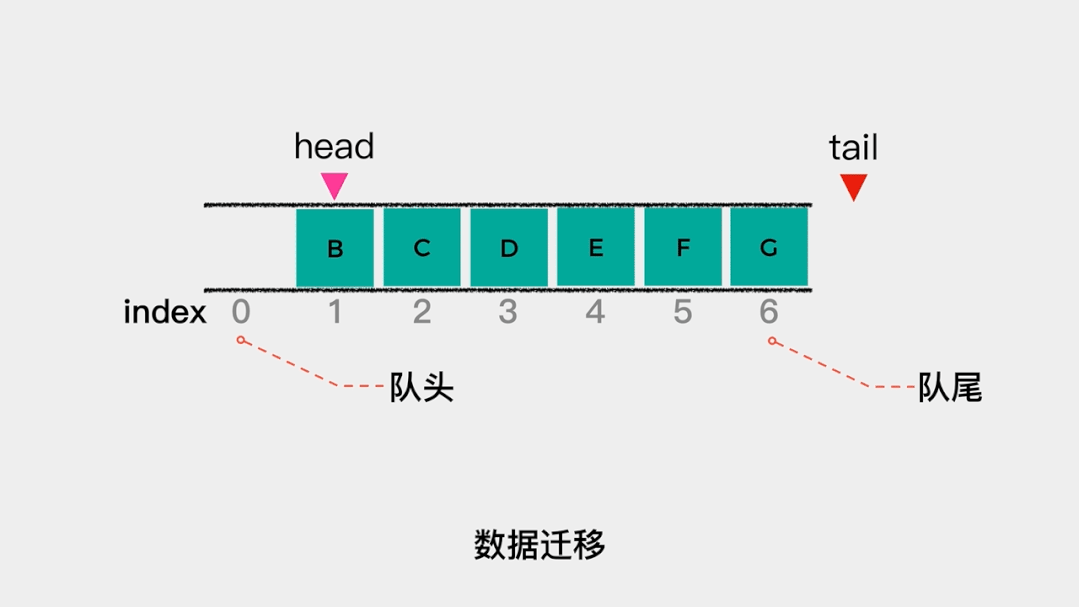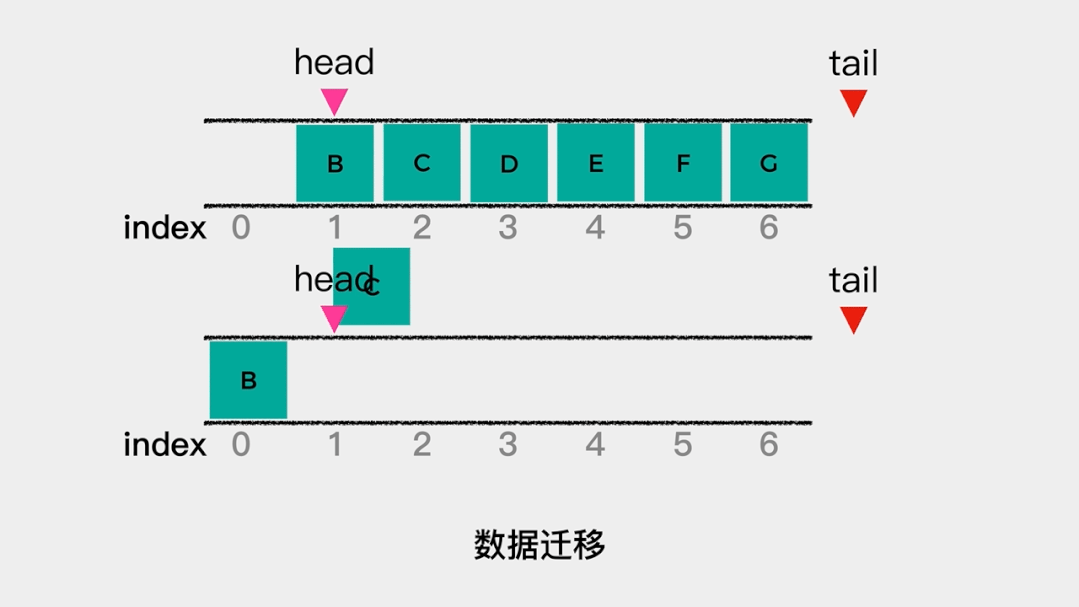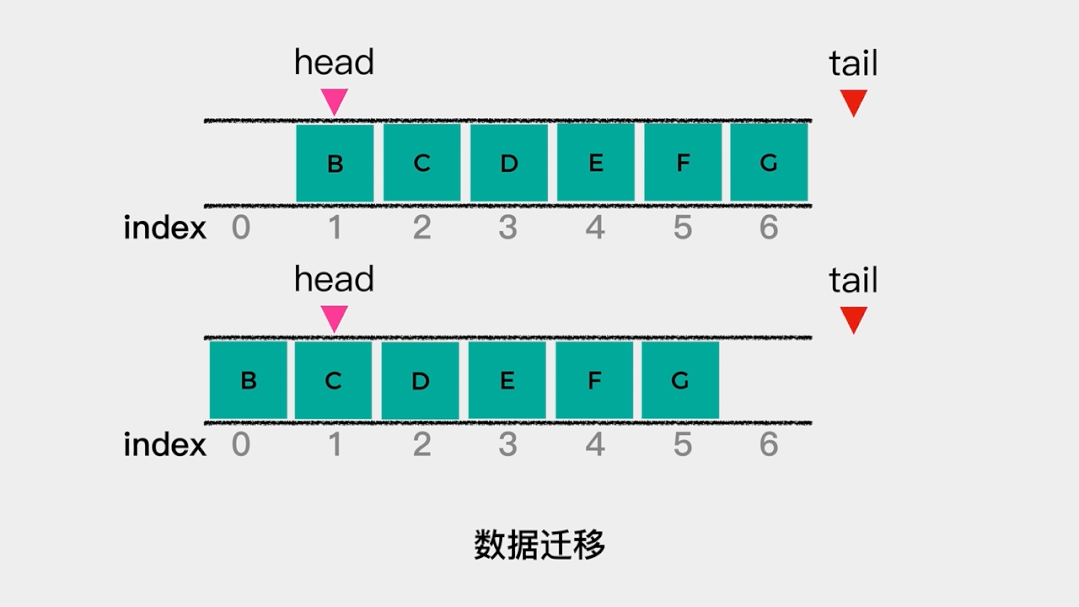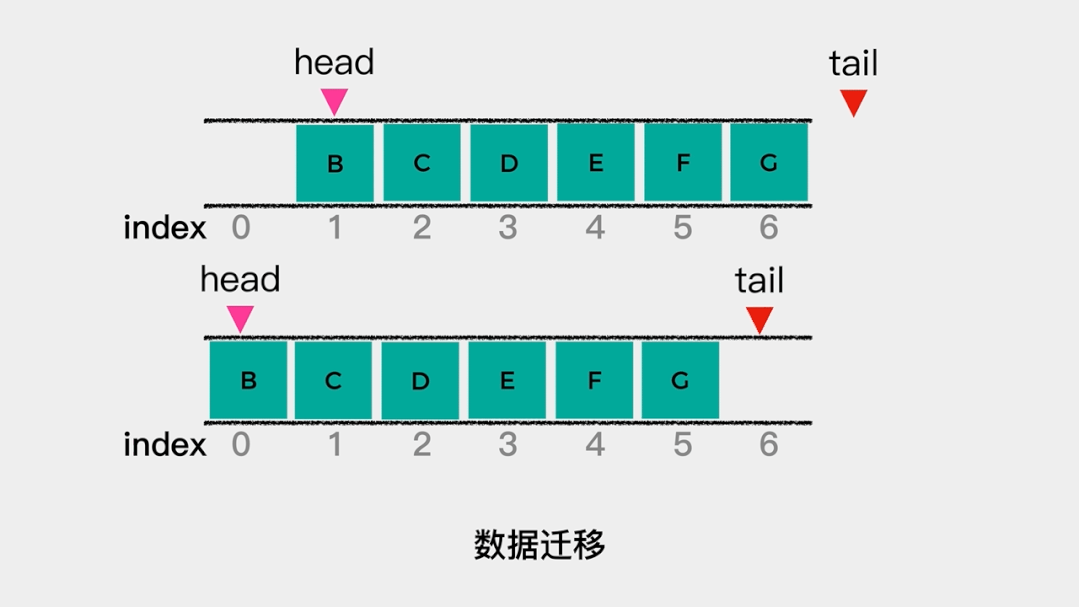：这样出队操作的时间复杂度就降低了。这时用数组实现队列的代码如下：

那么，能不能更进一步，就是当tail的值等于数组容量且head不等于0时（如下图所示），在这种情况下，直接将元素添加到空的位置呢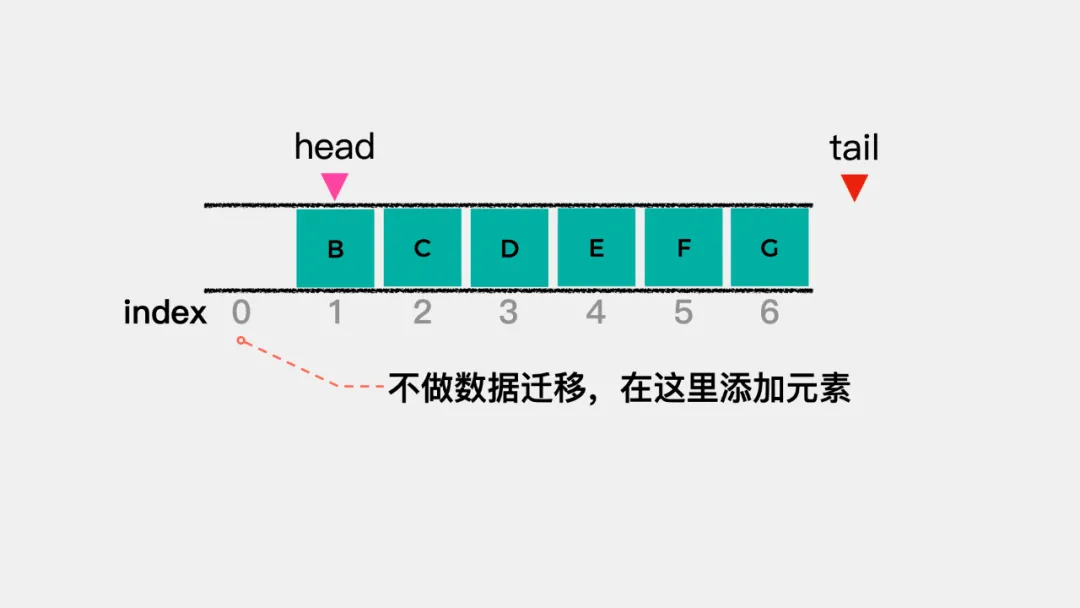？也就是说tail的值等于数组容量时，将其指向索引为0的位置，即在从头开始添加元素。把这种头尾相接的顺序存储结构称为循环队列。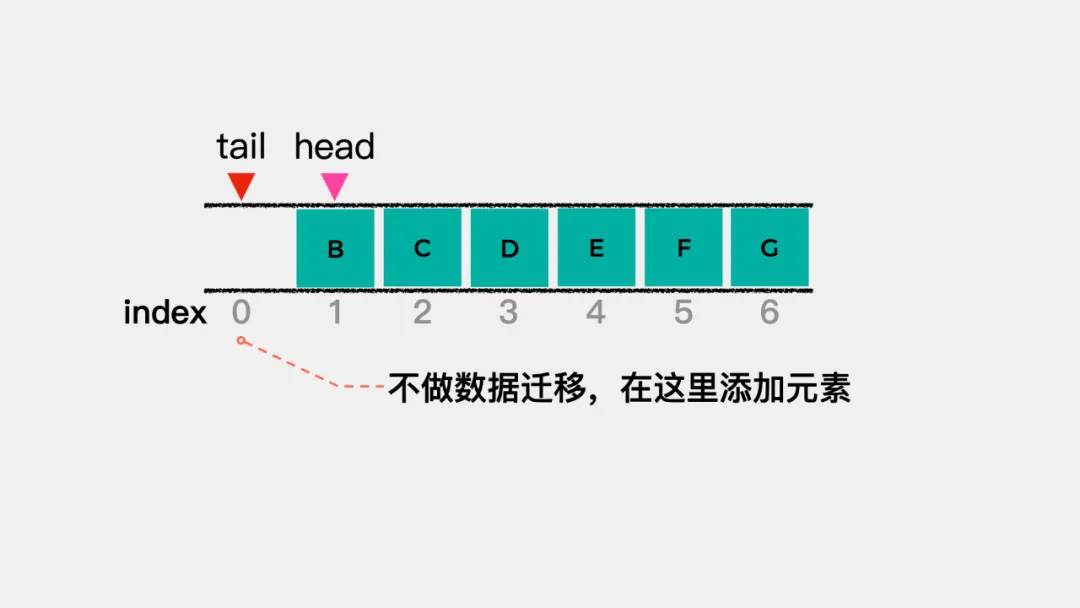在索引为0的位置添加元素后，tail需要加1，即向后移动一个位置。此时，head==tail，也就是说队列满了。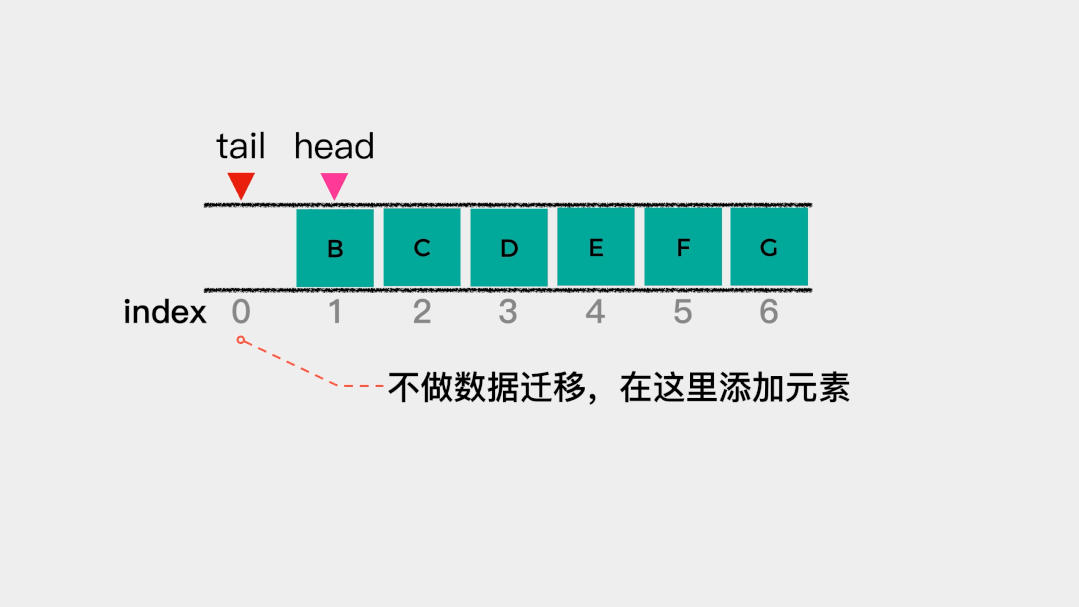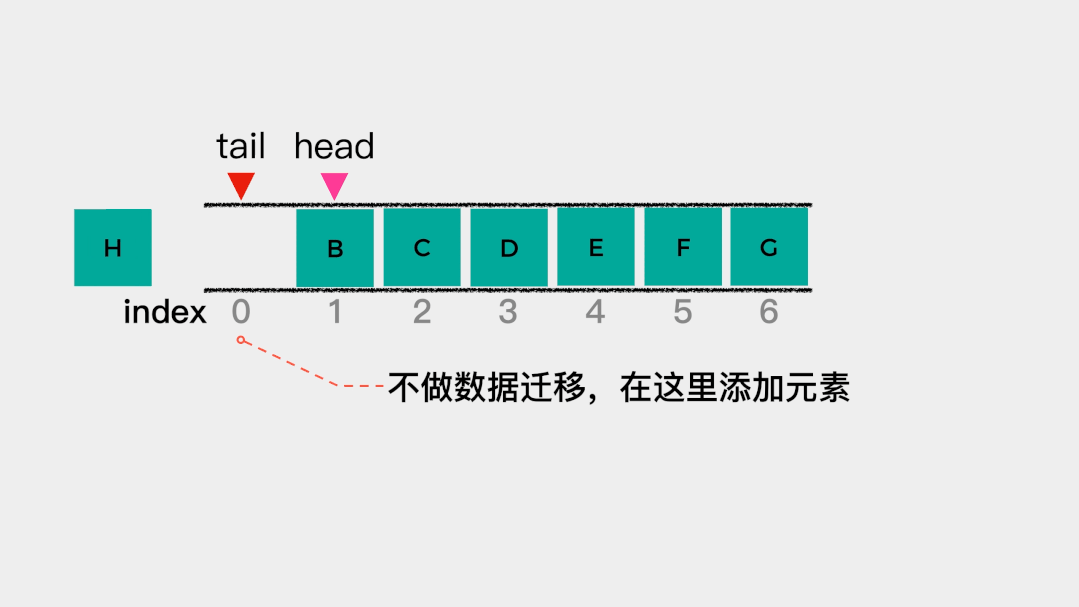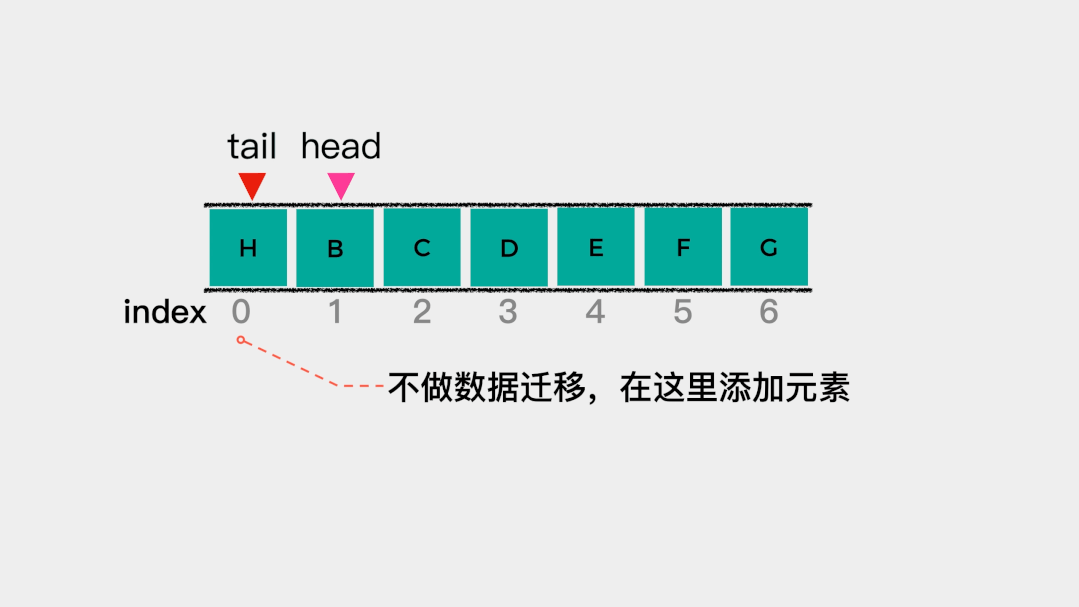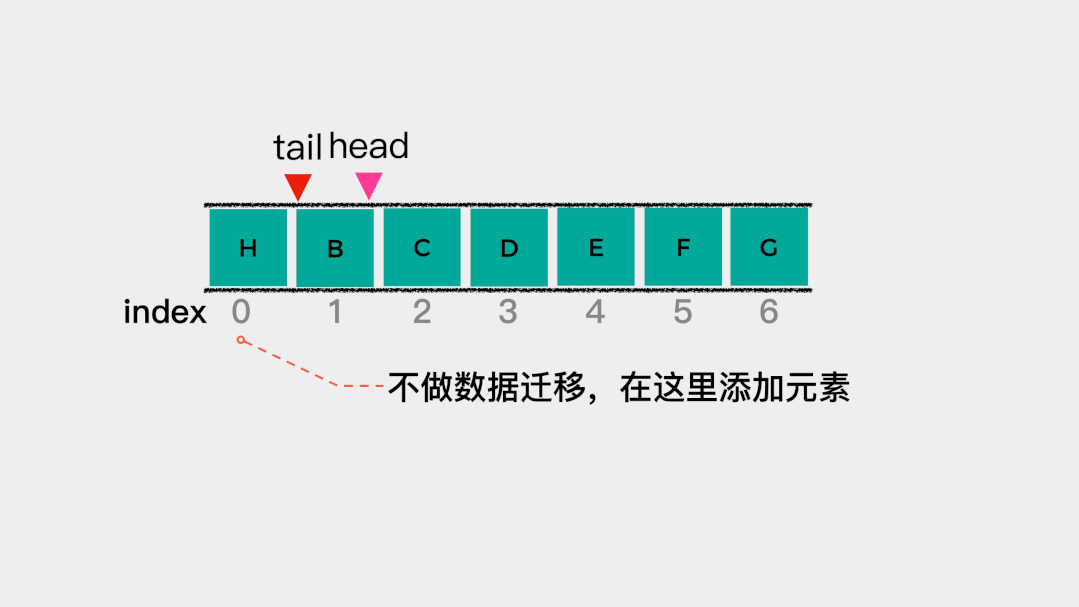但是，在上面已经规定head==tail是表示队列为空。这时该怎么办呢？可以规定**(tail+1)%data.length==head**表示队列满了。接着，对(tail+1)%data.length==head表示队列满做一个解释：

• 如下图，tail=6时，(6+1)%7=0=head，此时队列满。

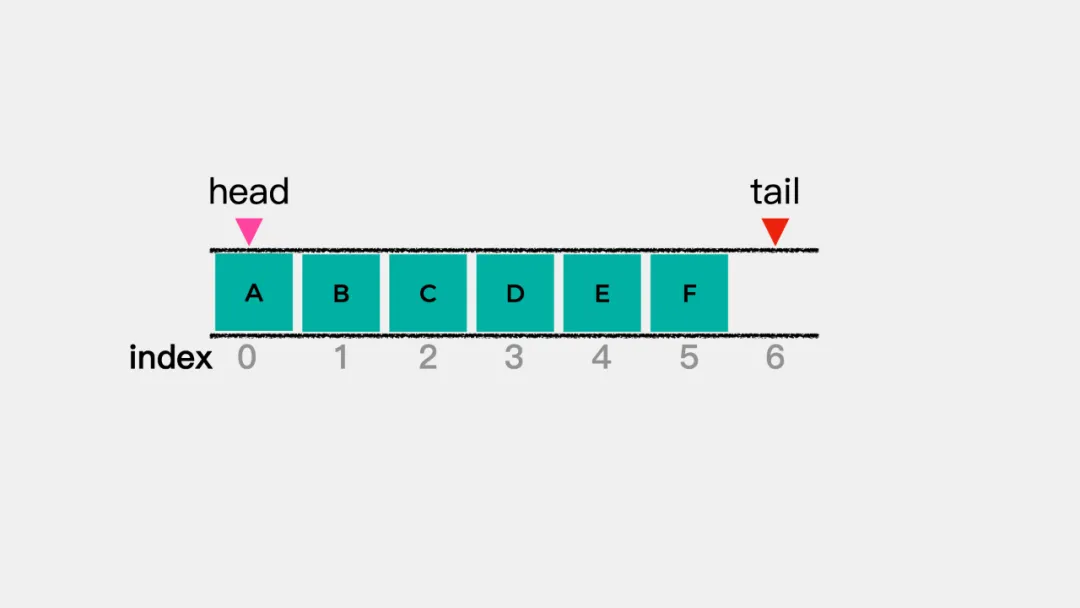
• 下图中，tail再次指向0，此时(0+1)%7=1=head，队列满。

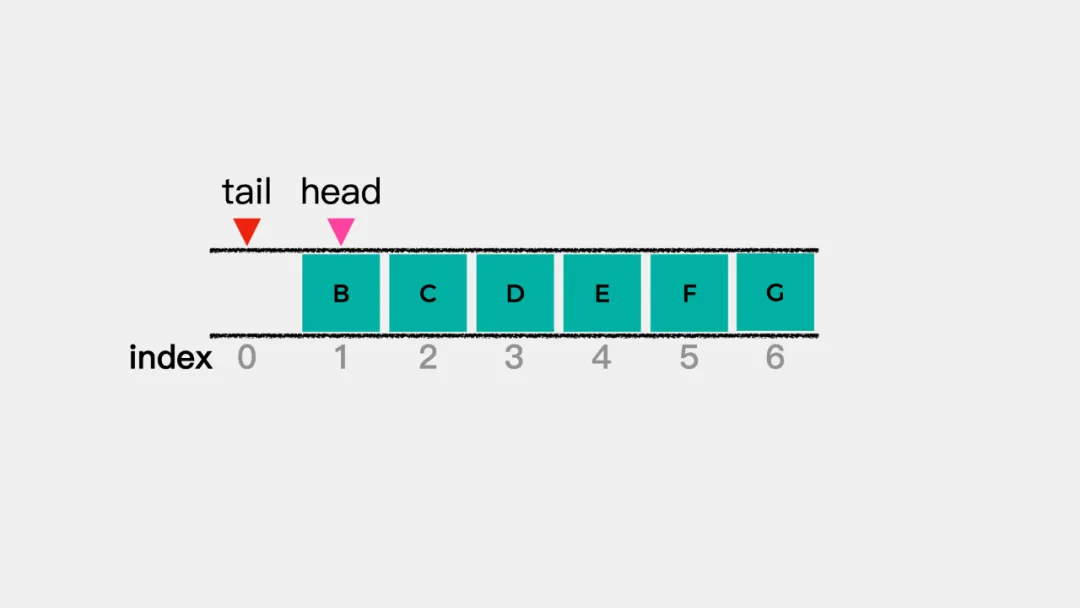
• 下图中，tail=1，此时(1+1)%7=2=head，队列满。

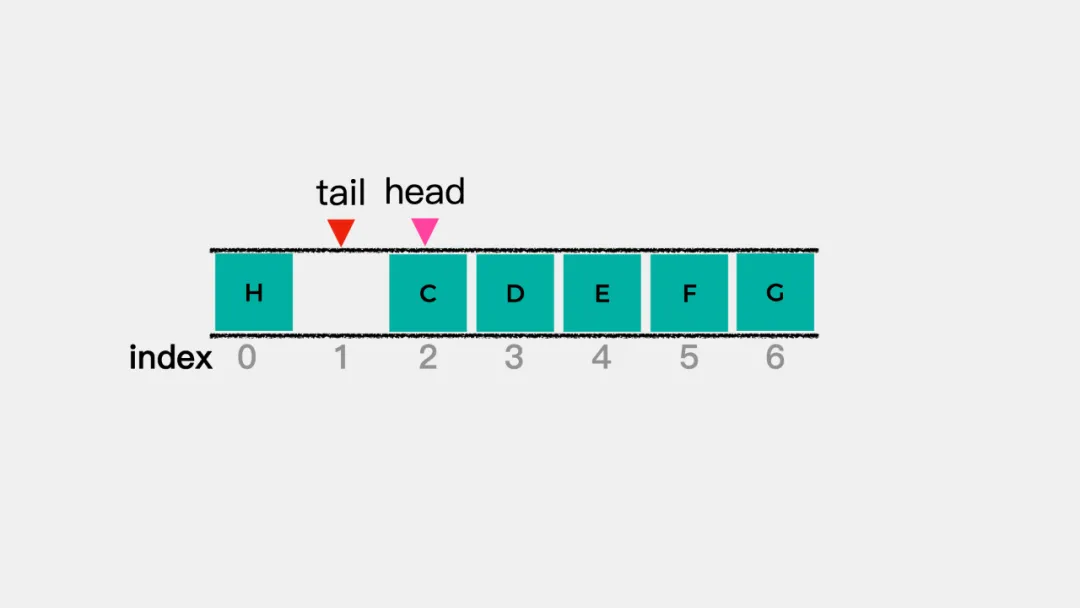根据上述分析，在循环队列中，head==tail表示队列为空；(tail+1)%data.length==head表示队列满，此时，数组中浪费一个存储空间。基于数组实现的循环队列代码示例如下：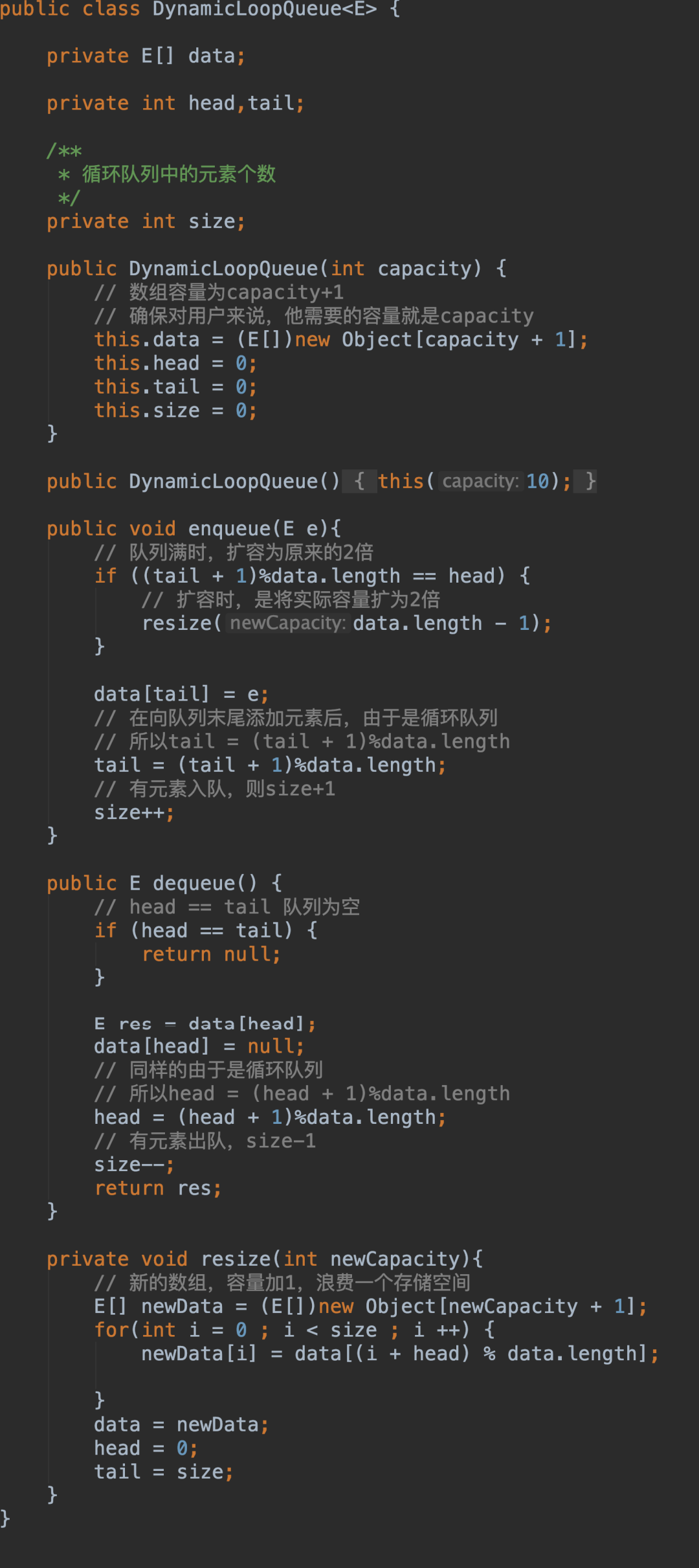

4、链式队列的介绍及实现

链式队列是指用链表实现的队列。常见的链表结构如下图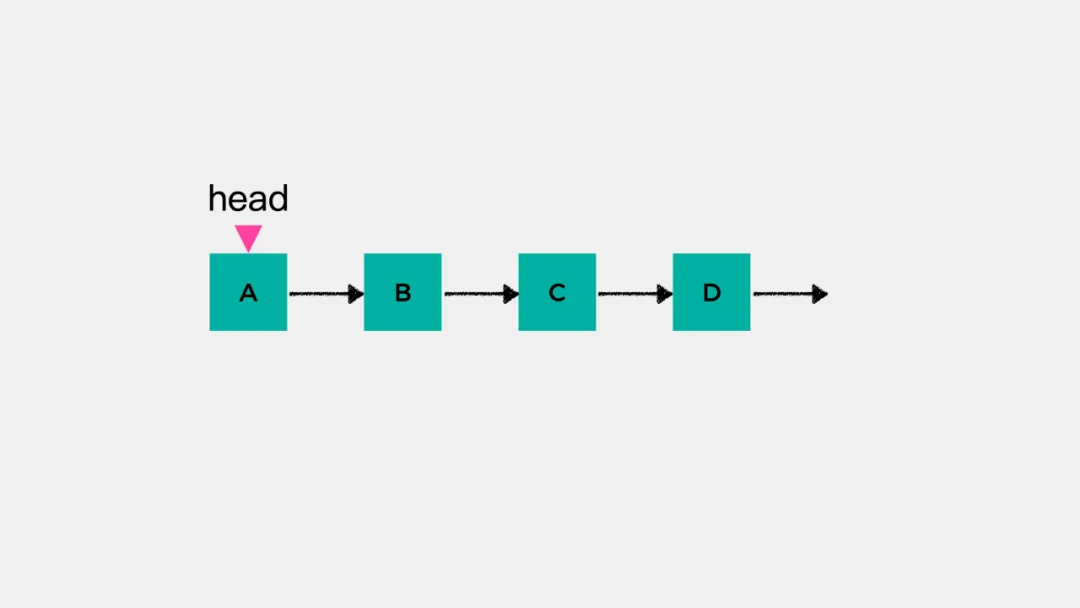：对于这样的链表不论是在head这一端添加元素还是删除元素，都是容易的。在链表头节点head之前添加元素的时间复杂度是O(1)，动画演示如下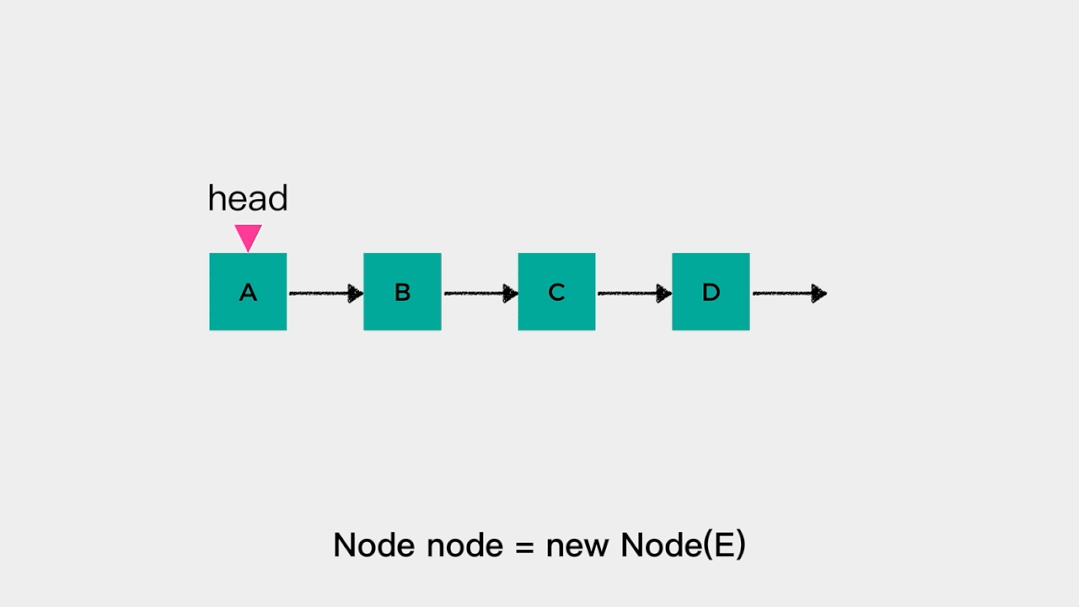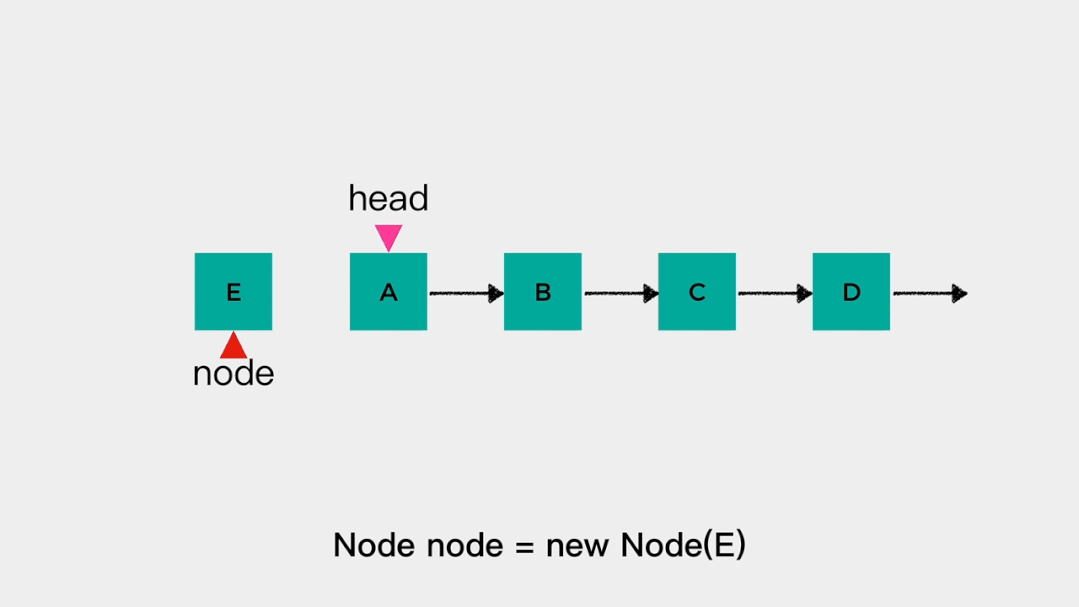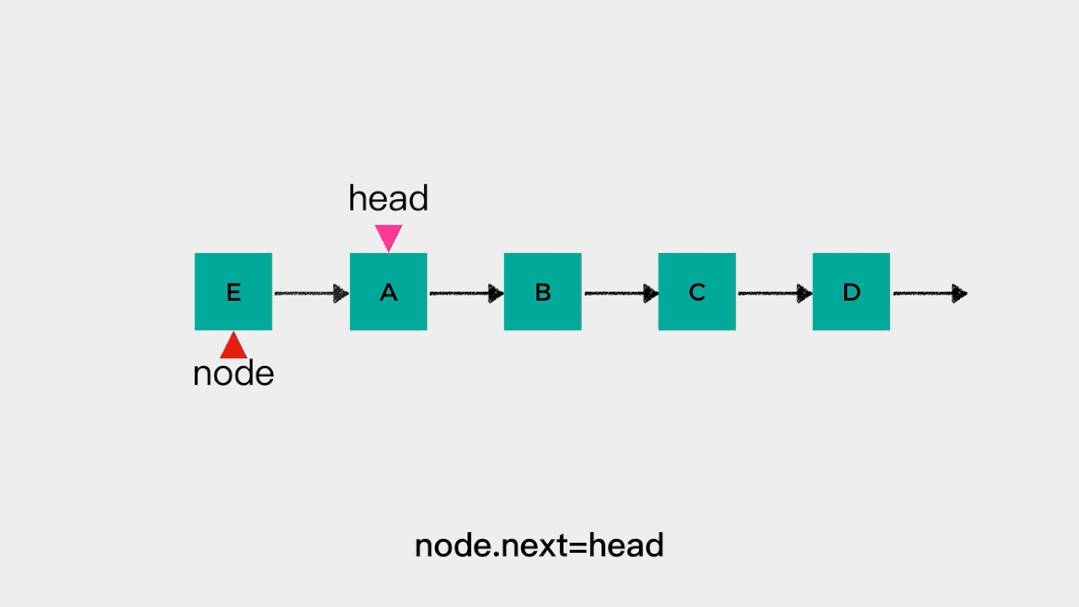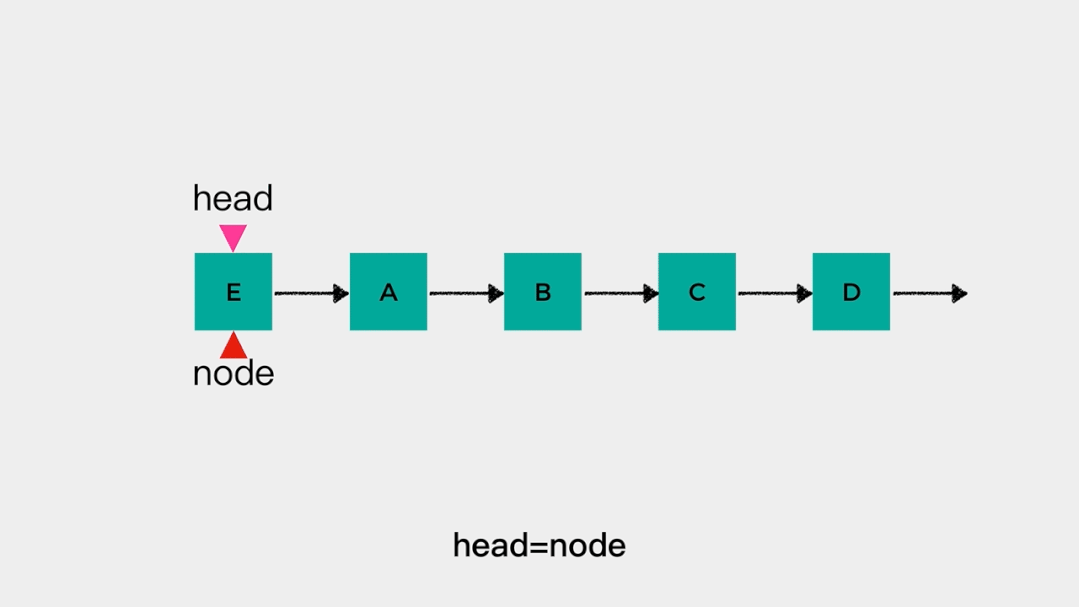：删除链表头节点head时，不需要遍历链表，时间复杂度是O(1)，动画演示如下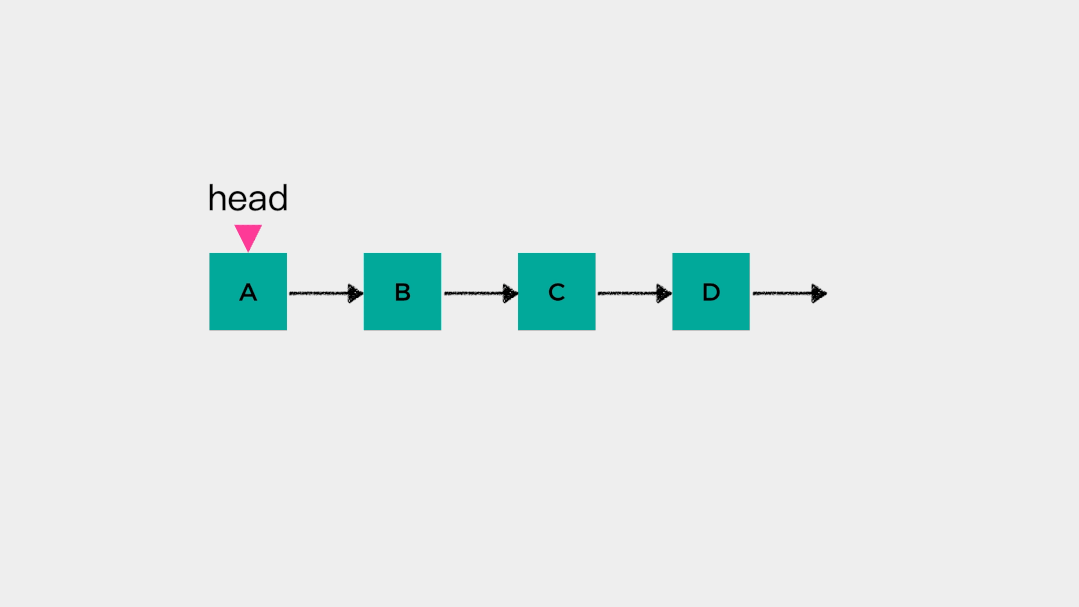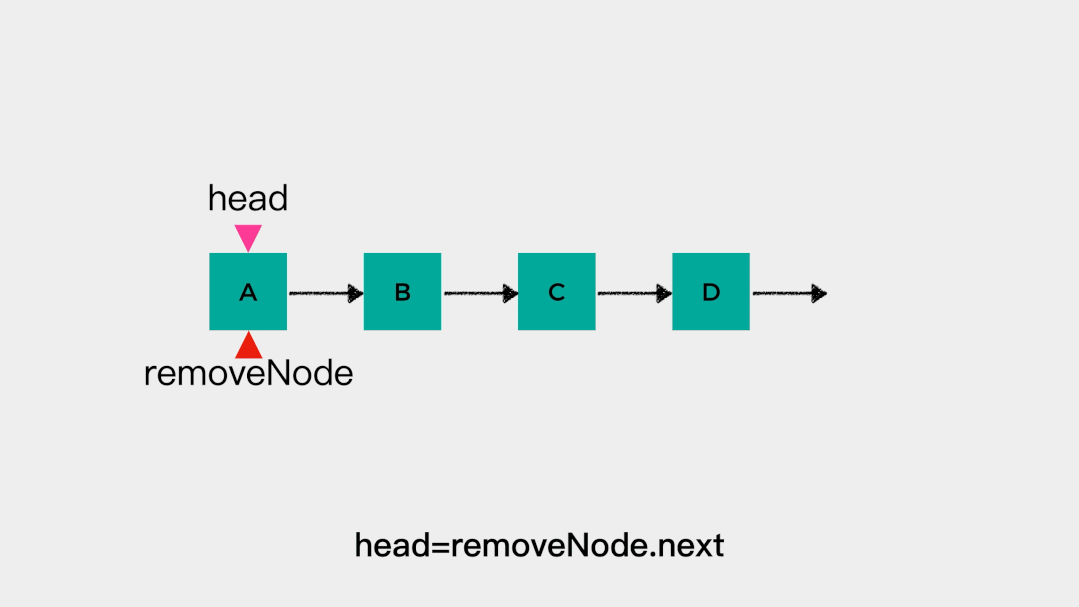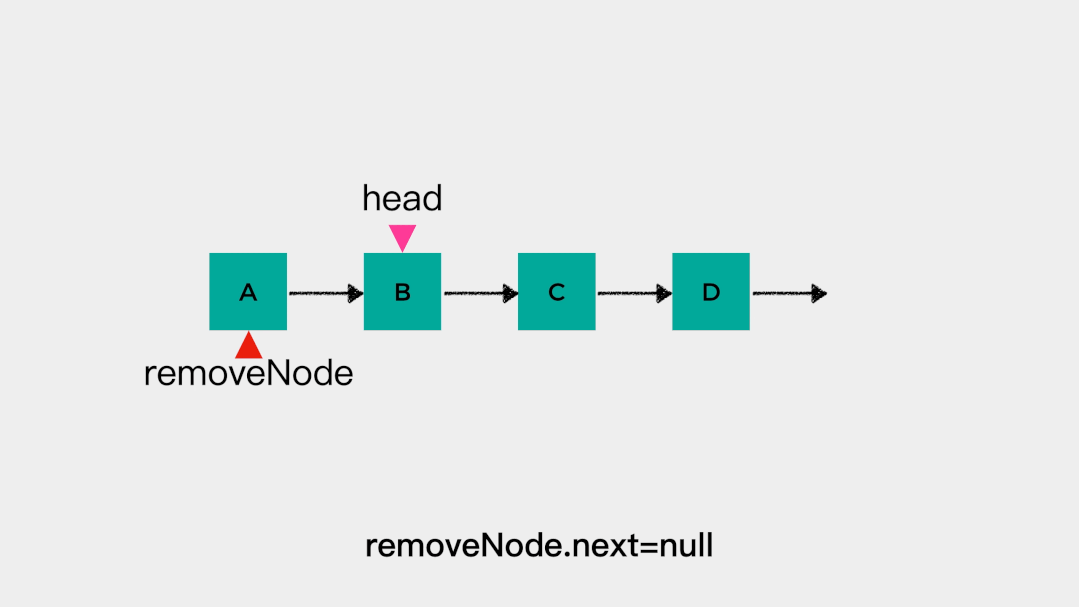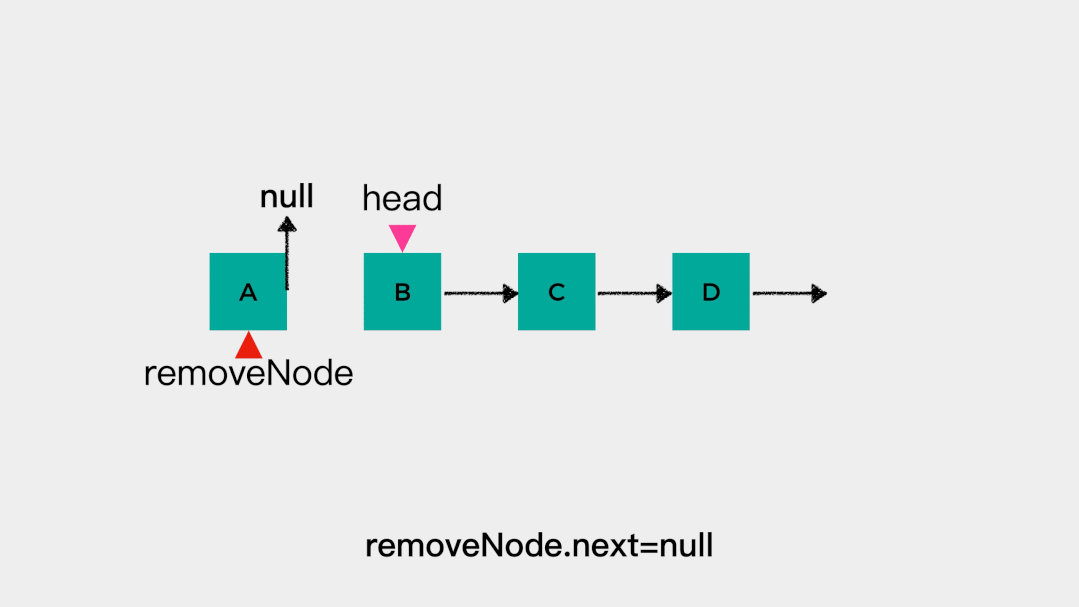：也就是说对于链表的头节点head来说，把其当做队列的队头和队尾都是可以的。但是，队列只允许在一端进行插入操作，在另一端进行删除操作。因此，链表的head这一端，要么做队头，要么做队尾。接着看下当有tail指向链表尾节点时，添加元素和删除元素是怎么样的。向tail所指节点，即链表尾节点添加元素不需要进行遍历操作，时间复杂度是O(1)。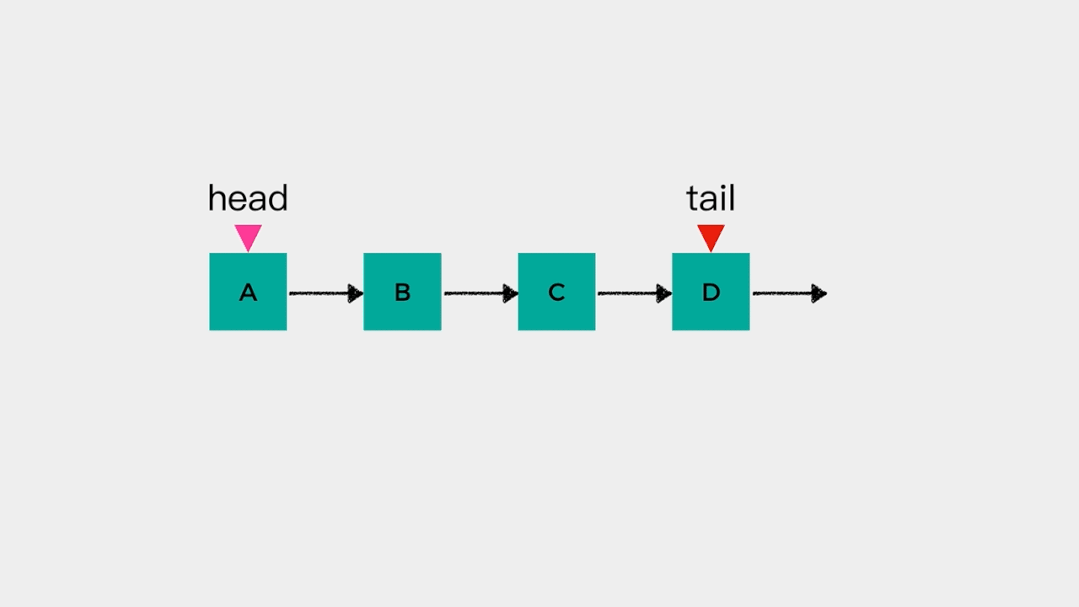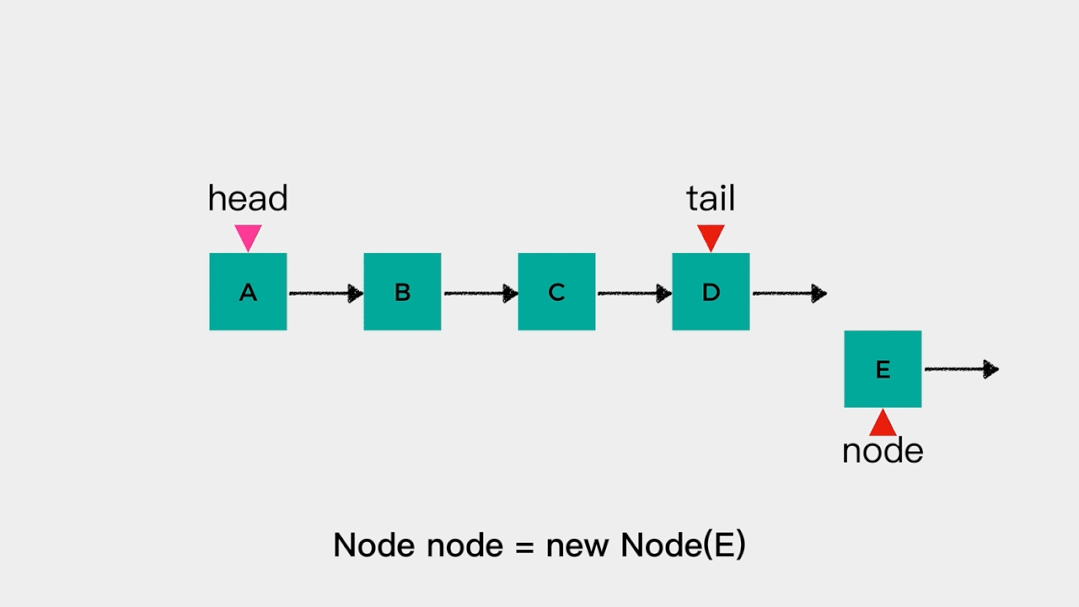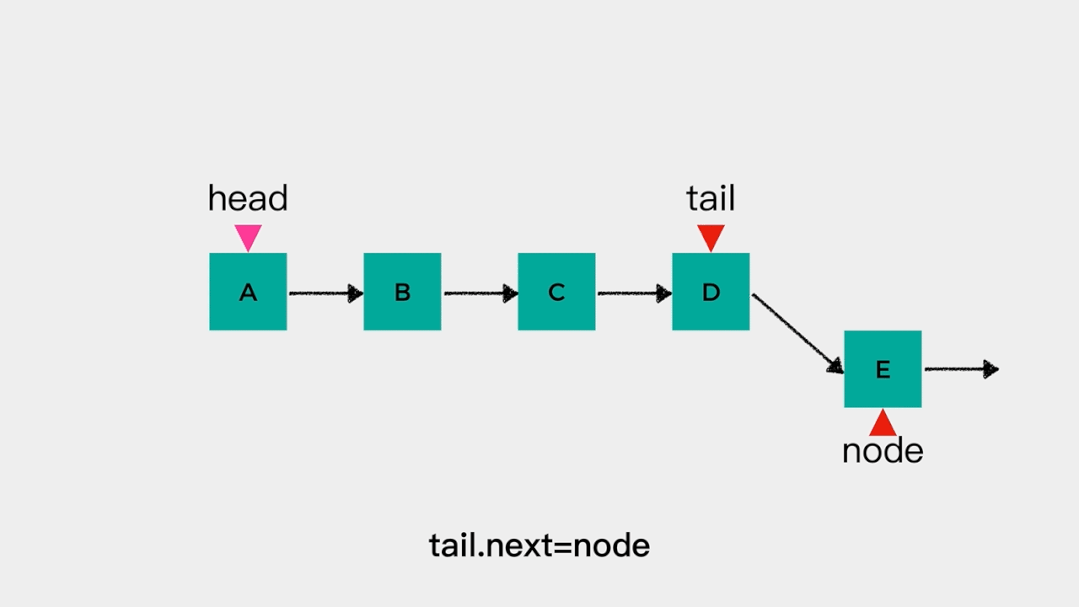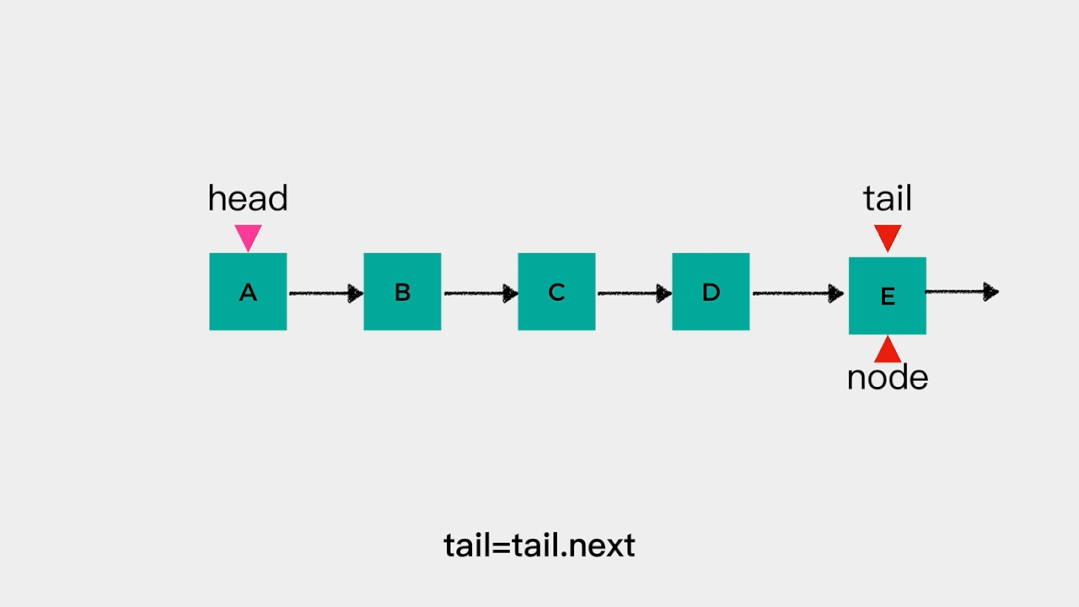在要删除链表尾节点时，要知道tail前一个节点是哪个，就需要从链表头节点开始遍历链表才能确定。因此，如果把链表尾节点当做队列的队头，出队操作的时间复杂度就是O(n)。根据上述分析，应该把head指向的头节点作为队头，tail指向的尾节点作为队尾。这样，出队和入队操作的时间复杂度就都是O(1)。链式队列的代码实现如下：