B 树(查询、插入、删除)

数据结构 B+树

1、简介

B+树是 自平衡树 的一种高级形式，其中所有的值都出现在 叶级 中。
学习B+树之前需要理解的一个重要概念是 多级索引 ( multilevel indexing)。在多级索引中，索引的索引创建如下图所示。它使 访问数据更容易、更快。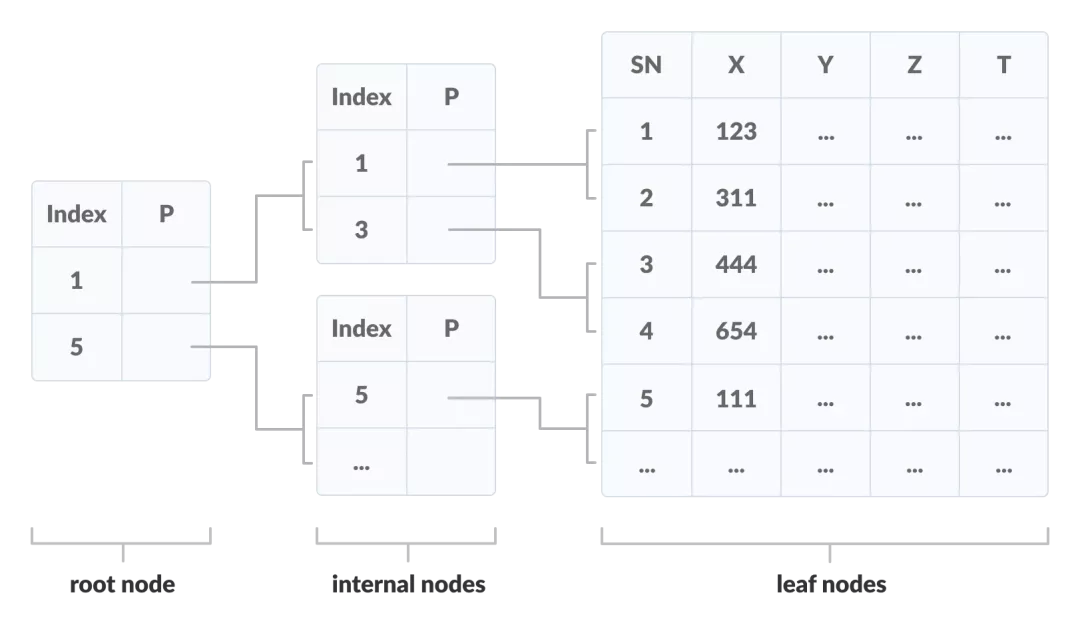

B+树的性质：

1. 所有的 叶子都在同一等级 上。
2. 根 结点至少有 两 个子结点。
3. 除根结点外，每个节点最多可以有m个子节点，且至少有m/2个子节点。
4. 每个节点最多包含m - 1个键，最少包含⌈m/2⌉- 1个键。

B-树和B+树的比较：
B-树：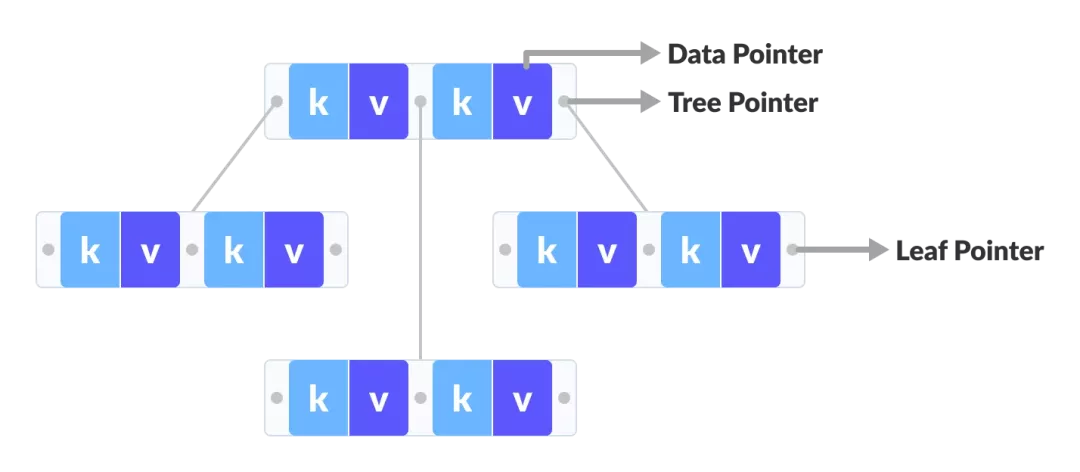

B+树：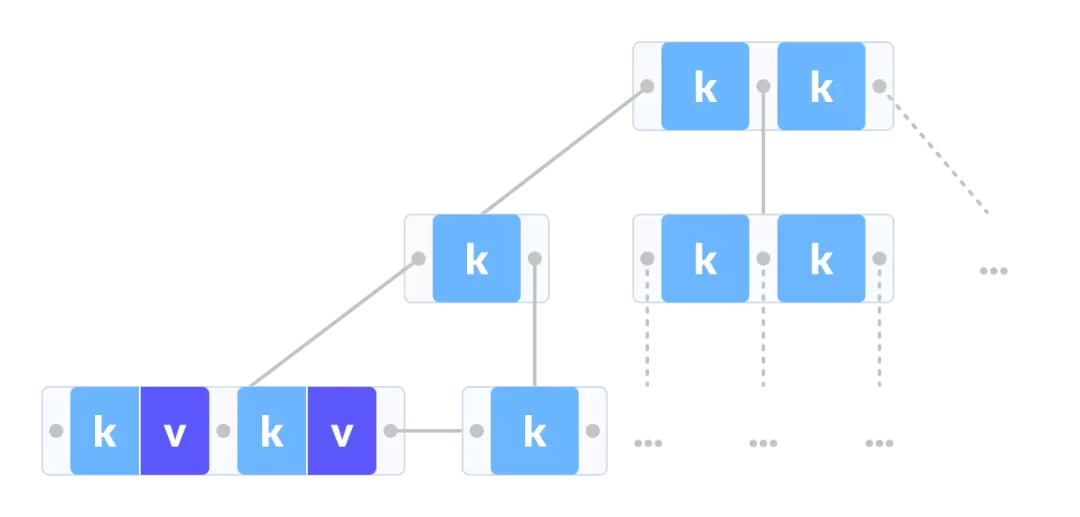

数据指针 只出现在 B+树的叶节点 上，而数据指针出现在 B-树的内部、叶节点或根节点 上。
在 B-树 上，叶结点不是相互连接 的，而在 B+树 上，叶结点是相互连接 的。
在 B+树 上的 操作 比在B-树上的操作要 快。

2、查找

在顺序为m的B+树中搜索数据的步骤如下。设要搜索的数据为k：

1. 从根节点开始。将 k 与根节点 上的键进行比较公里。
2. 如果，到根节点的左子节点。
3. 如果，比较。如果，则 k 在和之间。因此，搜索的左子结点。
4. 如果，去找，和步骤2和步骤3一样。
5. 重复上述步骤，直到到达叶节点。
6. 如果k存在于叶节点中，则返回true，否则返回false。

案例：
在下面的B+树中搜索k = 45。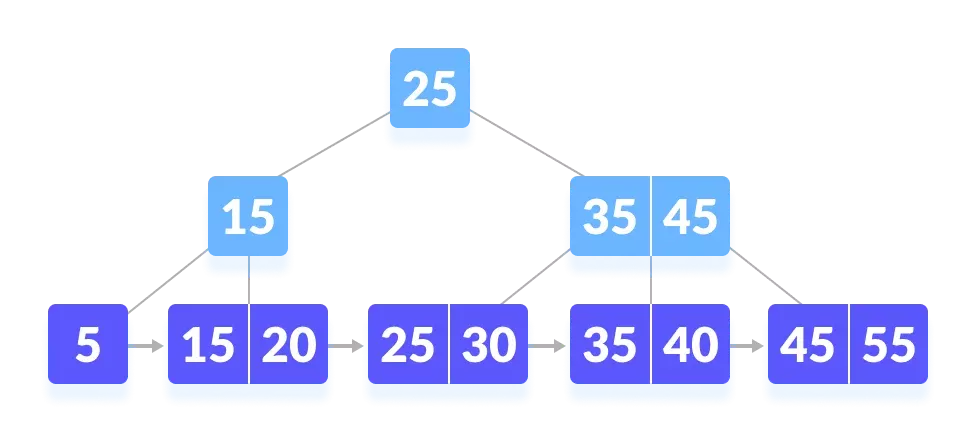

1. 比较 k 和根节点。k 不在根结点上。

1. 因为 k> 25，转到右子结点。
2. 比较 k 和 35。因为 k >30，比较 k 和 45。

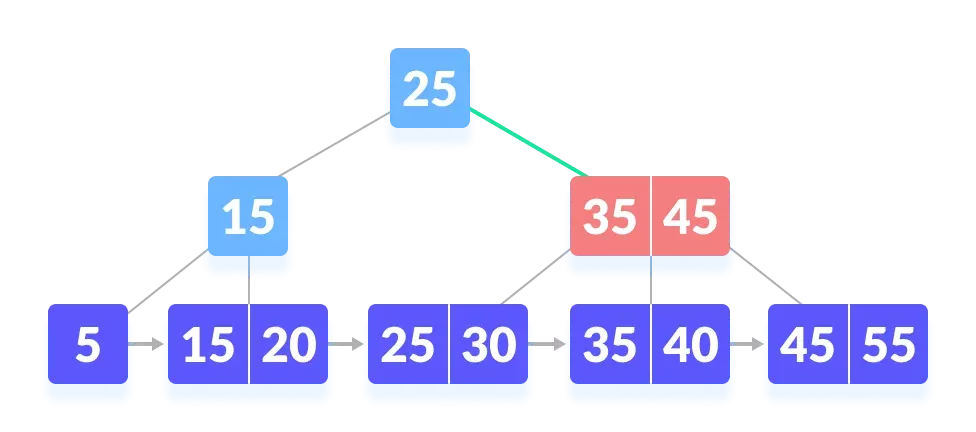
1. 因为 k≥45，所以找右子结点。

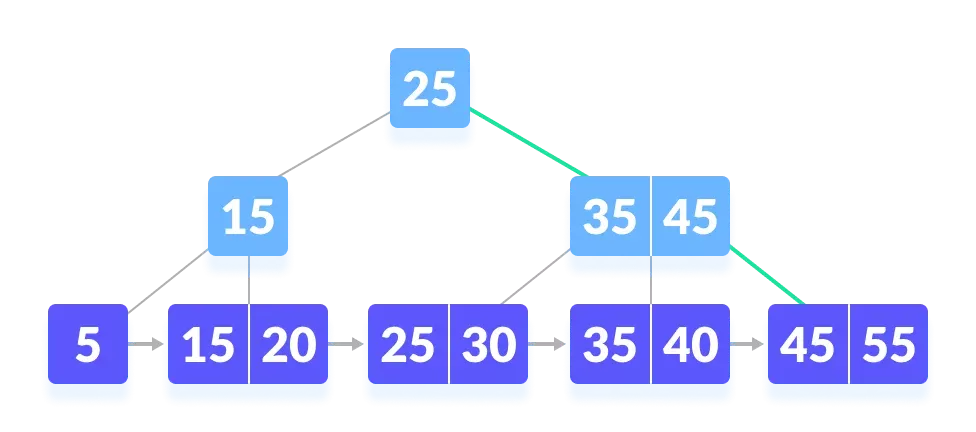
1. k 被找到。

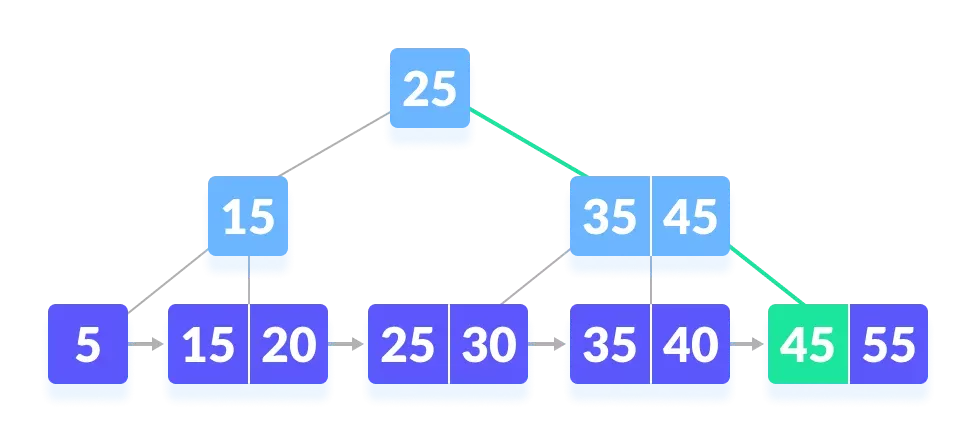
搜索的复杂性：

• 时间复杂度：如果在一个节点内执行线性搜索，那么总复杂度为。如果使用二进制搜索，则总复杂度为。

B +树的应用：

• 多级索引
• 更快的树操作(插入、删除、搜索)
• 数据库索引

  3、插入

  将元素插入B+树包含三个主要事件：搜索 适当的叶子、插入 元素和 平衡/拆分 树。
  按照以下步骤插入元素：

1. 因为每个元素都 插入到叶节点 中，所以转到适当的叶节点。
2. 将键插入叶节点。

case Ⅰ：

• 如果 叶节点未满，则按 递增顺序 将键插入叶节点

case Ⅱ：

1. 如果 叶节点已满，则按递增顺序将键插入叶节点，并按以下方式平衡树。
2. 在m/2位置断开节点。
3. 也向父节点添加 m/2的键。
4. 如果父节点已满，请执行步骤2到步骤3。

案例：
要插入的元素有5、15、25、35、45。

1. 依次插入5、15、25。

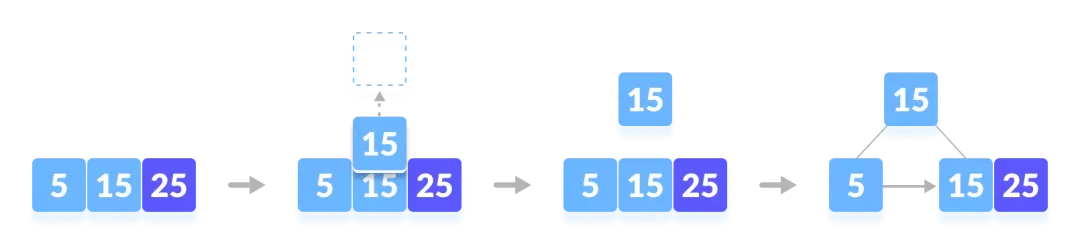
1. 插入35。

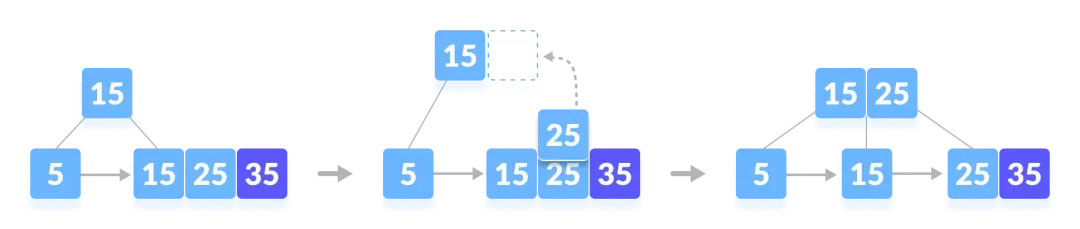
1. 插入45。

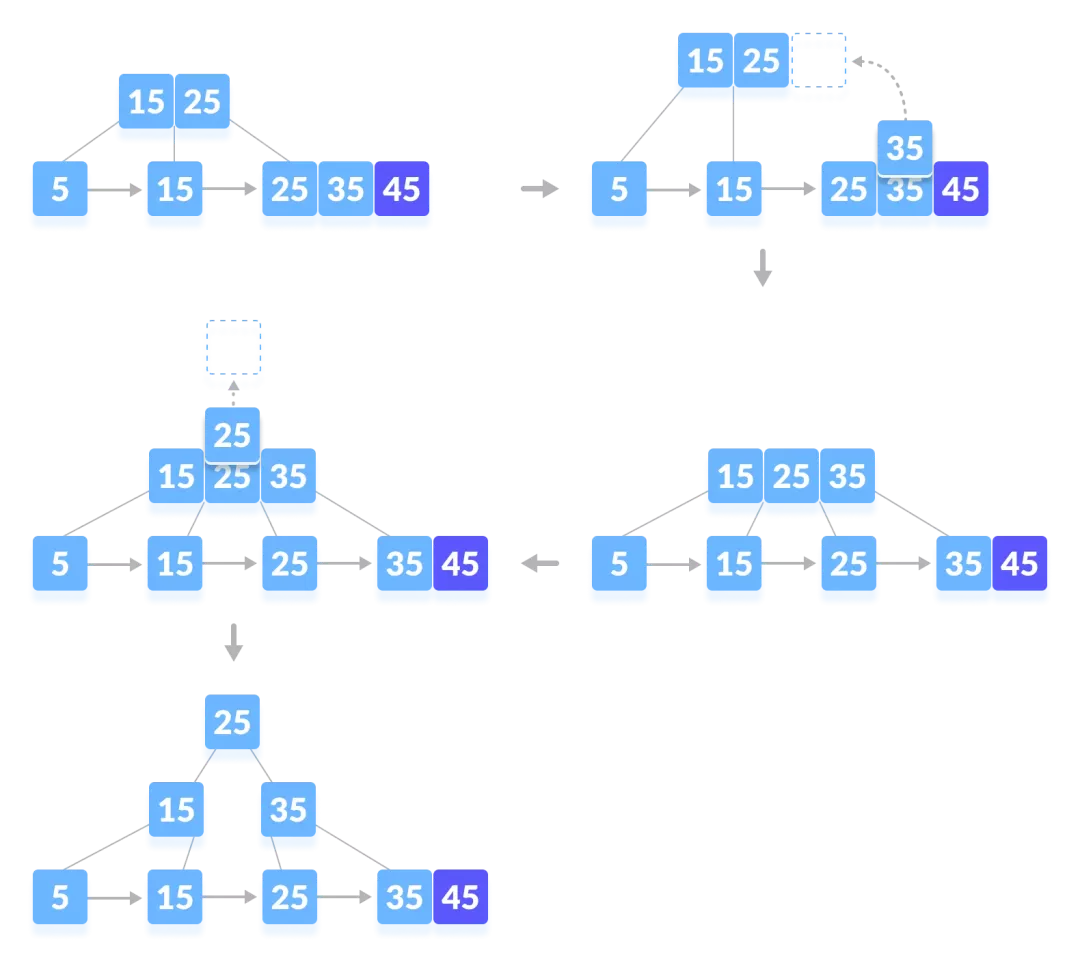
插入的复杂性：

• 时间复杂度：，复杂度由决定

  4、删除

  在B+树中删除一个元素包含三个主要事件：搜索要删除的键所在的节点，删除 键，如果需要的话 平衡 树。
  下溢 是指一个节点中键的数量少于它应该持有的键的最小数量。
  当删除一个键时，我们必须注意内部节点(即索引)中的键，因为值在B+树中是冗余的。搜索要删除的键，然后执行以下步骤。
  case Ⅰ：
  要删除的键只出现在 叶节点 上，而 不在索引 (或内部节点)中。有两种情况：

1. 节点中的键数 超过了最小值。简单地删除键。（删除40）

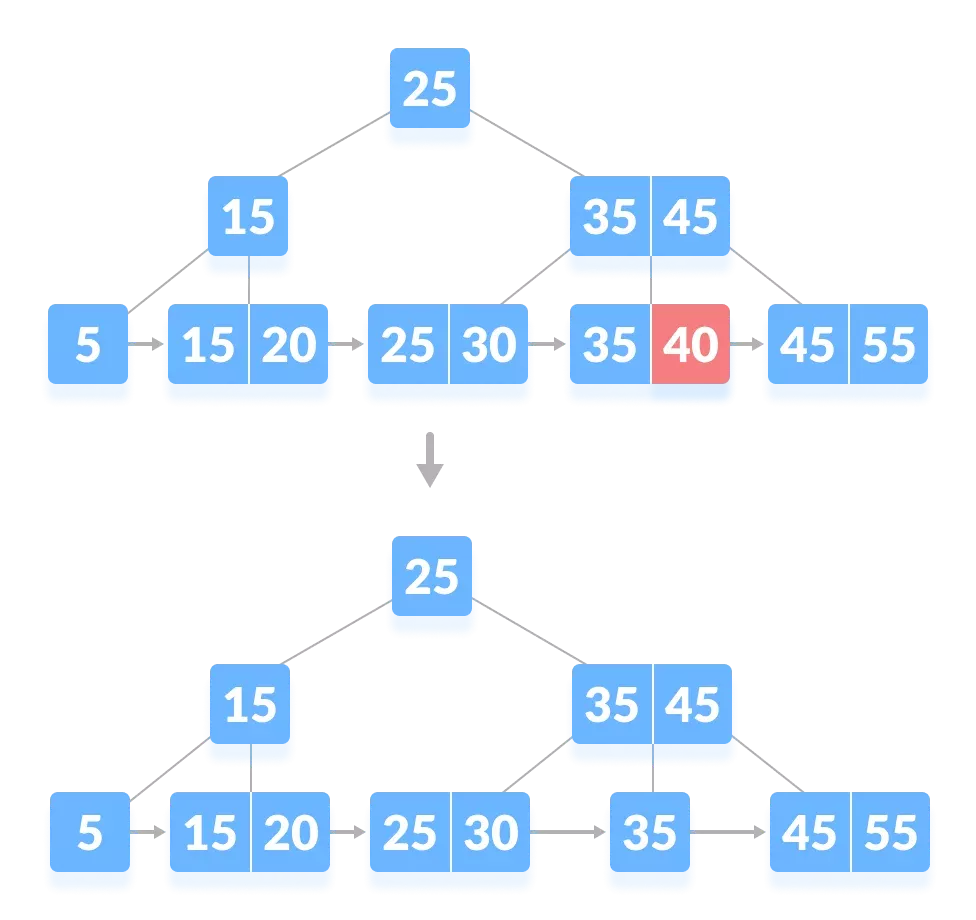
1. 节点中有精确的 最小键数。删除键并从直接的 兄弟节点 借用一个键。将同级节点的 中值键 添加到父节点。（删除5）

case Ⅱ：
要删除的键也存在于 内部节点 中。然后我们也要把它们从内部的结点上移除。对于这种情况，有以下几种情况。

1. 如果节点中键的数量 超过最小值，只需从叶节点中删除该键，并从内部节点中删除该键。

用 中序后继 程序填充内部节点中的空白。（删除45）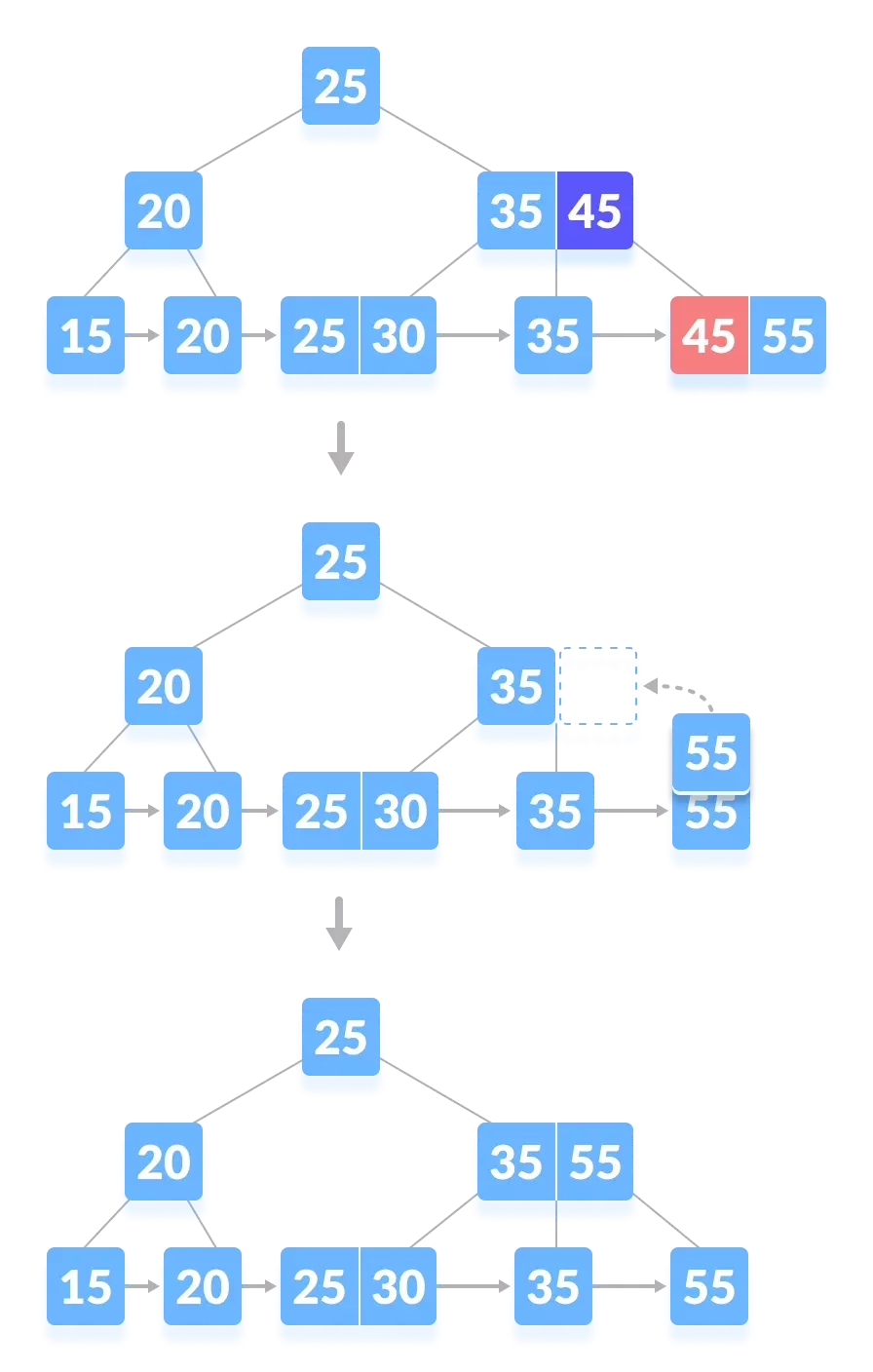

1. 如果节点中有精确的 最小键数，则删除该键，并从其直接 兄弟 节点借用一个键(通过父节点)。

用 借来的键 填充索引(内部节点)中创建的空白。（删除35）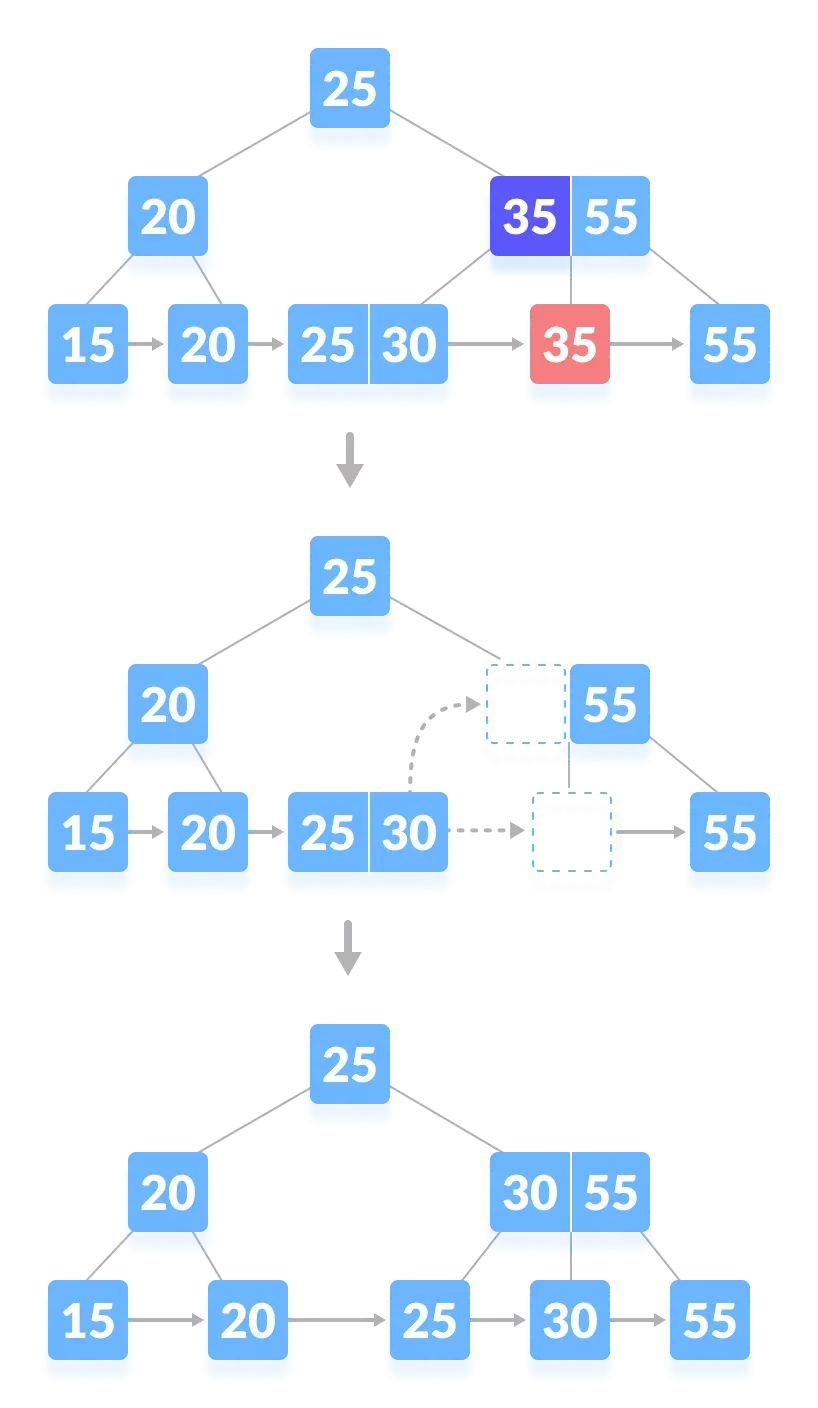

1. 这种情况类似于情形 case II(1)，但在这里，直接 父节点上方生成了空白。

删除键后，将空白空间与其同级空间合并。
用 中序后继 填充祖父节点中的空白。（删除25）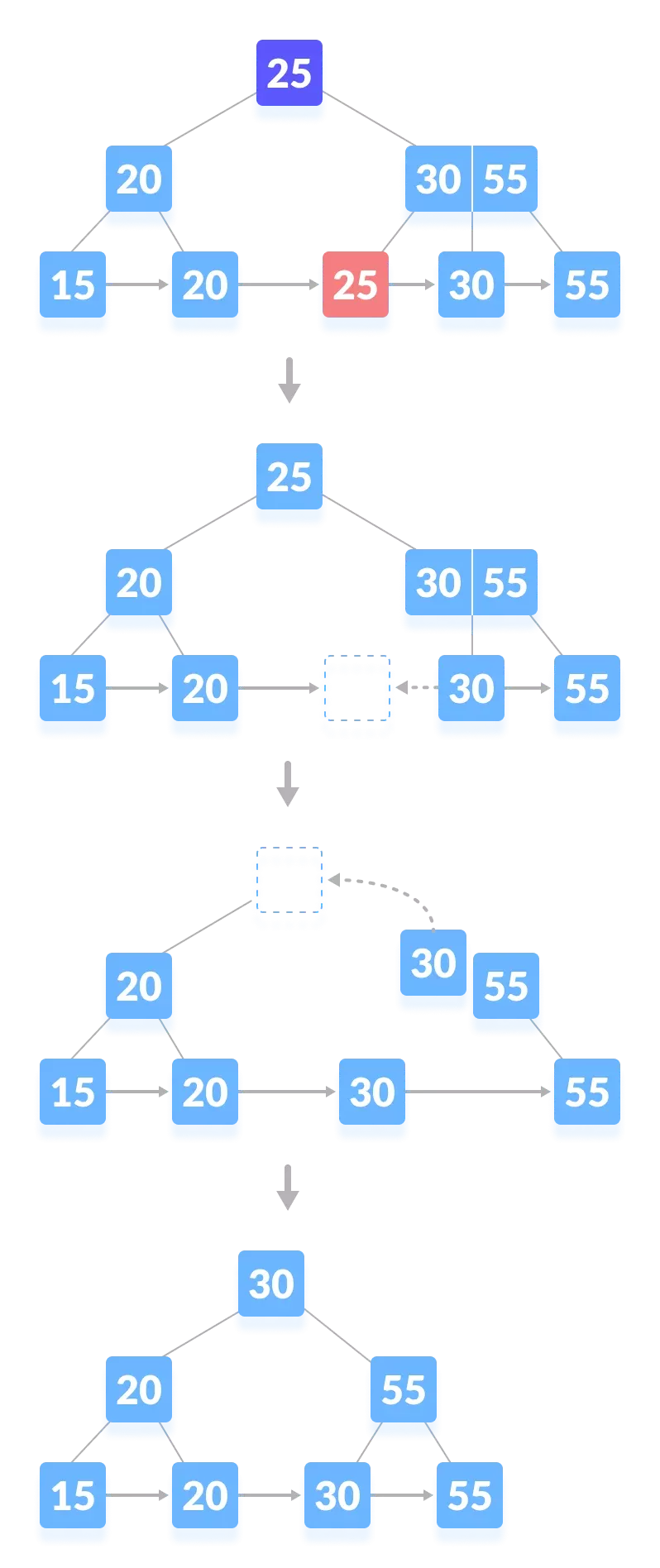

case Ⅲ：
在这种情况下，树的高度会缩小。这有点复杂。从下面的树中 删除55 将导致这种情况。它可以在下面的插图中理解。