主宰这个世界的10大算法 - 几个有趣的算法 - 《算法与数据结构》

根据身份证号码计算出性别、年龄
动态规划
贪心算法

算法

根据身份证号码计算出性别、年龄

一、身份证号码国家标准

1、范围

《公民身份号码》(GB11643-1999)该标准规定了公民身份号码的编码对象、号码的结构和表现形式，使每个编码对象获得一个唯一的、不变的法定号码。

2、号码的结构

公民身份号码是特征组合码，由十七位数字本体码和一位校验码组成。排列顺序从左至右依次为：六位数字地址码，八位数字出生日期码，三位数字顺序码和一位数字校验码。
几个有趣的算法 - 图1
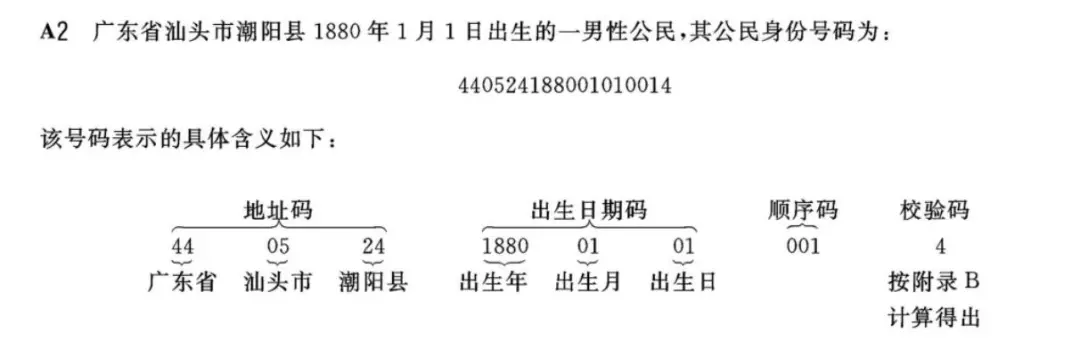
几个有趣的算法 - 图2

2.1、地址码

表示编码对象常住户口所在县(市、旗、区)的行政区划代码

2.2、出生日期码

表示编码对象出生的年、月、日

2.3、顺序码

表示在同一地址码所标识的区域范围内，对同年、同月、同日出生的人编定的顺序号，顺序码的奇数分配给男性，偶数分配给女性。

2.4、校验码

根据前面十七位数字码，按照 ISO 7064:1983.MOD 11-2 中的校验码计算方法计算确定
（1）十七位数字本体码加权求和公式：S = Sum(Ai * Wi)

身份证号	1	1	0	1	0	5	1	9	4	9	1	2	3	1	0	0	2
加权因子	7	9	10	5	8	4	2	1	6	3	7	9	10	5	8	4	2
Ai * Wi	7	9	0	5	0	20	2	9	24	27	7	18	30	5	0	0	4

S = 7 + 9 + 0 + 5 + 0 + 20 + 2 + 9 + 24 + 27 + 7 + 18 + 30 + 5 + 0 + 0 + 4 = 167
（2）计算模：Y = mod(S, 11) Y = 167 % 11 => 2
（3）通过模得到对应的校验码

模	0	1	2	3	4	5	6	7	8	9	10
校验码	1	0	X	9	8	7	6	5	4	3	2

模为 2 时，校验码为 X。

二、代码实现

1、身份证号正确性校验

const WEIGHT = [7,9,10,5,8,4,2,1,6,3,7,9,10,5,8,4,2]
const MO = [1,0,'X',9,8,7,6,5,4,3,2]
function isRightId(id){
  const arr = id.split('')
  const checkNumber = arr.pop() // 去除校验码，将 pop 的返回值赋值给 checkNumber
  let sum = 0
  arr.forEach((ele, index) => {
    sum += ele * WEIGHT[index]
  })
  const m = sum % 11
  const result = MO[m]
  return result+'' === checkNumber
}
console.log(isRightId('11010519491231002X')) // true
console.log(isRightId('110105194912310029')) // false

2、由身份证号计算年龄

function getAge(id){
  // 1、先判断身份证号的正确性
  // 2、判断是否在世
  const year = id.substr(6,4)
  const month = id.substr(10,2)
  const day = id.substr(12,2)
  const timeBrth = new Date(`${year}/${month}/${day}`).getTime()
  const timeNow = new Date().getTime()
  const longTime = timeNow - timeBrth
  const days = longTime / (1*24*60*60*1000)
  let result = ''
  if(days<31){
    result = parseInt(days) + '天'
  }else if(days<365){
    result = `${parseInt(days/30)}月${parseInt(days%30)}天`
  }else{
    result = `${parseInt(days/365)}岁${parseInt(days%365/30)}月${parseInt(days%365%30)}天`
  }
  return result 
}
console.log(getAge('11010519491231002X')) // 71 岁 8 月 16 天
console.log(getAge('11010520210820002X')) // 6 天
console.log(getAge('11010520210720002X')) // 1 月 7 天

3、由身份证号判断性别

function getSex(id){
  // 1、先判断身份证号的正确性
  const sex = id.substr(16,1)
  return sex%2? '男': '女'
}
console.log(getSex('11010519491231002X')) // 女
console.log(getSex('11010520210820001X')) // 男

三、其他

1、变性手术后，身份证号码是否更改？

跨性别人士身份证性别变更后，依户口所在派出所公示为准，进行身份证号码变更。
2、计算年龄前应先确认是否在世。
四、参考资料
《公民身份号码》(GB11643-1999)
动态规划
1、定义
动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。
可以简单的理解为是对传统递归的一种优化。在 DP 的实践中很重要的就是递推关系和边界条件。
2、简单：爬楼梯
题目
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意给定 n 是一个正整数。
示例 1：
``` 输入：2 输出：2 解释：有两种方法可以爬到楼顶。

1 阶 + 1 阶
2 阶
```
<a name="hwcJ6"></a>
#### 示例 2：
```
输入：3 输出：3 解释：有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶 ```
代码：
```javascript // 把数据缓存在一个数组中 var climbStairs = function(n) { let dp = [] dp[0]=1; dp[1]=1; for(let i=2;i<=n;i++){ dp[i]=dp[i-1]+dp[i-2]; } return dp[n]; };

// 使用递归 var climbStairs = function(n) { if(n===1) return 1 if(n===2) return 2 return climbStairs(n-1) + climbStairs(n-2) };

<a name="AIjc2"></a>
#### 思路：
f(x)=f(_x_−1)+f(x_−2) 爬到第 x _级台阶的方案数是爬到第 x - 1 级台阶的方案数和爬到第 x - 2 级台阶的方案数的和。<br />LeetCode 运行结果：![](https://cdn.nlark.com/yuque/0/2021/webp/396745/1634441635242-44ed197c-6c96-4b34-b428-8058ca823307.webp#clientId=uccf3d9ee-64e6-4&from=paste&id=ue2ecfa0c&margin=%5Bobject%20Object%5D&originHeight=161&originWidth=1080&originalType=url&ratio=1&status=done&style=shadow&taskId=u1c8bb2e8-b01e-4b13-b779-44a255b13e0)
<a name="y8wJw"></a>
### 3、中等：最长回文子串
<a name="MEalk"></a>
#### 题目
给你一个字符串 s，找到 s 中最长的回文子串。
<a name="feT51"></a>
#### 示例 1：

输入：s = “babad” 输出：”bab” 解释：”aba” 同样是符合题意的答案。

<a name="or5Dc"></a>
#### 示例 2：

输入：s = “cbbd” 输出：”bb”

<a name="gGHGi"></a>
#### 思路：
当 s[i+1 : j-1]  是回文串，并且 s 的第 i 和 j 个字母相同时，s[i:j]  才会是回文串。<br />即：P(i,j)=P(i+1,j−1) 且 (Si == Sj)。<br />边界条件：子串的长度为 1 或 2。对于长度为 1 的子串，它显然是个回文串；对于长度为 2 的子串，只要它的两个字母相同，它就是一个回文串。

- P(i, i) = true
- P(i, i+1) = (Si == Si+1)
<a name="gI4vU"></a>
#### 代码：
```javascript
function longestPalindrome (s) {
  // 先判断字符串长度，如果为 1 则直接返回
  let len = s.length
  if (len < 2) return s

  // 初始化变量
  let maxLen = 1
  let begin = 0

  // dp[i][j] 表示 s[i..j] 是否是回文串
  let dp = []
  // 初始化：所有长度为 1 的子串都是回文串
  for (let i = 0; i < len; i++) {
    dp[i] = []
    dp[i][i] = true
  }

  // 将字符串切割为数组
  let charArray = s.split('')

  // 递推开始
  for (let L = 2; L <= len; L++) { // 枚举子串长度
    // 枚举左边界，左边界的上限设置可以宽松一些
    for (let i = 0; i < len; i++) {
      // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
      let j = L + i - 1;
      // 如果右边界越界，退出当前循环
      if (j >= len) {
        break;
      }
      // 判断是否为回文
      if (charArray[i] !== charArray[j]) {
        dp[i][j] = false
      } else {
        // 对于一个子串而言，如果它是回文串，并且长度大于 2，那么将它首尾的两个字母去除之后，它仍然是个回文串。
        let flag = j - i < 3
        dp[i][j] = flag ? true : dp[i + 1][j - 1]
      }
      // 当 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，记录回文长度和起始位置
      if (dp[i][j] && j - i + 1 > maxLen) {
        maxLen = j - i + 1;
        begin = i;
      }
    }
  }
  return s.substring(begin, begin + maxLen);
}
console.log(longestPalindrome('babad'), 'babad') // bab babad
console.log(longestPalindrome('cbbd'), 'cbbd') // bb cbbd

LeetCode 运行结果：几个有趣的算法 - 图3

4、困难：接雨水

题目：

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

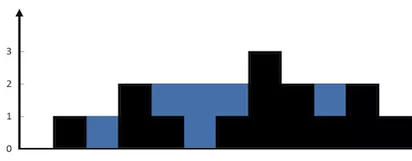
几个有趣的算法 - 图4

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

代码：

function trap(height) {
  // 不满足条件，直接返回
  let len=height.length;
  if(len<=2) return 0;

  let maxLeft = []; // 第 i 根柱子左边最高柱子的高度
  let maxRight = []; // 第 i 根柱子右边最高柱子的高度

  maxLeft[0] = height[0];
  for(let i=1; i<len; i++){
    maxLeft[i] = Math.max(height[i], maxLeft[i-1]) // 动态转移
  }

  maxRight[len-1] = height[len-1];
  for(let j=len-2; j>=0; j--){
    maxRight[j] = Math.max(height[j], maxRight[j+1]) // 动态转移
  }

  let sum=0;
  for(let i=0;i<len;i++) sum+=Math.min(maxLeft[i],maxRight[i])-height[i];

  return sum;
}

思路：

每一列柱子接的雨水是该柱子两侧最高柱子的最小值减去该柱子高度。
LeetCode 运行结果：几个有趣的算法 - 图5

附件：双指针法

代码：

function trap(height) {
  let ans=0;
  for(let i=1; i<height.length-1; i++){
    let l_hight = height[i];
    let r_hight = height[i];

    // 找到 i 列右侧最高柱子高度
    for(let r=i; r<height.length; r++){
      if(height[r]>r_hight) r_hight=height[r];
    }

    // 找到 i 列柱子左侧最高柱子高度
    for(let l=i; l>=0; l--){
      if(height[l]>l_hight) l_hight=height[l];
    }

    ans+=Math.min(l_hight,r_hight)-height[i];
  }
  return ans;
}

LeetCode 运行结果：几个有趣的算法 - 图6

5、参考资料

来源：力扣（LeetCode）
https://leetcode-cn.com/problems/climbing-stairs/
https://leetcode-cn.com/problems/longest-palindromic-substring/
https://leetcode-cn.com/problems/trapping-rain-water/

贪心算法

1、定义

在对问题求解时，总是做出在当前看来是最好的选择。

2、分饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。
示例 1: 输入: g = [1,2,3], s = [1,1] 输出: 1
示例 2: 输入: g = [1,2], s = [1,2,3] 输出: 2

function findContentChildren1(children, cookies){
  children = children.sort((a, b) => a - b)
  cookies = cookies.sort((a, b) => a - b)
  let childrenLength = children.length
  let cookiesLength = cookies.length
  let count = 0
  for(let i = 0, j = 0; i < childrenLength && j < cookiesLength; i++, j++){
    while(j < cookiesLength && children[i] > cookies[j]){
      j++
    }
    if(j < cookiesLength){
      count++
    }
  }
  return count
}


console.log(findContentChildren1([1,2,3], [1,1])) // 1
console.log(findContentChildren1([1,2], [1,2,3])) // 2
console.log(findContentChildren1([1,2,3], [1,1,3,4])) // 3

核心思想：

将孩子的胃口、饼干的大小都按照从小到大排序。
for 循环遍历，比较孩子的胃口 children[i]和饼干的大小 cookies[j]之间的关系，当当前饼干不能满足孩子的胃口时，选择下一个饼干进行比较。
如果满足孩子的胃口，且 j 在范围内，则 count 加 1。

代码解读：
定义函数 findContentChildren，接受 2 个参数，分别为 children：孩子的胃口，cookies 饼干的大小。
将 children 和 cookies 按照从小到大排序。
定义能够满足孩子胃口的个数 count，并最终将 count 返回。
循环遍历，当 children[i] > cookies[j] 即当前饼干不能满足孩子时，j++选择下一块饼干进行比较。
如果 children[i] <= cookies[j] 即当前饼干能满足孩子，且 j 在范围内，则 count 加 1。
进入下一次循环（即尝试满足下一个孩子）。
3、买股票
给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格；整数 fee 代表了交易股票的手续费用。你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。返回获得利润的最大值。注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。
示例 1：输入：prices = [1, 3, 2, 8, 4, 9]， fee = 2，输出：8
解释：
能够达到的最大利润:
在此处买入 prices[0] = 1 在此处卖出 prices[3] = 8 在此处买入 prices[4] = 4 在此处卖出 prices[5] = 9 总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8
示例 2：输入：prices = [1,3,7,5,10,3], fee = 3 输出：6 ```javascript function maxProfit(list, fee){ const length = list.length let buy = list[0] + fee // 假定：买入时机为第 1 天 let profit = 0 for(let i = 1; i < length; i++){ if(list[i]+fee < buy){ // 如果股票价格降低，则调整买入时机 buy = list[i]+fee }else if(list[i] > buy){ // 如果有利润，则卖出 profit += list[i] - buy // 计算利润 buy = list[i] // 调整买入时机 } } return profit }

console.log(maxProfit([1, 3, 2, 8, 4, 9], 2)) // 8 console.log(maxProfit([1,3,7,5,10,3], 3)) // 6

<a name="sK2Ws"></a>
#### 代码解读：

1. 定义函数 maxProfit，接受 2 个参数，list 为股票价格趋势，fee 为手续费
1. 定义 profit，并在最后将 profit 返回
1. 假定：买入时机为第 1 天（即：list[0]）
1. 如果股票价格降低，则调整买入时机为后一天
1. 如果有利润，则卖出，并计算利润，再次调整买入时机（即循环步骤 3、4、5）
<a name="eK2Ts"></a>
#### 核心思想：

1. 假定：买入时机为第 1 天
1. 如果股票价格降低，则调整买入时机为后一天
1. 如果有利润，则卖出，并且计算利润
1. 再次 - 假定：买入时机（循环步骤 1-3）
<a name="NNsAw"></a>
### 4、情侣牵手
N 对情侣坐在连续排列的 2N 个座位上，想要牵到对方的手。计算最少交换座位的次数，以便每对情侣可以并肩坐在一起。一次交换可选择任意两人，让他们站起来交换座位。人和座位用 0 到 2N-1 的整数表示，情侣们按顺序编号，第一对是 (0, 1)，第二对是 (2, 3)，以此类推，最后一对是 (2N-2, 2N-1)。<br />这些情侣的初始座位  row[i] 是由最初始坐在第 i 个座位上的人决定的。
<a name="l6zq2"></a>
#### 示例 1:
输入: row = [0, 2, 1, 3] 输出: 1 <br />解释: 只需要交换 row[1]和 row[2]的位置即可。
<a name="tPr13"></a>
#### 示例 2:
输入: row = [3, 2, 0, 1] 输出: 0 解释: 无需交换座位，所有的情侣都已经可以手牵手了。
```javascript
/**
 * @param {number[]} row
 * @return {number}
 */
var minSwapsCouples = function(row) {
    let hashMap = {}; // {人: 位置}
    for(let i=0; i<row.length; i++){
      hashMap[row[i]] = i
    }

    let ans = 0; // 交换次数

    for(let i=0; i<row.length; i+=2){ // 按照一对遍历
        let lover=row[i]^1; // row[i]的情侣
        if(hashMap[lover] !== i+1){ // 如果不相邻，就交换
            ans++;
            hashMap[row[i+1]] = hashMap[lover]; // row[i+1]使用了 lover 的下标
             // 交换位置
            [row[i+1], row[hashMap[lover]]] = [row[hashMap[lover]], row[i+1]]
            hashMap[lover]=i+1; // lover 的下标改为 i+1 使其相邻
        }
    }
    return ans;
};

核心思想：

遍历数组，检查情侣是否相邻，如果不是，就调整一个的位置使其相邻。
尽量只挪动情侣中的一位，另一位不动，这样才能保证挪动次数最少。
这样交换，不会影响其他的情侣。

代码解读：
定义函数 minSwapsCouples，接收一个参数 row 即情侣座位关系的数组。
得到{人: 位置}的对象。
定义交换次数 ans，并在最后将其返回。
遍历左侧情侣，检查右侧是否为 TA 的情侣，如果不是，则找到 TA 的情侣并调换座位。

几个有趣的算法

根据身份证号码计算出性别、年龄

一、身份证号码国家标准

1、范围

2、号码的结构

2.1、地址码

2.2、出生日期码

2.3、顺序码

2.4、校验码

二、代码实现

1、身份证号正确性校验

2、由身份证号计算年龄

3、由身份证号判断性别

三、其他

1、变性手术后，身份证号码是否更改？

2、计算年龄前应先确认是否在世。

四、参考资料

动态规划

1、定义

2、简单：爬楼梯

题目

示例 1：

代码：

4、困难：接雨水

题目：

示例 1：

示例 2：

代码：

思路：

附件：双指针法

5、参考资料

贪心算法

1、定义

2、分饼干

核心思想：

代码解读：

3、买股票

核心思想：

代码解读：