一、 二分查找

前提条件： 原来的数列是有序的。

1. 时间复杂度

O(log2n)

2. 代码实现

1. 非递归

// 非递归实现
    /**
     *
     * @param arr 待查找的数组
     * @param target 目标树字
     * @return -1表示没找到，否则返回下标
     */
    public static int binarySearch(int[] arr, int target){
        int left = 0;
        int right = arr.length-1;
        while (left<=right){
            int mid = (left+right)/2;
            if(arr[mid]==target){
                return mid;
            }else if(arr[mid]>target){
                // 在左子数组种
                right=mid-1;
            }else {
                left=mid+1;
            }
        }
        return -1;
    }

2. 递归实现

public static int binarySearchRecur(int[] arr,int left,int right, int target){
        int mid=(left+right)/2;
        if(arr[mid]==target){
            return mid;
        }
        if(left>=right){
            return -1;
        }else if(arr[mid]<target){
            return binarySearchRecur(arr, mid+1, right, target);
        }else if(arr[mid]>target){
            return binarySearchRecur(arr, left, mid-1, target);
        }
        return -1;
    }

二、分治算法

二分法是分治算法的一种体现
基本原理： 把一个复杂的问题，分解成多个相同或相似的子问题，再把各个子问题进一步分解。最后合并众多子问题。
核心问题： 拆解

1. 分治算法实现步骤

2. 实例：汉诺塔

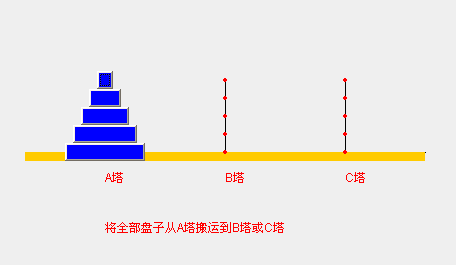
参考链接：https://www.zhihu.com/question/37152936/answer/728940730

作者：制约与平衡
链接：https://www.zhihu.com/question/37152936/answer/728940730
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

/**
     * @param num 盘的个数
     * @param a   第一个柱子参数： 起始位置
     * @param b   第二个柱子参数： 过度位置
     * @param c   第三个柱子参数： 终点位置
     */
    public static void hanoitower(int num, char a, char b, char c) {
        // 如果只有一个盘
        if (num == 1) {
            System.out.println("第1个盘移动：" + a + "-->" + c);
        } else {
            // 如果大于等于2个盘
            // step1: 把除最下面的盘外的其他所有盘从a-->b, 中间会使用到c
            // 三个位置参数： 第一个是起始位置，第二个是过度位置，第三个是终点位置
            hanoitower(num - 1, a, c, b);
            // step2:把最下面的盘从b移动到c,移动过程中会用到a
            hanoitower(num-1, b, a, c);
        }
    }

三、动态规划

1. 核心思想

将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法。

2. 分治算法 vs 动态规划

分治算法： 从小到大进行递归合并
动态规划： 从大到小进行划分 求解

动态规划算法与分治算法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解 )

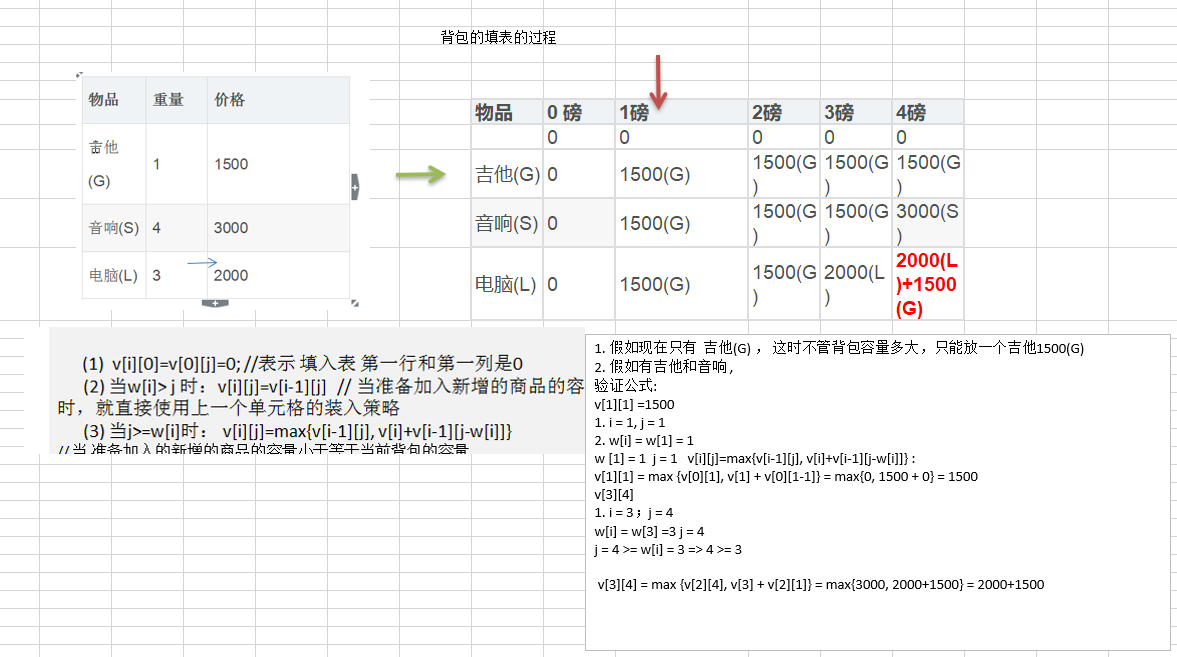
注意：最后一行的意思是： 当当前的容量大于最大价值物品的容量时，放入该最大价值物品，然后在剩余容量内选择最大价值物品。
整体逻辑： 从小到大，选出每个方框最大容量对应的最大价值； 当容量增加后，优化选择更大的容量价值。