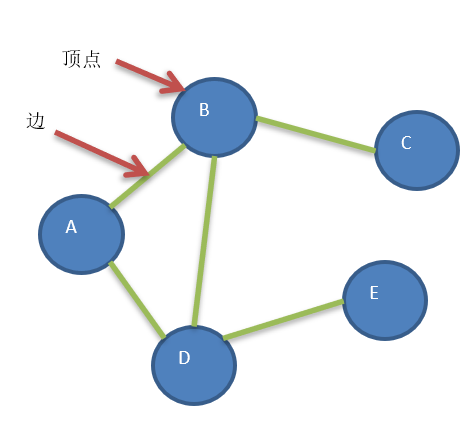
一、图

1. 图的存在意义

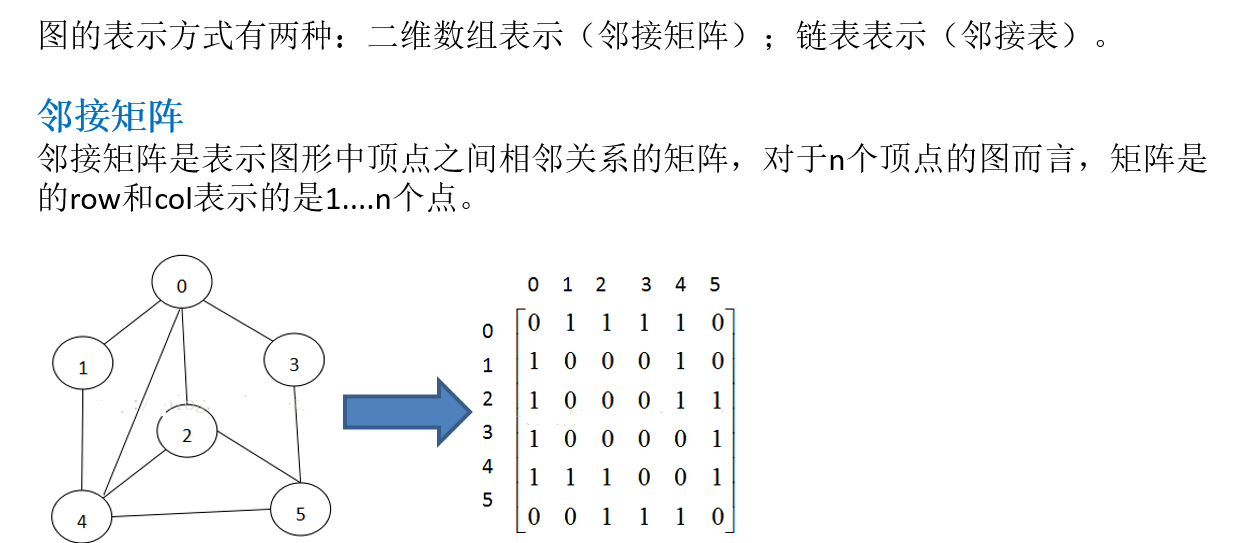
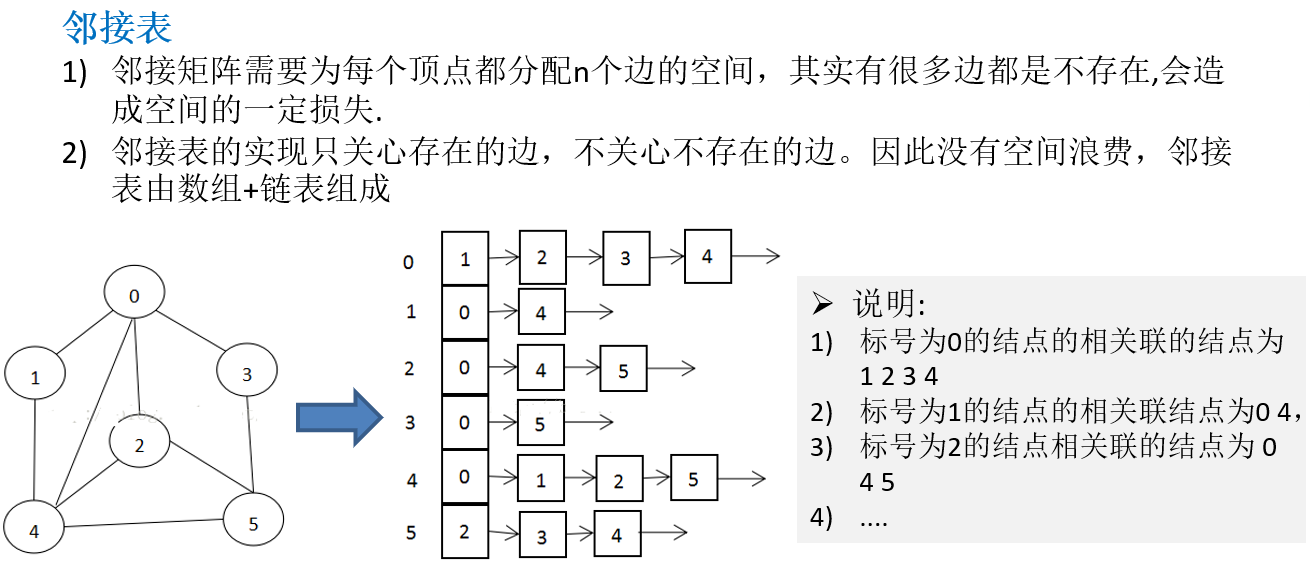
2. 图的表示方式

3. 代码实现

step1: ArrayList vertexList; //存储顶点集合
step2: int[][] 二维矩阵存储关系
step3: int numberOfEdges; //边的数目

import java.util.ArrayList;
import java.util.Arrays;
public class GraphDemo {
    private ArrayList<String> vertexList; //存储顶点集合
    private int[][] edges;// 存储图对应的零阶矩阵
    private int numberOfEdges; //边的数目
    public static void main(String[] args) {
        int n=5;
        String[] vertexValue = {"a","b","c","d","e"};
        // 创建图对象
        GraphDemo graph = new GraphDemo(5);
        for (String vertex : vertexValue) {
            graph.insertVertex(vertex);
        }
        // 添加边
        graph.insertEdge(0, 1, 1);
        graph.insertEdge(0, 2, 1);
        graph.insertEdge(1, 2, 1);
        graph.insertEdge(1, 3, 1);
        graph.insertEdge(1, 4, 1);
        graph.showGraph();
    }
    /**
     *
     * @param n 矩阵的维度
     */
    public GraphDemo(int n) {
        // 初始化矩阵和arrayList
        edges = new int[n][n];
        vertexList= new ArrayList<String>(n);  // 放N个数据进去
        numberOfEdges=0;
    }
    // 返回节点的个数
    public int getNumberOfVertex(){
        return vertexList.size();
    }
    // 得到边的数目
    public int getNumberOfEdges(){
        return numberOfEdges;
    }
    // 返回节点下标为i的点对应的数据
    public String getValueByVertexIndex(int i){
        return vertexList.get(i);
    }
    // 显示图的矩阵--》遍历二维数组
    public void showGraph(){
        for(int[] link:edges){
            System.out.println(Arrays.toString(link));
        }
    }
    // 返回v1和v2的权值
    public int getWeight(int v1, int v2){
        return edges[v1][v2];
    }
    /**
     *
     * @param vertex 插入顶点，其名称为vertex
     */
    public void insertVertex(String vertex){
        vertexList.add(vertex);
    }
    /**
     *
     * @param v1 表示点的下标，即第几个顶点，顶点的下标
     * @param v2 表示点的下标，即第几个顶点，顶点的下标
     * @param weight 点之间的权值
     */
    public void insertEdge(int v1, int v2, int weight){
        edges[v1][v2]=weight;
        edges[v2][v1]=weight;
        numberOfEdges++;
    }
}

4. 图的深度优先算法（DFS）

1. 过程解析

2. 代码解析

step1: 获取第一个邻接节点—-即当前行的第一个元素

/**
     *
     * @param index 在二维数组中的行号， j代表的是二维数组中的列号
     * @return 当前行的第多少列
     */
    public int getFirstNeighbor(int index){
        for(int j=0;j<vertexList.size();j++){
            if(edges[index][j]>0){
                return j;
            }
        }
        return -1;
    }

step2: 获取当前行当前元素的下一个邻接节点

// 根据前一个邻接节点的下标，获取下一个邻接节点
    public int getNextNeighbor(int v1,int v2){
        for(int j=v2+1;j<vertexList.size();j++){
            if(edges[v1][j]>0){
                return j;
            }
        }
        return -1;
    }

step3: 深度遍历

/**
     * 传进来的是二维数组的行
     * @param isVisted 如果已经访问过，则加入到该链表中
     * @param i 节点的下标,即二维数组中的行
     */
    public void dfs(boolean[] isVisted, int i){
        System.out.printf("当前第%s个节点已经被访问", i);
        isVisted[i]=true;
        // 已当前节点i的第一个邻接节点w
        int w = getFirstNeighbor(i);  // 还是第I行，w列
        while(w!=-1){
            // 有邻接节点
            if(!isVisted[w]){
                // 没有访问就可以正常访问
                dfs(isVisted, w);
            }
            w=getNextNeighbor(i, w);
        }
    }
    // 对dfs进行重载，遍历所有的节点并进行dfs
    public void dfs(){
        for (int i = 0; i < getNumberOfVertex(); i++) {
            if(!isVisted[i]){
                dfs(isVisted, i);
            }
        }
    }

5. 广度优先遍历（BFS）