特征选择和特征降维我们可以把他们统称为特征工程。两者区别是：特征选择不产生新的特征，通过一些手段来筛选特征；特征降维会产生新的特征，高维空间映射到低维空间，如对已有特征做线性组合。
严格上说特征选择属于特征降维，因为维度少了嘛，为了方便讲解，以是否产生新的特征把它们分开。首先要回答为什么要做特征工程？

  1. 特征之间可能存在冗余，高度线性相关，此时容易导致模型过拟合
  2. 特征降维可以解决“维度灾难”，以最简单的K近邻算法为例，高维空间会给距离计算带来很大麻烦：计算时间复杂度高，样本稀疏。

特征降维本质是度量学习，也就是找到一个合适的样本空间，使得在这个空间下模型取得好效果，像分类任务，同类样本距离小，不同类样本间距离大，这就是一个合适的样本空间，有监督降维—线性判别分析正是这样的思想。CV中的人脸识别、NLP中的word2vec都有度量学习的身影！

特征降维分为：无监督，以PCA主成分分析为首；有监督，以线性判别分析为首。
PCA：高维样本点到低维空间的距离足够近；样板点在这个低维空间尽可能分开。
线性判别分析：类间距离大，类内距离小。

PCA和特征选择技术都是特征工程的一部分，它们有什么不同？

特征选择是从已存在的特征中选取携带信息最多的，选完之后的特征依然具有可解释性，我们依然知道这个特征在原数据的哪个位置，代表着原数据上的什么含义。而PCA，是将已存在的特征进行压缩，降维完毕后的特征不是原本的特征矩阵中的任何一个特征，而是通过某些方式组合起来的新特征。通常来说，在新的特征矩阵生成之前，我们无法知晓PCA都建立了怎样的新特征向量，新特征矩阵生成之后也不具有可读性，我们无法判断新特征矩阵的特征是从原数据中的什么特征组合而来，新特征虽然带有原始数据的信息，却已经不是原数据上代表着的含义了。以PCA为代表的降维算法因此是特征创造（feature creation，或feature construction）的一种。
可以想见，PCA一般不适用于探索特征和标签之间的关系的模型（如线性回归），因为无法解释的新特征和标签之间的关系不具有意义。在线性回归模型中，我们使用特征选择。

以下内容参考文章 https://www.cnblogs.com/wj-1314/p/10144700.html

一，PCA 的目的

PCA算法是一种在尽可能减少信息损失的前提下，找到某种方式降低数据的维度的方法。PCA通常用于高维数据集的探索与可视化，还可以用于数据压缩，数据预处理。
通常来说，我们期望得到的结果，是把原始数据的特征空间（n个d维样本）投影到一个小一点的子空间里去，并尽可能表达的很好（就是损失信息最少）。常见的应用在于模式识别中，我们可以通过减少特征空间的维度，抽取子空间的数据来最好的表达我们的数据，从而减少参数估计的误差。注意，主成分分析通常会得到协方差矩阵和相关矩阵。这些矩阵可以通过原始数据计算出来。协方差矩阵包含平方和向量积的和。相关矩阵与协方差矩阵类似，但是第一个变量，也就是第一列，是标准化后的数据。如果变量之间的方差很大，或者变量的量纲不统一，我们必须先标准化再进行主成分分析。

二，PCA算法思路

  1. 去掉数据的类别特征（label），将去掉后的 d 维数据作为样本
  2. 计算 d 维的均值向量（即所有数据的每一维向量的均值）
  3. 计算所有数据的散布矩阵（或者协方差矩阵）
  4. 计算特征值（e1 , e2 , e3 , …. ed）以及相应的特征向量（lambda1，lambda2，…lambda d）
  5. 按照特征值的大小对特征向量降序排序，选择前 k 个最大的特征向量，组成 d*k 维的矩阵W（其中每一列代表一个特征向量）
  6. 运行 d*K 的特征向量矩阵W将样本数据变换成新的子空间。
    • 注意1：虽然PCA有降维的效果，也许对避免过拟合有作用，但是最好不要用PCA去作用于过拟合。
    • 注意2：在训练集中找出PCA的主成分，（可以看做为映射mapping），然后应用到测试集和交叉验证集中，而不是对所有数据集使用PCA然后再划分训练集，测试集和交叉验证集。

      三，PCA算法流程

      下面我们看看具体的算法流程：
      输入：n维样本集 D=(x1, x2, … xm)，要降维到的维数 n’。
      输出：降维后的样本集D’
      1） 对有所的样本进行中心化：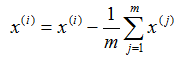
      个人理解 - 图1
      2） 计算样本的协方差矩阵XXT
      3） 对矩阵 XXT 进行特征值分解
      4） 取出最大的 n’ 个特征值对应的特征向量 （w1, w2, …wn），将所有的特征向量标准化后，组成特征向量矩阵W。
      5） 对样本集中的每一个样本 xi，转化为新的样本 Zi = wTXi
      6） 得到输出的样本集 D ‘ =(z1, z2, … zm)

有时候，我们不指定降维后的 n’ 的值，而是换种方式，指定一个降维到的主成分比重阈值 t 。这个阈值 t 在 (0 , 1]之间。加入我们的 n个特征值为λ1>=λ2>=…λn，则 n’ 可以通过下式得到：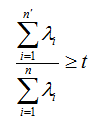
个人理解 - 图2

四，PCA算法优缺点总结

PCA算法作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。为了克服PCA的一些缺点，出现了很多PCA的变种，比如未解决非线性降维的KPCA，还有解决内存限制的增量PCA方法Incremental PCA ，以及解决稀疏数据降维的PCA方法Sparse PCA 等等。

4.1 PCA算法优点

  • 1，仅仅需要以方差衡量信息量，不受数据集以外的因素影响
  • 2，各主成分之间正交，可消除原始数据成分间的相互影响的因素

  • 3，计算方法简单，主要运算时特征值分解，易于实现

    4.2 PCA算法缺点

  • 1，主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强

  • 2，方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。