混淆矩阵的定义
混淆矩阵(Confusion Matrix),它的本质远没有它的名字听上去那么拉风。矩阵,可以理解为就是一张表格,混淆矩阵其实就是一张表格而已。以分类模型中最简单的二分类为例,对于这种问题,我们的模型最终需要判断样本的结果是0还是1,或者说是positive还是negative。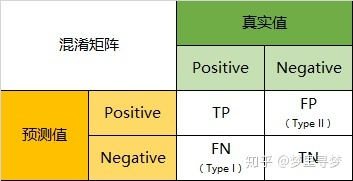
- TP: 将正类预测为正类数;TN: 将负类预测为负类数;
- FP: 将负类预测为正类数(错报);FN: 将正类预测为负类数(漏报)。
此前一直要记混这4个词的含义,实际应该这么来记:
TP为例,意思是预测为P,即正类,结果为T,即正确,那么这个物体就真的为正类;
FN为例,意思是预测为N,即负类,结果为F,即错误了,那么这个物体实际上就是正类;
FP为例,意思是预测为P,即正类,结果为F,即错误了,那么这个物体实际上就是负类。
准确率(Accuracy): ACC=(TP+TN)/(TP+TN+FP+FN)
TP+TN:预测为正类和预测为负类结果都对了的数量,相当于就是预测结果中,预测对了的数量。
精确率(Precision): P=TP/(TP+FP)(分类后的结果中正类的占比)
TP+FP:预测为正的数量。精确率就是说预测为正的数量当中,实际物体也是正类的比例。
召回率(Recall): R=TP/(TP+FN)(所有正例被分对的比例,也称灵敏度)
TP+FN:实际为正的数量。召回率就是说实际上为正的数量当中,被预测为正的数量比例。
特异度(Specificity):S=TN/(TN+FP)(所有负类被分对的比例)
F1 Score:F1=2PR/(P+R)
其中,P代表Precision,R代表Recall。F1-Score指标综合了Precision与Recall的产出的结果。F1-Score的取值范围从0到1的,1代表模型的输出最好,0代表模型的输出结果最差。
混淆矩阵的实例
当分类问题是二分问题是,混淆矩阵可以用上面的方法计算。当分类的结果多于两种的时候,混淆矩阵同时适用。以下面的混淆矩阵为例,我们的模型目的是为了预测样本是什么动物,这是我们的结果: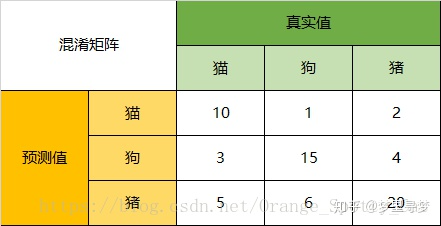
通过混淆矩阵,我们可以得到如下结论:
Accuracy:在总共66个动物中,我们一共预测对了10 + 15 + 20=45个样本,所以准确率(Accuracy)=45/66 = 68.2%。
以猫为例,我们可以将上面的图合并为二分问题: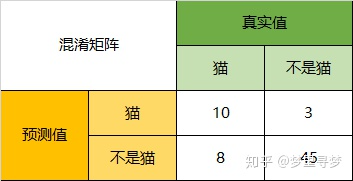
Precision:以猫为例,模型的结果告诉我们,66只动物里有13只是猫,但是其实这13只猫只有10只预测对了。模型认为是猫的13只动物里,有1条狗,两只猪。所以,Precision(猫)= 10/13 = 76.9%
Recall:以猫为例,在总共18只真猫中,我们的模型认为里面只有10只是猫,剩下的3只是狗,5只都是猪。Recall我们前文说过指的就是实际为猫的数量18,我们预测也是猫的数量10的比例,所以,Recall(猫)= 10/18 = 55.6%
Specificity:以猫为例,在总共48只不是猫的动物中,模型认为有45只不是猫。所以,Specificity(猫)= 45/48 = 93.8%。
虽然在45只动物里,模型依然认为错判了6只狗与4只猫,但是从猫的角度而言,模型的判断是没有错的。
F1-Score:通过公式,可以计算出,对猫而言,F1-Score =(2 0.769 0.556)/( 0.769 + 0.556) = 64.54%

