4.1模型选择
4.1.1 误差
- 训练误差:模型在训练数据集上计算得到的误差。用确定的训练数据去做模型训练,模型估计的值与实际确定的训练数据值之间的误差。
- 泛化误差(测试误差):一个新样本在学习的模型上的预计值与它实际上的值之间的差值。
泛化能力:机器学习的目的是学习到一个模型,使它不仅在训练样本上误差小,而且对于未知的新样本的误差小,对新样本的适应能力即可称为泛化能力。
4.1.2 数据集
训练数据集:用来训练模型参数
- 验证数据集:
- 选择模型超参数- 评估模型的好坏- 不能跟训练数据混在一起
- 测试数据集:只用一次的数据集
- k-则交叉验证:在没有足够多的数据时使用
关系:在确定模型之前,不能使用测试数据。
不能仅仅靠训练数据来估计模型,因为无法估计模型的泛化误差。泛化误差与新的样本有关。
4.1.3 过拟合和欠拟合
将模型在训练数据上拟合得比在潜在分布中更接近的现象称为过拟合(overfitting),用于对抗过拟合的技术称为正则化(regularization)
过拟合:数据少模型复杂,把所有的数据都完全拟合,模型的泛化能力很差。
训练误差明显低于验证误差时很可能是这个原因。
欠拟合:数据多模型简单,拟合的效果非常非常差。
训练误差和验证误差都很严重,但它们之间仅有一点差距。<br />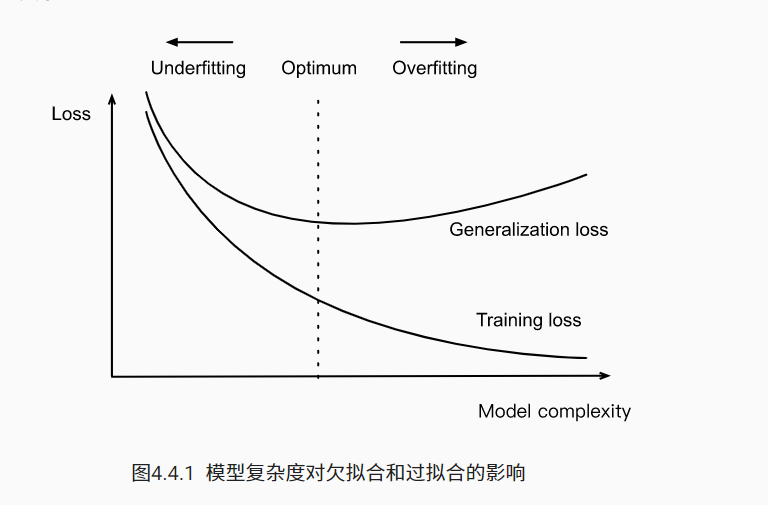
随着模型的一步步训练,训练误差一般逐渐减少,泛化误差逐渐增大,大概会保持到一个相持的状态。
-
4.1.4 模型容量
拟合各种函数的能力
- 低容量的模型难以拟合训练数据
- 高容量的模型可以记住所有的训练数据
4.1.5 影响模型泛化的因素
- 可调整参数的数量。当可调整参数的数量(有时称为自由度)很大时,模型往往更容易过拟合。
- 参数采用的值。当权重的取值范围较大时,模型可能更容易过拟合。
- 训练样本的数量。即使你的模型很简单,也很容易过拟合只包含一两个样本的数据集。而过拟合一个有数百万个样本的数据集则需要一个极其灵活的模型
4.2 正则化技术—权重衰减(L2正则化)
解决overfitting的一种技术。
对w而言,
L2L2正则化回归的小批量随机梯度下降更新如下式: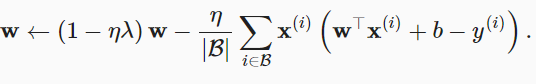
Q:通过加入它,可以解决什么问题????
4.2.2 实现
由于权重衰减在神经网络优化中很常用,深度学习框架为了便于使用权重衰减,便将权重衰减集成到优化算法中,以便与任何损失函数结合使用。此外,这种集成还有计算上的好处,允许在不增加任何额外的计算开销的情况下向算法中添加权重衰减。由于更新的权重衰减部分仅依赖于每个参数的当前值,因此优化器必须至少接触每个参数一次
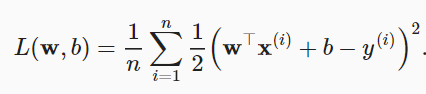
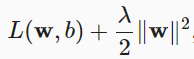 ,λ是正则化参数。较小的λ值对应较少约束的w,而较大的λ值对w的约束更大。
,λ是正则化参数。较小的λ值对应较少约束的w,而较大的λ值对w的约束更大。
