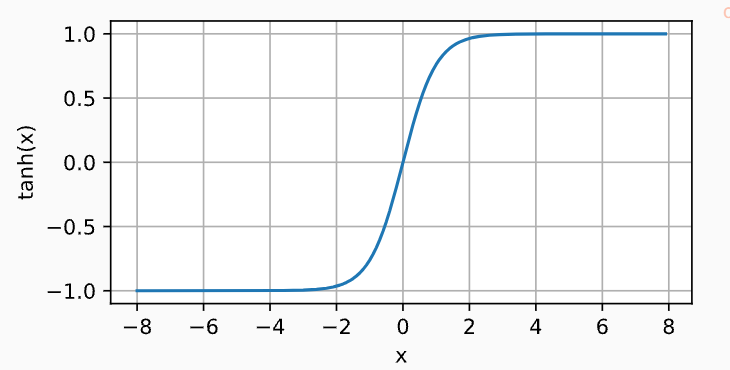
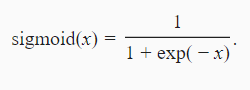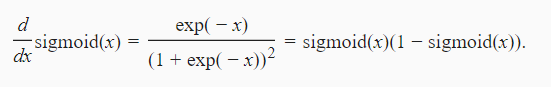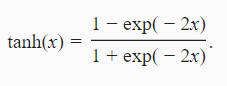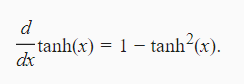4.1 结构

线性模型，故名思义，输出与输入仅仅只存在线性关系。但是对于更复杂的关系，用它处理会有很多限制，所以在输入和输出层之间引入了隐藏层，这种结构就是多层感知机的结构。
而每一个隐藏单元与所有的输入单元和输出单元都有连接，所以也叫全连接。
层数：输入层不涉及运算，所以只算隐藏层和输出层，即为两层。这就是“多层”感知机的由来

4.2 激活函数

4.2.1 ReLU(Rectified linear unit，ReLU）

公式：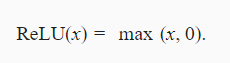
导数：小于0为0，大于0为1，导数要么为0，要么为1，不可能存在梯度爆炸或者梯度消失的情况。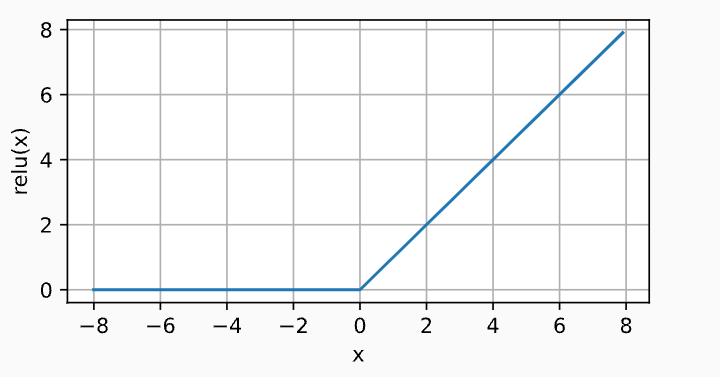

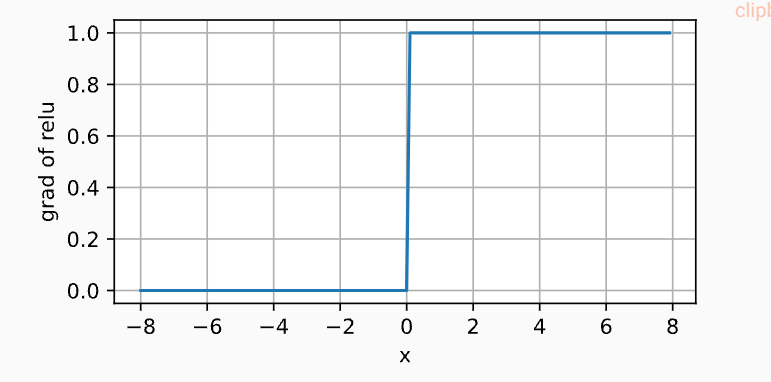
当然，ReLU也有很多变体。

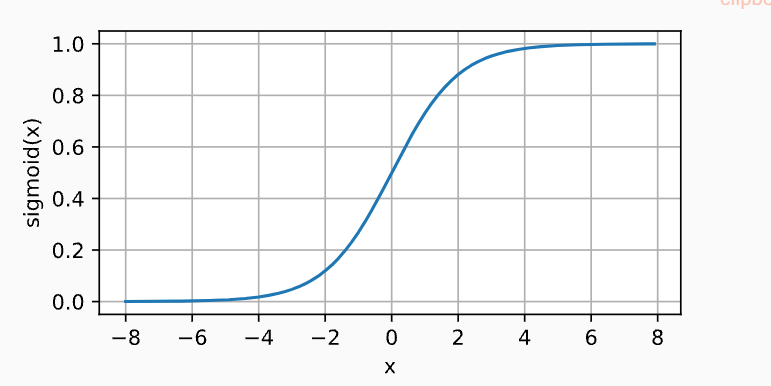
4.2.2 Sigmoid

公式：
导数公式：

导数

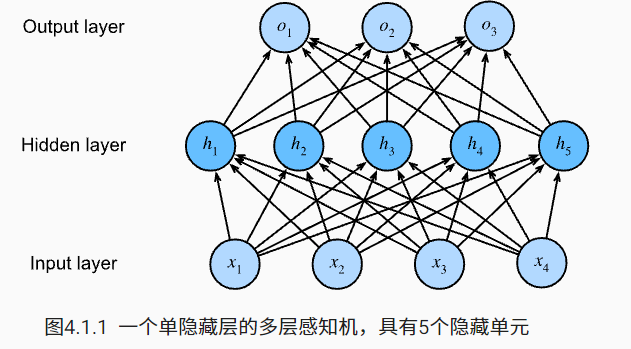
4.2.3 tanh

公式：
导数：

导数

4.3 线性到非线性的实现

以单分类为例
输入层：X∈Rn×d n表示样本数目，d表示输入特征，一个特征对应着一个神经元
隐藏层：权重W(1)∈Rd×h 偏置b(1)∈R1×h h表示隐藏层的神经元个数
输出层：W(2)∈Rh×q b(2)∈R1×q h表示输出层的神经元个数
一个连接对应着一个权重w，一个神经元对应着一个偏置。

如果不应用激活函数，则有
隐藏层的输出：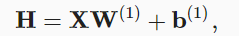
输出层的输出：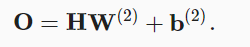

把H的表达式子代入到输出层，则有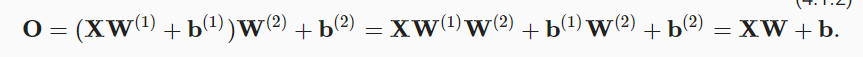

可见，它仍然是一个线性模型。
引入激活函数后，则有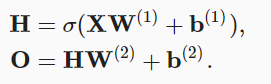

补：权重和偏差的维数

参考：https://www.jiqizhixin.com/articles/2017-11-04-3

4.4 实现

前提：Fashion-MNIST中的每个图像由28×28=78428×28=784个灰度像素值组成。所有图像共分为10个类别

#%%
import torch
from torch import nn
from d2l import torch as d2l
#批量个数
batch_size=256
#训练数据
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size)
#%%
#输入输出，隐藏层的数值
num_inputs,num_outputs,num_hiddens=784,10,256
#参数
#单个隐藏层的多层感知机，当每层神经元与上下神经元都全部相连时，就称为全连接
#注意这些参数的维度
W1=torch.randn(num_inputs,num_hiddens,requires_grad=True)+0.01
b1=torch.zeros(num_hiddens,requires_grad=True)
W2 = torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01
b2 = torch.zeros(num_outputs, requires_grad=True)
params=[W1,b1,W2,b2]
#%%
#激活函数
#为了不让它变成线性的，这样设置隐藏层就没有意义
def relu(X):
    #zeros_like:a与X的大小维度都相同，但是数值为0
    a=torch.zeros_like(X)
    return torch.max(X,a)
#%%
#模型
def net(X):
    X=X.reshape((-1,num_inputs))
    #@表示矩阵乘法
    H=relu(X@W1+b1)
    return (H@W2+b2)
#%%
#损失函数
loss=nn.CrossEntroyLoss()
#%%
#训练
#迭代周期,学习率：10，0.1
num_epochs,lr=10,0.1
#参数的更新，梯度下降
updater=torch.optim.SGDZ(params,lr=lr)
d2l.train_ch3(net,train_iter,test_iter,loss,num_eppchs,updater)
#%%
d2l.predict_ch3(net, test_iter)
#%%

动手学深度学习

4 多层感知机