1、圈复杂度的概念

圈复杂度（Cyclomatic complexity，CC）也称为条件复杂度，是一种衡量代码复杂度的标准，其符号为V(G)。
麦凯布最早提出一种称为“基础路径测试”（Basis Path Testing）的软件测试方式，测试程序中的每一线性独立路径，所需的测试用例个数即为程序的圈复杂度。
圈复杂度可以用来衡量一个模块判定结构的复杂程度，其数量上表现为独立路径的条数，也可理解为覆盖所有的可能情况最少使用的测试用例个数。
圈复杂度可应用在程序的子程序、模块、方法或类别。

1.1、圈复杂度与出错风险

程序的可能错误和高的圈复杂度有着很大关系，圈复杂度最高的模块和方法，其缺陷个数也可能最多。
圈复杂度大说明程序代码的判断逻辑复杂，可能质量低，且难于测试和维护。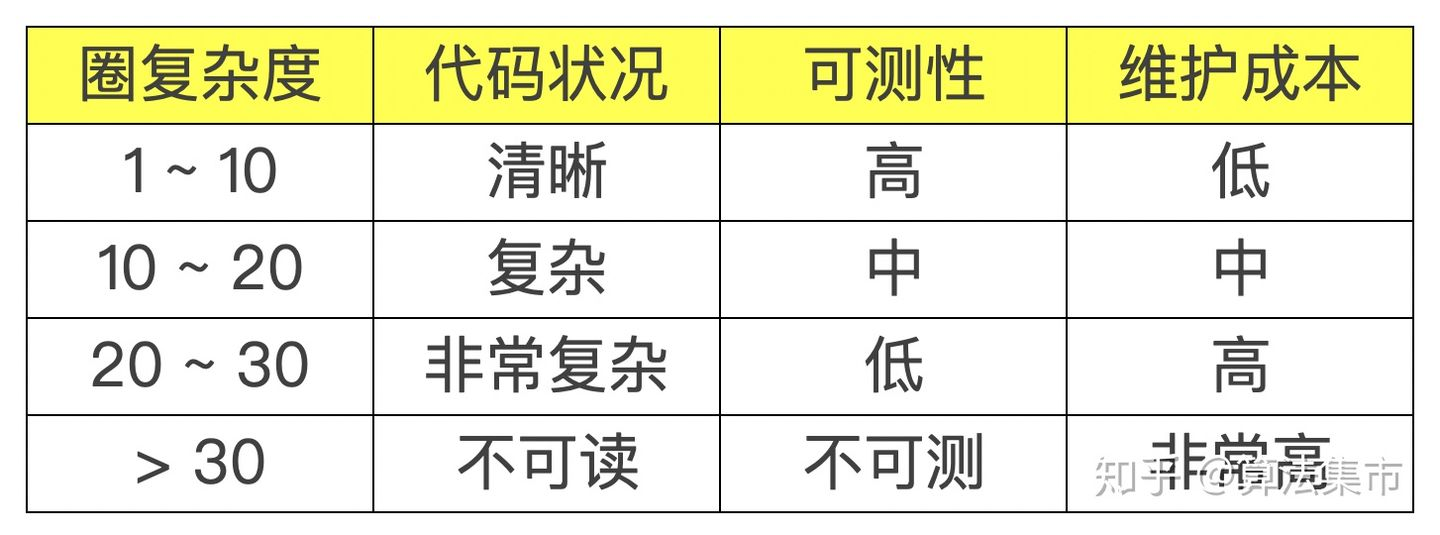
image.png
一般来说，圈复杂度大于10的方法存在很大的出错风险。

1.2、圈复杂度与测试

测试驱动的开发 与 较低圈复杂度值 之间存在着紧密联系。
因为在编写测试用例时，开发人员会首先考虑代码的可测试性，从而倾向编写简单的代码（因为复杂的代码难以测试）。
一个好的测试用例设计经验是：创建数量与被测代码圈复杂度值相等的测试用例，以此提升测试用例对代码的分支覆盖率。

2、圈复杂度的计算方法

圈复杂度有两种计算方法：点边计算法和节点判定法。

2.1、点边计算法

圈复杂度由程序的控制流图来计算：有向图的节点对应程序中个别的代码，而若一个程序运行后会立刻运行另一代码，则会有边连接另一代码对应的节点。
image.png
如上图所示，E表示控制流图中边的数量，N表示控制流图中节点的数量。
圈复杂度的计算公式为：V(G) = E - N + 2

举例说明

下面是正常顺序、if else 和 while 的控制流程图。
image.png

  • 正常顺序的圈复杂度为1；
  • if else 的圈复杂度为2；

  • while 的圈复杂度也为2。

    2.2、节点判定法

    圈复杂度的计算还有另外一种更直观的方法，因为圈复杂度所反映的是“判定条件”的数量，所以圈复杂度实际上就是等于判定节点的数量再加上1。
    对应的计算公式为：V (G) = P + 1
    其中 P 为判定节点数，常见的判定节点有：

  • if 语句

  • while 语句
  • for 语句
  • case 语句
  • catch 语句
  • and 和 or 布尔操作
  • ? : 三元运算符

对于多分支的 case 结构或 if - else if - else 结构，统计判定节点的个数时需要特别注意：必须统计全部实际的判定节点数，也即每个 else if 语句，以及每个 case 语句，都应该算为一个判定节点。

3、计算练习

3.1、练习一

下面代码的圈复杂度为：
1(while) + 1(while) + 1(if) + 1 = 4

  1. void sort(int *A)
  2. {
  3.   int i = 0;
  4.   int n = 5;
  5.   int j = 0;
  6.   while (i < (n - 1)) 
  7.   {
  8.     j = i + 1;
  9.     while (j < n) 
  10.     {
  11.       if (A[i] < A[j]) 
  12.       {
  13.         swap(A[i], A[j]);
  14.       }
  15.     }
  16.     i = i + 1;
  17.   }
  18. }

3.2、练习二

下面代码的圈复杂度为：
1(for) + 2(if) + 1 = 4

  1. int find (int match)
  2. {
  3.   for (int var in list) 
  4.   {
  5.     if (var == match && var != NAN) 
  6.     {
  7.       return var;
  8.     }
  9.   }
  10. }

4、降低圈复杂度的方法

常用的方法有：

  • 简化、合并条件表达式
  • 将条件判定提炼出独立函数
  • 将大函数拆成小函数
  • 以明确函数取代参数
  • 替换算法

原文
https://zhuanlan.zhihu.com/p/139386961