• Understanding the concept of a data stream
• Understanding the characteristics of streaming algorithms
• Sampling representatively and finding majority elements in a stream
  • Algorithms and correctness

What is a data stream?

• A real-time, continuously growing, data sequence.
• Elements of the stream arrive one at a time.
• It is impossible to control the order in which data elements arrive.
• It is unfeasible to locally store a stream in its entirety.

Example: Twitter data

• Tweets arrive in real time
• Can’t control the order in which they arrive
• Can’t store all tweets: around 500 million tweets are generated daily (Source)

More examples

• Social media feeds
• Stock price monitoring
• Sensor data
• Bank transactions
• Road traffic monitoring

Data Streaming Model

Stream: sequence of 𝑚m elements (𝑥1,𝑥2,…,𝑥𝑚) growing over time

• stream at time-step 1: (𝑥1)
• stream at time-step 2: (𝑥1,𝑥2)
• etc.
• We don’t know 𝑚 in advance, and conceptually think of the sequence length as unbounded.

Goal: Compute some function of stream, e.g., median, number of distinct elements, smallest element.
Catch:

1. Limited memory:
   • Cannot store all elements we see
   • Need a data structure that uses limited space (much smaller than 𝑚)
2. Access data sequentially: get one item at a time
3. Process each element quickly: fast updates on the data structure

Finding the minimum: Batch vs Data stream

• Imagine our data is a list of integers.
• We want to find out the minimum of this list.
• In a setting with batch data, you solve it like this:

• But this assumes that data is in memory already.
• How can we approach this if data is a stream?

Minimum over a data stream

1. Read first element and declare it the minimum.
2. Read the second element.
   If it is smaller than the current minimum (first element):
   declare it the minimum.
   Else:
   do nothing.
3. Read the third element.
   If it is smaller than the current minimum:
   declare it the minimum.
   Else: do nothing.

And so on.

Does it count as a streaming algorithm?

• Limited memory? Yes. Only store one element (current minimum) at any single time
• Access data sequentially? Yes.
• Process each element quickly? Yes, only two numbers checked at any point in time
• Will it work if we stop the stream at any given point? Yes, the element declared minimum will have been the smallest element we’ve seen

from math import inf
class StreamingMinimum:
    def __init__(self):
        self.result = inf  # Immediately replaced by the 1st element
    def update(self, element):
        self.result = min(self.result, element)
import numpy as np
stream = np.random.randint(low=0, high=20, size=10)  # Simulate a stream
print("Data:", stream)
s = StreamingMinimum()
for element in stream: # read next element of stream
    s.update(element) # update minimum element
print(s.result)

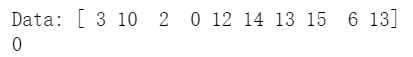
The algorithm works because the minimum can be computed incrementally over the stream: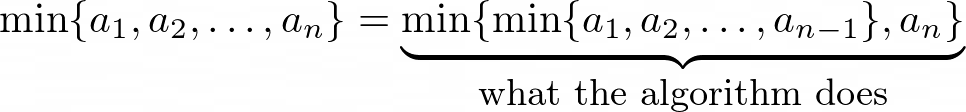

Sampling a stream

• Stream sampling is the process of collecting a representative sample of the elements of a data stream.
• Sample is usually much smaller than the entire stream, but can be designed to retain important characteristics of the stream, and can be used to estimate many important aggregates on the stream.
• Crucial for many streaming applications

Sampling batch data

• Imagine that you have a dataset and you want to uniformly sample an object
• How to do this?
• If you know the size 𝑛 of the data set, you can uniformly draw a random number 𝑘 between 11 and 𝑛, scan the data set and take the 𝑘-th element. ```python from random import randrange

data = np.random.randint(low=0, high=20, size=10) print(“Data:”, data) k = randrange(10) print(“k:”, k) sample = data[k] print(“Sample”, sample)

![image.png](https://cdn.nlark.com/yuque/0/2021/png/471483/1639767004988-99903045-aee5-47d4-bd9f-0919bf86246a.png#clientId=u8ea9dfe2-9ff9-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=102&id=u9bd6f1ac&margin=%5Bobject%20Object%5D&name=image.png&originHeight=95&originWidth=423&originalType=binary&ratio=1&rotation=0&showTitle=false&size=6232&status=done&style=none&taskId=u91d0cb38-dac2-45c9-9e4a-af9b49867e7&title=&width=454.5)
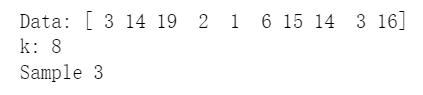<a name="FHz7v"></a>
## Sampling a data stream
- But now imagine that you have a data stream
- How do you take a sample from a stream of unknown length?
- You don't know which range to draw your random index from.
- This problem has a nice solution, called **Reservoir Sampling**.
<a name="hbwa2"></a>
## Reservoir Sampling(蓄水池抽样)
- **Problem**: Uniformly sample an element 𝑠 from a stream (𝑎1,𝑎2,...) of unknown length. The 𝑖'th element should be selected as 𝑠 with probability 1/𝑛 at some time 𝑛≥𝑖. 蓄水池抽样算法可以在未知长度的序列中随机抽样
- **Algorithm**:
   - 1. Read first element 𝑎1 and set s=𝑎1. 
   - 2. On seeing the i'th element 𝑎1:     
      - with probability 1/i, set s=𝑎1 (i.e., replace previously selected element)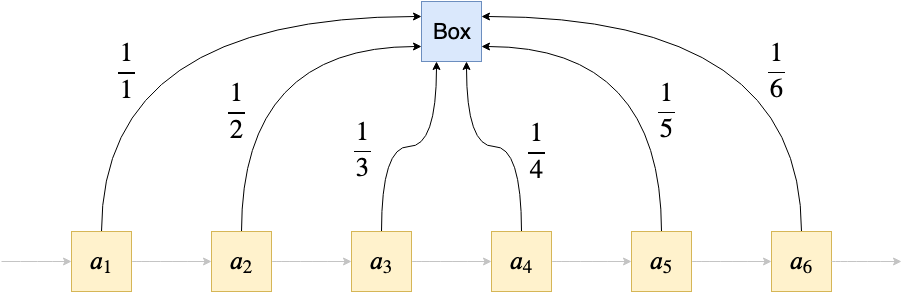
![image.png](https://cdn.nlark.com/yuque/0/2021/png/471483/1639767099017-ad3b738f-ba40-49d3-acf7-982e1f485486.png#clientId=u8ea9dfe2-9ff9-4&crop=0&crop=0&crop=1&crop=1&from=paste&id=u6220eb28&margin=%5Bobject%20Object%5D&name=image.png&originHeight=292&originWidth=902&originalType=url&ratio=1&rotation=0&showTitle=false&size=25920&status=done&style=none&taskId=ucccaaf15-6adf-4251-baad-e30ff037049&title=)<br />![image.png](https://cdn.nlark.com/yuque/0/2021/png/471483/1639922569407-00536288-2895-4273-9376-d37b80baff34.png#clientId=u6e0e5ec3-0281-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=324&id=u010d481a&margin=%5Bobject%20Object%5D&name=image.png&originHeight=484&originWidth=873&originalType=binary&ratio=1&rotation=0&showTitle=false&size=74698&status=done&style=none&taskId=u4fdc6957-9658-4740-82a5-bcefc44bac4&title=&width=584.5)<br />时间复杂度：按行读取，O（n）;<br />空间复杂度：内存中只保存了s一行，O（1）<br />**从不知长度的n行里选k行**
```python
from random import random
class ReservoirSampler:
    def __init__(self):
        self.sample = None # sampled element
        self.n = 0 # number of elements from stream traversed so far (i.e. t)
    def update(self, element):
        self.n += 1     # we see a new stream element
        if random() < 1 / self.n:  # satisfied with prob. 1/n.
            self.sample = element # update sample to new stream element
stream = np.arange(20) # A simulated stream
r = ReservoirSampler()
for e in stream: # receive stream elements one at a time
    r.update(e)
print("Sampled element:", r.sample)

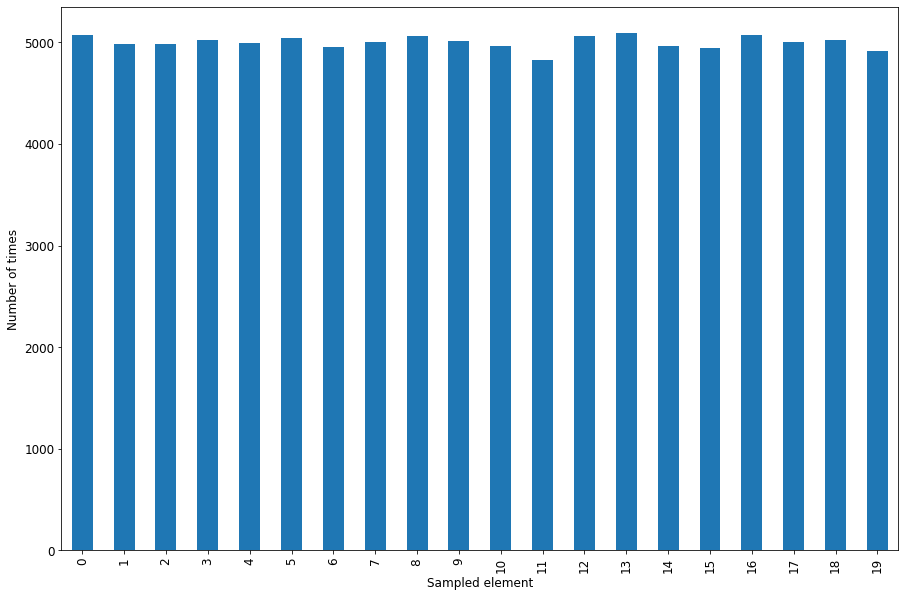
• Let’s run an experiment
• 100.000 times, we’ll sample the stream np.arange(20) using the method above.
• We’ll record the number sampled each time after traversing the entire stream.
• And the result is…

• when : selected with probability . Good.
• when :
  • selected with probability
  • selected with probability . Good.
• when :
  • selected with probability
  • selected with probability . Good.
  • selected with probabilit . Good.
• What’s the probability that at some time ?

From algorithm we have:

%20%3D%20%5Cfrac%7B1%7D%7Bi%7D#card=math&code=P%28a_i%20%5Ctext%7B%20selected%20at%20%7D%20i%29%20%3D%20%5Cfrac%7B1%7D%7Bi%7D&id=JFBP4), hence %20%3D%201%20-%20%5Cfrac%7B1%7D%7Bi%7D%20%3D%20%5Cfrac%7Bi-1%7D%7Bi%7D#card=math&code=P%28a_i%20%5Ctext%7B%20not%20selected%20at%20%7D%20i%29%20%3D%201%20-%20%5Cfrac%7B1%7D%7Bi%7D%20%3D%20%5Cfrac%7Bi-1%7D%7Bi%7D&id=QKY0z).

Therefore



for all seen at time : The property we were after.

从不知长度的n行里选k行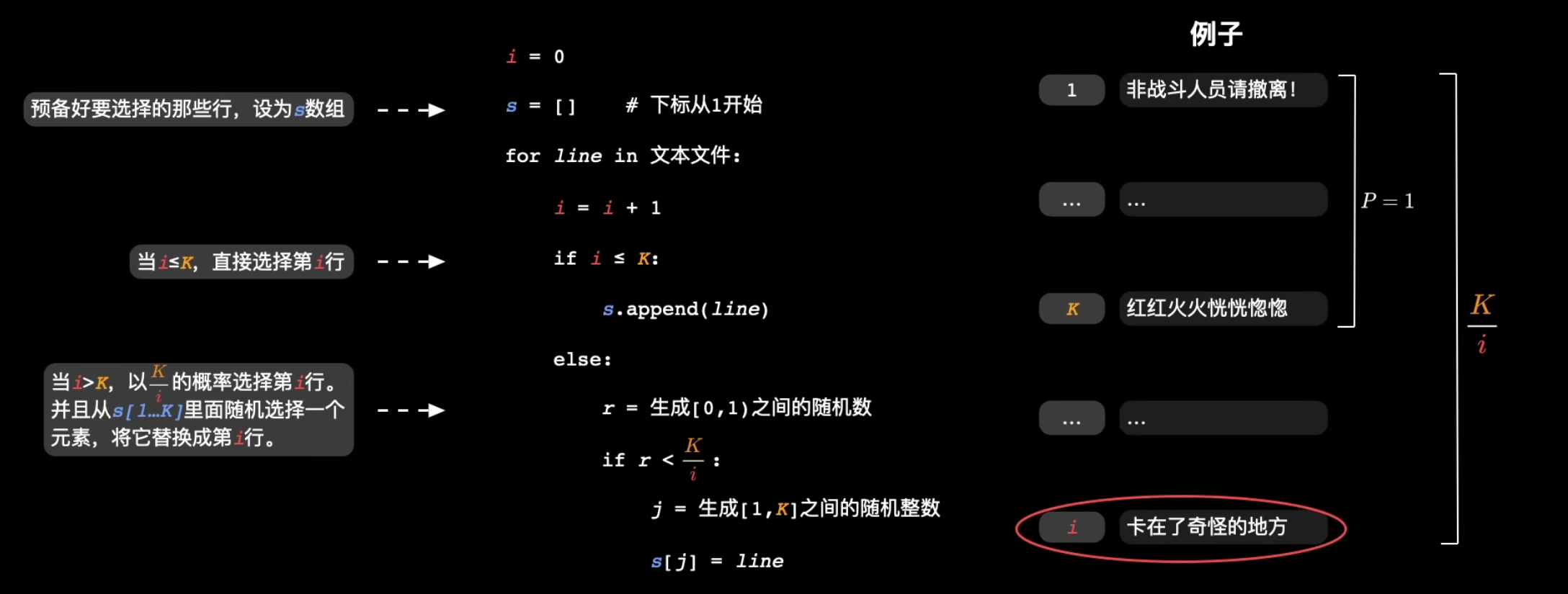




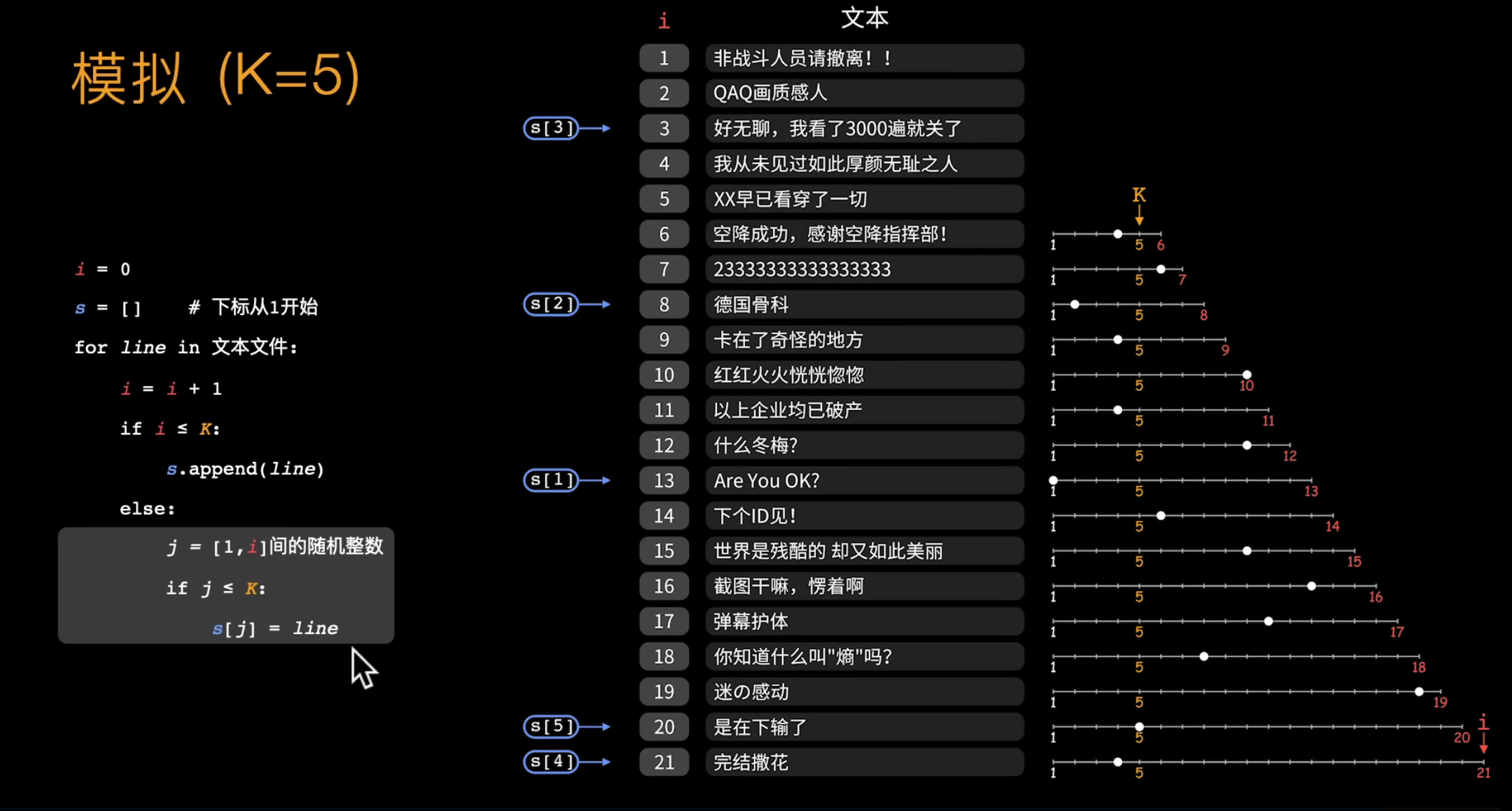
Suppose number of lines on input file is N.
Time complexity: O(N).
Space complexity: O(K) (regardless of the size of per line in file).

Does it count as a streaming algorithm?

• Limited memory? Yes. Only store two things (current sample, number of stream elements seen) at any single time.
• Access data sequentially? Yes.
• Process each element quickly? Yes, only requires a biased coin toss at each time-step.
• Will it work if we stop the stream at any given point? Yes, at time 𝑛n each element seen has equal probability of being selected as 𝑠s.

Reservoir sampling with a reservoir of size 𝑘k

• The method described above samples 1 element from the stream. That is, it has a reservoir of size 1.
• In its general form, reservoir sampling generates a sample of 𝑘 elements from the stream.
  • This algorithm (implemented by you in Project 3) has the property that at time 𝑛≥𝑘, 𝑃(𝑒∈𝑠𝑎𝑚𝑝𝑙𝑒𝑟)=𝑘/𝑛 for all 𝑒 in (𝑎1,𝑎2,…,𝑎𝑛): Each element in the stream input has equal probability of being in the generated sample.

Computing frequent elements

A very useful statistic for many streaming applications is to keep track of elements that occur frequently.

• This type of problem come in several flavours.
• Mode : Find the element (or elements) with the highest frequency.
• Majority: Find the element with strictly more than 50% occurrence in the stream - note that there may not be a majority elements in a stream.
• Threshold: Find all elements that occur more than 𝑓 fraction of the stream for any 0<𝑓≤1. Finding majority is a special case with 𝑓>1/2.

Examples

• Which IP is accessing the website most often?
• Who is posting the majority of the tweets?

Boyer–Moore majority vote algorithm(多数投票法)

https://www-igm.univ-mlv.fr/~lecroq/string/node14.html#SECTION00140
https://en.m.wikipedia.org/wiki/Boyer%E2%80%93Moore_majority_vote_algorithm

• An algorithm for finding the majority element in a stream, if it exists.

Initialize a majority candidate m with m = None
Initialize a counter c with c = 0
For each element x of the input stream:
If c = 0:
assign m = x and c = 1
else if m = x (x is already the majority element):
then assign c = c + 1
else (x is not the majority element and c != 0):
assign c = c − 1
Return m

Stream (8 elements): AABBBAAA

• Majority element: A (5 votes)

Initialisation

Does it count as a streaming algorithm?¶

• Limited memory? Yes. Only store two things (current majority candidate, and counter) at any single time.
• Access data sequentially? Yes.
• Process each element quickly? Yes, few equality comparisons and increment/decrement operations.
• Will it work if we stop the stream at any given point? Yes (see Correctness below)

Properties of Boyer-Moore

• If the Boyer–Moore majority vote algorithm returns majority_element 𝑒e, it either holds that 𝑒e is the majority element or there isn’t a majority element.
• Can give false positives: no majority element exists, but m is not None.
• The algorithm can be modified to avoid false positives.

Correctness of Boyer-Moore

Invariant: After ‘th element the values and are such that we can divide the elements seen into two groups:

• : Of size all in favor of
• : Of size that can be paired to disagree on element value

Proposition: Assuming Invariant, has majority if there is a majority.

Proof of Proposition: By contradiction. Suppose some has majority i.e. more than votes. Then at most votes for come from group . Therefore must have a vote from group , contradicting that all votes in are for . (If then is empty and so there’s still not enough votes for to have majority).

Proof of Invariant: By induction on .

Base case: If then we can form #card=math&code=U%20%3D%20%28a_1%29&id=ClW8B) and is empty and and .

Induction step: Suppose the invariant holds at (for , , and ) and we are to consider the #card=math&code=%28i%2B1%29&id=zT2Du)’st element (how to form , , and ).

If then is empty, so #card=math&code=U%27%20%3D%20%28a%7Bi%2B1%7D%29&id=XUIS6) and and and : We can form as a single element group and keep as before.

If and , then is plus and and and : We can add the new element to and keep as before.

If and , then there’s in such that and so is different from (they disagree). Therefore is minus and is plus #card=math&code=%28a_%7Bi%2B1%7D%2C%20a_j%29&id=FGt9h) and and : We can add a disagreeing pair to using some element in (which is then removed).