对于二分类问题,机器预测的和实际的还是会有所偏差,所以我们引入以下几个概念来评价分类器的优良。
一、TP、TN、FP、FN 概念
首先有关 TP、TN、FP、FN 的概念。大体来看,TP 与 TN 都是分对了情况,TP 是正类,TN 是负类。则推断出,FP 是把错的分成了对的,而 FN 则是把对的分成了错的。(我的记忆方法:首先看第一个字母是 T 则代表分类正确,反之分类错误;然后看 P,在 T 中则是正类,若在 F 中则实际为负类分成了正的。)
【举例】一个班里有男女生,我们来进行分类,把女生看成正类,男生看成是负类。我们可以用混淆矩阵来描述 TP、TN、FP、FN。
混淆矩阵
| | 相关(Relevant),正类 | 无关(NonRelevant),负类 |
| 被检索到(Retrieved) | True Positives(TP,正类判定为正类。即女生是女生) | False Positives(FP,负类判定为正类,即 “存伪”。男生判定为女生) |
| 未被检索到(Not Retrieved) | False Negatives(FN,正类判定为负类,即 “去真”。女生判定为男生) | True Negatives(TN,负类判定为负类。即男生判定为男生) |
二、准确率、精确率(精准率)、召回率、F1 值
1. 准确率(Accuracy)。顾名思义,就是所有的预测正确(正类负类)的占总的比重。
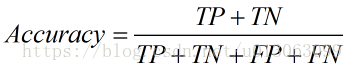
2. 精确率(Precision),查准率。即正确预测为正的占全部预测为正的比例。个人理解:真正正确的占所有预测为正的比例。
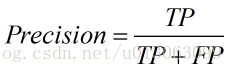
3. 召回率(Recall),查全率。即正确预测为正的占全部实际为正的比例。个人理解:真正正确的占所有实际为正的比例。
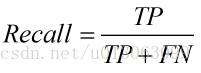
4.F1 值(H-mean 值)。F1 值为算数平均数除以几何平均数,且越大越好,将 Precision 和 Recall 的上述公式带入会发现,当 F1 值小时,True Positive 相对增加,而 false 相对减少,即 Precision 和 Recall 都相对增加,即 F1 对 Precision 和 Recall 都进行了加权。
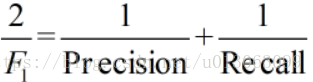
公式转化之后为:
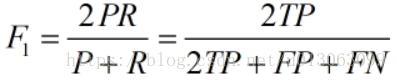
三、ROC 曲线、AUC 值
1.ROC 曲线。接收者操作特征曲线(receiver operating characteristic curve),是反映敏感性和特异性连续变量的综合指标,ROC 曲线上每个点反映着对同一信号刺激的感受性。下图是 ROC 曲线例子。
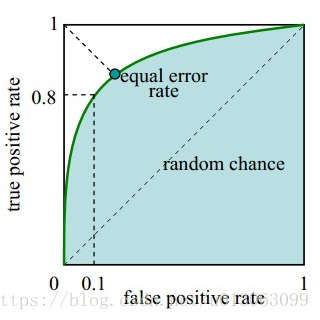
横坐标:1-Specificity,伪正类率 (False positive rate,FPR,FPR=FP/(FP+TN)),预测为正但实际为负的样本占所有负例样本的比例;
纵坐标:Sensitivity,真正类率 (True positive rate,TPR,TPR=TP/(TP+FN)),预测为正且实际为正的样本占所有正例样本的比例。
在一个二分类模型中,假设采用逻辑回归分类器,其给出针对每个实例为正类的概率,那么通过设定一个阈值如 0.6,概率大于等于 0.6 的为正类,小于 0.6 的为负类。对应的就可以算出一组 (FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小,越来越多的实例被划分为正类,但是这些正类中同样也掺杂着真正的负实例,即 TPR 和 FPR 会同时增大。阈值最大时,对应坐标点为 (0,0),阈值最小时,对应坐标点 (1,1)。
真正的理想情况,TPR 应接近 1,FPR 接近 0,即图中的(0,1)点。ROC 曲线越靠拢(0,1)点,越偏离 45 度对角线越好 **。**
2.AUC 值。AUC (Area Under Curve) 被定义为 ROC 曲线下的面积,显然这个面积的数值不会大于 1。又由于 ROC 曲线一般都处于 y=x 这条直线的上方,所以 AUC 的取值范围一般在 0.5 和 1 之间。使用 AUC 值作为评价标准是因为很多时候 ROC 曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应 AUC 更大的分类器效果更好。
从 AUC 判断分类器(预测模型)优劣的标准:
- AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
一句话来说,AUC 值越大的分类器,正确率越高。
灵敏度=真阳性人数/(真阳性人数+假阴性人数)100%。正确判断病人的率;
特异度=真阴性人数/(真阴性人数+假阳性人数))100%。正确判断非病人的率;其中真阳性、假阴性、真阴性和假阳性均为检测值,
【参考文献】
https://www.jianshu.com/p/c61ae11cc5f6
https://www.cnblogs.com/sddai/p/5696870.html
https://blog.csdn.net/xyzx043874/article/details/54969239
https://blog.csdn.net/weeeeeida/article/details/78906570
https://blog.csdn.net/u013063099/article/details/80964865
https://blog.csdn.net/u013063099/article/details/80964865

