决策树

1.熵

（1）信息熵

信息论中，熵度量了事物的不确定性，越不确定的事物，它的熵就越大。它的定义如下：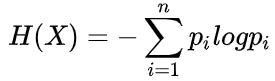

（2）条件熵

条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性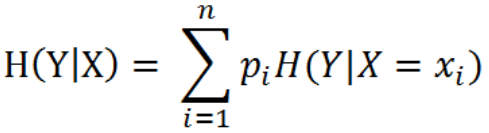

（3）信息增益

特征A对训练数据集D的信息增益g(D, A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即：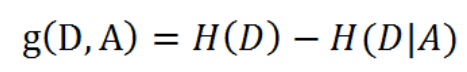

2.ID3算法

（1）算法过程

SNS社区中不真实账号检测的例子说明如何使用ID3算法构造决策树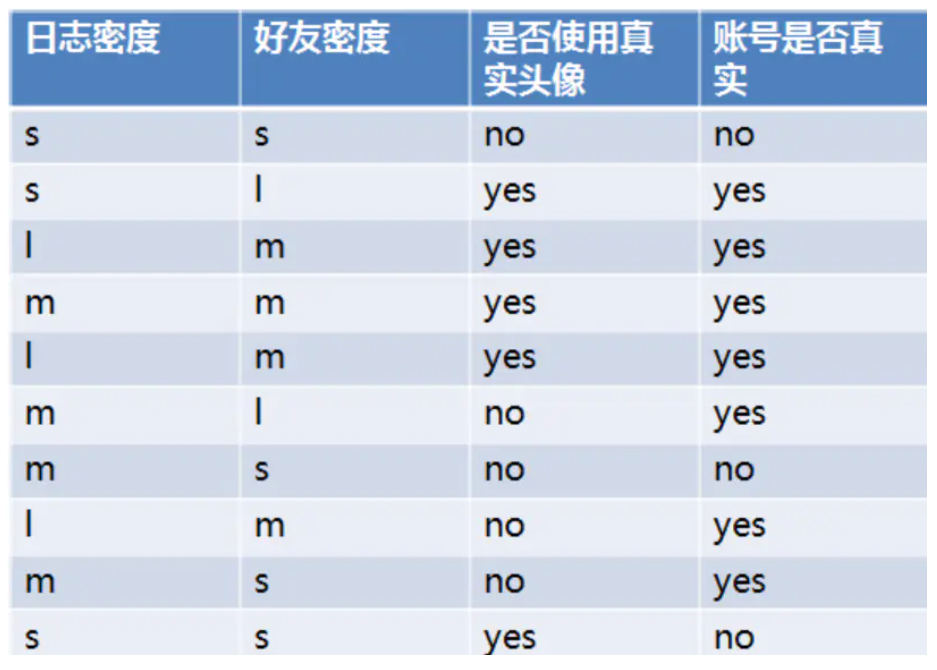

设L、F、H和D表示日志密度、好友密度、是否使用真实头像和账号是否真实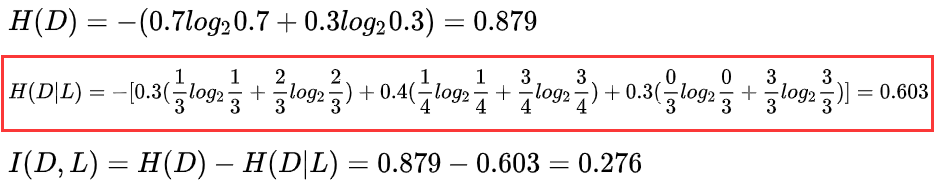

主要关注计算公式中间部分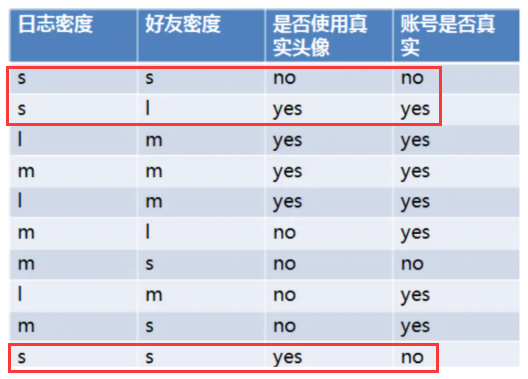

当日志密度是S的时候，账号是真的概率为1/3，假的为2/3；信息增益为-[0.3(1/3log2(1/3)+2/3*log2(2/3))]，用这种方式可以计算日志密度为M和L的信息增益。最终日志密度的信息增益为0.276。
（2）计算好友密度的信息增益为0.033，是否有真实头像的信息增益为0.553。因为是否有真实头像，有最大的增益，因此选择是否有真实头像为第一个节点分裂属性。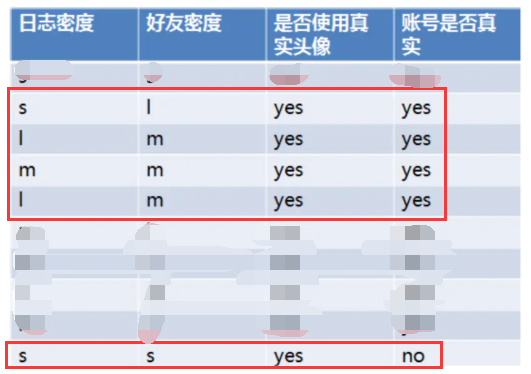

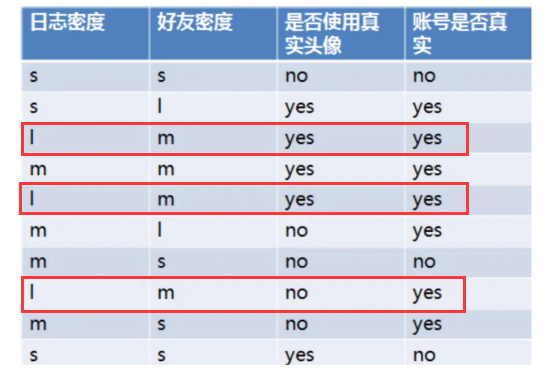
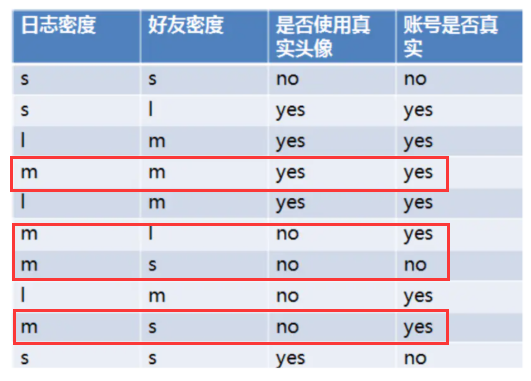
找到所有真实使用头像的，然后来计算日志密度和好友密度分别的信息增益是多少，选择信息增益最大的作为下一个分裂节点属性；同样，找到所有非真实使用头像的，找到这个节点下的最大信息增益。因此，再第一个节点找好后，两个子节点的下一个节点是有可能不一样的。

（2）算法不足

（1）ID3没有考虑连续特征，比如长度，密度都是连续值，无法在ID3运用。这大大限制了ID3的用途。
（2）ID3采用信息增益大的特征优先建立决策树的节点。很快就被人发现，在相同条件下，取值比较多的特征比取值少的特征信息增益大。
（3）ID3算法对于缺失值的情况没有做考虑
（4） 没有考虑过拟合的问题

3.C4.5算法

（1）算法过程

C4.5算法可以有效解决ID3算法信息增益倾向于特征多的特征这一不足，它和ID3的不同之处在于它计算了一个属性分裂信息度量，属性分裂信息度量考虑了属性进行分裂时分支的数量信息和尺寸信息。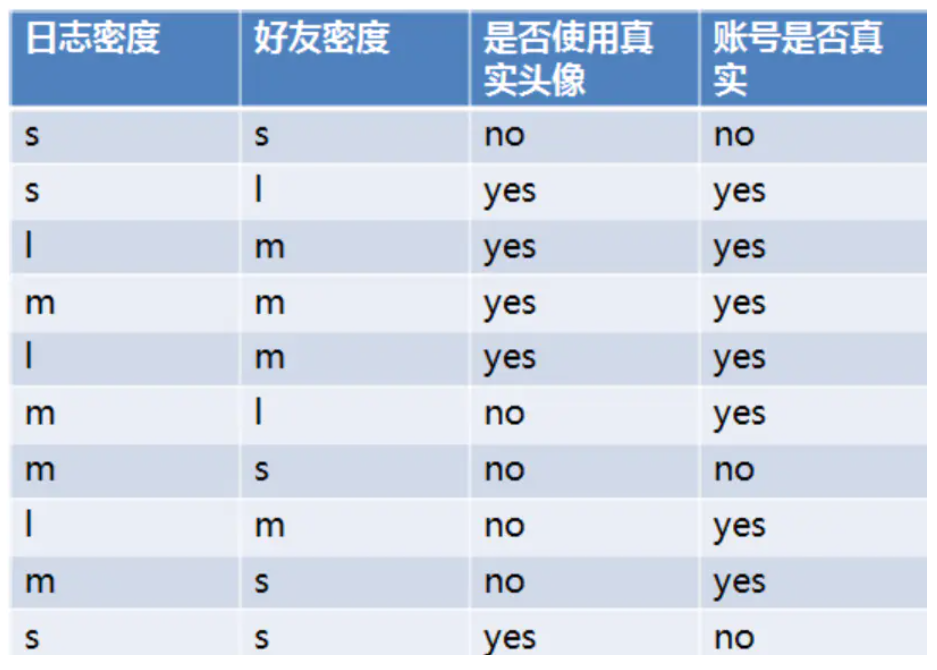

还是以上面的为例
H（日志密度）=(-3/10)log(3/10)+(-3/10)log(3/10)+(-4/10)*log(4/10)=1.57
在计算一个日志密度的信息增益率(Information Gain Rate)：
IGR(日志密度) = Gain(日志密度)/H(日志密度) = 0.276/1.57=0.175

（2）算法不足

（1）剪枝策略可以再优化；
（2）C4.5 用的是多叉树，用二叉树效率更高；
（3）C4.5 只能用于分类；
（4）C4.5 使用的熵模型拥有大量耗时的对数运算，连续值还有排序运算；
（5）C4.5 在构造树的过程中，对数值属性值需要按照其大小进行排序，从中选择一个分割点，所以只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时，程序无法运行。

4.CART算法

（1）算法过程

CART是一棵二叉树，采用二元切分法，每次把数据切成两份，分别进入左子树、右子树。CART采用GINI增益来进行划分。例如上面的例子中，是否使用真实头像，它的GINI增益为：

使用真实头像的总个数为5，账号真实的个数为4，非真实的个数为1
GINI=1-[(1/5)+(4/5)]=8/25
使用非真实头像的个数为5，账号真实的个数为3，非真实的个数为2
GINI=1-[(2/5)+(3/5)]=12/25
可以计算出GINI增益：
GINI_Gain = (8/25)(5/10)+(12/25)(5/10)=2/5
CART树采用GINI增益最小的作为划分的依据。

（2）注意事项

（1）CART的剪枝都是按照二分类来的，如果不能二分类，要把它变为二分类。例如上面的日志密度包含三个类别，在分类的时候，可以分为【S, M】和【L】这两类，也可以分为【S, L】和【M】以及【M, L】和【S】，在计算基尼增益的时候，分别计算三种不同的分类方式的基尼增益，取最小的基尼增益作为划分方式。
（2）对于连续变量的处理：例如周志华的西瓜那个例子，有一个属性是密度，这个属性属于数值型的，并且不是连续的，它可以按照如下的方式进行处理。

（3）无论是ID3,C4.5还是CART，模型一般都会有剪枝，剪枝主要是为了预防过拟合，主要思路是从叶节点向上回溯，尝试对某个节点进行剪枝，比较剪枝前后的决策树的损失函数值。