1.蒙特卡罗方法

（1）简介

蒙特卡罗方法是一种计算方法。原理是通过大量随机样本，去了解一个系统，进而得到所要计算的值。第一个例子是，如何用蒙特卡罗方法计算圆周率π。正方形内部有一个相切的圆，它们的面积之比是π/4。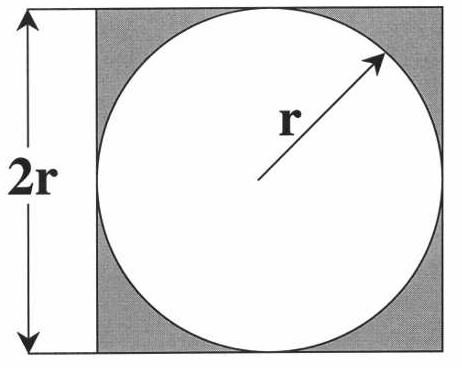
image.png
圆的面积和正方形面积的比值为
image.png
现在，在这个正方形内部，随机产生10000个点（即10000个坐标对 (x, y)），计算它们与中心点的距离，从而判断是否落在圆的内部。如果这些点均匀分布，那么圆内的点应该占到所有点的 π/4，因此将这个比值乘以4，就是π的值。
以上内容选自阮一峰的网络日志

（2）引入

问题：求下面阴影部分面积，用什么方法？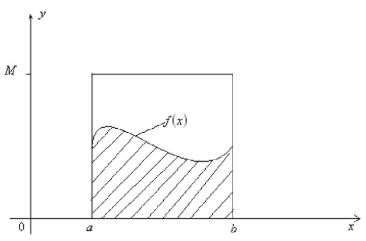
image.png
方法1：采样[a,b]区间的n个值：x,x,…x,用它们的均值来代表[a,b]区间上所有的f(x)的值。这样我们上面的定积分的近似求解为(b−a)f(x)
不足：这种方法隐含了一个假定，即x在[a,b]之间是均匀分布的，而绝大部分情况，x在[a,b]之间不是均匀分布的。如果我们用上面的方法，则模拟求出的结果很可能和真实值相差甚远。
PS：均匀分布的概率密度函数为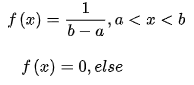
image.png
方法2：如果我们可以得到x在[a,b]的概率分布函数p(x)，那么我们的定积分求和可以这样进行：
image.png
这里：[f(x)/p(x)]p(x)可以看做是 f(x)/p(x)基于概率分布p(x)的期望(样本统计量概率)，那么我们可以用期望的方法来求这个式子的值。而计算期望的一个近似方法是取f(x)/p(x)的若干个基于分布p(x)的采样点，然后求平均值得到。

2.概率分布采样

对于常见的均匀分布uniform(0,1)是非常容易采样样本的，通过线性同余发生器可以很方便的生成(0,1)之间的伪随机数样本。而其他常见的概率分布（比如t分布，F分布，Beta分布，Gamma分布等），无论是离散的分布还是连续的分布，它们的样本都可以通过uniform(0,1)的样本转换而得。在python的numpy，scikit-learn等类库中，都有生成这些常用分布样本的函数可以使用。但是如果我们的x的概率分布不是常见的分布，这意味着我们没法方便的得到这些非常见的概率分布的样本集，就需要用到接受-拒绝采样。

3.接受-拒绝采样

对于概率分布不是常见的分布，一个可行的办法是采用接受-拒绝采样来得到该分布的样本。既然 p(x) 太复杂在程序中没法直接采样，那么我设定一个程序可采样的分布q(x)比如高斯分布，然后按照一定的方法拒绝某些样本，以达到接近p(x)分布的目的。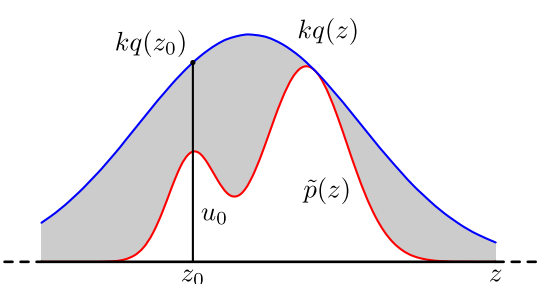
image.png
具体过程如下，设定一个方便采样的常用概率分布函数q(x)，以及一个常量k，使得p(x)总在kq(x)的下方。
【1】采样得到q(x)的一个样本z，如果u落在了上图中的灰色区域，则拒绝这次抽样，否则接受这个样本z。
【2】重复以上过程得到n个接受的样本z,z,….z,则最后的蒙特卡罗方法求解结果为（按照1中的蒙特卡洛方法思想）：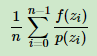
image.png
接受-拒绝采样也只能部分满足我们的需求，在很多时候我们还是很难得到我们的概率分布的样本集。比如：
1）对于一些二维分布p(x,y)，有时候我们只能得到条件分布p(x|y)和p(y|x)和,却很难得到二维分布p(x,y)一般形式，这时我们无法用接受-拒绝采样得到其样本集。
2）对于一些高维的复杂非常见分布p(x1,x2,…,xn)，我们要找到一个合适的q(x)和k非常困难。
要想将蒙特卡罗方法作为一个通用的采样模拟求和的方法，必须解决如何方便得到各种复杂概率分布的对应的采样样本集的问题，而马尔科夫链就是帮助找到这些复杂概率分布的对应的采样样本集的白衣骑士。
以上内容选自刘建平的博客

4.马尔科夫链

马尔科夫链：时间、状态都是离散的马尔可夫过程称为马尔可夫链。
马尔科夫过程：它假设某一时刻状态转移的概率只依赖于它的前一个状态。

（1）例子


先说说我们村智商为0的王二狗，人傻不拉几的，见人就傻笑，每天中午12点的标配，仨状态：吃，玩，睡。这就是传说中的状态分布。
image.png
先看个假设，他每个状态的转移都是有概率的
image.png
这个矩阵就是转移概率矩阵P，并且它是保持不变的，就是说第一天到第二天的转移概率矩阵跟第二天到第三天的转移概率矩阵是一样的。有了这个矩阵，再加上已知的第一天的状态分布，就可以计算出第N天的状态分布了。
image.png
这里计算一下4月2号状态是吃的概率P=0.60.2+0.20.1+0.2*0.4=0.22。总结：马尔可夫链就是这样一个任性的过程，它将来的状态分布只取决于现在，跟过去无关。
以下内容选自知乎

（2）性质