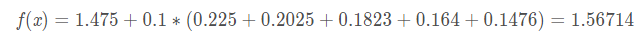1.算法简介

GBDT（Gradient Boosting Decision Tree ，梯度提升决策树），和其他的Gradient Boosting方法一样，每一次计算是为了减少上一次的残差，而为了消除残差，可以在残差减少的梯度(Gradient)方向上建立一个新的模型。GBDT 要求弱学习器必须是CART模型。GBDT模型最后的输出，是一个样本在各个树中输出的结果的和。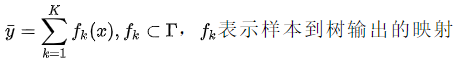
image.png

2.算法示例

下面示例选自CSDN博客

（1）数据准备

如下表所示：一组数据，特征为年龄、体重，身高为标签值。共有5条数据，前四 条为训练样本，最后一条为要预测的样本。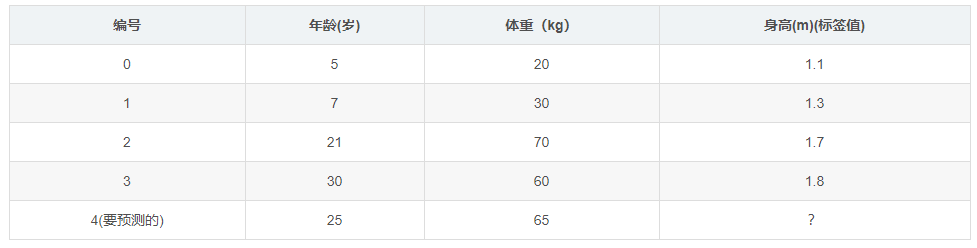
image.png

（2）参数设置

  • 学习率：learning_rate=0.1
  • 迭代次数：n_trees=5
  • 树的深度：max_depth=3

（3）初始化弱学习器

第一个弱学习器表达为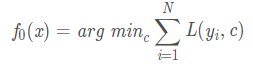
image.png
PS:arg min F(x,y)指当F(x,y)取得最小值时，变量x,y的取值。这里损失函数为平方损失，是一个凸函数，求最小值可以直接求导，令倒数等于零，得到c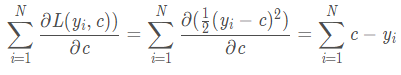
image.png
也即4个样本的均值在，可以得到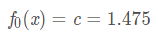
image.png

（4）拟合残差

计算残差，第一轮相当于无论什么样的样本，都无脑的预测它的身高为1.475m。可以计算这个值和真实值之间的残差，再来拟合残差。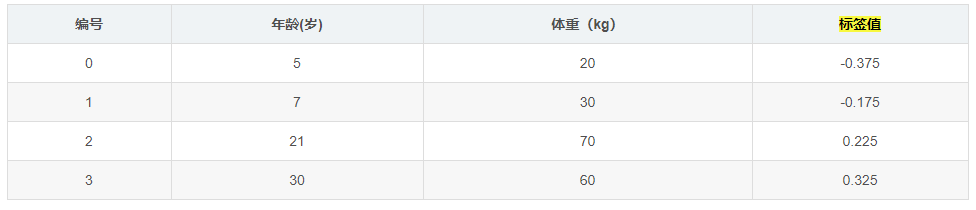
image.png
第二轮寻找回归树的最佳划分节点，遍历每个特征的每个可能取值，分别计算分裂后两组数据的平方损失。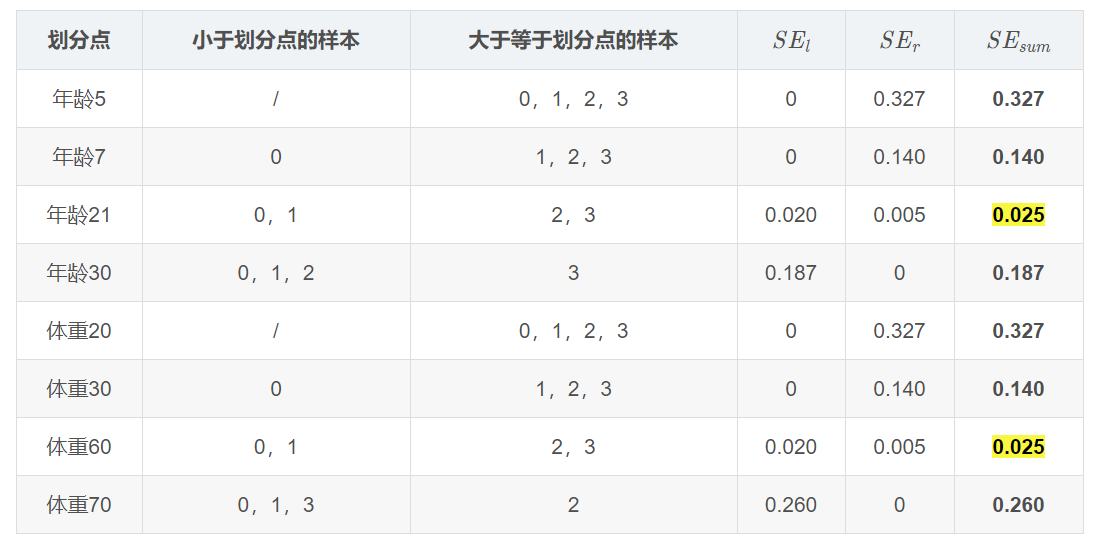
image.png
这个是怎么得到的呢？以年龄为7为例，小于7的只有一个样本，大于7的有编号1,2,3这三个样本，可以计算出一个均值（0.325+0.225-0.175）=0.125，方差为（(-0.175-0.125)+(0.225-0.125)+(0.325-0.125)）=0.14。以上划分点是的总平方损失最小为0.025有两个划分点：年龄21和体重60，所以随机选一个作为划分点，这里我们选年龄21，现在我们的第一棵树长这个样子：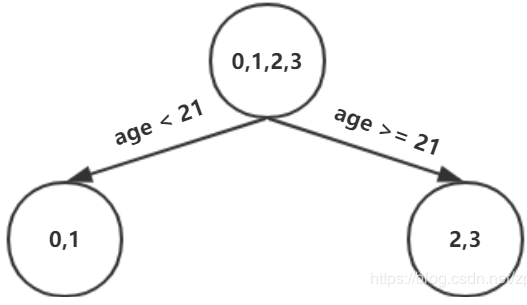
image.png
我们设置的参数中树的深度max_depth=3，现在树的深度只有2，需要再进行一次划分，这次划分要对左右两个节点分别进行划分，对于左节点只有0,1两个样本：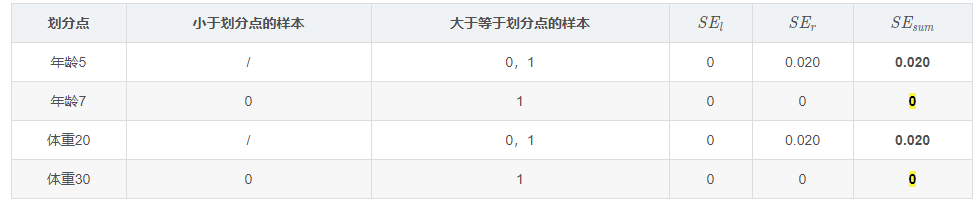
image.png
可以选择年龄7作为划分。对于右节点，只有2,3两个样本：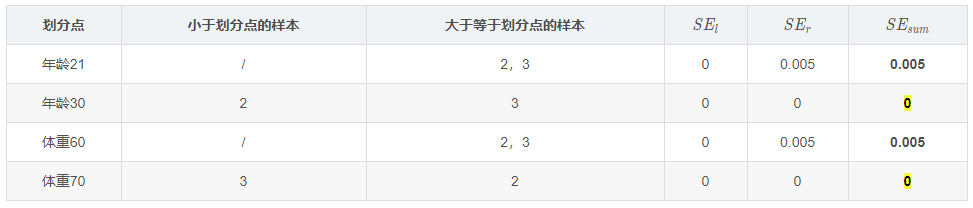
image.png
可以选择选择年龄30划分，第一棵树长这个样子：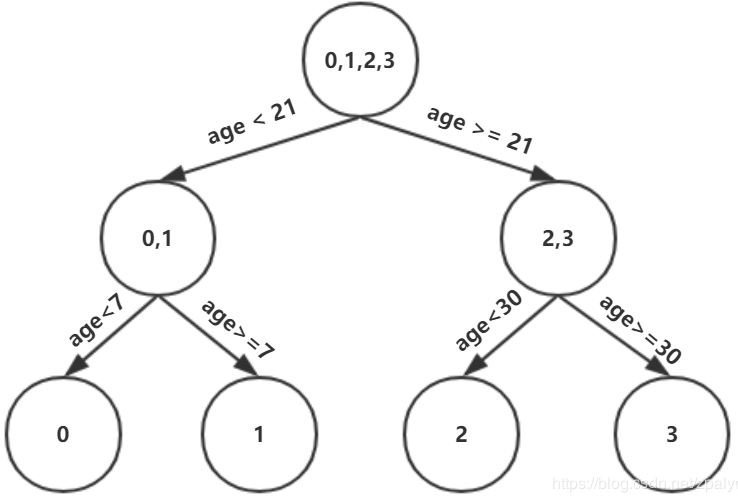
image.png

（5）对节点打分

上面这棵树深度满足了设置，还需要做一件事情，给这每个叶子节点打分（CART树回归）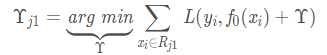
image.png
这里和上面初始化学习器是一个道理，平方损失，求导，令导数等于零，这个地方的标签值不是原始的y，而是本轮要拟合的残差y-f(x)，γ就是标签值的均值（这里恰好每个叶子节点只有一个样本），这样可以将树的结构表示如下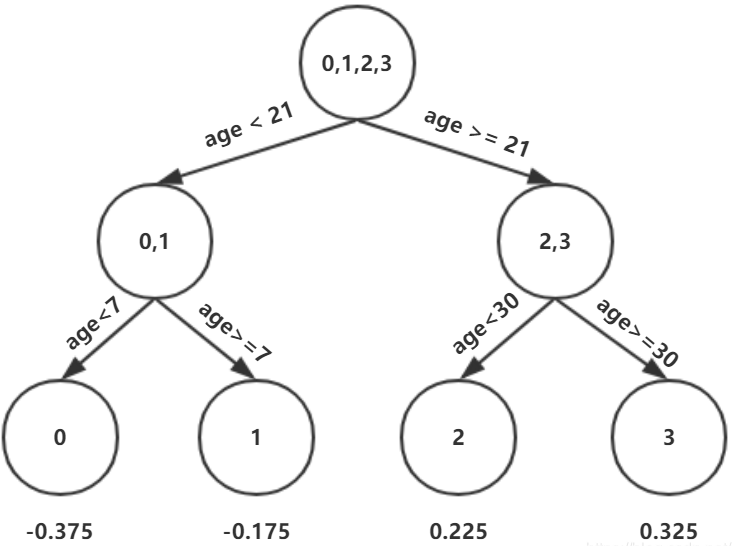
image.png

（6）下一棵树

对于样本0，可以计算出预测的身高：1.475+0.1（-0.375）=1.4375，此时的残差=真实值-预测值=1.1-1.4375 =-0.3375，有了这个残差之后，又可以进行下一轮的树划分，得到的结果如下。
**这里的0.1是学习率，防止仅仅只用很少的几棵树就达到停止条件，这样会欠拟合。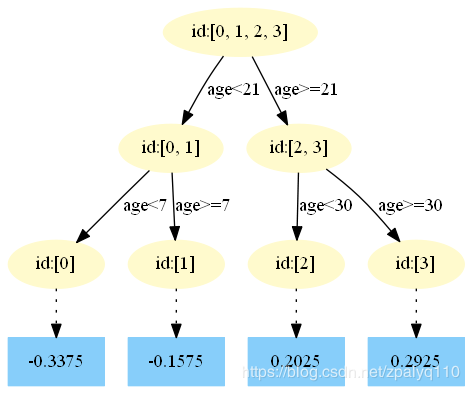
image.png
由于定义的是一共有5颗数，此时还没有完，可以得到第3，4，5棵数。最终的函数表达式为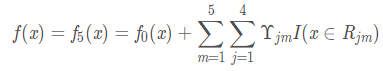
image.png
对于第4颗数，它的预测结果为
image.png