ES 是基于 Lucene 的全文检索引擎,它会对数据进行分词后保存索引,擅长管理大量的数据,相对于 MySQL 来说不擅长经常更新数据及关联查询。这篇文章就是为了进一步了解一下它,到底是如何做到这么高效的查询的。
在学习其他数据库的时候我们知道索引是一个数据库系统极其重要的部分,它直接决定着查询的效率。ES之所以快,是因为其底层的Lucene采用倒排索引的方式,并且还有很多的优化点,
倒排索引
何谓倒排索引?
——先看正排索引,如下表: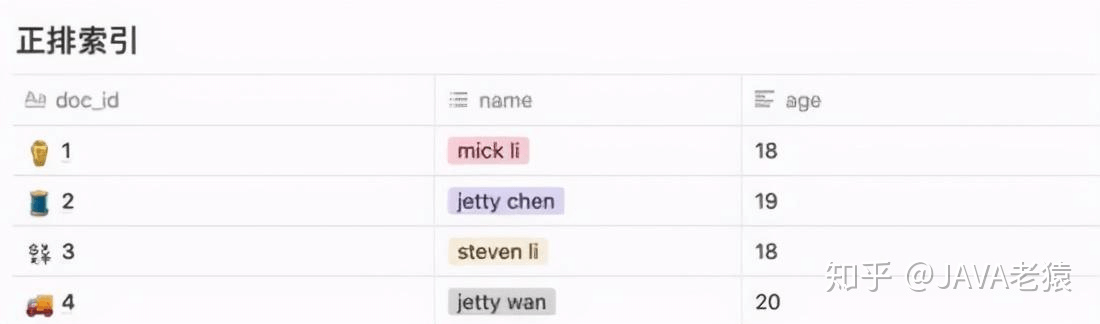
上图就是一个简单的正排索引。即将doc_id作为主键索引key,去查询到对应的一行数据value。
而倒排索引就有些反其道而行之的概念了。我们先将每句话按照单词分成一个一个的,而后看看对应的doc_id有哪些: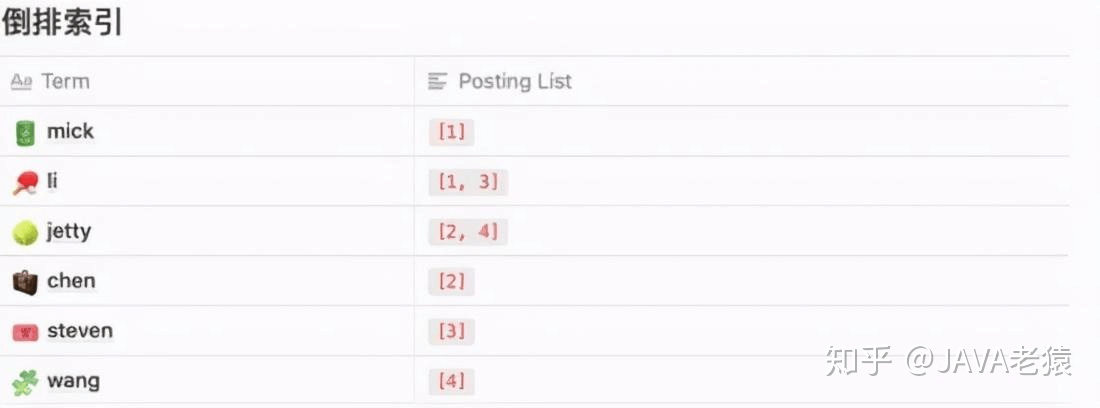
当要查询 包含 li 的数据时,只需要通过这个索引结构查询到 Posting List 中所包含的数据,再通过映射的方式查询到最终的数据。
就相当于由value去找出可能的key,再利用key去获取完整的数据。这种索引结构就是所谓的倒排索引。
虽然上面这种方式,可以实现查询数据到Position LIst(理解为行id等都可以)的快速查找,但是,使用什么数据结构来存储Term呢?
Term Index
我们将所有 Term 合并在一起就是一个 Term Dictionary,也可以叫做单词词典。英文的分词相对简单,只需要通过空格、标点符号将文本分隔便能拆词,中文则相对复杂,但也有许多开源工具做支持。
现在要解决一个问题,我们如何保存Term呢?
比如现在有多个Term:
Carla,Sara,Elin,Ada,Patty,Kate,Selena
我们需要从中找出某个特定的Term,只能遍历,那么时间复杂度平均为O(n),这在单词数众多的时候很慢,而如果我们能够按照某种规则将其排序,那么利用二分查找的方式就可以将时间复杂度降到O(logN):
Ada,Carla,Elin,Kate,Patty,Sara,Selena
当我们的文本量巨大时,分词后的 Term 也会很多,这样一个倒排索引的数据结构如果存放于内存那肯定是不够存的,但如果像 MySQL 那样存放于磁盘,去访问磁盘获取数据效率也没那么高。
为了尽可能减小磁盘IO的次数,所以我们可以使用一个折中的方式——既然内存中无法放入整个Term Dictionary,那我就为Term Dictionary创建一个索引Term Index,将这个索引放到内存里。
term index 有点像一本字典的大的章节表。比如:
A 开头的 term ……………. Xxx 页
C 开头的 term ……………. Yyy 页
E 开头的 term ……………. Zzz 页
如果所有的 term 都是英文字符的话,可能这个 term index 就真的是 26 个英文字符表构成的了。
但是实际的情况是,term 未必都是英文字符,term 可以是任意的 byte 数组。而且 26 个英文字符也未必是每一个字符都有均等的 term,比如 x 字符开头的 term 可能一个都没有,而 s 开头的 term 又特别多。实际的 term index 是一棵 trie 树: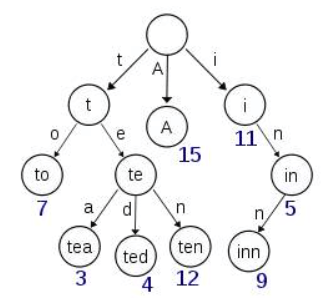
例子是一个包含 “A”, “to”, “tea”, “ted”, “ten”, “i”, “in”, 和 “inn” 的 trie 树。这棵树不会包含所有的 term,它包含的是 term 的一些前缀。通过 term index 可以快速地定位到 term dictionary 的某个 offset,然后从这个位置再往后顺序查找。再加上一些压缩技术( Finite State Transducers) term index 的尺寸可以只有所有 term 的尺寸的几十分之一,使得用内存缓存整个 term index 变成可能。整体上来说就是这样的效果。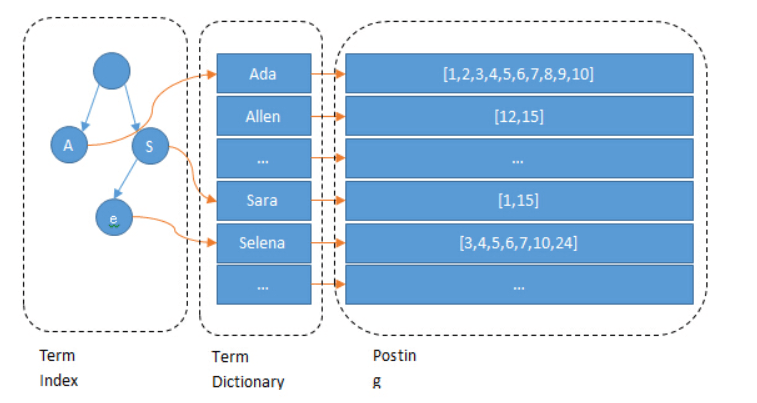
现在我们可以回答“为什么 Elasticsearch/Lucene 检索可以比 mysql 快了”。 Mysql 只有 term dictionary 这一层,是以 b-tree 排序的方式存储在磁盘上的。检索一个 term 需要若干次的 random access 的磁盘操作。而 Lucene 在 term dictionary 的基础上添加了 term index 来加速检索,term index 以树的形式缓存在内存中。从 term index 查到对应的 term dictionary 的 block 位置之后,再去磁盘上找 term,大大减少了磁盘的 random access 次数。
于是整个搜索过程就变成了先找到对应Term在Term Dictionary中的索引,而后再根据索引去查找Postion List,也就获取到了最终的数据。即下面这个流程: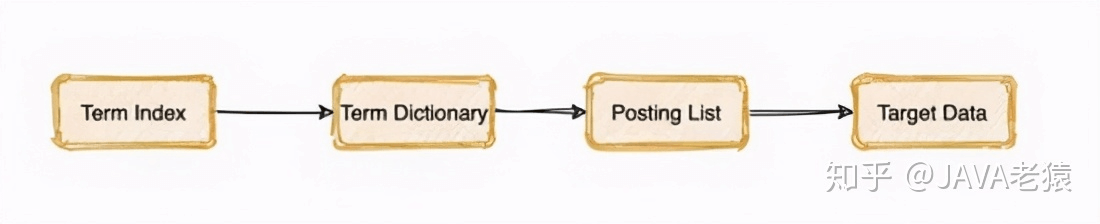
FST
实际上,Lucene 内部的 Term Index 是用的「变种的」trie树,即 FST 。那么相比于传统的Trie树,有什么改进?
trie树只共享了前缀,而 FST 既共享前缀也共享后缀,更加的节省空间。
FST使用FSM(Finite State Machines)作为数据结构。
FSM(Finite State Machines)有限状态机: 表示有限个状态(State)集合以及这些状态之间转移和动作的数学模型。其中一个状态被标记为开始状态,0个或更多的状态被标记为final状态。 一个FSM同一时间只处于1个状态。FSM很通用,可以用来表示多种处理过程,下面的FSM描述了《小猫咪的一天》。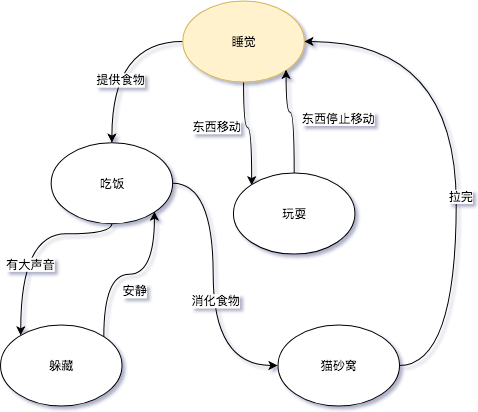
其中“睡觉”或者“吃饭”代表的是状态,而“提供食物”或者“东西移动”则代表了转移。
以上只是一个现实中的例子,下面我们来看如何实现一个Ordered Sets,和Ordered Map结构。最后,再来考虑如何实现一个FST。
Ordered Sets
Ordered Sets是一个有序集合。通常一个有序集合可以用二叉树、B树实现。无序的集合使用hash table来实现.。这里,我们用一个确定无环有限状态接收机(Deterministric acyclic finite state acceptor, FSA)来实现。
FSA是一个FSM(有限状态机)的一种,特性如下:
- 确定:意味着指定任何一个状态,只可能最多有一个转移可以访问到。
- 无环: 不可能重复遍历同一个状态
- 接收机:有限状态机只“接受”特定的输入序列,并终止于final状态。
下面来看,我们如何来表示只有一个key:“jul”的集合。FSA是这样的:
当查询这个FSA是否包含“jul”的时候,按字符依序输入。
- 输入j,FSA从0->1
- 输入u, FSA从1->2
- 输入l,FSA从2->3
这个时候,FSA处于final状态3,所以“jul”是在这个集合的。
设想一下如果输入“jun”,在状态2的时候无法移动了,就知道不在这个集合里了。
设想如何输入“ju”, 在状态2的时候,已经没有输入了。而状态2并不是final状态,所以也不在这个集合里。
值得指出的是,查找这个key是否在集合内的时间复杂度,取决于key的长度,而不是集合的大小。
现在往FSA里再加一个key. FSA此时包含keys:”jul”和“mar”。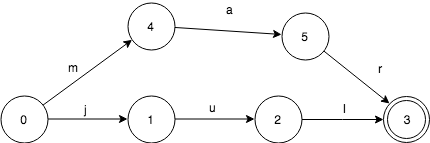
start状态0此时有了2个转移:j和m。
因此,输入key:“mar”,首先会跟随m来转移。 final状态是“jul”和“mar”共享的。这使得我们能用更少的空间来表示更多的信息。
当我们在这个FSA里加入“jun”,那么它和“jul”有共同的前缀“ju”: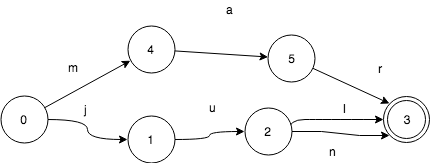
这里变化很小,没有增加新的状态,只是多了一个转移而已。
下面来看一下由“october”,“november”,”december”构成的FSA.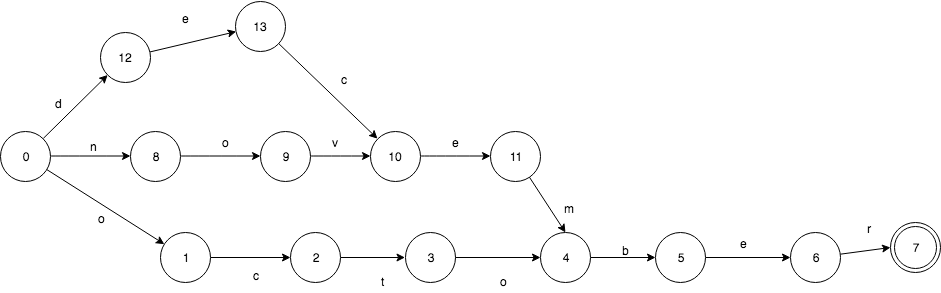
它们有共同的后缀“ber”,所以在FSA只出现了1次。 其中2个有共同的后缀“ember”,也只出现了1次。
那么我们如何来遍历一个FSA表示的所有key呢,我们以前面的”jul”,“jun”,”mar”为例:
遍历算法是这样的(DFS):
- 初始状态0, key=””
- ->1, key=”j”
- ->2, key=”ju”
- ->3, key=”jul”, 找到jul
- 2<-, key=”ju”
- ->3, key=”jun”, 找到jun
- 2<-, key=”ju”
- 1<-, key=”j”
- 0<-, key=””
- ->4, key=”m”
- ->5, key=”ma”,
- ->3, key=”mar”,找到mar
这个算法时间复杂度O(n),n是集合里所有的key的大小, 空间复杂度O(k),k是结合内最长的key字段length。
Map
Ordered maps就像一个普通的map,只不过它的key是有序的。我们来看一下如何使用确定无环状态转换器(Deterministic acyclic finite state transducer, FST)来实现它。
FST是也一个有限状态机(FSM),具有这样的特性:
- 确定:意味着指定任何一个状态,只可能最多有一个转移可以遍历到。
- 无环: 不可能重复遍历同一个状态
- transducer:接收特定的序列,终止于final状态,同时会输出一个值。
FST和FSA很像,给定一个key除了能回答是否存在,还能输出一个关联的值。
下面来看这样的一个输入:“jul:7”, 7是jul关联的值,就像是一个map的entry.
这和对应的有序集合基本一样,除了第一个0->1的转换j关联了一个值7. 其他的转换u和l,默认关联的值是0,这里不予展现。
那么当我们查找key:“jul”的时候,大概流程如下:
- 初始状态0
- 输入j, FST从0->1, value=7
- 输入u, FST从1->2, value=7+0
- 输入l,FST从2->3, value=7+0+0
此时,FST处于final状态3,所以存在jul,并且给出output是7.
我们再看一下,加入mar:3之后,FST变成什么样: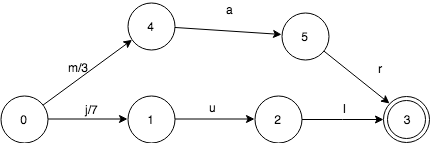
同样的很简单,需要注意的是mar自带的值3放在了第1个转移上。这只是为了算法更简单而已,事实上,可以放在其他转移上。
如果共享前缀,FST会发生什么呢?这里我们继续加入jun:6。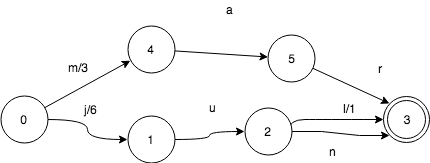
和sets一样,jun和jul共享状态3, 但是有一些变化。
- 0->1转移,输出从7变成了6
- 2->3转移,输入l,输出值变成了1。
这个输出变化是很重要的,因为他改变了查找jul输出值的过程。
- 初始状态0
- 输入j, FST从0->1, value=6
- 输入u, FST从1->2, value=6+0
- 输入l,FST从2->3, value=6+0+1
最终的值仍旧是7,但是走的路径却是不一样的。
那查找jun是不是也是正确的呢?
- 初始状态0
- 输入j, FST从0 -> 1, value=6
- 输入u,FST从1 -> 2, value=6+0
- 输入n,FST从2 -> 3, value=6+0+0
从上可知,jun的查询也是正确的。FST保证了不同的转移有唯一的值,但同时也复用了大部分的数据结构。
实现共享状态的关键点是:每一个key,都在FST中对应一个唯一的路径。因此,对于任何一个特定的key,总会有一些value的转移组合使得路径是唯一的。我们需要做的就是如何来在转移中分配这些组合。
key输出的共享机制同样适用于共同前缀和共同后缀。比如我们有tuesday:3和thursday:5这样的FST:
2个key有共同的前缀t,共同后缀sday。关联的2个value同样有共同的前缀。3可以写做3+0,而5可以写作:3+2。 这样很好的让实现了关联value的共享。
上面的这个例子,其实有点简单化,并且局限。假如这些关联的value并不是int呢? 实际上,FST对于关联value(outputs)的类型是要求必须有以下操作(method)的。
- 加(Addition)
- 减 (Subtraction)
- 取前缀 (对于整数来说,就是min)
构建FST
TRIE树的构建
TRIE可以看做是一个FSA,唯一的一个不同是TRIE只共享前缀,而FSA不仅共享前缀还共享后缀。
假设我们有一个这样的Set: mon,tues,thurs。FSA是这样的: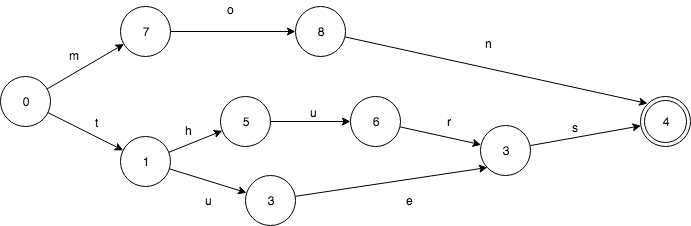
相应的TRIE则是这样的,只共享了前缀。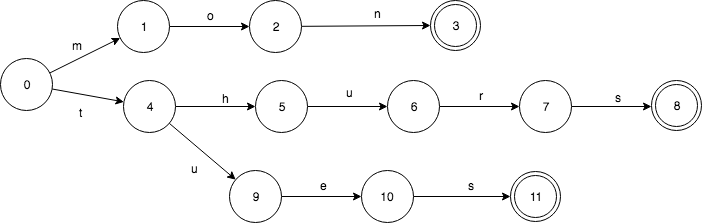
TRIE有重复的3个final状态3,8,11. 而8,11都是s转移,是可以合并的。
构建一个TRIE树是相当简单的。插入1个key,只需要做简单的查找就可以了。如果输入先结束,那么当前状态设置为final;如果无法转移了,那么就直接创建新的转移和状态。不要忘了最后一个创建的状态设置为final就可以了。
FST的构建
构建FST在很大程度上和构建FSA是一样的,主要的不同点是,怎么样在转移上放置和共享outputs。
仍旧使用前面提到的例子,mon,tues和thurs,并给他们关联相应的星期数值2,3和5.
从第1个key, mon:2开始:
这里虚线代表,在后续的insert过程中,FST可能有变化。
需要关注的是,这里只是把2放在了第1个转移上。技术上说,下面这样分配也是正确的。
只不过,把output放在靠近start状态的算法更容易写而已。
下面继续把thurs:5插入: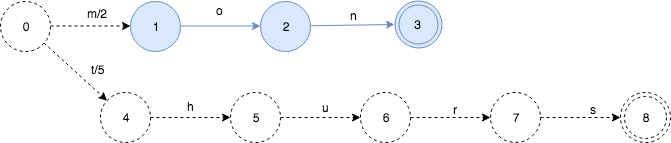
就像FSA的insert一样,插入thurs之后,我们可以知道FST的mon部分(蓝色)就不会再变了。
由于mon和thurs没有共同的前缀,只是简单的2个map中的key. 所以他们的output value可以直接放置在start状态的第1个转移上。
下面,继续插入tues:3,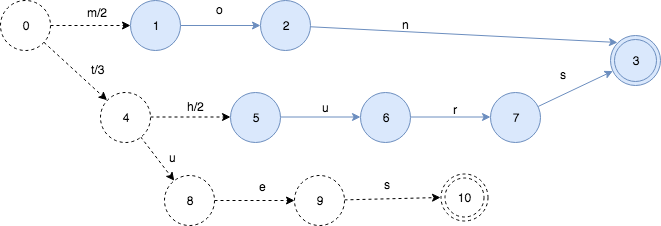
这引起了新的变化。有一部分被冻住了,并且知道以后不会再修改了。output value也出现了重新的分配。因为tues的output是3,并且tues和thurs有共同的前缀t, 所以5和3的prefix操作得出的结果就是3. 状态0->状态4的value被分配为3,状态4->状态5设置为2。
我们再插入更多的key, 这次插入tye:99看发生什么情况: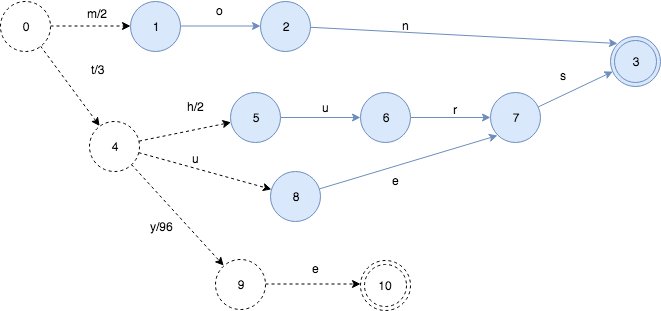
插入tye,导致”es”部分被冻住,同时由于共享前缀t, 状态4->状态9的输出是99-3=96。
最后一步,结束了,再执行一次冻住操作。
最终的FST长这样: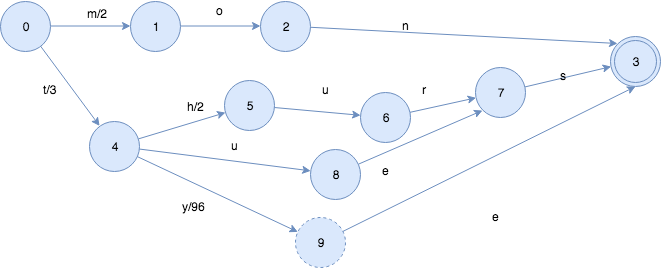
Lucene
咱们之前讲的处理分词,构建倒排索引,等等,都是这个叫lucene的做的。那么能不能说这个lucene就是搜索引擎呢?
还不能。lucene只是一个提供全文搜索功能类库的核心工具包,而真正使用它还需要一个完善的服务框架搭建起来的应用。
好比lucene是类似于发动机,而搜索引擎软件(ES,Solr)就是汽车。
目前市面上流行的搜索引擎软件,主流的就两款,elasticsearch和solr,这两款都是基于lucene的搭建的,可以独立部署启动的搜索引擎服务软件。

