- 001.赋值运算符函数
- 002.实现单例模式
- 003.数组中重复的数字
- 004.二维数组的查找
- 005.替换空格
- 006.从尾到头打印链表
- 007.重建二叉树
- 008.二叉树的下一个节点
- 009.用两个栈实现队列
- 010.斐波拉契数列
- (待补充,几种排序算法!必须会!!)
- 011.旋转数组的最小数字
- 012.矩阵中的路径
- 013.机器人的运动范围
- ">014.**剪绳子**

- 015.**二进制中1的个数**
- 016.**数值的整数次方**
- 017.*打印从1到最大的n位数(*)
- 018.**删除链表的节点**
- 019.正则表达式匹配
- 020.表示数值的字符串
- 021.使奇数位于偶数前面(参考第二种题解)
- 022.链表中倒数第k个节点
- 023.链表中环的入口节点
- 024.反转链表
- 025.合并两个排序的链表
- 026.树的子结构
- 027.二叉树的镜像
- 028.对称的二叉树
- 029.顺时针打印矩阵
- 030.包含min函数的栈
- 031.栈的压入、弹出序列
- 032.从上到下打印二叉树
- 033.二叉搜索树的后序遍历序列
- 034.二叉树中和为某一值的路径
- 035.复杂链表的复制
- 036.二叉搜索树和双向链表
- 037.序列化二叉树(重点)
- 038.字符串的排列
- 039.次数超过一半的数字
- 040.最小的K个数
- 041.数据流中的中位数
- 042.连续子数组的最大和
- include
max_element(dp.begin(),dp.end())
min_element(dp.begin(),dp.end())
返回的本来是迭代器的值,解引用即可拿到最大最小值;
第二种,或是探寻数组中数字规律。
以[-2,1,-3,4,-1,2,1,-5,4]为例:
初始化结果为0,最大值为0,因为-2小于0,直接跳过从下一位开始;
接着+1,结果为1,最大值暂时更新为1,接着-3,结果小于0,直接抛弃结果从+4开始重新计算。
捋一捋逻辑:
两个变量:当前结果以及当前最大值;
加一个数之后,如果结果大于最大值,则更新最大值,否则最大值不变。
如且如结果小于0,直接跳到下一位重新加(当前结果置0);
代码就出来了:
int maxSubArray(vector& nums) {
int curRes=0;
int curMax=INT_MIN;
for(auto value:nums){
curRes+=value;//依次累加
if(curRes>curMax)//最大值可能会更新
{
curMax=curRes;
}
if(curRes<=0)//连续子数组和小于0
{
curRes=0;
}
}
return curMax;
} - 043.1~n整数中1出现的次数
- 044.数字序列中某一位的数字
- 045.把数组排成最小的数
- 046.*把数字翻译成字符串**
- 047.礼物的最大价值
- 048.最长不含重复字符的子字符串
- 049.丑数
- 050.第一个只出现一次的字符
- 051.数组中的逆序对
- 052.两个链表的第一个公共节点
- 053.在排序数组中查找数字
- 054.**二叉搜索树的第K大节点**
- 055.**二叉树的深度**
- 056.**数组中出现两次**
- 057.**和为s的数字**
- 058.**反转字符串**
- 059.**队列的最大值**
- 060.n个骰子的点数
- 061.扑克牌中的顺子
- 062.圆圈中最后剩下的数字
- F063.股票的最大利润
- 064.求1+2+….n
- 065.不用加减乘除做加法
- **066.构建乘积数组
- 067.字符串转换为整数
- 068.树中两个节点的最近公共祖先
- 二叉树中和为某一值的路径
001.赋值运算符函数
有一个类声明如下,请重载其赋值运算符:
class CMyString{public:CMyString(char *p = nullptr);CMyString(const CMyString& str);~CMyString();private:char *m_pData;}
即重载赋值运算符,完成str1=str2=str3···等赋值操作,对于这个数组结构而言,就是传递m_pData指针,所以题目考察的就是如何安全简洁地实现指针的复制。
补充:赋值/拷贝重载函数
默认使用是浅拷贝,也就是说将该对象的内存原封不动地挪动到新对象的内存中,因此对于含有指针的类,这种方式很有可能造成有多个指针指向同一块空间,在析构时候同一块空间析构多次导致崩溃,因此需要实现深拷贝来完成拷贝。
这道题有四个要点:
- 重载运算符是怎么重载的?
- 返回自身的引用(this)(为了实现连等操作);
- 注意内存消耗以及内容的不变性(有时由于内存错误会造成原数据丢失,即异常安全性);
- 判断是不是同一个实例(比如a==a);
先给出一个初代版本:
CMyString& CMyString::operator=(const CMyString& other){if (this != &other){// 析构了对象,但是其对应的内存地址起始还在delete[] m_pData;// 其实可以直接new,但是delete之后// 将指针赋值为nullptr// 是C++程序员的基本操作m_pData = nullptr;// 之所以用strlen是因为如果用size// 数组就退化为指针了哦m_pData = new char[strlen(other.m_pData) + 1];// 前面是目的strcpy(m_pData, other.m_pData);}return *this;}
strlen所作的是一个计数器的工作,它从内存的某个位置(可以是字符串开头,中间某个位置,甚至是某个不确定的内存区域)开始扫描,直到碰到第一个字符串结束符’\0’为止,然后返回计数器值(长度不包含’\0’)。
上述代码是先释放了原本的内存空间,而后再开辟新的,要是···新的内存不够呢?出现异常呢?那以前的数据不就丢失了么?
因此我们需要考虑出现异常如何解决。
改进版本:
CMyString& CMyString::operator=(const CMyString& other){if (this != &other){//先分配空间char *pTemp = new char[strlen(other.m_pData) + 1];strcpy(pTemp, other.m_pData);//分配成功后再释放原来的内存delete[] m_pData;m_pData = nullptr;m_pData = pTemp;}return *this;}
还可利用临时对象自动构造析构的特性的实现方法:
class mystring{public:mystring(char* Pdata);mystring(const mystring& str);~mystring();mystring& operator=(const mystring&str){/**以下实现了操作的异常安全性,并释放原有的内存,因为strTemp会自动析构**/if(&str!=this){mystring strTemp(str);char* pTemp=strTemp.m_pData;strTemp.m_data=m_pData;m_pData=pTemp;// 上面的代码,其实就是// swap(m_pData,strTemp.m_data);}return *this;};private:char* m_data;}
1.class 与struct有什么区别? 答:(其实这两者都可以用来定义成员变量、成员函数等等,都可以声明public和private)区别就在于struct的默认权限是public,而class是private;另一个区别为,class可用于声明类模板,而struct不可以; 2.C++中对象的建立可以在堆和栈上。分别为静态建立和动态建立的方式,构建堆上的对象时一般使用new关键字,而对象的指针在栈上。使用new在堆上构建的对象需要主动的delete销毁。 C++对象可以在堆或栈中,函数的传参可以是对象(对象的拷贝),或是对象的指针。
002.实现单例模式
单例模式,全局只能有其一个对象。(参考链接:单例模式详解)
由于全局只能有一个实例对象,那么构造函数必须为私有,这样就禁止了他人创造实例;
最好将这个实例对象在私有变量里作为一个静态私有变量;
如果私有化析构函数会怎样? 答:https://www.cnblogs.com/hu983/p/5501535.html。 只能在堆上用new创建,而不能在栈上自动创建并析构。
C++实现
简单懒汉模式;多线程不安全(主要在==null判断)
class singleton{public:~singleton();//必须是静态的,因为静态成员函数才可以实现在无类实体时去访问构造函数static singleton* getInstance(){if(m_Pinstance==null){m_Pinstance=new singleton();}return m_Pinstance;}private:singleton();singleton(singleton&)=delete;//禁止拷贝构造singleton& operator=(const singleton&)=delete;//禁止赋值构造static singleton* m_Pinstance;//注意命名的规范性}singletopn:: m_Pinstance=null;//静态成员不能在类内初始化
双判断同步锁的懒汉模式
class singleton{public:~singleton();//必须是静态的,因为静态成员函数才可以实现在无类实体时去访问构造函数static singleton* getInstance(){if(m_Pinstance==null){std::lock_guard<std::mutex> lk(m_mutex);if(m_Pinstance==null){m_Pinstance=new singleton();}}return m_Pinstance;}private:singleton();singleton(singleton&)=delete;//禁止拷贝构造singleton& operator=(const singleton&)=delete;//禁止赋值构造static singleton* m_Pinstance;//注意命名的规范性static std::mutex m_mutex;//实现互斥}singleton:: m_Pinstance=null;//静态成员不能在类内初始化std::mutex singleton::m_mutex;//静态成员不能在类内初始化
想想为什么一个不只用一个判断呢? 提高系统效率,免得每次都去获取锁
饿汉模式就是线程安全的,因为编译时就初始化了:
class singleton{protected :singleton(){}private :static singleton* p;public :static singleton* initance();};// 因为编译完成就初始化了singleton* singleton::p = new singleton;singleton* singleton::initance(){return p;}
还可以这样实现,利用C++11局部静态变量特性的方式:
// 局部静态变量class Singleton{public:// 使用指针而不是引用是为了避免拷贝构造函数进行拷贝// Singleton single = Singleton::getInstance();static Singleton* getInstance(){static Singleton instance;return &instance;}//局部静态变量在构造时,其他线程必须等待;private:Singleton(){std::cout << "局部静态方式" << std::endl;}// 如果需要getInstance 返回引用,Singleton(Singleton const & )=delete;Singleton& operator = (const Singleton&)=delete;};
静态局部变量存放在内存的全局数据区。 函数结束时,静态局部变量不会消失,每次该函数调用时,也不会为其重新分配空间。它始终驻留在全局数据区,直到程序运行结束。静态局部变量只在定义它的函数中可见。
Java实现
饿汉模式(静态常量),缺点是没有使用lazy loading,如果从始至终都没有使用这个类,那就浪费了:
public class SingleObject {//创建 SingleObject 的一个对象private static final SingleObject instance = new SingleObject();//让构造函数为 private,这样该类就不会被实例化private SingleObject(){}//获取唯一可用的对象public static SingleObject getInstance(){return instance;}public void showMessage(){System.out.println("Hello World!");}}
饿汉模式(静态代码块),跟上面一样,都是在类加载的时候完成变量的构造:
public class Singleton{private static Singleton instance;static{instance=new Singleton();}private Singleton(){}public static Singleton getInstance(){return instance;}}
懒汉模式,双重检查:
public class Singleton{private static volatile Singleton singleton;private Singleton(){}public static Singleton getInstance(){if(singleton==null){synchronized(Singleton.class){if(singleton==null){singleton=new Singleton();}}}return singleton;}}
懒汉模式,静态内部类:
这种方式跟饿汉式方式采用的机制类似,但又有不同。两者都是采用了类装载的机制来保证初始化实例时只有一个线程。不同的地方在饿汉式方式是只要Singleton类被装载就会实例化,没有Lazy-Loading的作用,而静态内部类方式在Singleton类被装载时并不会立即实例化,而是在需要实例化时,调用getInstance方法,才会装载SingletonInstance类,从而完成Singleton的实例化。
public class Singleton{private Singleton(){}private static class SingletonInstance{private static final Singleton INSTANCE = new Singleton();}public static Singleton getInstance(){return SingletonInstance.INSTANCE;}}
补充:数组地址与指针
在C/C++中,数组和指针既相互关联又有区别。
声明数组时,数组名即是一个指针,该指针指向数组的第一个元素。由于C/C++没有记录数组的大小,因此在用指针访问数组中的元素时,确保不会越界。
下面这个例子可以了解数组和指针的区别:
int GetSize(int data[]){return sizeof(data);}int main(){int data1[]={1,2,3,4,5};int size1=sizeof(data1);int *data2=data1;int size2=sizeof(data2);int size3=GetSize(data1);printtf("%d,&d,&d",size1,size2,size3);}
最后的结果应该为:54=20; 8(64位机);8(64位机);
一是声明数组之后,数组名就代表整个数组;但在进行参数传递时,数组名会进行退化变成一个普通的指针,而不是代表数组(这是C语言为了防止直接拷贝数组造成栈溢出的解决方式);
*数组的首地址是常量,不可更改,指针保存的地址是变量,可以更改
PS:vector在VS下是1.5倍扩大,GCC下是2倍扩大; PS:C++中虽然可以进行数组的引用传递,但是必须数组大小一致,扩展性极差;
003.数组中重复的数字

法一、Hash表(空间复杂度O(n)),这里还不如数组,因为hash空间大一些;
法二、先排序再遍历相邻两个数是否相等,时间复杂度O(nlogn);
法三、鸽巢原理。结合题目长度为n,范围在0-n-1,则重复的数字必然占据了其他人的位置(比如1应该在1号位,但是被第二个0占据了),那就不停的交换,直到发现某一个坑位被占据了,或者所有位置都正确位置(这样不停交换的结果是所有位置会逐渐有序)。
C/C++
classSolution {public:int findRepeatNumber(vector<int>& nums){for(int i = 0; i < nums.size(); ++i){while(nums[i] != i) //当前元素不等于下标{// 转换之前,先看看那个坑位是不是被占据了// 被占据了,说明找到重复数if(nums[i] == nums[nums[i]])return nums[i];// C++<algorithm>里包括的swap(nums[i],nums[nums[i]]);}}return-1;}};
golang
type CQueue struct {stk_in []intstk_out []int}func Constructor() CQueue {return CQueue{stk_in:make([]int,0),stk_out:make([]int,0),}}func (this *CQueue) AppendTail(value int) {this.stk_in = append(this.stk_in,value)}func (this *CQueue) DeleteHead() int {if len(this.stk_out)!=0{res := this.stk_out[len(this.stk_out)-1]this.stk_out = this.stk_out[:len(this.stk_out)-1]return res}else{if len(this.stk_in)==0{return -1}for ;len(this.stk_in)!=0;{this.stk_out=append(this.stk_out,this.stk_in[len(this.stk_in)-1])this.stk_in = this.stk_in[:len(this.stk_in)-1]}res := this.stk_out[len(this.stk_out)-1]this.stk_out = this.stk_out[:len(this.stk_out)-1]return res}}

法一、复制一个数组,在新数组上进行上一题的操作,空间复杂度N可以使用hash表;
法二、既然题目是不修改数组,那么重点就在于如何用1的空间实现查找.重复元素会造成“二分查找”时两边的数量不相等(这是一个伪二分,需要统计区间内数目的,所以时间复杂度是nlogn);
因此,我们把从1~n的数字从中间的数字m分为两部分,前面一半为1~m,后面一半为m+1~n。如果1~m的数字的数目超过m,那么这一半的区间里一定包含重复的数字;否则,另一半m+1~n的区间里一定包含重复的数字。我们可以继续把包含重复数字的区间一分为二,直到找到一个重复的数字。这个过程和二分查找算法很类似,只是多了一步统计区间里数字的数目。
bool getDuplication(const int* numbers, int length, int& num){if (numbers == NULL || length <= 0)//判断输入是否对return false;// 这一环节可要可不要// 判断是否满足题目条件/*for (int i = 0; i < length; i++){if (numbers[i] < 1 || numbers[i] > length)return false;}*/// 这个start和end不是区间大小// 而是数值的范围int start = 1, end = length - 1;while (end >= start){// 一个trick 防止溢出int middle = ((end - start) >> 1) + start;int count = counter(numbers, length, start, middle);//查找落在二分左区间内个数if (start == end)//二分不动了,停止,判断这个值count值{// 左右边界都相等了,结果count还大于1// 那必然是重复了啊!if (count > 1){num = start;return true;}elsebreak;}if (count > (middle - start) + 1)//如果落在左区间的个数大于区间范围,则这里面一定有重复,否则就去右区间看看end = middle;elsestart = middle + 1;}return false;}int counter(const int* numbers, int length, int start, int middle){int count = 0;if (numbers == NULL || start > middle || start < 0)return count;for (int i = 0; i < length; i++){if (numbers[i] >= start&&numbers[i] <= middle)count++;}return count;}
004.二维数组的查找

如果只是选取矩形,分析比较复杂,那就从右上角开始分析: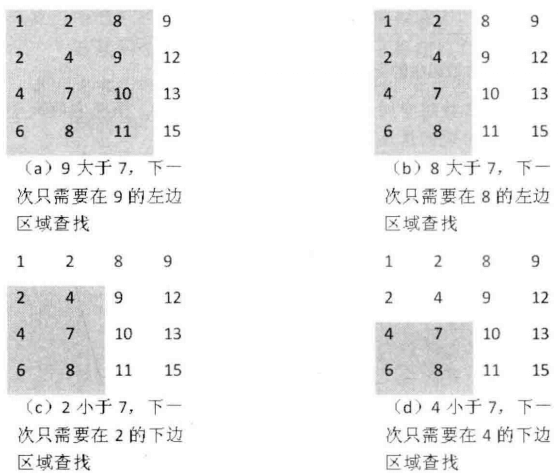
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {if(matrix.size()==0)return false;rows=matrix.size();cols=matrix[0].size();if(rows>0&&cols>0){int row=0;int col=cols-1;while(row<rows&&col>=0){if(matrix[row][col]==target)return true;else if(matrix[row][col]>target)col--;elserow++;}}return false;}
补充:C/C++中的字符串
为了节省内存,C/C++通常把常量字符串放在单独的一个内存区域。
当几个指针赋值给相同的常量字符串,它们实际会指向相同的内存地址。但若是用常量字符串初始化数组,它们是分别分配的新内存,地址自然不同。
005.替换空格

方法:双指针,拓展字符串,从尾到头;如果从头开始移动字符串需要n^2的时间复杂度,且需要一直进行字符串的拷贝操作,浪费内存;如果利用双指针,从后面往前开始,则只需要n的时间复杂度。
class Solution {int before, after;public:string replaceSpace(string s) {if (s.size() == 0)return s;string replace = "%20";int countSpace = 0;before = s.size() - 1;//1 计算空格数目for (int i = 0; i<s.size(); i++) {if (s[i] == ' ')countSpace++;}//2.扩大字符串数目//s.insert(before+1, countSpace * 2, '0');s.resize(s.size()+countSpace*2,'0');//3.指向新字符串的末尾after = s.size()-1;//4.再次遍历数组,遇到空格加入%20while (before >= 0) {if (s[before] == ' ') {s[after] = '0';after--;s[after] = '2';after--;s[after] = '%';after--;before--;}else {s[after] = s[before];before--;after--;}}return s;}};
补充:链表

之所以是指针的指针,是为了防止当该链表为空的时候一旦退出这个函数,该链表仍旧为空;
006.从尾到头打印链表

法一、用栈
class Solution {public:vector<int> reversePrint(ListNode* head) {if(head==NULL)return {};//或者vector<int>(0)stack<int>tempAns; //利用栈来实现从尾到头打印链表vector<int>Ans;while(head!=NULL){tempAns.push(head->val);head=head->next;}while(!tempAns.empty()){Ans.push_back(tempAns.top());tempAns.pop();}return Ans;}};
法二、递归操作
class Solution {vector<int> res;public:vector<int> reversePrint(ListNode* head) {if(head==NULL)return {};//或者vector<int>(0)dfs(head);return res;}void dfs(ListNode* head){if(head==NULL)return;dfs(head->next);res.push_back(head->val);return;}};
补充·树(前序、中序、后序的迭代)
每一种都有递归和循环(迭代,迭代的时候需要显式地将这个栈模拟出来)两种实现方式,所以一共有六种方式(实现方式还有morris方法,在这不赘述)。如下所示:
前序·递归:
前序·迭代
PS:中序跟后序的差别就在于顺序而已;(递归太简单,只展示迭代)
中序·迭代:
区别只在于中序遍历是弹出时获取节点数据。
后序·迭代:
或者:后序遍历整体与前中序遍历过程相似。但要注意,这时对于父节点的访问输出,需要在其右子树遍历完成的前提下进行。所以不能像前中序遍历一样,在遍历完左子树后,就直接出栈。我们需要利用这个未出栈的栈顶元素去获取右子树,在遍历完右子树后,就可以出栈,并对此节点进行访问输出。
这里我们需要使用一个标记,以区分是从左子树取栈还是从右子树出栈:(如图所示)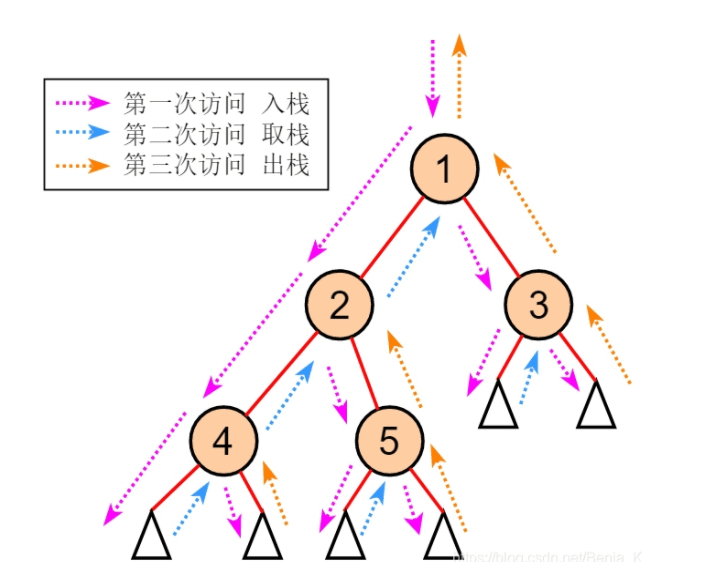
从当前节点开始遍历:
\1. 若当前节点存在,就存入栈中,并且置节点flag为1(第一次访问),然后访问其左子树;
\2. 直到当前节点不存在,需要回退,这里有两种情况:
1)当栈顶节点flag为1时,则表明是从左子树回退,这时需置栈顶节点flag为2(第二次访问),然后通过栈顶节点访问其右子树(取栈顶节点用,但不出栈)
2)当栈顶节点flag为2时,则表明是从右子树回退,这时需出栈,并取出栈节点做访问输出。(需要注意的是,输出完毕需要置当前节点为空,以便继续回退。具体可参考代码中的p = NULL)
\3. 不断重复12,直到当前节点不存在且栈空。
void postOrder(TreeNode *T){TreeNode *stack[15];int top = -1;int flagStack[15]; //记录每个节点访问次数栈TreeNode *p = T;while(p!=NULL||top!=-1){if(p!=NULL){ //第一次访问,flag置1,入栈stack[++ top] = p;flagStack[top] = 1;p = p->lChild;}else{//(p == NULL)if(flagStack[top] == 1){ //第二次访问,flag置2,取栈顶元素但不出栈p = stack[top];flagStack[top] = 2;p = p->rChild;}else{ //第三次访问,出栈p = stack[top --];printf("%d\t",p->data); //出栈时,访问输出p = NULL; //p置空,以便继续退栈}}}}
007.重建二叉树

思路很简单,即是利用前序遍历寻找根节点,而后根据此根节点将中序遍历一分为二(代码写的很有意思)。
在寻找中序的位置时,最好适用hashmap来进行快速查找!
class Solution {int index = 0;public:TreeNode* rebuild(vector<int>& preorder, vector<int>& inorder, int left, int right) {if (index == preorder.size() || left == right)return NULL;TreeNode *head = NULL;for (int i = left; i<right; i++) {if (preorder[index] == inorder[i])//找到了分界点{head = new TreeNode(preorder[index]);index++;//前序遍历的index往后推移head->left = rebuild(preorder, inorder, left, i);//切分左子树head->right = rebuild(preorder, inorder, i+1, right);//切分右子树break;}}return head;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {TreeNode* head;int left = 0;int right = inorder.size();//起始条件head = rebuild(preorder, inorder, left, right);return head;}};
注:知道先序后序不能重构二叉树. 只有知道先序/后序中的其中一个和中序一起再能重构二叉树 假设有先序12435,后序42531 那么中序可以是42135,42153,24135,24153,42351,42531……等等!!
008.二叉树的下一个节点

分多种情况进行讨论:
① 如果一个节点有右子树不为空,那么该节点的下一个节点是右子树的最左节点;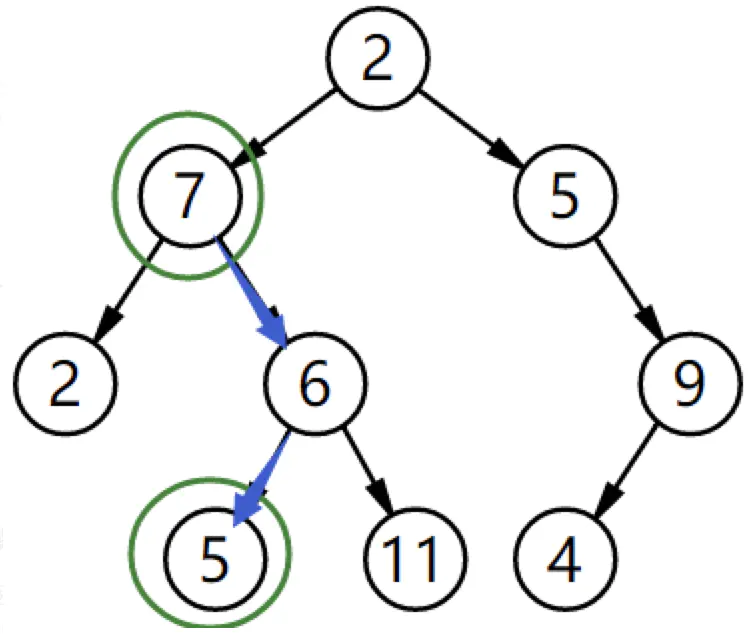
② 否则,向上找第一个左链接指向的树包含该节点的祖先节点。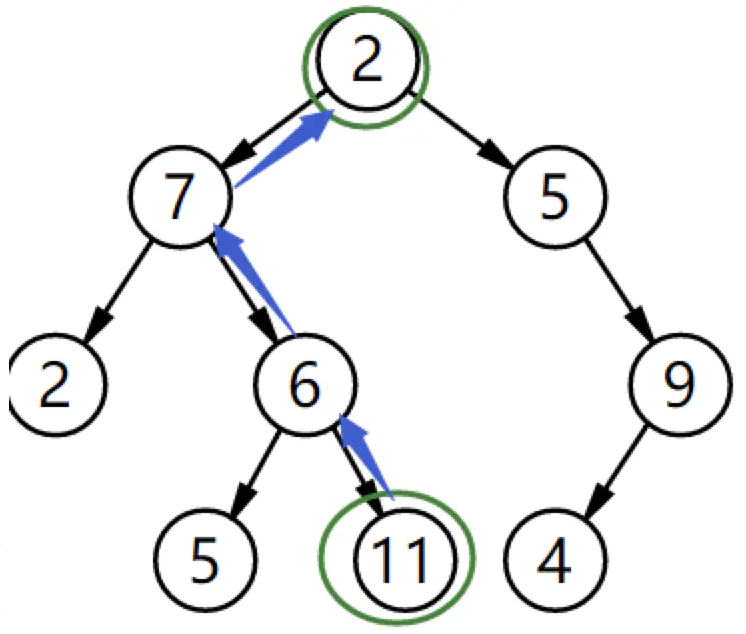
public class TreeLinkNode {int val;TreeLinkNode left = null;TreeLinkNode right = null;TreeLinkNode next = null;TreeLinkNode(int val) {this.val = val;}}public TreeLinkNode GetNext(TreeLinkNode pNode) {if (pNode.right != null) {TreeLinkNode node = pNode.right;while (node.left != null) node = node.left;return node;} else {while (pNode.next != null) {TreeLinkNode parent = pNode.next;if (parent.left == pNode) return parent;pNode = pNode.next;}}return null;}
009.用两个栈实现队列

实现思路,左手倒右手即可(即两个栈互为主从):(解题时可以利用画图来分析,便于理解其过程)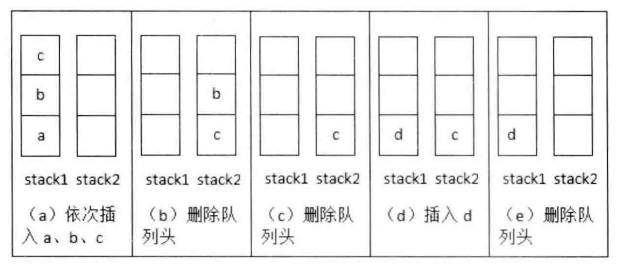
#include<stack>class CQueue {public:CQueue() {}void appendTail(int value) {Sin.push(value);}int deleteHead() {// 如果sou栈为空 那就把in栈压进去if (Sout.empty()) {while (!Sin.empty()) {Sout.push(Sin.top());Sin.pop();}}//不为空 那就弹出即可if (!Sout.empty()) {int res = Sout.top(); Sout.pop();return res;}else {return -1;}}private:stack<int> Sin, Sout;};

基本分析思路同上,用队列模拟一下栈的出入即可。
- 入栈:
将元素进队列A
- 出栈:
判断队列A中元素的个数是否为1,如果等于1,则出队列,
否则将队列A中的元素依次出队列并放入队列B,直到队列A中的元素留下一个,然后队列A最后一个元素出队列,再把队列B中的元素出队列依次放回队列A中。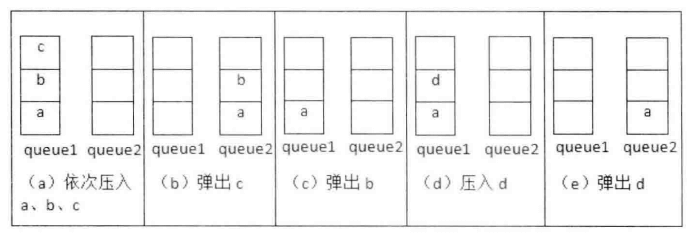
class MyStack {public:queue<int> que1;queue<int> que2;//辅助队列,用来备份/** Initialize your data structure here. */MyStack() {}/** Push element x onto stack. */void push(int x) {que1.push(x);}/** Removes the element on top of the stack and returns that element. */int pop() {int n=que1.size();n--;//为了留下最后一个元素while(n--)//将que1导入que2,但要留下最后一个元素{que2.push(que1.front());que1.pop();}int result=que1.front();//留下最后一个元素是要返回的值que1.pop();// woc 队列可以直接赋值?que1=que2;//再将que2赋值给que1,也可以以此出队并弹出while(!que2.empty())//清空que2{que2.pop();}return result;}/** Get the top element. */int top() {return que1.back();}/** Returns whether the stack is empty. */bool empty() {return que1.empty();}};
010.斐波拉契数列

递归虽然代码简洁,但是由于函数的调用和返回(参数的入栈和出栈)会造成性能损失,若递归次数过多,甚至可能引发栈溢出(其实主要问题还是由于子问题重叠,增加了许多不必要的计算次数),因此需要考虑循环、动态规划的方式;
几种方法:利用数组存放中间结果,需要空间消耗(即是所谓的备忘录法);
因为费布拉奇数列只和前两个有关,因此只利用两个变量来保留中间值,减小空间消耗;
动态规划:其实跟前两者一样,就是将之前的最优解保存下来(斐波拉契数列本质上不是一个标准的动态规划,因为动态规划涉及选择,而斐波拉契数列仅仅只是简单的螺旋上升)。
有一个公式(不实用): 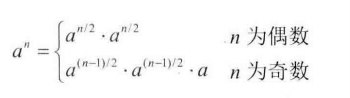
class Solution {public:int fib(int n) {if(n == 0) return 0;if(n == 1) return 1;int N = 0, NMinusOne = 1, NMinusTwo = 0;while(n >= 2){// 采取从下往上的方法,把计算过的中间项保存起来,避免重复计算导致递归调用栈溢出N = (NMinusOne + NMinusTwo) % 1000000007;NMinusTwo = NMinusOne;NMinusOne = N;n --;}return N;}};

其实跟上面一模一样:
class Solution {public:int numWays(int n) {vector<int>me={1,1,2};if(n<=2)return me[n];int minus1=2;int minus2=1;int result=0;for(int i=3;i<=n;i++){result=(minus1+minus2)%1000000007;minus2=minus1;minus1=result;}return result;}};

PS:考虑横着放和竖着放两种情况,如果竖着放,右边还剩2*7,那就是f(7);如果横着放(左边下面必须横着放一个),右边还剩2*6,那就是f(6)。所以最后的结果应该是f(8)=f(7)+f(6);
这道题其实跟上面两个都一样,就是斐波拉契数列的实际应用场景。
补充:哈希表的常用操作
unordered_map存储key-value的组合,unordered_map可以在常数时间内,根据key来取到value值。
find函数:iterator find ( const key_type& key )如果key存在,则find返回key对应的迭代器;如果key不存在,则find返回unordered_map::end。因此可以通过:map.find(key) == map.end()来判断,key是否存在于当前的unordered_map中。Count函数:size_type count ( const key_type& key ) constcount函数用以统计key值在unordered_map中出现的次数。实际上,c++ unordered_map不允许有重复的key。因此,如果key存在,则count返回1,如果不存在,则count返回0.//遍历输出+迭代器的使用auto iter = myMap.begin();//auto自动识别为迭代器类型unordered_map<int,string>::iteratorwhile (iter!= myMap.end()){cout << iter->first << "," << iter->second << endl; (这是一种常用的访问方式,在map中所有的值都是通过pair组合而成的)++iter;}myMap.insert(pair<int, string>(3, "陈二"));//使用insert和pair插入
补充:map和unordered_map的区别
map: map内部实现了一个红黑树(红黑树是非严格平衡二叉搜索树,而AVL是严格平衡二叉搜索树),红黑树具有自动排序的功能,因此map内部的所有元素都是有序的,红黑树的每一个节点都代表着map的一个元素。
map中的元素是按照二叉搜索树(又名二叉查找树、二叉排序树,特点就是左子树上所有节点的键值都小于根节点的键值,右子树所有节点的键值都大于根节点的键值)存储的,使用中序遍历可将键值按照从小到大遍历出来。
unordered_map: unordered_map内部实现了一个哈希表(也叫散列表,通过把关键码值映射到Hash表中一个位置来访问记录,查找的时间复杂度可达到O(1),其在海量数据处理中有着广泛应用)。因此,其元素的排列顺序是无序的。
Set:Set里面每个元素只存有一个key,它支持高效的关键字查询操作。set对应数学中的“集合”。
特点:
储存同一类型的数据元素(这点和**vector、queue等其他容器相同)
每个元素的值都唯一(没有重复的元素)
根据元素的值自动排列大小(有序性)(插入同样的值,不会改变原来的**set)
无法直接修改元素
高效的插入删除操作
(待补充,几种排序算法!必须会!!)
011.旋转数组的最小数字

如果直接遍历,时间复杂度是O(N),而且没有用上题目中所提供的全部条件:数组的旋转。根据大小的特性可以考虑使用二分法查找。
当考虑其中无重复元素(leetcode153)的时候:
class Solution {public:int findMin(vector<int>& nums) {int left = 0;int right = nums.size() - 1;while (left < right) {int mid = left + (right - left) / 2;///* 中值 > 右值,最小值在右半边,收缩左边界 */if (nums[mid] > nums[right]) {left = mid + 1;} else {right = mid;}}return nums[left];}};
当考虑到有重复的元素,其实只需要增加三行代码,进行下标的遍历(最坏情况下退化成数组遍历)
class Solution {public:int findMin(vector<int>& nums) {int left = 0, right = nums.size() - 1;while(left < right){int mid = left + (right - left) / 2;// 新加的三行代码,就是因为相等情况下无法判断具体区间,只能变化为不完全的二分查找if(nums[mid] == nums[right]){right--;continue;}if(nums[mid] > nums[right]) // 元素mid大于right,说明翻转点在mid之后(不包含mid)left = mid + 1;else // 元素mid小于right,说明翻转点在mid之前(包含mid)right = mid;}return nums[left];}};
012.矩阵中的路径

这道题可以遍历一遍格子(从中选择任何一个格子作为起点),看有没有某个格子能够成功找到路径,维护一个同矩阵同大小的标志矩阵;即是回溯法,可参考数据结构算法的回溯法章节(DFS很类似)
//刷剑指offer时一脸懵逼,回溯法学到了//为什么执行速度这么慢?class Solution {public:bool hasexit(vector<vector<char>>& board, string word, vector<vector<bool>>&haspassed, int row,int col,int index) {if (index == word.size())return true;if (row >= 0 && row < board.size() && col >= 0 && col < board[0].size() && haspassed[row][col]==false&&board[row][col] == word[index])//满足这些条件{haspassed[row][col] = true;if (hasexit(board, word, haspassed, row + 1, col, index + 1) ||//下hasexit(board, word, haspassed, row, col + 1, index + 1) ||//右hasexit(board, word, haspassed, row - 1, col, index + 1) ||//上hasexit(board, word, haspassed, row, col - 1, index + 1))//左{return true;}else {haspassed[row][col] = false;return false;}}return false;}bool exist(vector<vector<char>>& board, string word) {//1.排除一些特例if (board.empty() || word.empty())return false;//2.初始化参数int col = 0;int row = 0;int curindex = 0;int rows = board.size();int cols = board[0].size();vector<vector<bool>>haspassed(rows,vector<bool>(cols, false));//3.遍历所有的点for(row=0;row<rows;row++)for (col = 0; col < cols; col++) {if (hasexit(board, word, haspassed, row, col, curindex)) {return true;}}return false;}};
这个看起来简单一点:
class Solution {public:bool exist(vector<vector<char>>& board, string word) {if(word.empty()) return false;for(int i=0; i<board.size(); ++i){for(int j=0; j<board[0].size(); ++j){// 使用回溯法解题if(dfs(board, word, i, j, 0)) return true;}}return false;}bool dfs(vector<vector<char>>& board, string& word, int i, int j, int w){// 如果索引越界,或者值不匹配,返回falseif(i<0 || i>=board.size() || j<0 || j>=board[0].size() || board[i][j]!=word[w]) return false;if(w == word.length() - 1) return true;char temp = board[i][j];board[i][j] = '\0'; // 将当前元素标记为'\0',即一个不可能出现在word里的元素,表明当前元素不可再参与比较if(dfs(board,word,i-1,j,w+1)|| dfs(board,word,i+1,j,w+1)|| dfs(board,word,i,j-1,w+1)|| dfs(board,word,i,j+1,w+1)){// 当前元素的上下左右,如果有匹配到的,返回truereturn true;}board[i][j] = temp; // 将当前元素恢复回其本身值return false;}};
013.机器人的运动范围

基本的解法就是回溯法,类似于12题,只不过多了判断的条件。这道题通过大量的数据分析发现潜藏了一个优化方法,那就是只向右和下这两个方向进行搜索(这算是贪心算法吧);
class Solution {public:// 数位之和int digit_sum(int row, int col){int sum = 0;while (row){sum += row % 10;row /= 10;}while (col){sum += col % 10;col /= 10;}return sum;}// 返回能够到达的格子数int process(int m, int n, int k, int row, int col, vector<vector<bool>>& visited) {if (row < 0 || col < 0 || row >= m || col >= n){return 0;}if (digit_sum(row, col) > k){return 0;}if (visited.at(row).at(col)) //到达过{return 0;}int res = 1;visited.at(row).at(col) = true;res += process(m, n, k, row - 1, col, visited) + process(m, n, k, row + 1, col, visited) + process(m, n, k, row, col - 1, visited) + process(m, n, k, row, col + 1, visited);return res;}int movingCount(int m, int n, int k) {vector<vector<bool>> visited(m, vector<bool>(n));return process(m, n, k, 0, 0, visited);}};
补充:动态规划
014.**剪绳子** 
动态规划:O(n)的时间和空间消耗;
设f(i)为长度为i时,最大乘积,因此动态规划的公式就为:
f(k)=max(f(i)*f(k-i))
class Solution {public:int cuttingRope(int n) {if(n <= 3) return n - 1; // 当绳子的总长度<=3时,做特殊情况处理vector<int> res(n + 1, 0); // res[i]表示长度为i的绳子剪成若干段之后,乘积的最大值// 特殊处理:如果某个长度的绳子,剪了一下之后,其中一段的长度在[0,3]的区间内,就不要再剪这一段了// 因为剪了之后,乘积会变小,而res[i]是长度为i的绳子剪成若干段后能获得的最大乘积// 所以[res[0],res[3]]要单独处理(如下)res[0] = 0;res[1] = 1;res[2] = 2;res[3] = 3;int maxProduct = 0;for(int i=4; i<=n; ++i){maxProduct = 0;for(int j=1; j<=i/2; ++j){// 减少计算次数(因为比如1x3和3x1值是一样的,计算一次即可)int temp = res[j] * res[i-j];maxProduct = max(maxProduct, temp);res[i] = maxProduct;}}return res[n];}};
贪心算法:剪断的绳子有最优解;
当*_n>=5时,尽可能剪为3;**n为4时,剪为2_2;
//2.贪心算法,这是发现了一个规律//那就是在当n大于5的时候,剪为3或者2最好(两者比较之下3最好)//而当n为4的时候那就剪成2*2class Solution {public:int cuttingRope(int n) {vector<int>result={0,0,1,2};if(n<4)return result[n];//自下而上进行最优解的选定int cut3=n/3;if((n-3*cut3)==1)//即在最后一刀的地方暂停{cut3--;}int cut2=(n-3*cut3)/2;return pow(3,cut3)*pow(2,cut2);}};
015.**二进制中1的个数**

利用循环移位或者%取余来进行移动;
//有可能是负数,循环移动时需要补1//正数和负数的移动方向不一样class Solution {public:int hammingWeight(uint32_t n) {if (n == 0)return 0;//因为向右取1如果是负数就会多1if (n<0)n=~n;int countOne = 0;for (int i = 0; i<32; i++) {if (n % 2 == 1)//奇数,即末尾为1countOne++;n=n >> 1;}return countOne;}};


int hammingWeight(uint32_t n) {
int count = 0;
while(n)
{
n = n & (n-1);
++count;
}
return count;
}
补充:广度优先算法与深度优先算法(**BFS与DFS)**
针对图和树的遍历算法。DFS和BFS的实现细节在于,DFS**是利用栈(后进先出,朝某一个方向走到头,而后返回,有时是利用递归实现的(因为函数递归其实也是栈));BFS是利用队列(先进先出,一层一层的将当前节点放入队列而后出队列);
广度优先搜索的缺点:在树的层次较深&子节点数较多的情况下,消耗内存十分严重。广度优先搜索适用于节点的子节点数量不多,并且树的层次不会太深的情况。
那么深度优先就可以克服这个缺点,因为每次搜的过程,每一层只需维护一个节点。但回过头想想,广度优先能够找到最短路径,那深度优先能否找到呢?深度优先的方法是一条路走到黑,那显然无法知道这条路是不是最短的,所以你还得继续走别的路去判断是否是最短路?
深度优先搜索的缺点:难以寻找最优解,仅仅只能寻找有解。其优点就是内存消耗小,克服了刚刚说的广度优先搜索的缺点。**
016.**数值的整数次方**

难点就在于底和幂如果小于**1(0或者负数)会怎样呢?
也就是说在计算的时候需要多判断一下,另外似乎这个运算是不计较分数次幂的,因为幂是int型。(这道题的难点是考虑全面)
而且还要考虑异常,比如对0求倒数,需要一个全局变量/异常/返回值来提示用户。
PS:另外,在求某树的几次方时,例如100次方,我们并不需要真的算99次乘法,而是只需要50次,即50*50;这就是快速幂算法。
递归的解法:
double myPow(double x, int n) {
if(n==0)
return 1;
if(n==1)
return x;
if(n==-1)
return 1/x;
double half=myPow(x,n/2);
double res=myPow(x,n%2);
return halfreshalf;
}
迭代的解法:思想是奇数多乘一次x,偶数直接x乘方*;
double myPow(double x, int n) {
if(n<0)
return 1/myPow(x,-n);
double re = 1;
for (int i = n; i > 0; i /= 2) {
if(i%2 != 0) { //如果i是奇数(对应的二进制位为1,贡献到结果里)
re = x;//对应的结果就产生权重
}
x *= x;//依次迭代
}
return re;
}
017.*打印从1到最大的n位数(*)

这种题一定得思考大数问题,而一旦涉及大数问题基本就是用字符串来表示数字。(这种数字打印的题必考)。
主体代码如下:
难点就在于如何判断有没有进位,以及如何按照日常阅读习惯打印出最后的数据(遇到第一个非**0的字符才开始打印)。
也就是分为三个部分,主函数,字符串相加函数,省0操作(直到找到第一个非0的数字)。
class Solution {
public:
vector
//主函数
vector
// 以下注释的前提:假设 n = 3
if(n <= 0) return vector
string s(n, ‘0’); // s最大会等于999,即s的长度为n
while(!overflow(s)) inputNumbers(s);
return output;
}
//数字相加的操作
bool overflow(string& s)
{
// 本函数用于模拟数字的累加过程,并判断是否越界(即 999 + 1 = 1000,就是越界情况)
bool isOverFlow = false;
int carry = 0; // carry表示进位
// 从后往前计算
for(int i=s.length()-1; i>=0; —i)
{
int current = s[i] - ‘0’ + carry; // current表示当前这次的操作
if(i == s.length() - 1) current ++; // 如果i此时在个位,current执行 +1 操作
if(current >= 10)
{
// 假如i已经在最大的那一位了,而current++之后>=10,说明循环到头了,即999 + 1 = 1000
if(i == 0) isOverFlow = true;
else
{
// 只是普通进位,比如current从9变成10
carry = 1;
s[i] = current - 10 + ‘0’;
}
}
else
{
// 如果没有进位,更新s[i]的值,然后直接跳出循环,这样就可以回去执行inputNumbers函数了,即往output里添加元素
s[i] = current + ‘0’;
break;
}
}
// 越界的就不用管了哈
return isOverFlow;
}
void inputNumbers(string s)
{
// 本函数用于循环往output中添加符合传统阅读习惯的元素。比如001,我们会1而不是001。
bool isUnwantedZero = true; // 判断是否是不需要添加的0,比如001前面的两个0
string temp = “”;
for(int i=0; i
if(isUnwantedZero && s[i] != ‘0’) isUnwantedZero = false;
if(!isUnwantedZero) temp += s[i];
}
output.push_back(stoi(temp));
}
};
还有一种解法,从排列来考虑:打印到n位的数据其实就是n个0到9的全排列,
class Solution
{
public:
vector
{
vector
if (n < 0)
{
return nums;
}
string num(n, ‘0’);
Recurse(nums, num, n, 0);
return nums;
}
/*递归实现从最高位到最低位的数字全排列*/<br /> void Recurse(vector<int>& nums, string& num, int n, int index)<br /> {<br /> if (index == n) //如果索引index指向最低位的右侧,则到达递归边界,保存当前数字后返回<br /> {<br /> Save(nums, num);<br /> return;<br /> }<br /> else<br /> {<br /> for (int i = 0; i <= 9; i++) //每一位数从0到9排列,记录当前位数的一种情况后递归进行下一位数的排列<br /> {<br /> num[index] = '0' + i;<br /> Recurse(nums, num, n, index + 1);<br /> }<br /> }<br /> }/*实现字符串数字去掉高位0并转换为int存入nums向量操作*/<br /> void Save(vector<int>& nums, string num)<br /> {<br /> string temp_s = "";<br /> bool IsBeginZero = true; //高位0标记<br /> //找到第一个非0的有效数字<br /> for (int i = 0; i < num.size(); i++)<br /> {<br /> if (IsBeginZero && num[i] != '0')<br /> {<br /> IsBeginZero = false;<br /> }<br /> if (!IsBeginZero)<br /> {<br /> temp_s += num[i];<br /> }<br /> }<br /> if (temp_s != "") //注意全排列递归解法在排列时会产生全0如"00000",导致temp_s为空,此时不能转换为整数<br /> {<br /> int temp_i = stoi(temp_s);<br /> nums.push_back(temp_i);<br /> }<br /> }<br />};
018.**删除链表的节点**

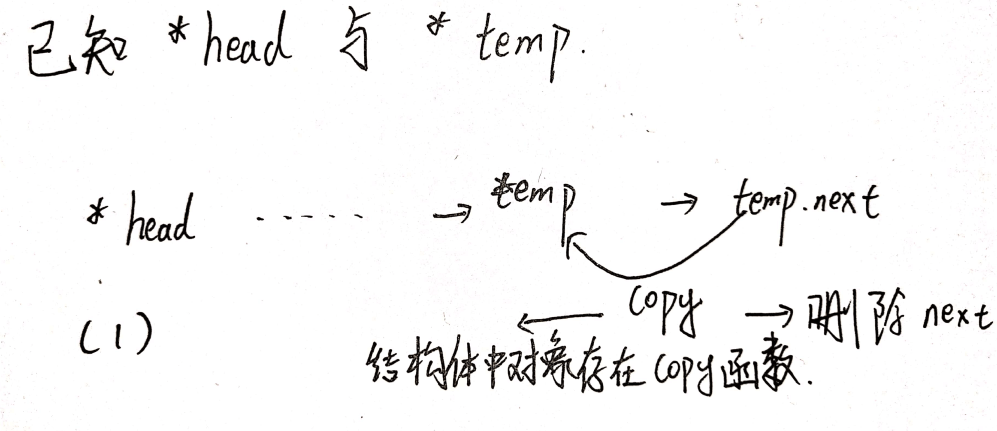
也就是用next节点的下一个节点的信息覆盖next,而后删除next的下一个节点,那么就相当于删掉了**next原节点*。
ListNode DeleteNode(ListNode head, ListNode pToBeDeleted){
if(!head || !pToBeDeleted){
return nullptr;
}
// 要删除的节点不是尾节点
if(pToBeDeleted->next != nullptr){
ListNode *pNext = pToBeDeleted->next;
pToBeDeleted->val = pNext->val;
pToBeDeleted->next = pNext->next;
delete pNext;<br /> pNext = nullptr;<br /> }<br /> // 链表只有一个节点,删除头结点<br /> else if(head == pToBeDeleted){<br /> delete pToBeDeleted;<br /> pToBeDeleted = nullptr;<br /> head = nullptr; <br /> }<br /> // 链表中有多个节点,删除尾节点<br /> else{<br /> ListNode *h = head;<br /> while(h->next != pToBeDeleted){<br /> h = h->next;<br /> }<br /> h->next = nullptr;<br /> delete pToBeDeleted;<br /> pToBeDeleted = nullptr; <br /> }<br /> return head;<br />}<br />Leetcode改编之后,**只能够用遍历的方式**,找到了就进行修改:<br />ListNode* deleteNode(ListNode* head, int val) {<br /> if(head->val == val) return head->next;<br /> ListNode *pre = head, *cur = head->next;<br /> while(cur != nullptr && cur->val != val) {<br /> pre = cur;<br /> cur = cur->next;<br /> }<br /> if(cur != nullptr) pre->next = cur->next;<br /> return head;<br /> }<br /><br /><br />ListNode* removeDuplicateNodes(ListNode* head) {<br /> if (head == nullptr)<br /> return head;ListNode* cur = head;while (cur)<br /> {<br /> ListNode* prev = cur;<br /> while (prev->next) //遍历到链表尾,删除值等于cur->val的所有节点<br /> {<br /> if (prev->next->val == cur->val)<br /> {<br /> prev->next = prev->next->next;<br /> }<br /> else<br /> {<br /> prev = prev->next;<br /> }<br /> }cur = cur->next;<br /> }return head;<br /> }<br />};<br />还可以使用hash表:<br />class Solution {<br />public:<br /> ListNode* removeDuplicateNodes(ListNode* head) {<br /> if (head == nullptr)<br /> {<br /> return nullptr;<br /> }<br /> unordered_map<int,int> existed;<br /> // 第一节点肯定保留<br /> ListNode* curr = head;<br /> existed[curr->val] = 1;<br /> // 优化点:这里用 curr->next 去遍历,这样子可以省去后续忽略结点的 next->next的额外判断<br /> while (curr->next != nullptr)<br /> {<br /> int val = curr->next->val;<br /> // 存在则直接忽略<br /> if (!existed[val]) <br /> {<br /> existed[val] = 1;<br /> curr = curr->next;<br /> }<br /> else<br /> {<br /> curr->next = curr->next->next;<br /> }<br /> }<br /> return head;<br /> }<br />};
019.正则表达式匹配

正则表达式是一种非常重要的题型。详细分析一下:
如果模式中的字符ch是‘.’,可匹配任何一个字符;
如果模式中的字符ch不是‘.’,且字符串里是ch,也匹配;
如果模式中的字符是‘’,需要分成以下的情况讨论:(其实是一种状态机)(这道题的难点就在于对号的理解,没什么难的)
如果下一位有号,那么会有三种情况:
恰好匹配,号就当不存在;
不匹配,无视号及其前的字符;
匹配,字符串往前移动一位。
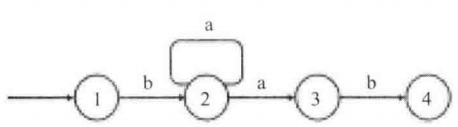
动态规划解法:
本题的状态共有 m ×n 种,应定义状态矩阵 dp ,dpi代表 s[:i]与 p[:j]是否可以匹配。 
/思路
dp[i][j] 表示 s 的前 i个是否能被 p 的前 j 个匹配
关键点在于p的下一个字符是否为
如果为,那么可以匹配0次(和前字母跳过)一次(跳过)或者多次(等待)
/
class Solution {
public:
bool isMatch(string s, string p) {
//边界值
if(p.empty()){
return s.empty();
}
//为什么是size+1呢?因为是从0(空字符)开始的啊,所以实际长度要加1
//上面说的0不是下标0啊
int m = s.size() + 1, n = p.size() + 1;
vector
dp[0][0] = true;
// 初始化首行(如果s为空,p不为空,当且仅当p有连续跳)
for(int j = 2; j < n; j += 2)
{
if(p[j-1]==’‘&&dp[0][j-2]){
dp[0][j]=dp[0][j-2];
}
}
// 状态转移
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
//先处理不为‘’
if(p[j-1]!=’‘){
//字符匹配
dp[i][j]=(dp[i-1][j-1]&&s[i-1]==p[j-1])||(dp[i-1][j-1]&&p[j-1]==’.’);
}
else {
//三种情况
//1.不需要,那就直接跳过,跟j-2匹配
//2.匹配,那只跟i-1匹配
//3.匹配,且用到.
dp[i][j]=(dp[i][j-2])||(dp[i-1][j]&&s[i-1]==p[j-2])||(dp[i-1][j]&&p[j-2]==’.’);
}
}
}
return dp[m - 1][n - 1];//因为有m+1的长度
}
};
或者用指针的方法: 
class Solution {
public:
bool isMatch(string s, string p) {
return match(s.data(), p.data());
}
bool match(char s, char p) {
if (!p) return !s;
if ((p + 1) != ‘‘)
return s == p || (p == ‘.’ && s != ‘\0’) ? match(s + 1, p + 1) : false;
else
return s == p || (p == ‘.’ && s != ‘\0’) ? match(s, p + 2) || match(s + 1, p) : match(s, p + 2);
//或者return (s == p || (p == ‘.’ && *s != ‘\0’)) && match(s + 1, p) || match(s, p + 2);
}
};
020.表示数值的字符串

这道题跟019类似,都是属于“模板匹配”类题型,只不过约束条件不一样。关键就在于分析清楚到底有哪些可能的出现形式以及逻辑判断,在面试的时候跟面试官讨论。
class Solution {
public:
bool isNumber(string s) {
int n = s.size();
int index = -1;
bool hasDot = false,hasE = false,hasOp = false,hasNum = false;
//去除空格
while(index
if(‘0’<=s[index] && s[index]<=’9’){
hasNum = true;
//找到了e
}else if(s[index]==’e’ || s[index]==’E’){
if(hasE || !hasNum) return false;
hasE = true;
hasOp = false;hasDot = false;hasNum = false;
//看看是否有正负号
}else if(s[index]==’+’ || s[index]==’-‘){
if(hasOp || hasNum || hasDot) return false;
hasOp = true;
//找到了小数点
}else if(s[index]==’.’){
if(hasDot || hasE) return false;
hasDot = true;
}else if(s[index]==’ ‘){
break;
}else{
return false;
}
++index;
}
while(index
}
};
021.使奇数位于偶数前面(参考第二种题解)

交换顺序的题,很大可能是用双指针。即利用双指针的方法进行奇数偶数的快速交换(如果需要保持数组的相对关系,那么应该从末尾往前进行双指针遍历)
高阶版本,考虑可扩展性,这里所说的可扩展性是指“奇数位于偶数前面”这一限制条件可以更改成任意的数学关系。即将此题解法拓展为可复用修改的代码。
PS:剑指offer官方题解中使用了函数指针,值得学习。
class Solution {
public:
vector
if(nums.size()==0)
return nums;
auto p1 = 0;
auto p2 = nums.size()-1;
while (p1
while (p1
if (p1
nums[p1] = nums[p2];
nums[p2] = temp;
}
}
return nums;
}
};
022.链表中倒数第k个节点

最简单的方法,将链表节点依次压入栈,而后弹出想要的节点即可。
进阶一点呢,快慢指针,快指针先走k步,而后慢指针快指针同时前进,当快指针到达的时候,慢指针所指即是所需的节点。(但是关于快慢指针一定得注意是否会越界或者出现其他的错误信息)
ListNode getKthFromEnd(ListNode head, int k) {
if(head==NULL||k==0)//第一/二种情况
return NULL;
ListNode before=head;
ListNode behind=head;
for(int i=0;i<k-1;i++){<br /> before=before->next;<br /> if(before==NULL)<br /> return NULL;<br /> }while(before->next!=NULL){<br /> before=before->next;<br /> behind=behind->next;<br /> }<br /> return behind;}
023.链表中环的入口节点

利用快慢指针:先找到快慢指针相遇的那个点。
先找到相遇点,然后快指针重置为慢指针,同时走,再次相遇即是入口点;或是先看环有多少个点,而后让一个指针先走这么多点,重合处即是入口节点。(算法手册有相同的题解)
ListNode detectCycle(ListNode head) {
if(head==nullptr)
return head;
ListNode slow=head;
ListNode fast=head;
//找相遇点
while(fast!=nullptr&&fast->next!=nullptr){
fast=fast->next;
fast=fast->next;
slow=slow->next;
if(fast==slow)
break;
}
//确认是否有环
if(fast==nullptr||fast->next==nullptr){
return nullptr;
}
//找入口节点
fast=head;
while(fast!=slow){
fast=fast->next;
slow=slow->next;
}
return fast;
}
024.反转链表

这道题可参考算法手册6.6。
简单来说可以用三个变量存储前中后三个指针,重新调整其映射关系。亦或是用栈,亦或是递归。
class Solution {private:ListNode* curNode;ListNode* nextNode;ListNode* preNode;public:ListNode* reverseList(ListNode* head) {if(NULL==head)return NULL;curNode=head;preNode=NULL;//保存前while(curNode!=NULL){nextNode=curNode->next;if(nextNode==NULL){curNode->next=preNode;break;}curNode->next=preNode;preNode=curNode;curNode=nextNode;}return curNode;}};
递归如下:
ListNode reverse(ListNode head){if (head.next == null) return head;ListNode last = reverse(head.next);head.next.next = head;head.next = null;return last;}
单独看代码有些让人难以理解,先解释一下这个函数的定义:输入一个节点head,将「以head为起点」的链表反转,并返回反转之后的头结点。
其中最重要的两步是:head.next.next=head;
head.next=null;
025.合并两个排序的链表

两个要点:合并顺序以及特殊情况,如空链表。
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {if(!l1) return l2;if(!l2) return l1;//这是递归的方法if(l1 -> val < l2 -> val){l1 -> next = mergeTwoLists(l1 -> next, l2);return l1;}else{l2 -> next = mergeTwoLists(l1, l2 -> next);return l2;}}
迭代的方法
class Solution {public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {//太妙了!!ListNode* dummy = new ListNode(0), *pre = dummy;while (l1 && l2) {if (l1->val < l2->val) {pre->next = l1;pre = pre->next;l1 = l1->next;} else {pre->next = l2;pre = pre->next;l2 = l2->next;}}if (l1) pre->next = l1;if (l2) pre->next = l2;return dummy->next;}};
026.树的子结构

将B用前序遍历或是后序遍历的方式进行表征,再对A的每个节点进行递归表征,如果有相同的,那就是同一结构(其实还不如下面的解法简单)。
或是直接对每一个节点进行遍历比较(A/B)。先找到根节点相同的子树,而后对两者的左右子树进行比较。
递归的方法,复杂度较高
class Solution {public:bool isSubStructure(TreeNode* A, TreeNode* B) {if(A == NULL || B == NULL) return false;if(A->val == B->val && scan(A,B)) return true; //是否存在满足条件的子结构,按根左右遍历return isSubStructure(A->left,B) || isSubStructure(A->right,B);}bool scan(TreeNode* A, TreeNode* B) {if(B == NULL) return true;if(A == NULL) return false;if(A->val != B->val) return false;return scan(A->left,B->left) && scan(A->right, B->right);}};
027.二叉树的镜像

递归,每一个子树就交换其左右即可。
BTNode* Mirror(BTNode* root){if(root==nullptr)return root;if(root->left==nullptr&&root->right==nullptr)return root;BTNode* temp =root->left;root->left=root->right;root->right=temp;if(root->left)Mirror(root->left);if(root->right)Mirror(root->right);return root;}
或是利用辅助栈
class Solution {public:TreeNode* mirrorTree(TreeNode* root) {if(root == nullptr) return nullptr;stack<TreeNode*> stack;stack.push(root);// 将所有的节点都压入栈while (!stack.empty()){TreeNode* node = stack.top();stack.pop();if (node->left != nullptr) stack.push(node->left);if (node->right != nullptr) stack.push(node->right);// 交换左右节点TreeNode* tmp = node->left;node->left = node->right;node->right = tmp;}return root;}};
028.对称的二叉树

利用遍历的方法:定义一个跟前序遍历相反的遍历方式:先根节点,再右节点再左节点,如果前序遍历的结果和新型遍历的结果相等,那么就是对称的(需要把空节点null放进去);
//这里是用数字来作为存储方式,-1代表null,但是保险起见可以使用字符串来保存(虽然开销比较大)vector<int> res1;vector<int> res2;//前序遍历方式void front(TreeNode* node){if(node==NULL){res1.push_back(-1);return;}res1.push_back(node->val);front(node->left);front(node->right);return;}//反向前序遍历方式void mirrorfront(TreeNode* node){if(node==NULL){res2.push_back(-1);return;}res2.push_back(node->val);mirrorfront(node->right);mirrorfront(node->left);return;}bool isSymmetric(TreeNode* root) {front(root);mirrorfront(root);if(res1==res2)return true;return false;}
还有另外一种迭代的方式,那就是使用类似于层序遍历的思想:
class Solution {public:bool isSymmetric(TreeNode* root) {if (root == NULL) return true;queue<TreeNode*> que;que.push(root->left); // 将左子树头结点加入队列que.push(root->right); // 将右子树头结点加入队列while (!que.empty()) { // 接下来就要判断这这两个树是否相互翻转TreeNode* leftNode = que.front(); que.pop();TreeNode* rightNode = que.front(); que.pop();if (!leftNode && !rightNode) { // 左节点为空、右节点为空,此时说明是对称的continue;}// 左右一个节点不为空,或者都不为空但数值不相同,返回falseif ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {return false;}//其实这个地方也可以将这一层的节点给存入一个string中,只需要判断这个string是不是一个回文字符串即可!!que.push(leftNode->left); // 加入左节点左孩子que.push(rightNode->right); // 加入右节点右孩子que.push(leftNode->right); // 加入左节点右孩子que.push(rightNode->left); // 加入右节点左孩子}return true;}};
利用递归的方式:这个递归的函数不要跳进去,而是画图来分析何为镜像。
//对于每个节点来说,如何判断是否为对称的呢?//左节点的右子节点,对应,右节点的左子节点;bool isSymmetric(TreeNode* root) {if(root==null)return true;return JudgeIs(root->left,root->right);}bool JudgeIs(TreeNode* l,TreeNode* r){if(!l&&!r)//左右节点都为空return true;if(!l||!r)//左右只有一个return flase;if(l->val!=r->val)return false;return JudgeIs(l->left,r->right)&&JudgeIs(l->right,r->lrft);}
029.顺时针打印矩阵

简单的方法控制行和列的全局变量,按照右-》下-》左-》上-》右的方式打印,打印一次就缩小范围(修改全局变量);
还有其他的解法吗?并没有。(以下方法最简洁)
//先实现输出最外面一圈vector<int> spiralOrder(vector<vector<int>>& matrix) {if (matrix.size() == 0)return{};int L = 0;int R = matrix[0].size() - 1;int U = 0;int D = matrix.size() - 1;vector<int> res;while (L <= R&&U <= D) {//向右平移for (int i = L; i <= R; i++) {res.push_back(matrix[U][i]);}U++;if(res.size()==matrix[0].size()*matrix.size())break;//向下for (int i = U; i <= D; i++) {res.push_back(matrix[i][R]);}R--;if(res.size()==matrix[0].size()*matrix.size())break;//向左for (int i = R; i >= L; i--) {res.push_back(matrix[D][i]);}D--;if(res.size()==matrix[0].size()*matrix.size())break;//向上for (int i = D; i >= U; i--) {res.push_back(matrix[i][L]);}L++;if(res.size()==matrix[0].size()*matrix.size())break;}return res;
030.包含min函数的栈

题目很简单,就是这个栈能够输出最小值,难点在于如果最小值被pop之后,如何保存第二小的值。
解决方式很简单,设置一个辅助栈,用来保存当当前最小值被推出之后的新最小值。
注意,这个最小值栈里存的是可能成为最小值的元素,其他的元素休想进去!
class MinStack {private:stack<int> minValue;stack<int> minStack;public:/** initialize your data structure here. */MinStack() {;}void push(int x) {if(minValue.empty()||x<=minValue.top())minValue.push(x);minStack.push(x);}void pop() {//这个是重点!if(minStack.top()==minValue.top())minValue.pop();minStack.pop();}int top() {return minStack.top();}int min() {return minValue.top();}};
031.栈的压入、弹出序列

解决这道题需要深刻理解栈的压入和弹出的顺序。
其实很好理解:
第一步:从压栈序列一直往里压入,直到等于弹出序列的第一个元素。
第二步:弹出该函数,弹出后看栈顶是否等于弹出序列的第二个,如果不等那就继续压,如果没有可压入的元素之后。栈顶依旧不等,那就说明不是弹出序列。
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {stack<int> st;int n = popped.size();int j = 0;for (int i = 0; i < pushed.size(); ++i){st.push(pushed[i]);while(!st.empty() && j < n && st.top() == popped[j]){st.pop();++j;}}return st.empty();}
032.从上到下打印二叉树

关键点就是如何实现一层一层的打印节点,用队列,压入根结点而后逐个弹出打印再压入子节点。
vector<int> levelOrder(TreeNode* root) {//先看是否为空树if(root == nullptr)return {};vector<int> ans;queue<TreeNode*> Bfs;//将根节点加入队列Bfs.push(root);while(!Bfs.empty()){TreeNode* temp = Bfs.front();//开始广度优先搜索ans.push_back(Bfs.front()->val);Bfs.pop();if(temp->left)Bfs.push(temp->left);if(temp->right)Bfs.push(temp->right);}return ans;}
PS:那么如何遍历一幅有向图呢?也用队列来实现,其实树是图的一种退化形式(图可以有很多节点,而树只能有两个)从上到下遍历二叉树,其实就是广度遍历二叉树。<br /> 那如果是按层的顺序,**分行打印节点又该如何呢**?<br /><br /> **关键就在于如何确定一层的终止:****增加一个变量**用来记录当前**层需要打印的节点数目**。同时在**压入下一层节点的时候增加一个下一层节点数目的变量**。整体框架完全是基于二叉树的打印来的。
vector<vector<int>> levelOrder(TreeNode* root) {//先看是否为空树if(root == nullptr)return {};vector<int> tempans;vector<vector<int>> res;queue<TreeNode*> Bfs;int curNodes=0;int nextNodes=0;//将根节点加入队列Bfs.push(root);curNodes++;while(!Bfs.empty()){TreeNode* temp = Bfs.front();//开始广度优先搜索tempans.push_back(Bfs.front()->val);Bfs.pop();if(temp->left){Bfs.push(temp->left);nextNodes++;}if(temp->right){Bfs.push(temp->right);nextNodes++;}if(--curNodes<1){res.push_back(tempans);tempans.clear();curNodes=nextNodes;nextNodes=0;}}return res;}
再变一变,**如果是按之字形(或其他形式)打印二叉树呢?**<br />方法一是利用双端队列,**且存取的顺序需要进行变动**。直接看解答:
vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> res;if (root==NULL)return res;bool flag = true; //从左向右打印为true,从右向左打印为falsedeque<TreeNode*> q;q.push_back(root);while (!q.empty()){int n = q.size();vector<int> out;TreeNode* node;while (n>0){if (flag) // 前取后放:从左向右打印,所以从前边取,后边放入{node = q.front();q.pop_front();if (node->left)q.push_back(node->left); // 下一层顺序存放至尾if (node->right)q.push_back(node->right);}else //后取前放: 从右向左,从后边取,前边放入{node = q.back();q.pop_back();if (node->right)q.push_front(node->right); // 下一层逆序存放至首if (node->left)q.push_front(node->left);}out.push_back(node->val);n--;}flag = !flag;res.push_back(out);}return res;}
或是利用reverse的方式进行,即将顺序放到最后才来打乱:
class Solution {
public:
vector
vector
search(ans, root, 0);
for(int i = 1; i < ans.size(); i+=2)
reverse(ans[i].begin(), ans[i].end());
return ans;
}
void search(vector<vector<int>> &ans, TreeNode* root, int depth){<br /> if(root == NULL)<br /> return;<br /> if(depth >= ans.size())<br /> ans.push_back(vector<int>());<br /> ans[depth].push_back(root->val);<br /> search(ans, root->left, depth+1);<br /> search(ans, root->right, depth+1);<br /> return;<br /> }<br />};<br />要想实现上下两层不同方向的打印,**可以画图来具体分析:需要使用栈来实现,而且是两个栈。同时,保存在栈的左右子节点的顺序也是有要求的**。
vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> res;if (root == nullptr) return res;stack<TreeNode *> stk1;stk1.push(root);stack<TreeNode *> stk2;while (!stk1.empty() || !stk2.empty()) {if (!stk1.empty()) {res.push_back(vector<int>());while (!stk1.empty()) {TreeNode *cur = stk1.top();stk1.pop();res.back().push_back(cur->val);if (cur->left != nullptr) stk2.push(cur->left);if (cur->right != nullptr) stk2.push(cur->right);}}if (!stk2.empty()) {res.push_back(vector<int>());while (!stk2.empty()) {TreeNode *cur = stk2.top();stk2.pop();res.back().push_back(cur->val);if (cur->right != nullptr) stk1.push(cur->right);if (cur->left != nullptr) stk1.push(cur->left);}}}return res;}
**PS****:我才知道可以这么声明栈!stack<TreeNode*> nodestack[2];(即是同时声明两个!)**
033.二叉搜索树的后序遍历序列


审题:二叉搜索树?后序遍历?有什么性质?
中序遍历倒是从小到大,那么后序遍历···只能从根节点大于左小于右来看了:
比如 5 7 6 9 11 10 8
8肯定是根节点;
第一个数5<8,说明存在左子树5 7 6,右子树 9 11 10(即以8来切分);
对于5 7 6,有分为左右;9 11 10 又分···
class Solution {private:bool DFS(int Start, int End, vector<int>& postorder) {if(Start >= End) return true;int Standard = postorder[End]; //最后一个为根节点,前半段小于根,后半段大于根int Break = Start; //找到小于根和大于根的分界点while(postorder[Break] < Standard) Break++;for(int i = Break; i < End; i++) {if(postorder[i] <= Standard) return false;}return DFS(Start, Break-1, postorder) && DFS(Break, End - 1, postorder);}public:bool verifyPostorder(vector<int>& postorder) {if(postorder.size() < 2) return true;return DFS(0, postorder.size() - 1, postorder);}};
034.二叉树中和为某一值的路径

利用回溯法,结合前序遍历:本节点-》左节点-》右节点
ector<vector<int>> pathSum(TreeNode* root, int sum) {vector<vector<int>> res;vector<int> cur;dfs(root, sum, res, cur);return res;}void dfs(TreeNode* root, int sum, vector<vector<int>>& res, vector<int>& cur){if(root == NULL) return ;cur.push_back(root->val);sum -= root->val;if(sum == 0 && !(root->left) && !(root->right)) res.push_back(cur); //满足路径条件dfs(root->left, sum, res, cur);dfs(root->right, sum, res, cur);cur.pop_back(); //关键点:回溯}
035.复杂链表的复制


这种复杂链表的难点就在于如何让m_pSibling指向正确的链表节点:
哈希表?在创建新节点时,构建与旧节点的映射关系。
于是整个构造过程分为两步:
第一步,复制新链表(这时m_Sibling指向旧节点中的节点),同时建立新旧节点间的映射关系;
第二步,遍历新链表,利用hash表映射;
Node* copyRandomList(Node* head) {if(head == nullptr) return nullptr;Node* cur = head;unordered_map<Node*, Node*> map;// 3. 复制各节点,并建立 “原节点 -> 新节点” 的 Map 映射while(cur != nullptr) {map[cur] = new Node(cur->val);cur = cur->next;}cur = head;// 4. 构建新链表的 next 和 random 指向while(cur != nullptr) {map[cur]->next = map[cur->next];map[cur]->random = map[cur->random];cur = cur->next;}// 5. 返回新链表的头节点return map[head];}
另一种方法是不使用辅助空间,而是类似于一种几何里作辅助线的方式:(新建的节点位于旧节点的后面,而后只需要做一个分离操作即可)
Node* copyRandomList(Node* head) {if(head == nullptr) return nullptr;Node* cur = head;// 1. 复制各节点,并构建拼接链表while(cur != nullptr) {Node* tmp = new Node(cur->val);tmp->next = cur->next;cur->next = tmp;cur = tmp->next;}// 2. 构建各新节点的 random 指向cur = head;while(cur != nullptr) {if(cur->random != nullptr)cur->next->random = cur->random->next;cur = cur->next->next;}// 3. 拆分两链表Node* pre = head, *res = head->next;cur = head->next;while(cur->next != nullptr) {pre->next = pre->next->next;cur->next = cur->next->next;pre = pre->next;cur = cur->next;}pre->next = nullptr; // 单独处理原链表尾节点(null)return res; // 返回新链表头节点}
036.二叉搜索树和双向链表

递归!递归!
思路:中序遍历的同时构造双向链表。
class Solution {public:Node* pre, *head;Node* treeToDoublyList(Node* root) {if (!root) return NULL;inorder(root);head->left = pre; //中序遍历完成后,pre指针会指向第一个最小的节点pre->right = head;return head;}// 理解递归!!void inorder(Node* root){if (!root) return;inorder(root->left);if (!pre) head = root; //中序遍历第一个节点最小,此时pre为空else pre->right = root; //前一个节点的右边指向当前节点root->left = pre; //当前节点的左边指向前一个节点构成双向链表pre = root; //最后让pre指针指向当前节点,开始下一轮dfsinorder(root->right);}};
迭代的方式需要先保存:
Node* treeToDoublyList(Node* root) {if(!root) return NULL;vector<Node*> inorderindex;inorder(inorderindex,root);for(int i = 0;i < inorderindex.size()-1;i++){inorderindex[i]->right = inorderindex[i+1];}for(int j = inorderindex.size()-1;j>=1;j--){inorderindex[j]->left = inorderindex[j-1];}// 这是题目的要求,成环inorderindex[inorder1.size()-1]->right = inorderindex[0];inorderindex[0]->left = inorderindex[inorderindex.size()-1];Node* head = inorder1[0];return head;}void inorder(vector<Node*> &inorderindex,Node* root){if(root == NULL) return ;inorder(inorderindex,root->left);inorderindex.push_back(root);inorder(inorderindex,root->right);}
037.序列化二叉树(重点)

算法手册中讲过原理:7.6
class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode root) {
if(!root){
return “”; // 判空
}
ostringstream out;
queue<TreeNode> bfs;
bfs.push(root);
while(!bfs.empty()){
// 迭代法
TreeNode temp = bfs.front();
bfs.pop();
if(temp){
out<< temp -> val << “ “;
bfs.push(temp -> left);
bfs.push(temp -> right);
}
else{
out<<”null “; // 注意 null 后面有空格
}
}
return out.str(); // out 用来将树转成字符串,元素之间用空格分隔
}
// Decodes your encoded data to tree.
TreeNode deserialize(string data) {
if(data.empty()){
return nullptr; // 判空
}
istringstream in(data);
string info;
vector
while(in >> info){
if(info == “null”){ // 注意 null 后面没空格(因为空格是用来分隔字符串的,不属于字符串)
res.push_back(nullptr);
}
else{
res.push_back(new TreeNode(stoi(info)));
}
}
int pos = 1;
for(int i = 0; pos < res.size(); ++i){
// 本循环将 res 中的所有元素连起来,变成一棵二叉树
if(!res[i]){
continue;
}
res[i] -> left = res[pos++]; // pos 此时指向左子树,++后指向右子树
if(pos < res.size()){
res[i] -> right = res[pos++]; // pos 此时指向右子树,++后指向下一个节点的左子树
}
}
return res[0];
}
};
难点在于如何从序列中恢复二叉树,以前序遍历为例,先进行序列化:
//以$,来表示null
void Serialize(BinaryTreeNode pRoot,ostream& stream)
{
if(pRoot==nullptr)
{
stream<<”$,”;
return;
}
stream<
Serialize(pRoot->m_pLeft,stream);
Serialize(pRoot->m_pRight,stream);
}
再进行反序列化,利用前序遍历的特点:第一个节点为根节点,前递归左子树,再递归右子树;
void Deserialize(BinaryTreeNode* pRoot,istream& stream)
{
int number;
if(ReadStream(stream,&number))
{
pRoot =new BinaryTreeNode();
(pRoot)->m_nValue=number;
(pRoot)->m_pLeft=nullptr;
(pRoot)->m_pRight=nullptr;
Deserialize(&((pRoot)->m_pLeft),stream);
Deserialize(&((*pRoot)->m_pRight),stream);
}
}
038.字符串的排列

这其实又是全排列的问题了,递归或者DFS,建议DFS。
回溯框架参考算法手册。
//一刷 2020/12/2
//其实就是一个排列问题,那就用回溯法
class Solution {
public:
std::vector
if(s.empty()){
return {};
}
// 对字符串进行排序(以免出现重复的字符串)<br /> std::sort(s.begin(), s.end());<br /> std::vector<std::string> res;<br /> // 标记字符是否遍历过<br /> std::vector<bool> visit(s.size(), false);<br /> std::string track;<br /> backtrack(res, s, track, visit);return res;<br />}<br /> /*<br /> * 回溯函数<br /> * 使用sort函数对字符串排序,使重复的字符相邻,<br /> * 使用visit数组记录遍历决策树时每个节点的状态,<br /> * 节点未遍历且相邻字符不是重复字符时,<br /> * 则将该字符加入排列字符串中,依次递归遍历。<br /> * */<br />void backtrack(std::vector<std::string> &res, std::string s, std::string &track, std::vector<bool> &visit) {<br /> // 回溯结束条件<br /> if(track.size() == s.size()){<br /> res.push_back(track);<br /> return;<br /> }// 选择和选择列表<br /> for(int i = 0; i < s.size(); i++){<br /> // 排除不合法的选择<br /> if(visit[i]){<br /> continue;<br /> }<br /> //这一步主要是去重,如果之前已经用过了一次该元素,那就不必再用了<br /> if(i > 0 && !visit[i-1] && s[i-1] == s[i]){<br /> continue;<br /> }<br /> visit[i] = true;// 做选择<br /> track.push_back(s[i]);<br /> // 进入下一次决策树<br /> backtrack(res, s, track, visit);<br /> // 撤销选择<br /> track.pop_back();<br /> visit[i] = false;<br /> }<br />}<br />};
039.次数超过一半的数字

第一种方法,排序之后,第n/2就是;
另一个方法,n/2即是找中位数,利用快速排序的思想:随机一个数,比他小的放左边,大的放右边,如果最后该数为n/2,那就是中位数,如果不是那就从左右继续快速排序;(重点)
//我们明确这个partition函数是为了寻找中位数的index
int MoreThanHalfNum(vector
//检查非法输入
if(inputarray.size()<=1)
return 0;
int middle=inputarray.size()>>1;
int start=0;
int end=inputarray.size()-1;
int index=partition(inputarray,start,end);
while(index!=middle){
if(index>middle)//中位数在当前index的左边
{
end=index-1;//!!!!
index=partition(inputarray,start,end);
}
else{//中位数在当前index的右边
start=index+1;//!!!!
index=partition(inputarray,start,end);
}
}
return inputarray[index];
}
//输出”中位数“的index,base设置为数组第一个数字
int partitinon(vector
int base=inputarray[start];
int left=start;
int right=end+1;
while(true){
//跳过了第一个数字,因为已在base中
//从左往右找,第一个大于=base的数
while(++left<=end&&inputarray[left]
while(—right>=start&&inputarray[right]>base);
if(left>=right)
break;//没有找到
swap(inputarray[left],inputarray[right]);
}
//将base给交换到“中间”
swap(inputarray[start],inputarray[left]);
return left;
}
hash表,遍历的时候存储各个数的出现次数,当次数大于n/2,说明其出现了;
万国大战:一个数字销毁一个数字,最终剩下那个必定是超过一半的数字。
class Solution {
int m_count=0;
int m_live =INT_MAX;
public:
int majorityElement(vector
//略过判断边界条件了
for(int i=0;i
{
m_live=nums[i];
m_count++;
continue;
}
else
{
if(m_live!=nums[i]){
m_count—;
}
else{
m_count++;
}
}
}
//if(m_count>0) 必定存在
return m_live;
}
};
//这种写法更简单
int majorityElement(vector
//摩尔投票法,投我++,不投—,超过一半以上的人投我,那我稳赢哇
int count = 0, candidate = 0;
for(int n : nums)
{
if(count == 0) candidate = n;
if(n == candidate) count++;<br /> else count--;<br /> }<br /> return candidate;<br /> }
040.最小的K个数

法一,遍历比较,那就是nk的复杂度;
法二,排序,那就是nlogn;利用快排的思想
法三,类似于039的快速排序算法,将左边k变换成最小的K数(这里就不是中位数了而是第K位数);(要求修改数组)(这种类似于二分法的题目必须会!!)
vector<int> getLeastNumbers(vector<int>& arr, int k) {int n=arr.size();if(n==k) return arr;if(n<k || k<=0 || n==0) return vector<int>();int l=0,r=n-1;int index=partition(arr,l,r);while(index!=k-1){if(index>k-1) r=index-1;else l=index+1;index=partition(arr,l,r);}return vectoreturn vector<int>(arr.begin(),arr.begin()+k);}int partition(vector<int>&arr,int l,int r){int temp;//优化选取枢轴-三数取中// 或者直接取右边int mid = l + (r-l)/2;//找中位数if(arr[l]>arr[r]) swap(arr,l,r);if(arr[mid]>arr[r]) swap(arr,mid,r);if(arr[mid]>arr[l]) swap(arr,mid,l);temp = arr[l];while(l<r){while(l<r && arr[r]>=temp) r--;arr[l]=arr[r];while(l<r && arr[l]<=temp) l++;arr[r]=arr[l];}arr[l]=temp;return l;}void swap(vector<int>&arr,int l,int r){int temp = arr[l];arr[l] = arr[r];arr[r] = temp;}
法四,需要构建一个数据容器,实现删除和添加以及比较最大值:最大堆
补充:C++ 创建大顶堆和小顶堆的写法
优先队列有三个参数,其声明形式为:
priority_queue< type, container, function>。
后两个参数可以省略,第一个参数不能省略。
构建大顶堆:
priority_queue
或者:priority_queue
构建小顶堆:
priority_queue
可以使用STL中的set,或者优先队列:
vector
vector
if (k == 0) { // 排除 0 的情况
return vec;
}
priority_queue
for (int i = 0; i < k; ++i) {
Q.push(arr[i]);
}
for (int i = k; i < (int)arr.size(); ++i) {
if (Q.top() > arr[i]) {
Q.pop();
Q.push(arr[i]);
}
}
for (int i = 0; i < k; ++i) {
vec[i] = Q.top();
Q.pop();
}
return vec;
}
补充:快速排序的通用写法(可以使用部分排序的方式,即只排列k个元素)
class Solution {
public:
vector
quickSort(arr, 0, arr.size() - 1);
vector
res.assign(arr.begin(), arr.begin() + k);
return res;
}
private:
void quickSort(vector
// 子数组长度为 1 时终止递归
if (l >= r) return;
// 哨兵划分操作(以 arr[l] 作为基准数)
int i = l, j = r;
while (i < j) {
while (i < j && arr[j] >= arr[l]) j—;
while (i < j && arr[i] <= arr[l]) i++;
swap(arr[i], arr[j]);
}
swap(arr[i], arr[l]);
// 递归左(右)子数组执行哨兵划分
quickSort(arr, l, i - 1);
quickSort(arr, i + 1, r);
}
};
041.数据流中的中位数

需要构造一个存储流的数据结构,关于插入和取得中位数:

最后选择了最大堆和最小堆,如下: 
左边用最大堆,右边用最小堆,这样p1和p2指向的就是中位数了。
为了实现平均分配以及左右大小堆的一致性,插入前需要计算两边的数量。


class MedianFinder {
public:
priority_queue
priority_queue
MedianFinder() {
}
void addNum(int num) {
if(maxheap.size() == minheap.size()) {
maxheap.push(num);
minheap.push(maxheap.top());
maxheap.pop();
}
else {
minheap.push(num);
maxheap.push(minheap.top());
minheap.pop();
}
}
double findMedian() {<br /> int maxSize = maxheap.size(), minSize = minheap.size();<br /> int mid1 = maxheap.top(), mid2 = minheap.top();<br /> return maxSize == minSize ? ((mid1 + mid2) * 0.5) : mid2;<br /> }<br />};
042.连续子数组的最大和

第一种,动态规划。
先看【状态】和【选择】,简单分析之后可以这样定义:
【状态】dp[i]表示数组中以下标i结尾的最大连续子数组和;
【选择】选择下标i是否加入最大连续子数组(即更大了)。
确定了状态和选择,那么来分析状态转移:
已知i结尾的最大连续子数组和Res,
如果Res大于0,那么更新dp[i+1]为最新累加结果;
如果Res小于0,那么更新dp[i+1]为i+1的值;
class Solution {
public:
int maxSubArray(vector
if(nums.size()<=0)
return INT_MIN;
vector
//base case
dp[0]=nums[0];
//状态转移
for(int i=1;i
dp[i]=dp[i-1]+nums[i];
else
dp[i]=nums[i];
// 如果为0 那肯定就断了
}
return max_element(dp.begin(),dp.end());//学习一下这种求dp最大值的方式
}
};/
补充:获取vector中的最大值
include
max_element(dp.begin(),dp.end())
min_element(dp.begin(),dp.end())
返回的本来是迭代器的值,解引用即可拿到最大最小值;
第二种,或是探寻数组中数字规律。
以[-2,1,-3,4,-1,2,1,-5,4]为例:
初始化结果为0,最大值为0,因为-2小于0,直接跳过从下一位开始;
接着+1,结果为1,最大值暂时更新为1,接着-3,结果小于0,直接抛弃结果从+4开始重新计算。
捋一捋逻辑:
两个变量:当前结果以及当前最大值;
加一个数之后,如果结果大于最大值,则更新最大值,否则最大值不变。
如且如结果小于0,直接跳到下一位重新加(当前结果置0);
代码就出来了:
int maxSubArray(vector& nums) {
int curRes=0;
int curMax=INT_MIN;
for(auto value:nums){
curRes+=value;//依次累加
if(curRes>curMax)//最大值可能会更新
{
curMax=curRes;
}
if(curRes<=0)//连续子数组和小于0
{
curRes=0;
}
}
return curMax;
}
max_element(dp.begin(),dp.end())
min_element(dp.begin(),dp.end())
返回的本来是迭代器的值,解引用即可拿到最大最小值;
第二种,或是探寻数组中数字规律。
以[-2,1,-3,4,-1,2,1,-5,4]为例:
初始化结果为0,最大值为0,因为-2小于0,直接跳过从下一位开始;
接着+1,结果为1,最大值暂时更新为1,接着-3,结果小于0,直接抛弃结果从+4开始重新计算。
捋一捋逻辑:
两个变量:当前结果以及当前最大值;
加一个数之后,如果结果大于最大值,则更新最大值,否则最大值不变。
如且如结果小于0,直接跳到下一位重新加(当前结果置0);
代码就出来了:
int maxSubArray(vector
int curRes=0;
int curMax=INT_MIN;
for(auto value:nums){
curRes+=value;//依次累加
if(curRes>curMax)//最大值可能会更新
{
curMax=curRes;
}
if(curRes<=0)//连续子数组和小于0
{
curRes=0;
}
}
return curMax;
}
043.1~n整数中1出现的次数

第一种,遍历,时间主要耗费在求每一个数的1的个数;
第二种,1的个数即是所有个位十位百位千位```上出现1的次数的总和。
对于123456,其1的个数就是23456+1(全为0)+(23456中1出现的个数)(可以看出递归了吧)
此题暂略,意义不大。
044.数字序列中某一位的数字

法一、从1到n开始累加,知道序列化的数目相等,输出结果;
法二、数字的位数在序列化之后是有迹可循的:
0~9,10位;
10~99,902=180位;
100~999,999-100+1)3=2700位;
······
以此类推,n位数序列化具有的个数为(99999-10000+1)n(ps:99999表示n=5)。
一旦知道了这个规律,就可以知道需要找的n位数在哪个区间,找到了指定的区间即可进行进一步的细分,比如利用位运算。
注意这道题*计算长度需要用long,不然会溢出;
int findNthDigit(int n) {
if(n<0)
return -1;
int digit=1;
long length=0;
while(true){
//计算第n位有多少数字
length=countLenghtofNum(digit);
if(n
break;
}
else{
n-=length;
digit++;
}
}
return countNum(digit,n/digit,n%digit);
}
long countLenghtofNum(int num){
if(num==1)
return 10;
else
return num9pow(10,num-1);
}
int countNum(int digit,int result,int rediment){
int base=0;
if(digit!=1)
base=pow(10,digit-1);
int number=base+result;
string s_number=to_string(number);
return s_number[rediment]-‘0’;
}
045.把数组排成最小的数

隐形的大数问题,以及相互之间的大小比较问题。
对于第一个问题,使用字符串;第二个问题,字符串比较即可;
法一、全排列并比较,n!;
法二、调用sort算法,nlogn,这其实是一个隐形的排序问题,只要字符串拼接之后mn>nm,则说明n更小,应该排列在前面;(证明暂略)
string minNumber(vector
vector
string res;
for(int n : nums)
strs.push_back(to_string(n)); //将int数组转换为string数组
sort(strs.begin(), strs.end(), {return s1+s2 < s2+s1;}); //按规则排序
for(string s : strs)
res += s; //连接结果字符串
return res;
}
PS:注意自定义的字符串大小比较:
{return s1+s2 < s2+s1;}); //按规则排序
表示如果s1在前拼接小于s2在前拼接,那就将s1排在前面;
046.*把数字翻译成字符串**

法一、暴力DFS;(递归)
int backtrace(string& str, int pos) {
int n = str.size();
if (pos == n) {
return 1;
}
if (pos == n-1 || str[pos] == ‘0’ || str.substr(pos, 2) > “25”) {
return backtrace(str, pos+1);
}
return backtrace(str, pos+1) + backtrace(str, pos+2);
}
int translateNum(int num) {
string str = to_string(num);
return backtrace(str, 0);
}
法二、动态规划
用 dp[i] 来表示前 i 个数一共有多少种翻译方法。
假如第 i 个数单独翻译,那么 dp[i] = dp[i - 1]。
假如第 i 个数与第 i - 1 个数组合翻译,那么有两种情况:
两个数的组合处于 [10, 25] 的区间,那么既可以组合翻译,又可以单独翻译,则 dp[i] = dp[i - 2] + dp[i - 1]。
两个数的组合不在 [10, 25] 的区间,那么组合失败,还是得单独翻译,也就是与第 2 点一样。所以 dp[i] = dp[i - 1]。
综上所述,当两个数的组合处于 [10, 25] 的区间,dp[i] = dp[i - 2] + dp[i - 1];当两个数的组合不在 [10, 25] 的区间,dp[i] = dp[i - 1]。(状态转移方程)
int translateNum(int num) {
if(num < 10) {return 1;}
string s = to_string(num);<br /> int len = s.length();<br /> vector<int> dp(len + 1);<br /> dp[1] = 1; // 显而易见 dp[1] = 1<br /> dp[0] = 1; // 比如 num = 12,有两种方法,即 dp[2] = dp[1] + dp[0],可得 dp[0] = 1for(int i = 2; i < len + 1; ++i) {<br /> if(s[i - 2] == '1' || (s[i - 2] == '2' && s[i - 1] <= '5')) {<br /> dp[i] = dp[i - 2] + dp[i - 1];<br /> }<br /> else {<br /> dp[i] = dp[i - 1];<br /> }<br /> }return dp[len];<br /> }<br />法三、从右到左(自下而上)来进行翻译,简短的思路:<br />1.每次取最后两位数,rem = num % 100<br />2.若rem > 25,则无法表示,即rem的个位和十位无法合一起,则用translateNum(num/10),表示前进一位<br />3.若在00 <= rem <= 09,则无法表示,即rem的个位和十位无法合一起,所以用translateNum(num/10)<br />如num = 506,其只有一种表示为fag,不可表示为fg,所以0是无法和6组合一起成为06<br />4.若在10 <= rem <= 25,则可以分出两种表示方法,所以用translateNum(num/10) + translateNum(num/100)递归来计算数量<br />5.所以总结一下就是:<br />**if (num < 10),则加1**<br />**if (num%100 < 10 || num%100 > 25) translateNum(num/10);**<br />**if (10 <= num % 100 <= 25) translateNum(num/10) + translateNum(num/100);**<br />if (num < 10),则加1<br />if (num%100 < 10 || num%100 > 25) translateNum(num/10);<br />if (10 <= num % 100 <= 25) translateNum(num/10) + translateNum(num/100);
class Solution {
public:
int translateNum(int num) {
if (num < 10) return 1;
return (num%100 < 10 || num%100 > 25) ? translateNum(num/10) : translateNum(num/10) + translateNum(num/100);
}
};
047.礼物的最大价值

典型的动态规划,开始设想dp[i]表示i步能获取的最大值,但是这样根本分析不下去。
设置二维dpi,表示到达(i,j)时获取的最大礼物数目,于是状态转移方程出来了:
dpi=max(dpi-1+dpi)+gifti;
ps:注意礼物的边界条件,如果到达最下或最右,那就只能向右或向下,因此需要设置判断条件。(也可以通过多开一列的空间来进行)
代码已手撸:
int maxValue(vector
if(grid.size()<1)
return -1;
vector
vector
int h=grid.size();
int w=grid[0].size();
for(int i=0;i
dp[i][j]=grid[i][j];//base case
else
{
//注意三边界
if((i-1)<0&&(j-1)>=0)
dp[i][j]=dp[i][j-1]+grid[i][j];
else if((i-1)>=0&&(j-1)<0)
dp[i][j]=dp[i-1][j]+grid[i][j];
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1])+grid[i][j];
}
}<br /> }<br /> return dp[h-1][w-1];<br /> } <br />还可以将二维表给压缩一下,因为**只跟上两步的结果有关**,保存一下即可,**还可以原地dp直接修改grid(即将结果设置进grid)**)。<br />int maxValue(vector<vector<int>>& grid) {<br /> int m = grid.size(), n = grid[0].size();<br /> vector<int> dp(n+1,0);<br /> for(int i = 1; i <= m; i++)<br /> for(int j = 1; j <= n; j++)<br /> dp[j] = max(dp[j - 1], dp[j]) + grid[i - 1][j - 1];<br /> //等号右边的dp[j-1]是当前行左边的值,dp[j]是当前列上一行的值,等号左边的dp[j]是当前要更新的值<br /> return dp[n];<br />}
048.最长不含重复字符的子字符串

滑动窗口(双指针),维持一个数组记录出现的次数,遇到重复字母则更新一下最大长度。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int map[128] = {0}, len = 0, start = 0; //map统计字符在当前子串出现次数,字符的ascii码值小于128
for(int i = 0; i < s.size(); ++i)
{
++map[s[i]];
while(map[s[i]] == 2) //出现重复
—map[s[start++]]; //不断滑动右移的同时恢复map中的状态,当map[s[i]]=1时,确定新的start
len = max(len, i - start + 1);
}
return len;
}
};
049.丑数

法一、遍历判断是否只有2 3 5的因子;时间效率不是很高;
int nthUglyNumber(int n) {
if (n <= 6) {return n;}
int count = 6, i = 7;<br /> //这种方法是从7开始看到底哪些数字是丑数<br /> while (true) {<br /> if (determine(i)) {++ count;}<br /> //当丑数的个数已经达到n时,说明找到了该丑数<br /> if (count == n) {break;}<br /> ++ i;<br /> }return i;<br /> }<br /> //根据235因子来判断是否为丑数<br /> bool determine(int num) {<br /> if (num > 0 && num <= 6) {return true;}<br /> else if (num <= 0) {return false;}while (num % 3 == 0) {num /= 3;}<br /> while (num % 5 == 0) {num /= 5;}<br /> while (num % 2 == 0) {num /= 2;}return (num == 1);<br /> }<br />法二、利用空间换时间,**后面一个丑数肯定是前一个丑数乘以2或3或5**,因此需要记录一下该因子使用过的次数(也可以直接使用优先队列或是大堆来进行);<br />int nthUglyNumber(int n) {<br /> int two=0;<br /> int three =0;<br /> int five=0;<br /> vector<int> storeugly(n);<br /> storeugly[0]=1;for(int i=1;i<n;i++){<br /> //这是三个候选人<br /> int t2=storeugly[two]*2;<br /> int t3=storeugly[three]*3;<br /> int t5=storeugly[five]*5;<br /> //这是在进行候选人选举,选举之后其推荐者获得伯乐奖(+1)<br /> int tp=min(min(t2,t3),t5);<br /> if(tp==t2)two++;<br /> if(tp==t3)three++;<br /> if(tp==t5)five++;storeugly[i]=tp;<br /> }<br /> return storeugly[n-1];<br /> }
050.第一个只出现一次的字符

法一、hash表(或数组[26])记录一下出现的次数即可;
class Solution {
public:
char firstUniqChar(string s) {
int m[26] = {0};
//遍历记录所有字符出现的次数
for(char c : s)
++m[c-‘a’];
//找到第一个只出现了一次的字符(从前往后)
for(char c : s)
if(m[c-‘a’] == 1) return c;
return ‘ ‘;
}
};
相比于题目一,这个问题需要考虑后续增加的字符造成之前的字符被覆盖。

051.数组中的逆序对

法一、暴力解法,遍历为(n-1)!;
法二、其实是一种分治的思想,自顶向下的推理,自底向上的计算。
052.两个链表的第一个公共节点

法一、hash表,两个指针分别从开头遍历两个链表,将各个节点加入同一个链表;
法二、利用栈使用从尾到头比较,最后一个相同的节点就是公共节点;
法三、快慢指针,先分别遍历两个链表,求出其长度m,n,让长链表先走m-n步,而后遍历遇到的第一个相同节点就是公共节点;
class Solution {
public:
ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode curA = headA;
ListNode curB = headB;
int lenA = 0, lenB = 0;
while (curA != NULL) { // 求链表A的长度
lenA++;
curA = curA->next;
}
while (curB != NULL) { // 求链表B的长度
lenB++;
curB = curB->next;
}
curA = headA;
curB = headB;
// 让curA为最长链表的头,lenA为其长度
if (lenB > lenA) {
swap (lenA, lenB);
swap (curA, curB);
}
// 求长度差
int gap = lenA - lenB;
// 让curA和curB在同一起点上(末尾位置对齐)
while (gap—) {
curA = curA->next;
}
// 遍历curA 和 curB,遇到相同则直接返回
while (curA != NULL) {
if (curA == curB) {
return curA;
}
curA = curA->next;
curB = curB->next;
}
return NULL;
}
};
另外一种双指针解法,即利用如果存在公共节点,那么当一个指针从A遍历到尾,又开始从B走;另一个指针从B遍历到尾,又开始从A。最终会相遇在公共节点,否则就会返回null(因为此时两个链表其实都是指向最后的null节点了)。
a+(b-c)==b+(a-c)
class Solution {
public:
ListNode getIntersectionNode(ListNode headA, ListNode headB) {
auto p1 = headA, p2 = headB;
while (p1 != p2) //最终p1和p2走的路径长度是相等的<br /> {<br /> if (p1) p1 = p1->next;<br /> else p1 = headB;if (p2) p2 = p2->next;<br /> else p2 = headA;<br /> }return p1;<br /> }<br />};
053.在排序数组中查找数字

法一、遍历;时间复杂度n
法二、二分法,时间复杂度logn(因为我只需要找一个数)找到开头或者结尾坐标即可,然后我从这个开头结尾处遍历,就很简单了,代码见下:
class Solution {
public:
int search(vector
if (nums.size() == 0) {
return 0;
}
int left = 0, right = nums.size() - 1;<br /> int count = 0;<br /> <br /> //这个是为了找到开始的节点位置<br /> while (left < right) {<br /> int mid = (left + right) / 2;<br /> //这里之所以取等,是因为我们想找的是<br /> //连续相同数字的左边界<br /> if (nums[mid] >= target) {//找到与之相同元素的区间<br /> right = mid;<br /> }<br /> else {<br /> left = mid + 1;<br /> }<br /> }<br /> //这里可以再优化一下,即如果不等,那就break<br /> for (int i = left; i < nums.size(); ++i) {<br /> if (nums[i] == target) {<br /> ++ count;<br /> }<br /> }return count;<br /> }<br />};<br />法三、递归,**拆分成找左右两边数字的个数**,结合二分的思想来优化,代码如下:<br />int getnum(int []nums, int left, int right, int target)<br />{<br /> int mid = left + (right - left)/2;<br /> //base case递归终点<br /> if(left > right) return 0;<br /> else if(left == right) return (nums[mid]==target)?1:0;<br /> //单步递归子问题及综合<br /> if(nums[mid] > target) return getnum(nums, left, mid-1, target);<br /> else if(nums[mid] < target) return getnum(nums, mid+1, right, target);<br /> else if(nums[mid]==target) return <br /> getnum(nums, mid+1, right, target) + getnum(nums, left, mid-1, target) + 1;<br />}<br /><br />法一、遍历,因为下标和数字应该相等才对,**从0开始遍历加1递增**;<br />法二、二分查找,**寻找第一个不等于下标的数字,**只需要判断大于或者等于即可。<br />class Solution {<br />public:<br /> int missingNumber(vector<int>& nums) {<br /> if(nums.size()<1)<br /> return -1;<br /> int left=0;<br /> int right=nums.size()-1;<br /> int mid;<br /> //二分查找偏移<br /> while(left<=right){<br /> mid =left+(right-left)/2;//中点<br /> if(nums[mid]==mid)//左半部分没毛病,错位的在右边<br /> {<br /> if(mid+1>nums.size()-1)<br /> return mid+1;<br /> left=mid+1;<br /> continue;<br /> }<br /> else if(nums[mid]>mid){//左边有一个地方错位了<br /> //小心翼翼地移动一步<br /> if(mid-1<0)<br /> return mid; <br /> if(nums[mid-1]==mid-1)<br /> return mid;<br /> right=mid-1;<br /> continue;<br /> }<br /> }<br /> return mid;<br /> }<br />};<br /><br />法一、遍历;<br />法二、**二分查找**,如果nums[mid]<mid,那就查找右半边;如果nums[mid]>mid,查找左半边。(如果你前面的人都跟不上潮流,那么你也无法跟上)<br />class Solution {<br />public:<br /> int missingNumber(vector<int>& nums) {<br /> if(nums.size()<1)<br /> return -1;<br /> int left=0;<br /> int right=nums.size()-1;<br /> int mid;<br /> //二分查找偏移<br /> while(left<=right){<br /> mid =left+(right-left)/2;//中点<br /> if(nums[mid]==mid)//芜湖!恰好命中!<br /> {<br /> return mid+1<br /> }<br /> else if(nums[mid]>mid){//右边命中无望<br /> //小心翼翼地移动一步<br /> if(mid-1<0)<br /> return mid; <br /> //居然中了!?<br /> if(nums[mid-1]==mid-1)<br /> return mid;<br /> right=mid-1;<br /> continue;<br /> }<br /> else if(nums[mid]<mid)//左边命中无望<br /> {<br /> //小心翼翼地移动一步<br /> if(mid+1>nums.size()-1)<br /> return mid; <br /> //居然中了!?<br /> if(nums[mid-1]==mid-1)<br /> return mid;<br /> left=mid+1;<br /> continue;<br /> }<br /> }<br /> return mid;<br /> }<br />};
054.**二叉搜索树的第K大节点**
<br /> 法一,二叉搜索树,**中序遍历就是一个从小到大的排序数组**。找第K大,那就先遍历再输出对应位置的数字即可。<br /> //正解:要想找第n大,只能先将二叉树变成一个数组,从中提取出想要的数<br />class Solution {<br /> vector<int> res;<br />public:<br /> void preCycle(TreeNode* root){<br /> if(root==NULL)<br /> return;<br /> preCycle(root->left);<br /> res.push_back(root->val);<br /> preCycle(root->right);<br /> return;<br /> }<br /> int kthLargest(TreeNode* root, int k) {<br /> //1.边界条件<br /> if(root==NULL||k==0)<br /> return 0;<br /> //2.进行前序遍历<br /> preCycle(root);<br /> return res[res.size()-k];<br /> }<br />};<br />法二、对中序遍历进行改造,变成右、中、左,这样就是一个从大到小的序列。<br />class Solution {<br /> int cur=0;<br /> int m_k;<br />public:<br /> void preCycle(TreeNode* root,int &n){<br /> if(root==NULL)<br /> return;<br /> preCycle(root->right,n);<br /> cur++;<br /> if(cur==m_k)<br /> {<br /> n=root->val;<br /> return ;<br /> }<br /> preCycle(root->left,n);<br /> return;<br /> }<br /> int kthLargest(TreeNode* root, int k) {<br /> //1.边界条件<br /> if(root==NULL||k==0)<br /> return 0;<br /> //2.进行<br /> int n;<br /> m_k=k;<br /> preCycle(root,n);<br /> return n;<br /> }<br />};
055.**二叉树的深度**

法一、二叉树的深度其实就是左右子树的最大深度**+1*,那么这就变成了一个简单的递归问题(DFS)。
class Solution {
public:
int maxDepth(TreeNode root) {
if(NULL==root)
return 0;
return max(maxDepth(root->left),maxDepth(root->right))+1;
}
};
法二、也可以用BFS层序遍历,利用队列来实现。
int maxDepth(TreeNode root) {
if(root == NULL) return 0;
queue<TreeNode >q;
q.push(root);
int depth = 0;
while(!q.empty())
{
++depth;//每处理完一层的元素就+1
int count = q.size(); //保存每一层元素个数
while(count—)
{
TreeNode* temp = q.front();
q.pop();
if(temp->left) q.push(temp->left);<br /> if(temp->right) q.push(temp->right);<br /> }<br /> }<br /> return depth;<br /> } <br /><br /> 法一、递归调用题目一的计算深度的函数,**但是这会造成递归栈溢出;**<br />法二、利用**后序遍历,自下而上的记录各节点的深度**。<br />bool isBalanced(TreeNode* root)<br />{<br /> if (root == nullptr) return true;<br /> int depth = 0;<br /> return isBalanced(root, depth);<br />}
bool isBalanced(TreeNode* root,int &pDepth) {
if (root == nullptr) { pDepth = 0; return true; }
int left=0,right=0;
if (isBalanced(root->left, left) && isBalanced(root->right, right))
{
int diff = left - right;
if (abs(diff) <= 1)
{
pDepth = 1 + (left > right ? left : right);
return true;
}
}
return false;
}
056.**数组中出现两次**
<br /> 法一、暴力求解;<br />法二、异或求解。<br /> 先对所有数字进行一次异或,得到**两个出现一次的数字的异或值**。在异或结果中找到**任意为1** 的位。根据这一位对所有的数字进行分组。**在每个组内进行异或操作,得到两个数字**。<br /> 这种分组之后能够找出的原理是:**两个相同数在同一位置肯定相同,两个不相同的数字既然异或不为0那么必然在这一位是不同的。**<br />class Solution {<br />public:<br /> vector<int> singleNumbers(vector<int>& nums) {<br /> int ret = 0;<br /> for (int n : nums)<br /> ret ^= n;<br /> int div = 1;<br /> while ((div & ret) == 0)<br /> div <<= 1;<br /> int a = 0, b = 0;<br /> for (int n : nums)<br /> if (div & n)<br /> a ^= n;<br /> else<br /> b ^= n;<br /> return vector<int>{a, b};<br /> }<br />};<br /><br />法一、hash表;<br />法二、排序再查找; <br />法三、但是可以**考虑用位的操作来解题:如果出现了某一位能被****3整除,则该位为0,否则为1。而后将对应位置这么设置即可。**<br />class Solution {<br />public:<br /> int singleNumber(vector<int>& nums) {<br /> vector<int> bits(32,0);<br /> for(auto num : nums) {<br /> for(int i=0;i<32;i++) {<br /> bits[i] += num & 1;<br /> num >>= 1;<br /> }<br /> }<br /> int res = 0;<br /> //从位数开始计算<br /> for(int i=31; i>=0; i--) {<br /> res <<= 1;<br /> res += bits[i] % 3;<br /> }<br /> return res;<br /> }<br />};
057.**和为s的数字**

一开始通过s=a+b,想到a=s-b,所以直接遍历数组寻找是否存在对应的值即可,但是时间复杂度贼高,n平方。不过基于这种想法可以利用双指针,提高搜索速度。(加上这个数组是排序的,根据和的**target的大小关系可以更轻松地确定指针前进的方向)
class Solution {
public:
vector
if (nums.size() == 1) {
return {};
}
int i = 0, j = nums.size() - 1;
while (i < j) {
if (nums[i] + nums[j] == target) {
return {nums[i], nums[j]};
}
else if (nums[i] + nums[j] < target) {
++ i;
}
else {
— j;
}
}
return {};
}

如果问到这个题当场暴毙啊······
借鉴上一个问题(虽然没有说数组是排序递增的,但是连续序列就隐含了是一个递增的数组)同样利用双指针,不过这里的双指针不是代表两个数字,而是代表区间的端点:
如果当前区间的和小于目标值,则区间端点向右移动;
那么终止条件是什么呢?
当区间的长度为**1(或是最小值已经超过目标一半),则说明已经找不到其他的元素了。
这种双指针确定区间的题太妙了吧!
vector
int i = 1; // 滑动窗口的左边界
int j = 1; // 滑动窗口的右边界
int sum = 0; // 滑动窗口中数字的和
vector
while (i <= target / 2) {
if (sum < target) {
// 右边界向右移动,增大区间序列
sum += j;
j++;
} else if (sum > target) {
// 左边界向右移动,减小最小值
sum -= i;
i++;
} else {
// 记录结果
vector
for (int k = i; k < j; k++) {
arr.push_back(k);
}
res.push_back(arr);
// 左边界向右移动
sum -= i;
i++;
}
}
return res;
}
058.**反转字符串**

一种解法是先反转**整体字符串,而后再顺序翻转每个单词即可;
PS:
erase函数的原型如下:
(1)string& erase ( size_t pos = 0, size_t n = npos );
(2)iterator erase ( iterator position );
(3)iterator erase ( iterator first, iterator last );
也就是说有三种用法:
(1)erase(pos,n); 删除从pos开始的n个字符,比如erase(0,1)就是删除第一个字符
(2)erase(position);删除position处的一个字符(position是个string类型的迭代器)
(3)erase(first,last);删除从first到last之间的字符(first和last都是迭代器**)
class Solution {
public:
string reverseWords(string s) {
if (s.length() == 1 && s[0] == ‘ ‘) {
// 特殊情况:直输入一个空格(s = “ “),返回空字符串
return “”;
}
trim(s); // 先去除 s 首尾的空格
reverse(s, 0, s.length() - 1); // 将整个 s 翻转
int i = 0, j = 0; // i 和 j 用于定位一个单词的首和尾(左闭右闭)
while (j < s.length()) {
if (s[j] != ‘ ‘) {
j++;
if (j == s.length()) {
// 如果此时是最后一个单词,那么 j 此刻等于 s.length()
// 为避免直接退出循环而导致最后一个单词没有被处理,于是在此手动处理
reverse(s, i, j - 1);
break;
}
}
else { // j 当前指向空格
reverse(s, i, j - 1); // 翻转 [i, j - 1] 区间内的单词
j++; // 看当前空格后面还有没有多余的空格
while (j < s.length() && s[j] == ‘ ‘) {
s.erase(j, 1);
}
i = j; // i 定位到下一个单词的起始处
}
}
return s;
}
void trim(string& str) {
// 去除一个字符串首尾的空格
if (str.empty()) {
return;
}
str.erase(0, str.find_first_not_of(' '));<br /> str.erase(str.find_last_not_of(' ') + 1);<br /> }<br /> void reverse(string& str, int start, int end) {<br /> // 翻转一个字符串<br /> if (end - start < 1 || end >= str.length()) {<br /> return;<br /> }<br /> while (start < end) {<br /> char temp = str[start];<br /> str[start] = str[end];<br /> str[end] = temp;<br /> start++; end--;<br /> }<br /> }<br />};<br /> **另一种解法****双指针,寻找空格而后利用string的子串特性将其提取出来;**<br />class Solution {<br />public:<br /> string reverseWords(string s) {<br /> //边界条件<br /> int len = s.length();<br /> if (len == 0) {<br /> return "";<br /> }<br /> int j = len - 1;<br /> string res = "";<br /> while (j >= 0) {<br /> if (s[j] == ' ') {<br /> // 当 s[j] 是空格时,j 不断左移<br /> j--;<br /> continue;<br /> }<br /> while (j >= 0 && s[j] != ' ') {<br /> // 注意 while 里必须用 && 短路求值,且 j >= 0 要放前面<br /> // 不然如果 j 变成 -1,那么计算 s[j] 会发生溢出错误!<br /> j--;<br /> }<br /> int pos = j; // 用 pos 保存 j 当前的位置<br /> j++; // j 现在指向的是一个空格,需要右移一位才能指向一个单词的开头<br /> //其实就是找到每个单词的开头 然后进行拷贝<br /> while (s[j] != ' ' && j < len) {<br /> // 向 res 中添加单词<br /> res += s[j];<br /> j++;<br /> }<br /> j = pos; // j 回到新添加的单词的最左端再往左一个空格处<br /> res += ' '; // 单词添加完毕后需要加上一个空格<br /> }<br /> if (res[res.length() - 1] == ' ') {<br /> // 删除 res 最后一位的多余空格<br /> res.erase(res.length() - 1, 1);<br /> }<br /> return res;<br /> }<br />};<br />**又想到一种,每个字符串压入栈,到末尾之后出栈结合;**<br /><br /> **这道题是上一道题的进阶版:将上题的法一应用到该题,需要旋转的部分和后续部分分为两个部分,而后先旋转所有,再分辨旋转前后两个部分,即可完成题目要求(这个需要实际遇到的时候推导一遍其特性);**<br /> **也可以利用切片的思想,将旋转部分和后续部分分别切片再倒序拼接即可,实际实现过程使用****erase和+;**
059.**队列的最大值**
<br /> **需要****滑几次?nums-window+1次;**<br /> 考虑到窗口移动之后也许最大值已经出去了,所以动态维护一个数据结构,**可以获取最大值及其下标,发现可以用双端队列**:<br />每次加入新值,就实行末尾淘汰;**而后判断当前最大值是否已经超限,超限就弄出去!(注意边界条件!!)**<br />[https://leetcode-cn.com/problems/hua-dong-chuang-kou-de-zui-da-zhi-lcof/](https://leetcode-cn.com/problems/hua-dong-chuang-kou-de-zui-da-zhi-lcof/)<br />写的最简洁:<br />
补充:deque双端队列的用法
deque.push_back(elem); //在容器尾部添加一个数据
deque.push_front(elem); //在容器头部插入一个数据
deque.pop_back(); //删除容器最后一个数据
deque.pop_front(); //删除容器第一个数据
deque.at(idx); //返回索引idx所指的数据,如果idx越界,抛出out_of_range。
deque[idx]; //返回索引idx所指的数据,如果idx越界,不抛出异常,直接出错。
deque.front(); //返回第一个数据。
deque.back(); //返回最后一个数据
需要使用两个双端队列。
//两个双端队列
//一个存储原数据
//一个存储最大值数据,每压入一个数据,可能的最大值都会变化,所以需要存储
class MaxQueue {
public:
MaxQueue() {
}
int max_value() {
if (q2.empty()) return -1;
return q2.front();
}
void push_back(int value) {
// q1 push
q1.push_back(value);
// q2 push
while (!q2.empty() && q2.back() < value)
{
q2.pop_back();
}
q2.push_back(value);
}
int pop_front() {
if (q1.empty()) return -1;
else
{
if (q1.front() == q2.front()) q2.pop_front();
int popvalue = q1.front();
q1.pop_front();
return popvalue;
}
}
private:
deque
};
060.n个骰子的点数

法一、递归,n n-1 n-2,耗时太长了。
法二、动态规划,dpi表示投掷i个骰子时,点数为j的次数,故状态转移方程即是:
dpi += dpi - 1(k属于1-6,即进行一个模拟运算)
vector
int dp[15][70];
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= 6; i ++) {
dp[1][i] = 1;
}
//这个状态转移才是重点
for (int i = 2; i <= n; i ++) {
for (int j = i; j <= 6i; j ++) {
for (int cur = 1; cur <= 6; cur ++) {
if (j - cur <= 0) {
break;
}
dp[i][j] += dp[i-1][j-cur];
}
}
}
//这个主要是为了算概率的
int all = pow(6, n);
vector
for (int i = n; i <= 6
ret.push_back(dp[n][i] * 1.0 / all);
}
return ret;
}
061.扑克牌中的顺子

法一、排序,记录0的个数,从头至尾遍历,如果某一个数不等于前一个+1,就用0补上,如果0不够就报错;
class Solution {
public:
bool isStraight(vector
sort(nums.begin(), nums.end()); // 先对 nums 升序排序
int countZero = 0; // 用于计算 0 的个数
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] == 0) {
countZero++;
continue;
}
int j = i + 1;
if (j < nums.size()) {
if (nums[j] == nums[i]) {
// 如果相邻两个元素相等,就不是顺子
return false;
}
//女娲补天!!!
int temp = nums[j] - nums[i];
while (temp > 1) {
if (countZero == 0) {
// 0 如果不够用了,false
return false;
}
countZero—; // 相邻两个数的差距用 0 来弥补
temp—; // 差距减小 1
}
}
}
return true;
}
};
法二、换一种思路,判断条件是最大牌-最小牌(去除0,且非重复)<5,**即说明可以排序**;(且无重复的非0元素)
class Solution {
public:
bool isStraight(vector
bool m[15]={false};
int minValue = 14, maxValue = 0;
for (int item : nums) {
if (item == 0) {
continue;
}
if (m[item]) {
return false;
}
m[item] = true;
minValue = min(minValue, item);
maxValue = max(maxValue, item);
}
//只要最大牌和最小牌之间的差距小于等于五即可
return maxValue - minValue + 1 <= 5;
}
};
062.圆圈中最后剩下的数字

约瑟夫环问题;
法一、环形链表模拟,时间复杂度为mn;
法二、动态规划(最强解法)
最终剩下一个人时的安全位置肯定为0,反推安全位置在人数为n时的编号:
人数为1: 0
人数为2: (0+m) % 2
人数为3: ((0+m) % 2 + m) % 3
人数为4: (((0+m) % 2 + m) % 3 + m) % 4
迭代至n即可。
这里的 +m 可以理解为向右移动 m 位,取余是在到达尾部还需移动时,将其移到首位。
class Solution {
public:
int lastRemaining(int n, int m) {
int pos = 0; // 最终活下来那个人的初始位置
for(int i = 2; i <= n; i++){
pos = (pos + m) % i; // 每次循环右移
}
return pos;
}
};
F063.股票的最大利润

法一、从后往前逆推寻找最大值,有点像是单调栈;(或是从前往后,记录最小值,那么就可得知当前卖出获利多少)
class Solution {
public:
int maxProfit(vector
if(prices.size()<2)
return 0;
int high=-1;
int low=-1;
int tempmax=0;
for(int i=prices.size()-1;i>=0;i—){
if(prices[i]>=high)//比最大值还要大,则说明在之前卖出收益更高
{
high=prices[i];
low=prices[i];//仔细想想这步
continue;
}
else if(prices[i]<=low){//比最小值还小,说明在这买入更划算
low=prices[i];
if((high-low)>tempmax)
tempmax=high-low;
}
}
return tempmax;
}
}
法二、动态规划,状态 选择 转移;dpi表示第i天持有或没持有股票时的现金数;
PS:可以进行压缩哈,因为只需要昨天的两个值
class Solution {
public:
int maxProfit(vector
if(prices.size()<=0)
return 0;
vector
for(int i=0;i
{
dp[i][0]=0;//第一天没买入利润就是0
dp[i][1]=-prices[i];//其实就是第一天就买入
continue;
}
//木有股票
dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]);
//有股票
dp[i][1]=max(dp[i-1][1],-prices[i]);
}
//这个返回才是神来之笔!!!
return dp[prices.size()-1][0];//想想为什么返回0?肯定卖出去过后的收入更多啊!
}
064.求1+2+….n

法一、利用类的静态变量,创建n个对象,秀的头皮发麻(Temp p=new Temp[n]);
法二、利用虚函数实现对递归的选择!
法三、利用函数指针实现上述功能(参加剑指offer328页)
法四、利用&&运算来实现递归的返回:
*由于&&的特性,最后一步时,直接返回0;
法五、sizeof特性,然后连加特性
class Solution {
public:
int sumNums(int n) {
bool a[n][n+1];
return sizeof(a)>>1;
}
};
065.不用加减乘除做加法

无进位和 与 异或运算规律相同。
//只能用位运算咯
class Solution {
public:
int add(int a, int b) {
if (a == 0 || b == 0) {
return a == 0 ? b : a;
}
int sum = 0, carry = 0;
while (b != 0) { // 当没有进位的时候退出循环
sum = a ^ b; //异或代表不带进位的加法
//主要看书是否有进位
carry = (unsigned int) (a & b) << 1;
// C++ 不允许负数进行左移操作,故要加 unsigned int
//将进位取出来即可
a = sum;
b = carry;
}
return a;<br /> }<br />};
如何利用位运算实现交换两个数的值呢?
**066.构建乘积数组

法一、定义一个输出数组,先记录左边的乘积,再从右向左遍历,逐个乘以右边的乘积,最后返回输出数组
class Solution {
public:
vector
int n = a.size(), right = 1;
vector
for(int i = 1; i < n ; ++i)
B[i] = B[i-1] a[i-1]; //此时B[i]记录i左边的乘积,B[0] = 1(占位符都是1)
//之所以是n-2
//因为最后一排没有右边!!!
for(int i = n-2 ; i >= 0 ; —i)
{
right = a[i+1];//right记录i右边的乘积
B[i] = B[i] right;//结果 = 左边乘积右边乘积
}
return B;
}
};
067.字符串转换为整数
这道题的难点在于考虑所有的特殊条件,这在面试的时候需要跟面试官积极交流,看看他的需求是什么!
答:看剑指offer上的解答;
int strToInt(string str) {
int i = 0, flag = 1;
int res = 0; //默认flag = 1,正数
//去除头部的空格
while (str[i] == ‘ ‘) i ++;
//找到正负号(正号没考虑)
if (str[i] == ‘-‘) flag = -1;
if (str[i] == ‘-‘ || str[i] == ‘+’) i ++;
for (; i < str.size() && isdigit(str[i]); i ++) {
if (res > INT_MAX / 10 || (res == INT_MAX / 10 && str[i] - ‘0’ > 7)) //溢出判定
return flag == 1 ? INT_MAX : INT_MIN;
res = res 10 + (str[i] - ‘0’);
}
return flag res;
}
068.树中两个节点的最近公共祖先
题目一、二叉搜索树的最近公共祖先
二叉搜索树的性质,除了有中序遍历是升序之外,还有就是它满足二分搜索,如果我们将root到两个节点的路径保存到容器中,一一比对,就可以找到最近的公共祖先(找到相同之后,第一个不同)。
PS:对于这个容器,hash表最快,vector也是可以的。
class Solution {
public:
vector
vector
TreeNode* node = root;
while (node != target) {
path.push_back(node);
if (target->val < node->val) {
node = node->left;
}
else {
node = node->right;
}
}
path.push_back(node);
return path;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {<br /> vector<TreeNode*> path_p = getPath(root, p);<br /> vector<TreeNode*> path_q = getPath(root, q);<br /> TreeNode* ancestor;<br /> for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) {<br /> if (path_p[i] == path_q[i]) {<br /> ancestor = path_p[i];//一直更新祖先节点<br /> }<br /> //一旦不等,那就说明找到了最近的祖先<br /> else {<br /> break;<br /> }<br /> }<br /> return ancestor;<br /> }<br />};
题目二、二叉树的最近公共祖先
普通的二叉树没有办法快速地找到父节点至其的路径,这道题有两种思路,一种是基于DFS(类前序遍历,找到结果就回去);另一种是基于递归的后序遍历。
递归法:解释,主要是对左右子树进行pq的寻找,详解如下:
class Solution {
public:
TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (!root || !p || !q || p == root || q == root) {
return root;
}
TreeNode leftTree = lowestCommonAncestor(root -> left, p, q);
TreeNode rightTree = lowestCommonAncestor(root -> right, p, q);
if (!leftTree && !rightTree) {
return nullptr; // 左边没找到右边也没找到
} else if (leftTree && rightTree) {
return root; // 左边找到了右边也找到了
} else if (!leftTree && rightTree) {
return rightTree; // 左边没找到右边找到了
} else {
return leftTree; // 左边找到了右边没找到
}
}
};
这个是进阶版本的代码:
class Solution {
public:
TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == NULL)return NULL;
if(root == p||root == q)return root;
TreeNode left = lowestCommonAncestor(root->left, p, q);
TreeNode right = lowestCommonAncestor(root->right, p, q);
if(left && right)return root;
return left ? left : right; // 只有一个非空则返回该指针,两个都为空则返回空指针(这逻辑无敌了!!)
}
};
另一种则是类前序,代码过于复杂,不建议:
class Solution {
public:
TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (!root || !p || !q || p ==root || q == root) {
return root;
}
vector<TreeNode*> pPath;<br /> vector<TreeNode*> qPath;getNodePath(root, p, pPath); // 找到从 root 到 p 的路径<br /> getNodePath(root, q, qPath); // 找到从 root 到 q 的路径return getlowestCommonAncestor(pPath, qPath); // 返回两条路径上最后一个相同的节点<br /> }void getNodePath(TreeNode* root, TreeNode* node, vector<TreeNode*>& path) { // 注意传引用<br /> if (!root || !node) {<br /> return;<br /> }TreeNode* temp = root, *prev = nullptr;<br /> deque<TreeNode*> store;while (temp || !store.empty()) {<br /> while (temp) {<br /> store.push_back(temp);if (temp == node) { // 中<br /> while (!store.empty()) {<br /> // 如果 root 匹配到了 node,填充 path 并退出函数<br /> TreeNode* t = store.front();<br /> path.push_back(t);<br /> store.pop_front();<br /> }<br /> return;<br /> }temp = temp -> left; // 左<br /> }temp = store.back();if (!temp -> right || temp -> right == prev) {<br /> // 如果 temp 没有右子节点,或者我们之前已经访问过其右子节点了<br /> store.pop_back();<br /> prev = temp;<br /> temp = nullptr; // 这样就可以不进入上面那个 "while (temp)" 的子循环了<br /> } else {<br /> temp = temp -> right; // 右<br /> }<br /> }<br /> }TreeNode* getlowestCommonAncestor(vector<TreeNode*>& path1, vector<TreeNode*>& path2) { // 注意传引用<br /> if (path1.empty() || path2.empty()) {<br /> return nullptr;<br /> }int size = min(path1.size(), path2.size());<br /> int i = 0;for (; i < size; ++i) {<br /> if (path1[i] == path2[i]) {<br /> continue;<br /> } else {<br /> break; // 两条路径上的节点第一次不相同时,退出<br /> }<br /> }<br /> return path1[i - 1]; // 返回两条路径上最后一次相同的节点<br /> }<br />};
二叉树中和为某一值的路径
这个路径,指的是从根到叶子节点。
利用前序遍历即是路径可解。(其实就是回溯法)
class Solution {
private:
vector
vector
public:
vector
if(!root) return {};
recursion(root, sum);
return res;
}
void recursion(TreeNode root, int sum)
{
if(!root) return;
temp.push_back(root -> val);
sum -= root -> val;
if(sum == 0 && !root -> left && !root -> right)
res.push_back(temp);
recursion(root -> left, sum); // 左
recursion(root -> right, sum); // 右
temp.pop_back(); // 函数退出之前先弹出当前节点
}
};