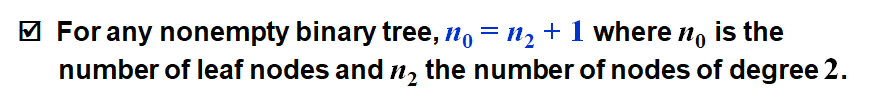树 | Tree

OI-Wiki Tree Basic

相关定义

树叶（leaf）：没有儿子的节点。
兄弟（sibling）：有相同父亲的节点。
到路径长（length）：边的条数。
的深度（depth）：根到的路径长。
的高度（height）：从到一片树叶的最长路径长。

树的实现

FirstChild-NextSibling Representation

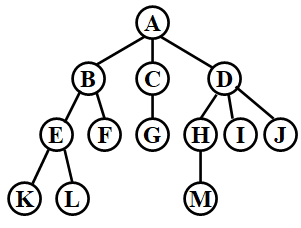
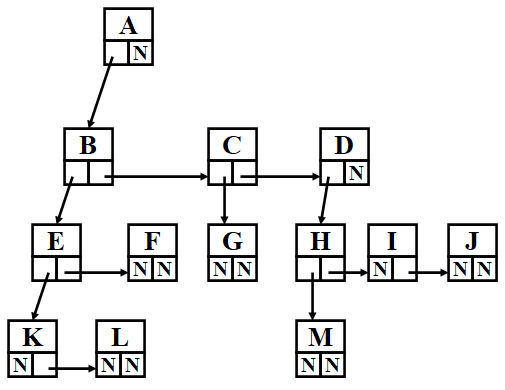
这种表示方法不唯一，因为没有规定children的顺序。

二叉树 | Binary Tree

树的遍历 | Tree Traversals

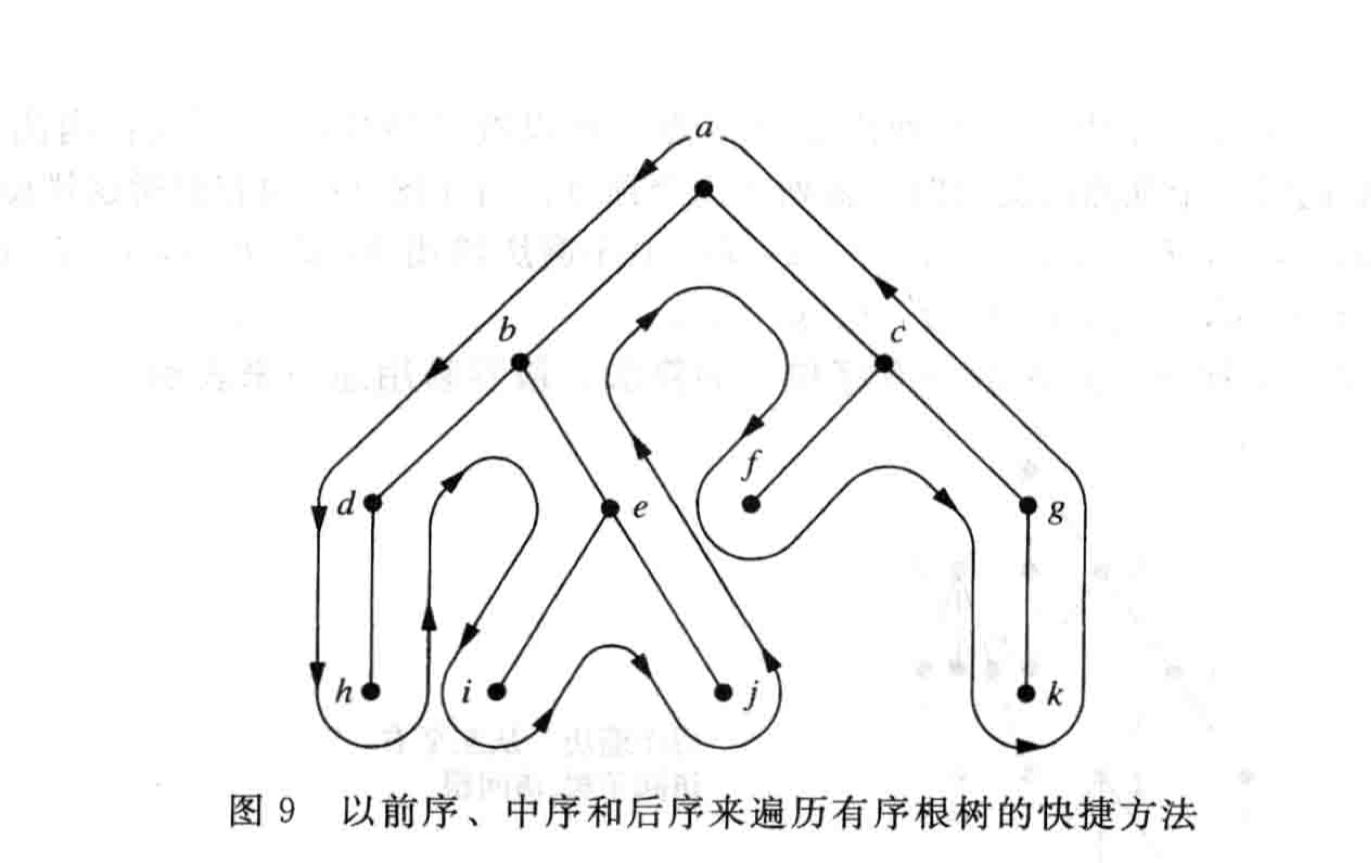
先、中、后序遍历

层次遍历

用到了队列数据结构。每次出队一个节点，就把它的所有孩子加入队列。伪码如下：

void  levelorder ( tree_ptr  tree ){   enqueue ( tree );
    while (queue is not empty) {
        visit ( T = dequeue ( ) );
        for (each child C of T )
            enqueue ( C );
    }
}

具体实现（同时可以知道现在遍历到哪个层次）

void levelOrder(struct tree *BT){
    int level = 1;
    struct *queue[MEM], **front = queue, **rear = queue;
    struct tree * curNode = BT;
    //enqueue
    if(BT != NULL){
        *rear = BT;
        rear++;
        *rear = NULL
        rear++;      //把NULL作为分隔标志，借此确定层次
    }
    while(front != rear){
        curNode = *front;
        front++;      //dequeue
        if (curNode == NULL) {  //遇到NULL分隔符，说明确实遍历了一个层次
            if (front == rear) break;
            level++;
            *rear = NULL;  //
            rear++;
            continue;       
        }
        if (curNode->left != NULL) {
            *rear = curNode->left;
            rear++;
        }
        if (curNode->right != NULL) {
            *rear = curNode->right;
            rear++;
        }
    }
}

用栈实现前、中、后序遍历（None Recursive Way）

利用栈的FILO特性和三种遍历的特点。

#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
#define INF -9223372036854775808
struct tree {
    int data;
    struct tree *left, *right;
}*binTree;
struct tree*createTree(int in[],int pre[],int n) { 
    if (n == 0) return NULL;
    struct tree *root = (struct tree *) malloc(sizeof(struct tree));
    root->data = pre[0];
    int n1 = 0, n2 = 0, here = 0,
            lIn[MAXN] = {0}, rIn[MAXN] = {0}, lPre[MAXN] = {0}, rPre[MAXN] = {0};
    while (in[here] != pre[0]) here++;
    for (int i = 0; i < here; i++) lIn[n1++] = in[i];
    for (int i = here + 1; i < n; i++) rIn[n2++] = in[i];
    for (int i = 0; i < n1; i++) lPre[i] = pre[i + 1];
    for (int i = 0; i < n2; i++) rPre[i] = pre[n1 + i + 1];
    root->left = createTree(lIn, lPre, n1);
    root->right = createTree(rIn, rPre, n2);
    return root;
}
/*入栈一个节点就出栈并访问其值，遇到空时弹出当前栈顶节点并访问其右子树，重复之前操作*/
void stackPreOrder(struct tree*root) {
    int stack1[MAXN] = {0}, s1Bottom = INF, *sp1 = &s1Bottom; //actually do not need stack1 now
    struct tree **stack2[MAXN], *s2Bottom = NULL, **sp2 = &s2Bottom;
    while (root != NULL || sp2 != &s2Bottom) {
        if (root) {
            *(++sp1) = root->data;
            *(++sp2) = root; //push
            printf("%d ", root->data);
            root = root->left;
        } else {
            root = *(sp2--);
            root = root->right;
        }
    }
}
/*一直访问左子树直至遇到空，弹出栈顶节点，访问其值，并访问其右子树*/
void stackInOrder(struct tree*root) {
    int stack1[MAXN] = {0}, s1Bottom = INF, *sp1 = &s1Bottom; //actually do not need stack1 now
    struct tree **stack2[MAXN], *s2Bottom = NULL, **sp2 = &s2Bottom;
    while (root != NULL || sp2 != &s2Bottom) {
        if (root) {
            *(++sp2) = root;
            root = root->left;
        } else {
            root = *(sp2--);
            printf("%d ",root->data);
            root = root->right;
        }
    }
}
void stackPostOrder(struct tree*root) {
    int stack1[MAXN] = {0}, s1Bottom = INF, *sp1 = &s1Bottom;
    struct tree **stack2[MAXN], *s2Bottom = NULL, **sp2 = &s2Bottom;
    while (root != NULL || sp2 != &s2Bottom) {
        if (root) {
            *(++sp1) = root->data;
            *(++sp2) = root;
            root = root->right;
        } else {
            root = *(sp2--);
            root = root->left;
        }
    }
    while (sp1 != &s1Bottom)
        printf("%d ", *(sp1--));
}
int main() {
    int n, in[MAXN], pre[MAXN];
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &in[i]);
    for (int i = 0; i < n; i++) scanf("%d", &pre[i]);
    binTree = createTree(in, pre, n);
    printf("preorder:\n");
    stackPreOrder(binTree);
    printf("\ninorder:\n");
    stackInOrder(binTree);
    printf("\npostorder:\n");
    stackPostOrder(binTree);
}

树的建立

根据中序和后（前）序建立树

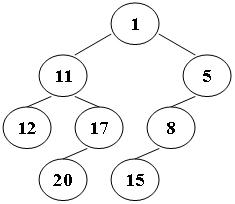
用这个树举个例子，inorder：12->11->20->17->1->15->8->5，postorder：12->20->17->15->8->5->1。
可以注意到postorder的特点是根节点总在最后一个被访问，据此可以把inorder分为左子树和右子树，进行完这个过程后，可以把postorder再分为左子树和右子树，至此，可以进行递归。如此操作直到左子树没有元素后到达递归出口。
如果后序改为前序，则根节点总在第一个被访问，其余相同。

struct tree* createTree(int inSeq[], int postSeq[], int items) {
    if (items == 0) {
        return NULL;
    }   //没有元素，开始返回
    struct tree* root = (struct tree*)malloc(sizeof(struct tree));
    int lInSeq[MEM], rInSeq[MEM], lPostSeq[MEM], rPostSeq[MEM];
    root->key = postSeq[items - 1];
    //将inorder分为左子树和右子树
    int lItems = 0, rItems = 0;    
    for (int i = 0; i < items; i++) {
        if (i <= lItems && inSeq[i] != postSeq[items - 1]) {
            lInSeq[lItems] = inSeq[i];
            lItems++;
        }
        if (i > lItems) {
            rInSeq[rItems] = inSeq[i];
            rItems++;
        }
    }
    //将postorder分为左子树和右子树
    for (int i = 0; i < lItems; i++) lPostSeq[i] = postSeq[i];
    for (int i = lItems; i < items - 1; i++) rPostSeq[i - lItems] = postSeq[i];
    root->left = createTree(lInSeq, lPostSeq, lItems);
    root->right = createTree(rInSeq, rPostSeq, rItems);
    return root;
}

树的性质

一些树

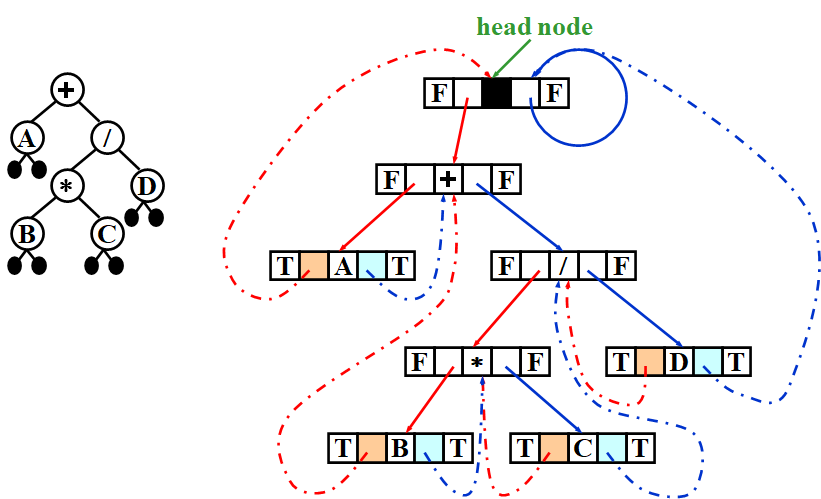
Threaded Binary Trees

一个满二叉树，n个顶点，有n-1条边，n+1个NULL边，浪费很大。
这里的规则建立起了inorder的Threaded Binary Trees。

• Rule 1: If Tree->Left is NULL, replace it with a pointer to the inorder predecessor（前辈） of Tree.
• Rule 2: If Tree->Right is NULL, replace it with a pointer to the inorder successor（后继者） of Tree.

• Rule 3: There must not be any loose threads. Therefore a threaded binary tree must have a head node of which the left child points to the first node.

  typedef  struct  ThreadedTreeNode  *PtrTo  ThreadedNode;
  typedef  struct  PtrToThreadedNode  ThreadedTree;
  typedef  struct  ThreadedTreeNode {
       int                   LeftThread;   /* if it is TRUE, then Left */
       ThreadedTree      Left;      /* is a thread, not a child ptr.   */
       ElementType    Element;
       int                   RightThread; /* if it is TRUE, then Right */
       ThreadedTree      Right;    /* is a thread, not a child ptr.   */
  }

  

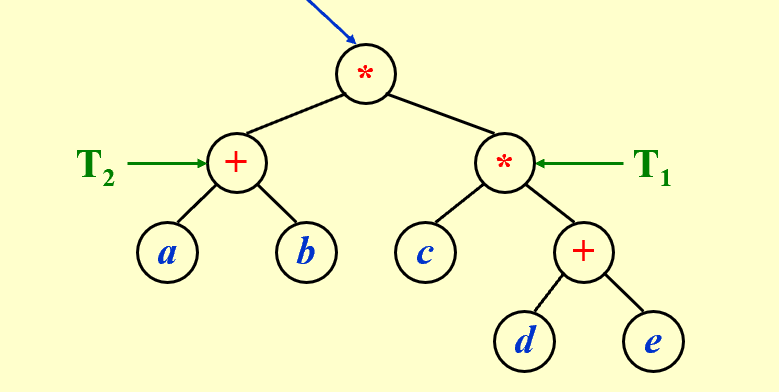
  语法树 | Syntax Tree

  后序遍历：
  

  二叉搜索树 | Binary Search Tree

  定义

• 每个节点都有一个值为整数的key，且互不相同。

• 对于一个顶点，其左子树的所有key小于顶点的key，右子树的key大于顶点的key。
• 左右子树也是二叉搜索树。

• 可以为空。

  操作

  Insert
  先检查要插入的元素是否在树中，若不在，再执行插入。
  伪码如下：

  SearchTree  Insert( ElementType X, SearchTree T ) { 
    if ( T == NULL ) { /* Create and return a one-node tree */ 
    T = malloc( sizeof( struct TreeNode ) ); 
    if ( T == NULL ) 
       FatalError( "Out of space!!!" ); 
    else { 
       T->Element = X; 
       T->Left = T->Right = NULL; } 
      }  /* End creating a one-node tree */
    else  /* If there is a tree */
     if ( X < T->Element ) 
       T->Left = Insert( X, T->Left ); 
    else 
        if ( X > T->Element ) T->Right = Insert( X, T->Right ); 
       /* Else X is in the tree already; we'll do nothing */ 
    return  T;   /* Do not forget this line!! */ 
  }

  Delete

• 删除叶节点：将其parent指向null。

• 删除度为1的节点：用它的孩子代替它。
• 删除度为2的节点：用其左子树中最大的元素或右子树中最小的元素代替它，再把这个元素从树中删除。这样做的目的是降低树的高度，尽量达到Complete Binary Tree。

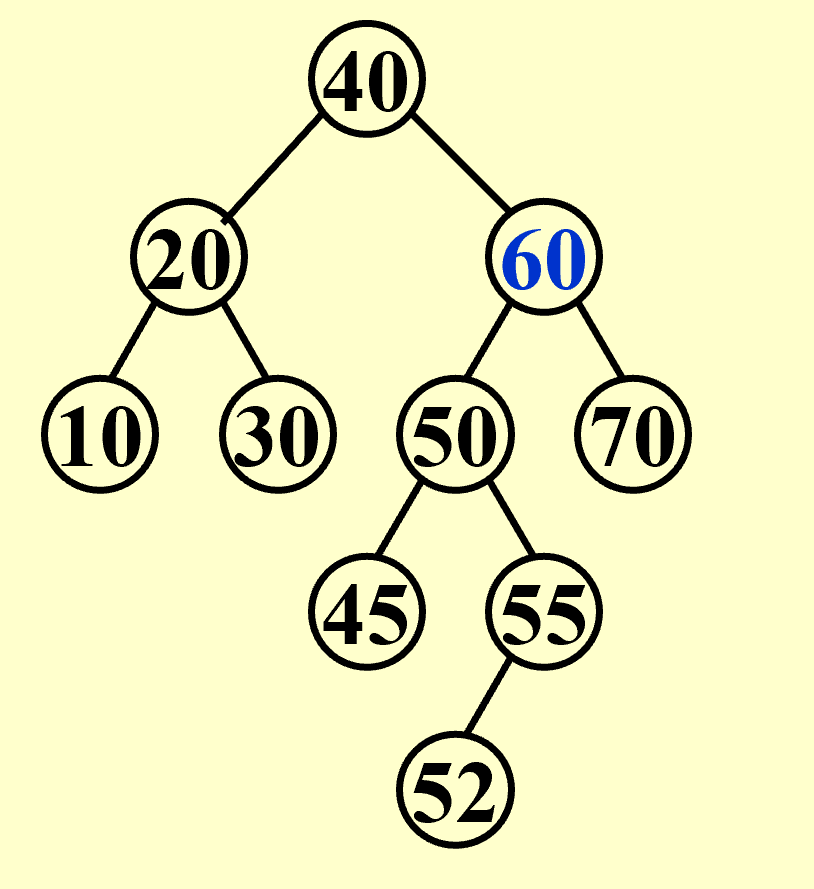
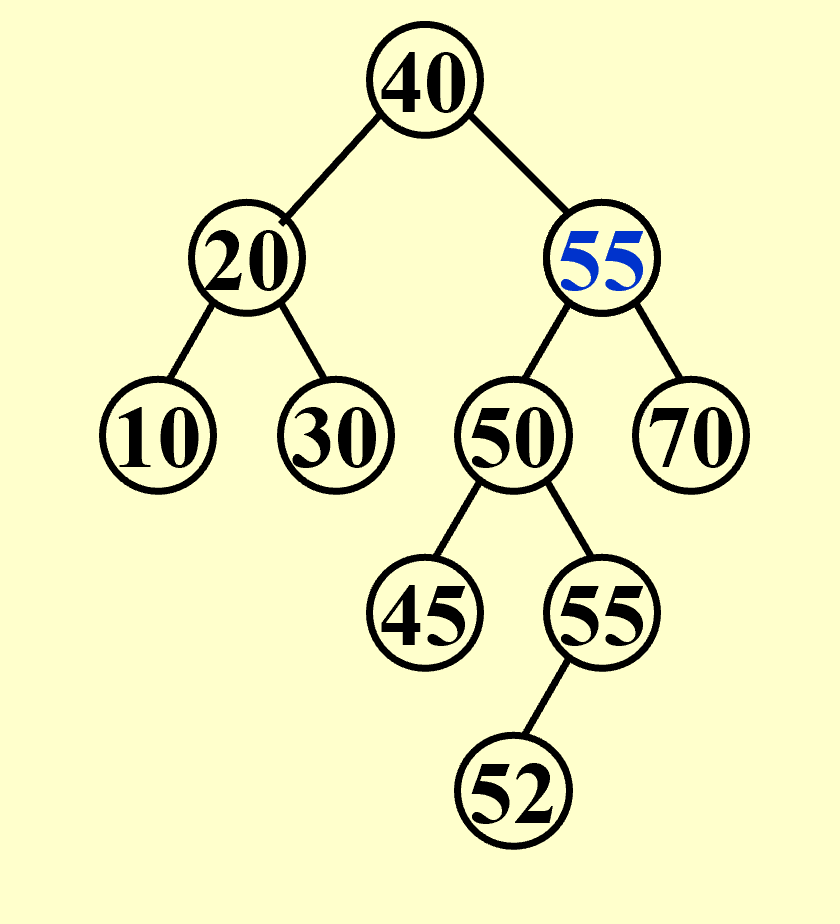
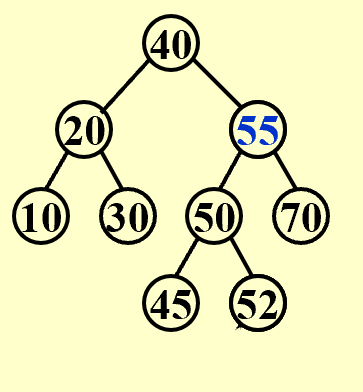
SearchTree  Delete( ElementType X, SearchTree T ) 
{    Position  TmpCell; 
      if ( T == NULL )   Error( "Element not found" ); 
      else  if ( X < T->Element )  /* Go left */ 
        T->Left = Delete( X, T->Left ); 
               else  if ( X > T->Element )  /* Go right */ 
               T->Right = Delete( X, T->Right ); 
             else  /* Found element to be deleted */ 
               if ( T->Left && T->Right ) {  /* Two children */ 
                   /* Replace with smallest in right subtree */ 
                   TmpCell = FindMin( T->Right ); 
                   T->Element = TmpCell->Element; 
                   T->Right = Delete( T->Element, T->Right );  } /* End if */
               else {  /* One or zero child */ 
                   TmpCell = T; 
                   if ( T->Left == NULL ) /* Also handles 0 child */ 
                 T = T->Right; 
                   else  if ( T->Right == NULL )  T = T->Left; 
                   free( TmpCell );  }  /* End else 1 or 0 child */
      return  T; 
}

Implementation of BST-ADT

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MEM 100
struct tree{
    int data;
    struct tree*left,*right;
}*BST;
int arr[MEM],n;
struct tree*find(int X,struct tree*root) {
    if (root == NULL) return NULL;
    if (X < root->data) return find(X, root->left);
    else if (X > root->data) return find(X, root->right);
    else return root;
}
struct tree*findMin(struct tree*root){
    if(!root) return NULL;
    else{
        if(root->left==NULL) return root;
        else return findMin(root->left);
    }
}
struct tree*findMax(struct tree*root){
    if(!root) return NULL;
    else{
        if(root->right==NULL) return root;
        else return findMin(root->right);
    }
}
struct tree*insert(int X,struct tree*root) {
    if (root==NULL) {
        root=(struct tree*) malloc(sizeof (struct tree));
        root->data=X;
        root->left=root->right=NULL;
    }
    else{
        if(root->data>X) root->left=insert(X,root->left);
        else if(root->data<X) root->right=insert(X,root->right);
        else ; //do nothing when X is already in tree
    }
    return root;
}
struct tree*delete(int X,struct tree*root){
    struct tree* tmp;
    if(root==NULL) {
        printf("No this element");
        exit(0);
    }
    else if(X< root->data) root->left= delete(X,root->left);
    else if(X> root->data) root->right= delete(X,root->right);
    else{
        if(root->left&&root->right){ //has two children
            tmp= findMax(root->left); //or findMin(root->right)
            root->data=tmp->data; //rewrite instead of swap
            root->left= delete(root->data,root->left); //delete tmp
        }
        else { //no child or one
            tmp=root;
            if(root->left==NULL) root=root->right;
            else if(root->right==NULL) root=root->left;
            free(tmp);
        }
    }
    return root;
}
void inOrder(struct tree *root){
    if(root){
        inOrder(root->left);
        printf("%d ",root->data);
        inOrder(root->right);
    }
}
int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d", &arr[i]);
        BST= insert(arr[i],BST);
    }
    inOrder(BST);
    printf("\n");
    srand(time(0));
    BST=delete(arr[rand()%n],BST);
    inOrder(BST);
    return 0;
}

结合一定条件建立一个完全二叉搜索树

给定一个整数序列，建立完全二叉搜索树（是唯一的）。

• 将序列按升序排列，也即给出了中序序列，便于后续分割。
• 找到根节点（可以由完全二叉树性质推得），将树分为左右子树，对左右子树做相同操作。

这里排序我结合了一下后面堆 | Heap的知识，用了小顶堆排序。这里可以看到用数组存树是很方便的。

#pragma warning(disable:4996) 
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#define MEM 10000
#define MIN -1
int n, arr[MEM], heapSize;
int sortedArr[MEM], CBT[MEM];
int leftSubElements(int nodes) {
    int height = (int)(log(nodes + 1) / log(2)); //get height
    int leaves = nodes - (int)pow(2, height) + 1; //number of leaf nodes
    int half = pow(2, height-1); //half nmber of leaf nodes
    int leftLeaves = (leaves < half) ? leaves : half;
    return (int)pow(2, height - 1) - 1 + leftLeaves;
}
void percolateDown(int pos) {
    int X = arr[pos], i, child;
    for (i = pos; i * 2 <= heapSize; i = child) {
        child = i * 2;
        if (child != heapSize && arr[child + 1] < arr[child]) child++;
        if (arr[child] < X) arr[i] = arr[child];
        else break;
    }
    arr[i] = X;
}
void createMinHeap() {
    for (int i = heapSize / 2; i >= 1; i--) {
        percolateDown(i);
    }
}
void delete() {
    if (heapSize == 0) return;
    int min = arr[1];
    int last = arr[heapSize--];
    arr[1] = last;
    percolateDown(1);
}
void minHeapSort() {
    for (int i = 1; heapSize != 0; i++) {
        sortedArr[i - 1] = arr[1];
        delete();
    }
}
void createTree(int left, int right, int root) {
    int nodes = right - left + 1;
    if (nodes == 0) return;
    int leftNodes = leftSubElements(nodes);
    CBT[root] = sortedArr[left + leftNodes];
    createTree(left, left + leftNodes - 1, 2 * root + 1);
    createTree(left + leftNodes + 1, right, 2 * root + 1 + 1);
}
int main() {
    scanf("%d", &n);
    heapSize = n;
    arr[0] = MIN;
    for (int i = 0; i < n; i++) scanf("%d", &arr[i + 1]);
    createMinHeap();
    minHeapSort();
    createTree(0, n - 1, 0);
    for (int i = 0; i < n; i++) {
        if (i == 0) printf("%d", CBT[i]);
        else printf(" %d", CBT[i]);
    }
    return 0;
}