Delete（这里理解为执行）the element with the highest / lowest priority.

二叉堆 | Binary Heap

性质

二叉堆的简单实现使用数组。首先先回顾完全二叉树，如下图。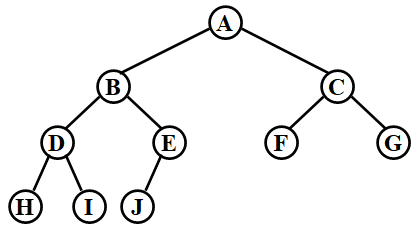
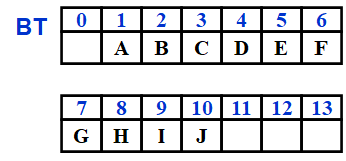
image.pngimage.png
有n个节点的完全二叉树用数组以层序储存，下标为i(1<=i<=n)的节点有如下性质。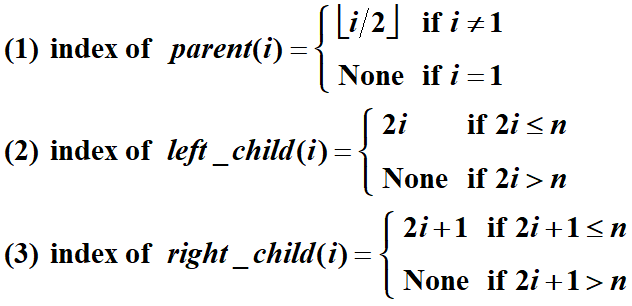
image.png

堆序 | Heap Order

min tree：节点的值总不大于其children的值。
max tree：节点的值总不小于其children的值。

基本操作

这里均以min tree为例

Insert

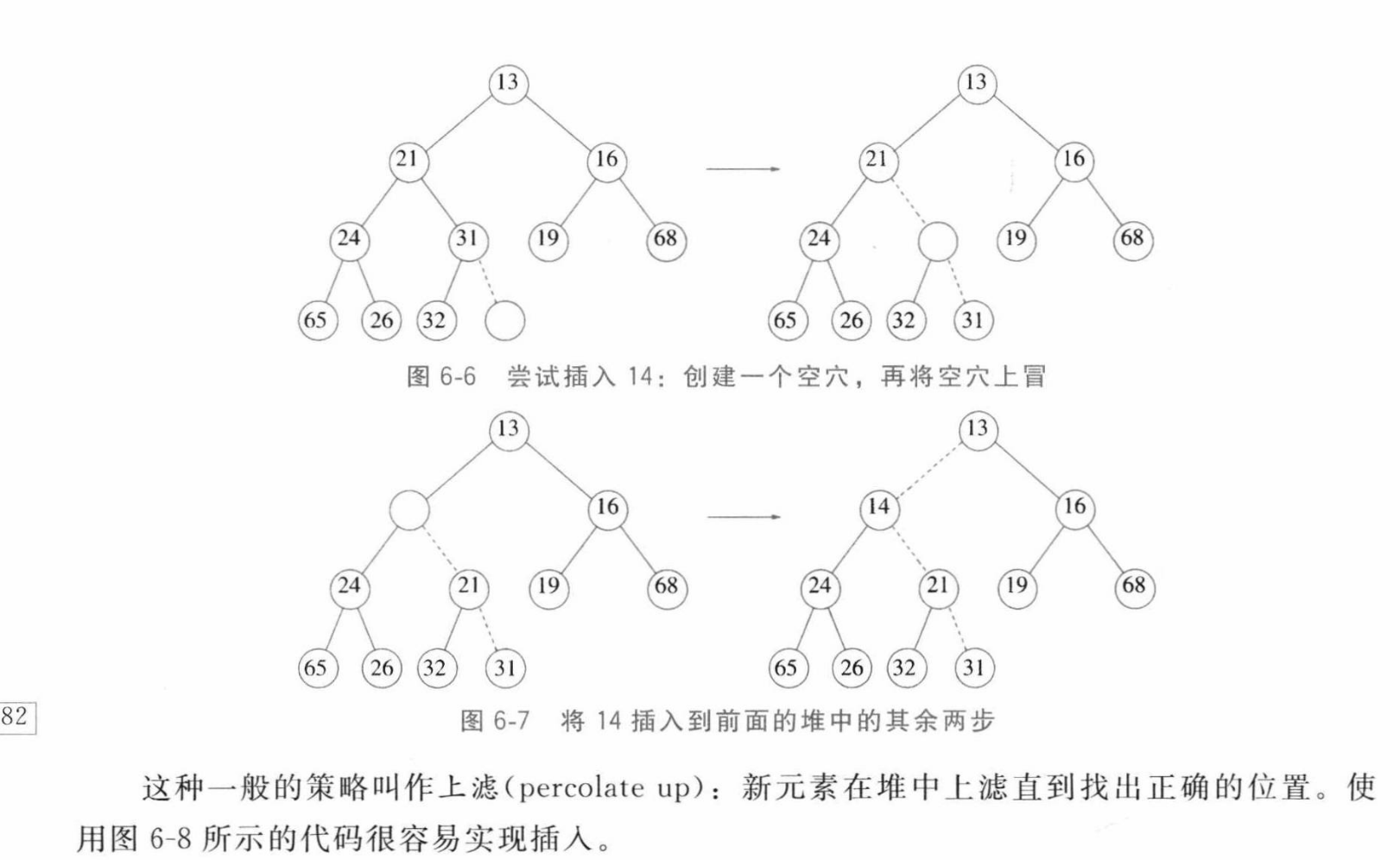
image.png

  1. /* H->Element[ 0 ] is a sentinel */ 
  2. void  Insert( ElementType  X,  PriorityQueue  H ) 
  3. { 
  4.      int  i; 
  5.     if ( IsFull( H ) ) { 
  6.         Error( "Priority queue is full" ); 
  7.     return; 
  8.     }
  9.     //percolate up
  10.     for ( i = ++H->Size; H->Elements[ i / 2 ] > X; i /= 2 ) 
  11.         H->Elements[ i ] = H->Elements[ i / 2 ]; 
  13.      H->Elements[ i ] = X; 
  14. }

如果是max tree，for循环判断条件改为<即可。

Delete

删除最小元素后，将队尾的元素移到root处，再下滤至符合要求。

  1. ElementType  DeleteMin( PriorityQueue  H ) 
  2. { 
  3.     int  i, Child; 
  4.     ElementType  MinElement, LastElement; 
  5.     if ( IsEmpty( H ) ) { 
  6.          Error( "Priority queue is empty" ); 
  7.          return  H->Elements[ 0 ];   } 
  8.     MinElement = H->Elements[ 1 ];  /* save the min element */
  9.     LastElement = H->Elements[ H->Size-- ];  /* take last and reset size */
  10.     for ( i = 1; i * 2 <= H->Size; i = Child ) {  /* Find smaller child */ 
  11.          Child = i * 2; 
  12.          if (Child != H->Size && H->Elements[Child+1] < H->Elements[Child]) 
  13.            Child++;     
  14.          if ( LastElement > H->Elements[ Child ] )   /* Percolate one level */ 
  15.            H->Elements[ i ] = H->Elements[ Child ]; 
  16.          else     break;   /* find the proper position */
  17.     } 
  18.     H->Elements[ i ] = LastElement; 
  19.     return  MinElement; 
  20. }

BulidHeap

对一个未成堆的序列，采用下滤的方式使其成堆（min tree）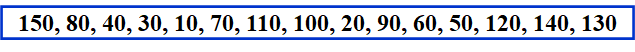
image.png
只需percolate down(7), percolate down(6), percolate down(5), percolate down(4), percolate down(3), percolate down(2), percolate down(1)，传入的参数为数组下标。一般地，从堆 | Heap - 图6开始下滤。
For the perfect binary tree of height h containing堆 | Heap - 图7nodes, 除去最后一层堆 | Heap - 图8个点, the sum of the heights of the nodes is 堆 | Heap - 图9，时间复杂度为O(n)。

堆排序

堆排序的基本思想是：将待排序序列构造成一个小顶堆（min tree），此时，整个序列的最小值就是堆顶的根节点。然后执行Delete操作。再将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序升序列了，反之max tree可以构造降序列。时间复杂度近似为O(nlogn）。

  1. void percolateDown(int pos) {
  2.     int X = arr[pos], i, child;
  3.     for (i = pos; i * 2 <= heapSize; i = child) {
  4.         child = i * 2;
  5.         if (child != heapSize && arr[child + 1] < arr[child]) child++;
  6.         if (arr[child] < X) arr[i] = arr[child];
  7.         else break;
  8.     }
  9.     arr[i] = X;
  10. }
  13. void createMinHeap() {
  14.     for (int i = heapSize / 2; i >= 1; i--) {
  15.         percolateDown(i);
  16.     }
  17. }
  19. void delete() {
  20.     if (heapSize == 0) return;
  21.     int min = arr[1];
  22.     int last = arr[heapSize--];
  23.     arr[1] = last;
  24.     percolateDown(1);
  25. }
  27. void minHeapSort() {
  28.     for (int i = 1; heapSize != 0; i++) {
  29.         sortedArr[i - 1] = arr[1];
  30.         delete();
  31.     }
  32. }

d-Heap

对于下标为i的项，其children所在的下标为堆 | Heap - 图10，其parent所在的下标为堆 | Heap - 图11