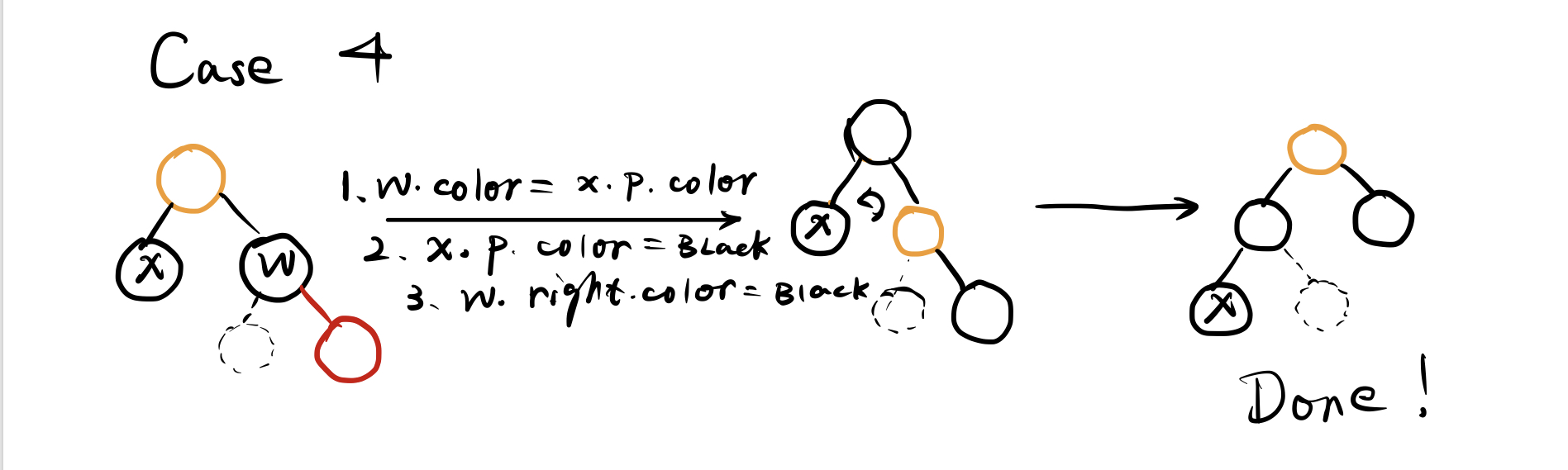Red-Black Trees

• 每个节点要么红要么黑
• 根节点是黑色
• 叶节点( NIL )是黑色，但不显式的画出（红黑树中的叶节点是NULL指针）
• 红节点的两个儿子必须是黑色
• 对于每个节点，从其出发到叶节点的所有简单路径都有相同个数的黑节点

定义：黑高( black-height )，bh(x)，是从x出发到叶子的简单路径上黑点的个数。 :::info :::

Insert

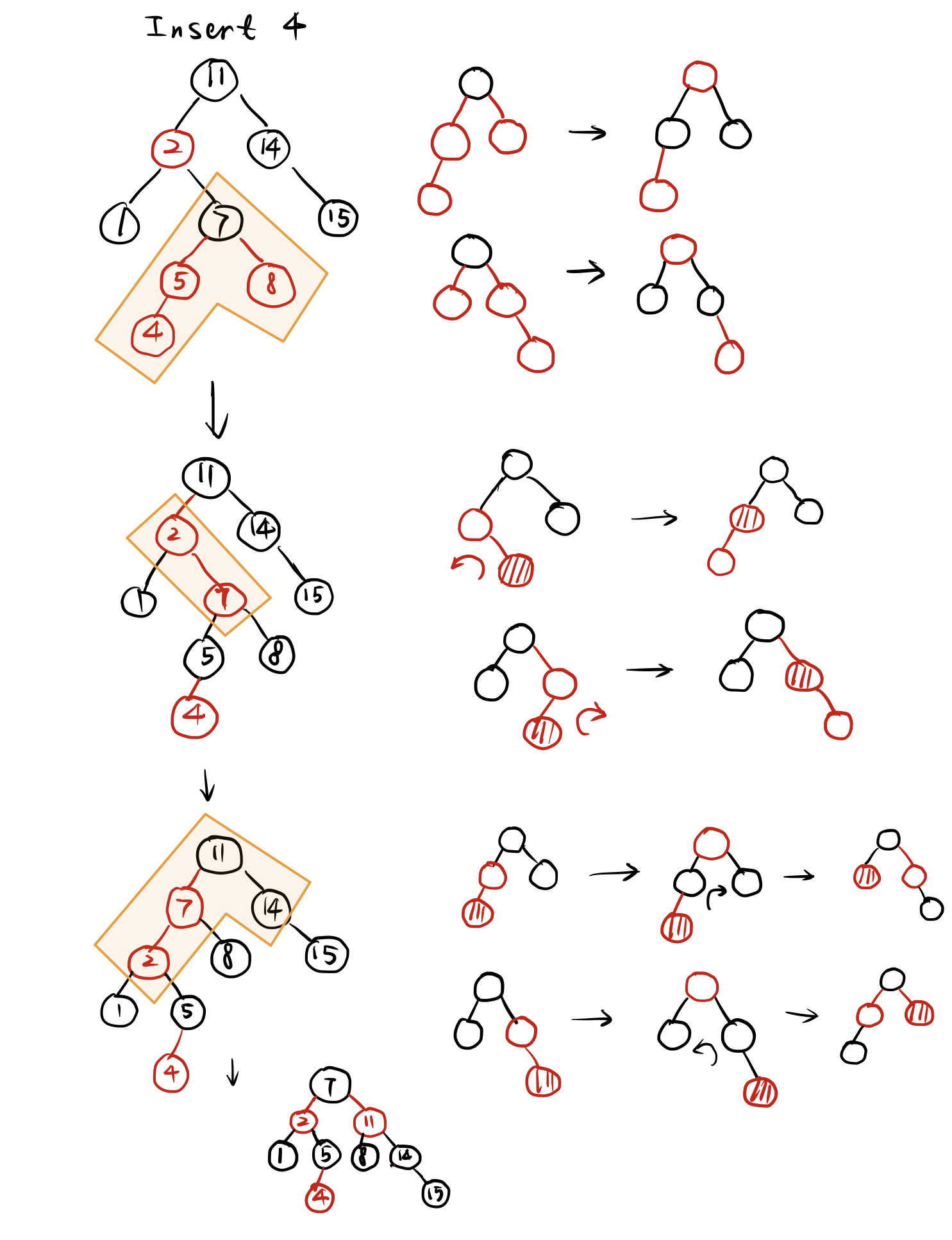
上图由上到下依次编号情况为1 2.2 2.1 ，那么我们有如下FSM：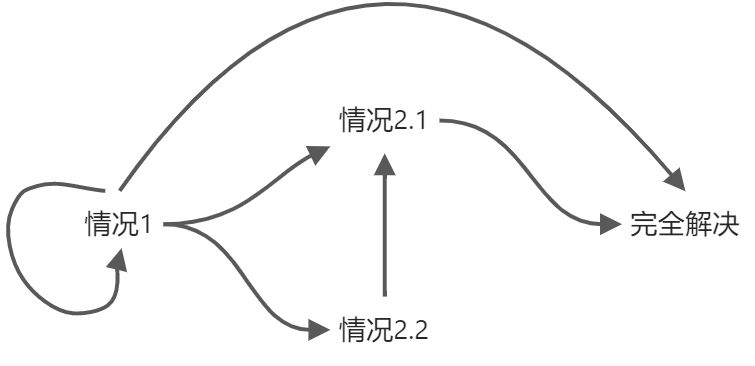

Delete

重量级……看了好久才学会
https://www.bilibili.com/video/BV1uZ4y1P7rr?spm_id_from=333.337.search-card.all.click
看这个才搞明白什么是x，红黑树的删除分为以下两个部分：

1. 普通二叉搜索树意义上的删除，需要记住哪个节点（即x）去替代了被删除节点

• 删除叶子节点
  • 如果是红，直接将parent置为NIL
  • 如果是黑，需要判断
• 删除度为1的节点：用其孩子替代
• 删除度为2的节点
  • 用左子树中最大或右子树中最小替代
  • 将子树中的这个点删掉

1. 通过调整使得树的结构满足红黑树的定义，这里有五个case

• Case0：
  • 把 x 涂成黑色
• Case1
  • 
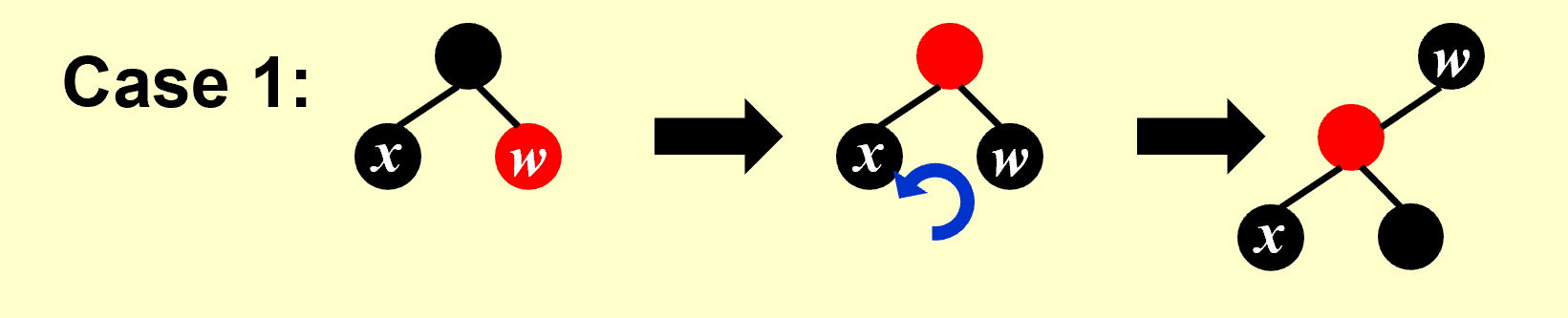
  • 依据转出的结果来确定转到Case2, 3, 4的哪种
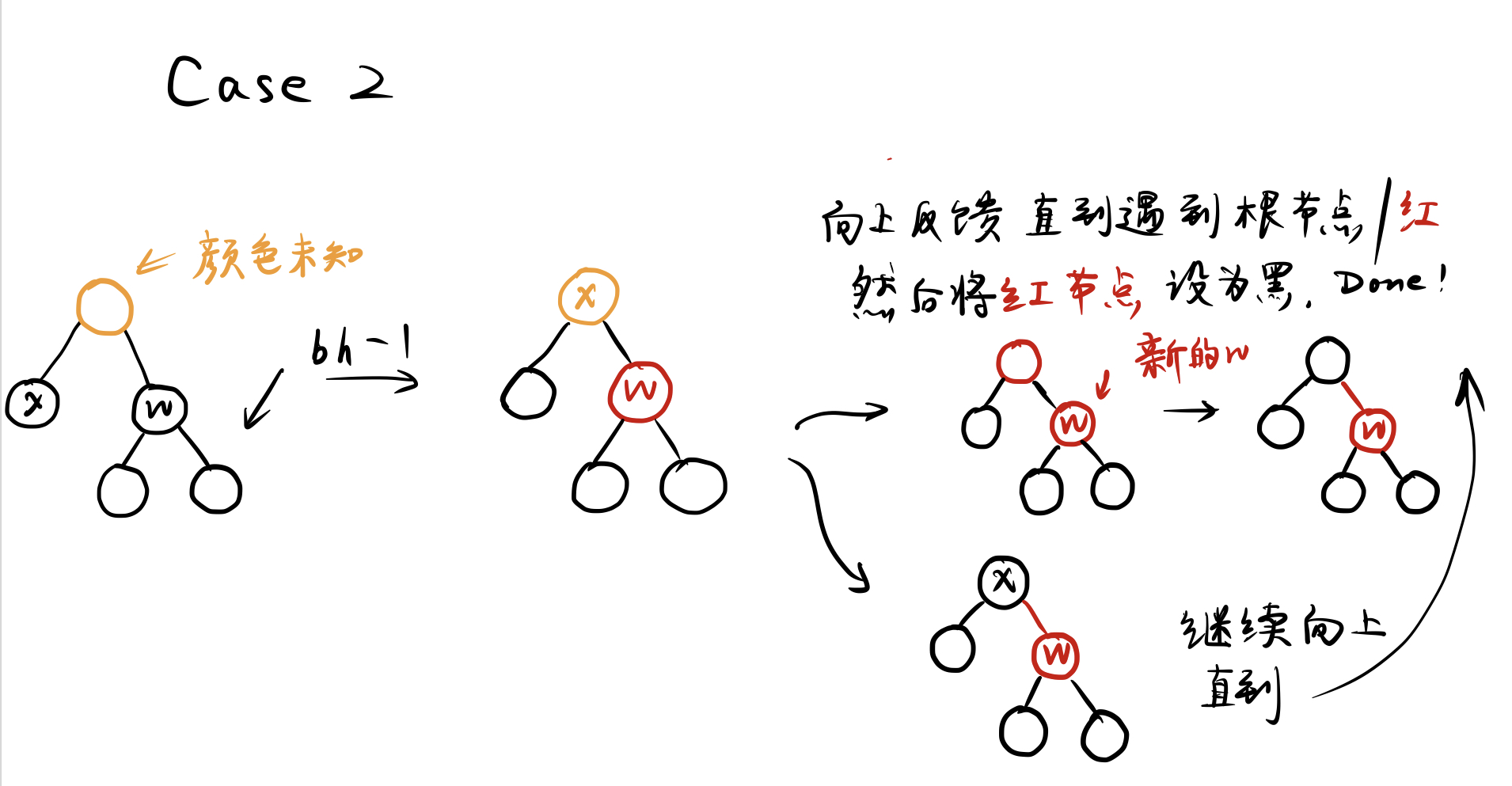
• Case2
  • 
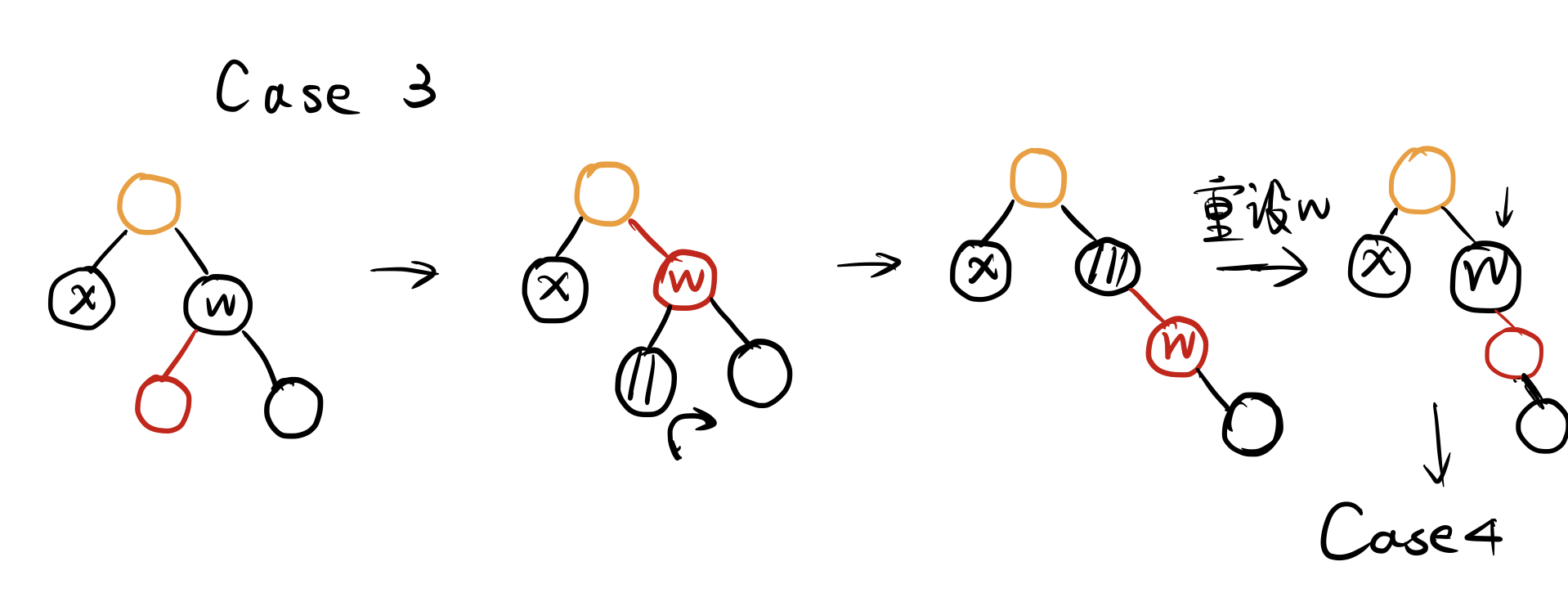
• Case3
  • 
• Case4
  • 

其实所有的调整都是基于删除黑节点后一边子树黑高发生变化，然后要使两边黑高重新平衡来调整的。下面是一个例子：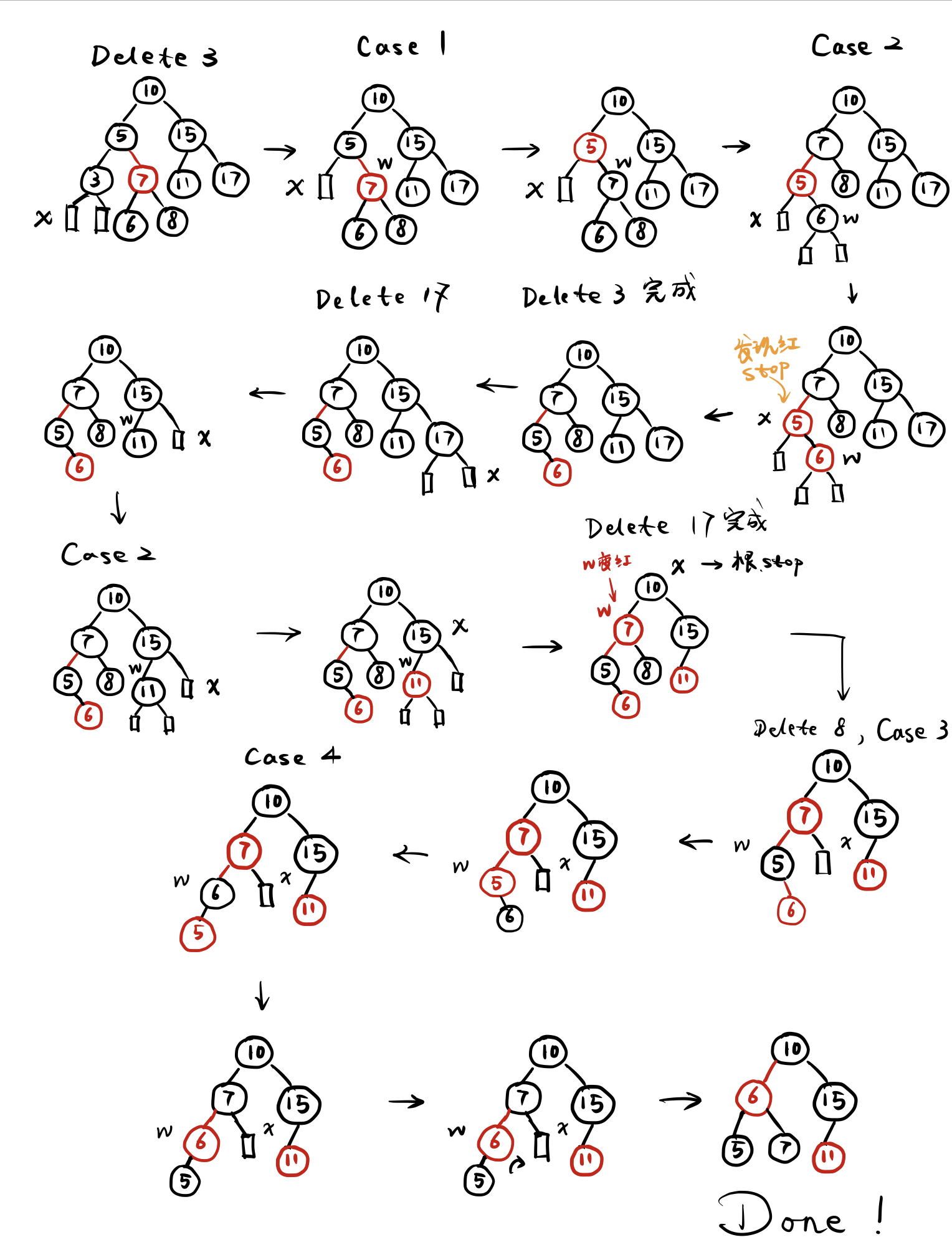

B+ Trees

Insert

课上讲的B+树分裂时的条件不太一样，对于叶子节点是最多可以存M个key，到M+1时就分裂，内节点是最多M-1个key，到M个时就分裂。

Delete

这个也是重量级，目前代码还不会

• https://www.programiz.com/dsa/deletion-from-a-b-plus-tree