Leftis Heap

引入左式堆的原因在于我们想要加速堆的合并。对于经典的堆，合并的方式有两种，第一种是堆的规模较小时，直接拷贝到新的堆，复杂度为，第二种是堆的规模较大时，我们设，将较小的堆插入到较大堆中，时间复杂度为。

定义

左式堆仍具有堆的性质，但不是完全二叉树了。 :::info

• 零路径长 | Null Path Length
• 对于任意一个节点 X，Npl( X ) 定义为从 X 开始的到达没有两个孩子的节点的最短路径长，其中Npl( null ) = -1
• ，C 是 X 的所有孩子 ::: 对于每一个顶点，其左儿子的Npl值不小于其右儿子的Npl值，具有这样性质的堆是左式堆。

  性质

  
  从上面性质得到的一个推论是右路径的长不多于，这保证了我们合并时的效率。

  Merge

  Recursive Way

  合并的递归描述如下：

1. 如果有一个堆为空，返回非空堆
2. 比较两个堆的堆顶元素的大小，以较小的作为新堆的根，将较小堆的右子树和较大堆合并
3. 如有必要，交换左右子树使得满足左式堆的定义
4. 更新节点Npl值

5. 递归进行上述过程

   PriorityQueue Merge( PriorityQueue H1, PriorityQueue H2 )
   { 
    if (H1==NULL) return H2;
    if (H2==NULL) return H1;
    if (H1->Element > H2->Element)
        Swap(H1, H2);  
    if ( H1->Left == NULL ) H1->Left = H2;  //左树为空，为满足Npl定义，插入到左树           
    else {
        H1->Right = Merge( H1->Right, H2 );
        if ( H1->Left->Npl < H1->Right->Npl ){
            SwapChildren( H1 );  //满足Npl，交换左右子树
        }
        H1->Npl = H1->Right->Npl + 1;
    }
    return H1;
   }

   Iterative Way

   https://www.uio.no/studier/emner/matnat/ifi/INF4130/h17/losningsforslag/losningsforslag-ukeoppgave8.pdf Exercise4

Merge 操作的时间复杂度是，基于右路径长的性质。

Delete & Insert

Delete 和 Insert 完全基于 Merge ，Delete 堆顶元素后，合并左右子树，Insert可以看做大小为1的堆和原堆的合并。此处不再赘述。这两个操作的时间复杂度也是。

Skew Heap

斜堆和左式堆的关系类似于伸展树和 AVL 树，斜堆的核心想法也是在连续 M 次操作下，合并花费的摊还时间不超过。递归例程中的唯一区别是每次不加判断的进行左右儿子的交换，而这样带来的后果是最终产生的堆可能很不符合左式堆的定义，right path 的长度可能任意长。

斜堆的摊还分析

注意这里 heavy 和 light 的定义

• heavy 定义为节点 p 的右子树的节点个数至少是节点 p 后继节点总数的一半
• light 相反定义

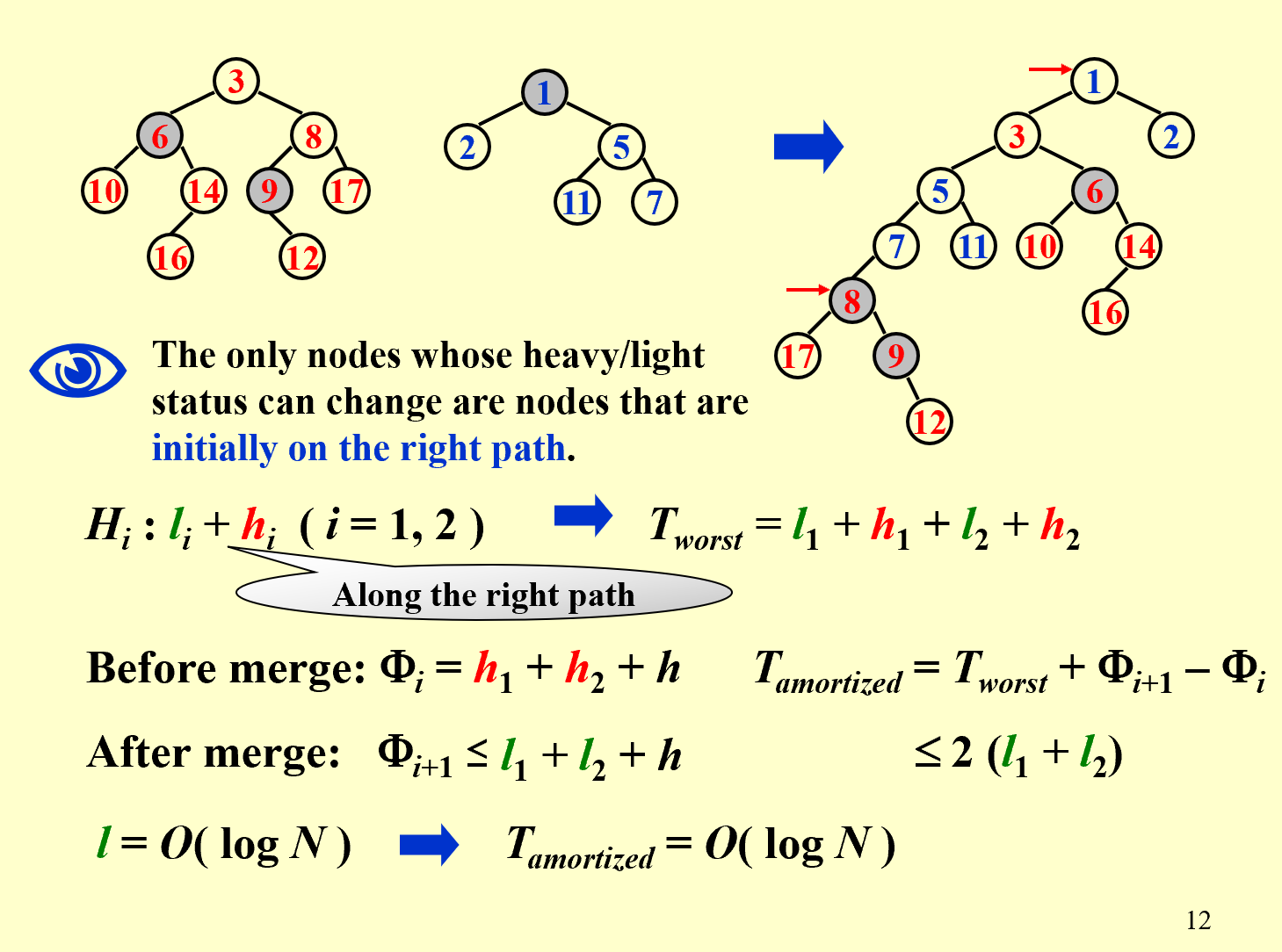
推出 light 节点的个数的界是，也即摊还时间复杂度。