数据结构基础 | FDS - 图 | Graph - 《Something》

AOE network
图的匹配
- 一些概念
- 二分图匹配
网络最大流
DFS的应用

讨论不包括多重图，没有loop

AOE network

图的匹配

参考这里

一些概念

在中，边集,中的任意两条边都不依附于同一个顶点，则称是一个匹配。
最大时称为最大匹配，当图中的边带权的时候，边权和最大的为最大权匹配。
匹配中的边称为匹配边，反之称为未匹配边。
一个点如果属于且为至多一条边的端点，称为匹配点，反之称为未匹配点。
最大匹配（maximum matching): 匹配数最多的匹配。
完美匹配（perfect matching): 所有点都属于匹配，同时也符合最大匹配。
二分图匹配
二分图较为特殊，完美匹配：，为的最大匹配，若，则为完美匹配。
霍尔定理 | Hall

这里有例题

二分图最大匹配（undone）

二分图最大权匹配（undone）

网络最大流

EK算法 | Edmonds-Karp

每次寻找增长通路时是用无权最短路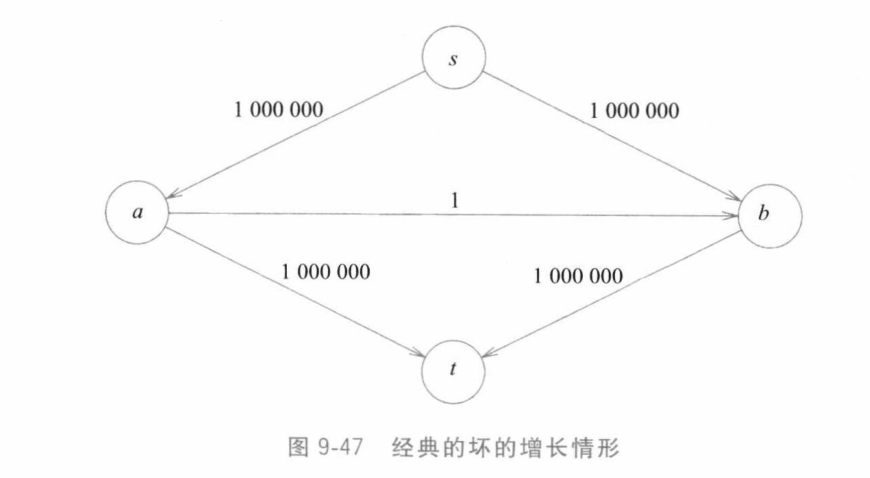算法，即BFS，复杂度为图 | Graph - 图19 ，考虑最大流为图 | Graph - 图20 ，则复杂度为图 | Graph - 图21 ，坏的例子如下：

Dicnic算法（未完成）

最大流和最小割的关系

最大流等于最小割

割的定义：将一个图分割成不连通的两个子图。
最小割，称为图 | Graph - 图22 割，满足：

图 | Graph - 图26 割的容量是指为了割开而形成两个子图需要删掉的边的容量之和，只统计从 图 | Graph - 图27 到图 | Graph - 图28 的边的容量之和。最小割即希望这个值尽量小。

DFS的应用

DFS求连通分支

void DFS(struct GNode*p,int vertex) {
    visit[vertex] = 1;
    printf("%d ", vertex);
    for (int i = 1; i <= p->V; i++) {
        if (p->G[vertex][i] && !visit[i]) {
            DFS(p, i);
        }
    }
}
void FindComponents(struct GNode*p) {
    for (int i = 1; i <= p->V; i++) {
        if (!visit[i]) {
            DFS(p, i);
            printf("\n");
        }
    }
}

DFS求拓扑序、逆拓扑序

在对每个点调用调用DFS时，会为每个点打上访问先后的时间戳，按时间戳先后存即为拓扑序（可以用栈），倒过来就是逆拓扑序。

Tarjan算法

Tarjian算法是基于DFS求强连通分支、割点、割边的算法，可以做到线性复杂度。

讨论割点、割边时图是无向图

最重要的两个数组：

一个是DFS给每个点v打上的时间戳dfn[v]
另一个是点u能直接通过其深搜子树所间接到达的最小时间戳low[u]

这里注意dfn[]的性质，v是u的祖先时，dfn[v]<dfn[u]。

理解关键
考虑不是根节点的u的儿子child，如果low[child]>=dfn[u]时，根据low[]的定义，child所能到达的最小时间戳已经不小于dfn[u]了，再根据dfn[]的性质，可以知道，child已经无法到达比u时间戳更靠前的点，因此当我们删掉u时，其子树的点就成为了新的连通分量，这样u就是一个割点。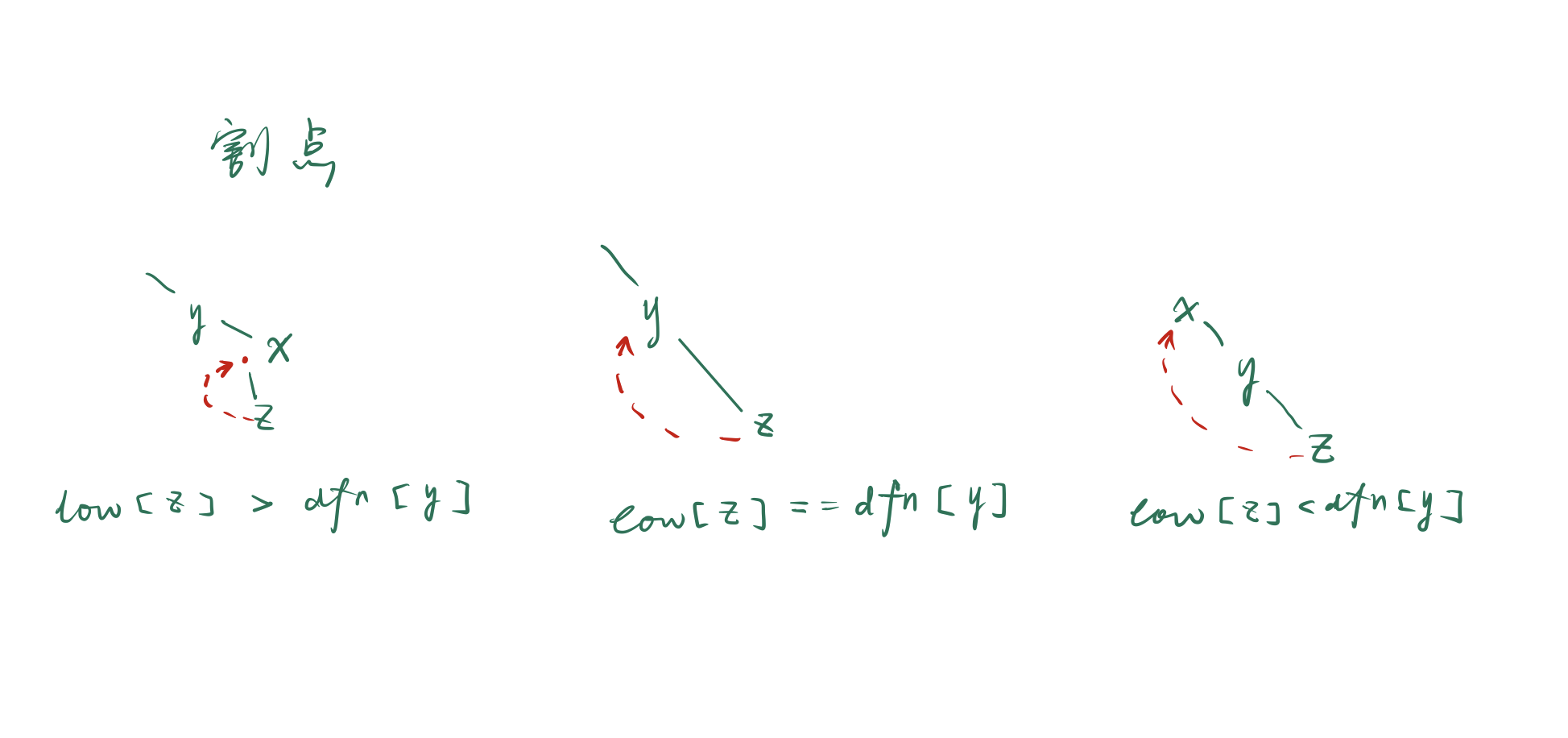

下面我们考虑割边。有了割点的铺垫，我们也可以联想到low[]>dfn[]的关系，可以画图验证我们的想法。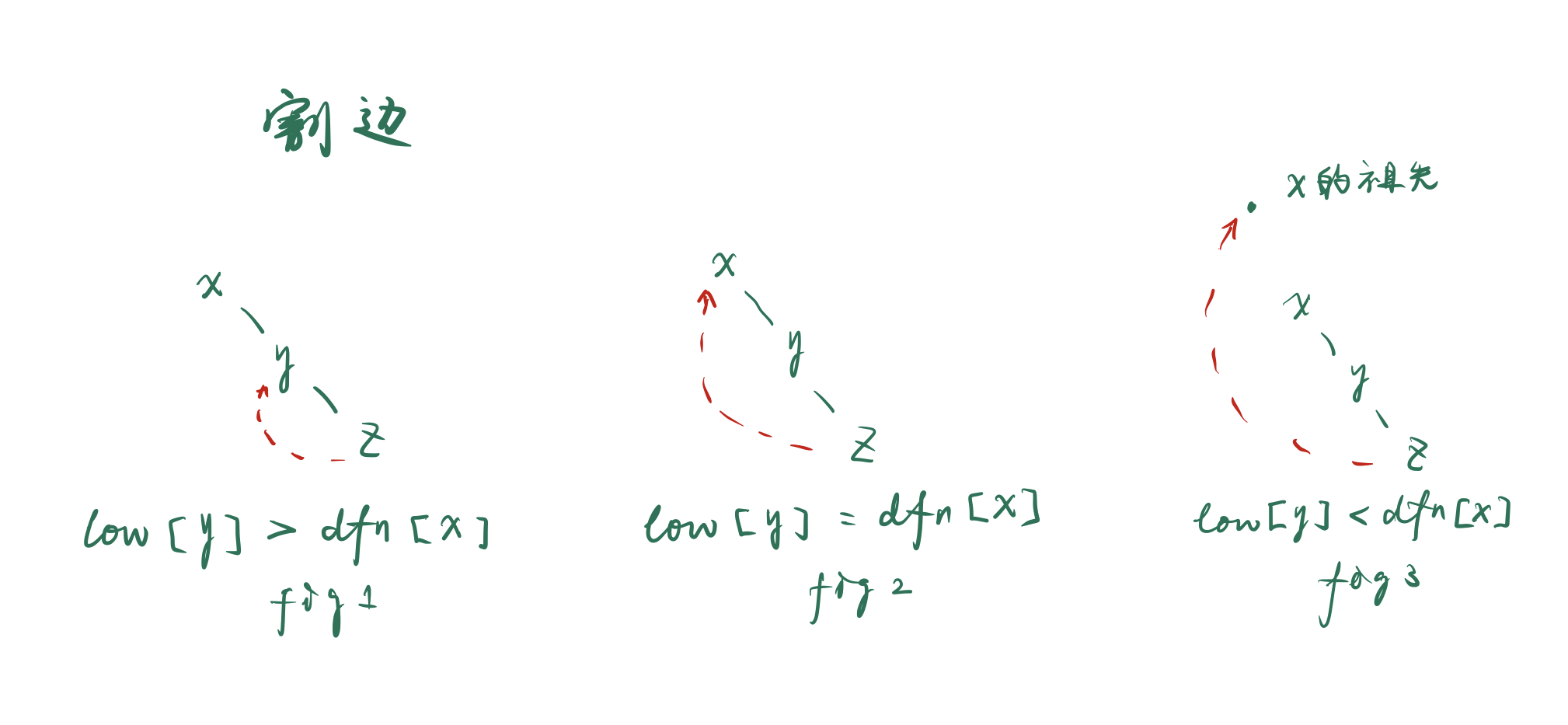

如fig.1y最早只能追溯到比x晚的点，这时如果删去x和y之间的边，就会不连通；如fig.2，y最早恰好追溯到x，这时删掉x和y之间的边仍然保持连通，fig.3更不用说。

红色标出的部分实际上正是back edge，即生成树时没用到的边

那么我们怎么更新low[]呢？

我们选定一个顶点开始dfs，访问一个点就置dfn[v]=low[v]=访问顺序，然后把这个点压入栈中
对与和v相连的所有顶点u，我们有如下两种case：

如果这个点还没有访问过，即dfn[u]未被设置过值，我们dfs(u)，并且low[v]=min{low[v],low[u]}（更新沿途的点）
如果这个点已经在栈里面了，low[v]=min{low[v],dfn[u]}（可以理解为找到背向边）

上面其实是个模板，都可以这么处理，写法可以看这里。

对于求强连通分量，我们的判断条件是low[u]==dfn[u]，也就是说到u点为止已经成环，必然是强连通的。我们对此过程的记录和上文提到的一样，使用栈。这时从栈顶出栈到u即为一个强连通分量。

int num[Max]={0},low[Max]={0},stack[Max]={0},sp=-1,
    order=0,inStack[Max]={0};
int min(int x,int y){
    return (x<=y)?x:y;
}
//这里的PrintV是cyll非要传函数指针但其实就一句printf的东西
void Tarjan(Graph G, Vertex V, void(*visit)(Vertex V)){
    num[V]=low[V]=++order;
    inStack[V]=1;
    stack[++sp]=V;
    PtrToVNode p;    
    for(p=G->Array[V];p!=NULL;p=p->Next){
        Vertex tmp=p->Vert;
        if(!num[tmp]){
            Tarjan(G,tmp,PrintV);
            low[V]=min(low[V],low[tmp]);
        }
        else if(inStack[tmp]) low[V]=min(low[V],num[tmp]);
    }
    if(num[V]==low[V]){
        inStack[V]=0;
        while(stack[sp]!=V){
            PrintV(stack[sp]);
            inStack[stack[sp]]=0;
            sp--;
        }
        PrintV(stack[sp]);
        sp--;
        printf("\n");
    }
}

Tarjan算法的模板就如上面所示了，求割点和割边只需要把判断条件改到循环里面去。

图 | Graph