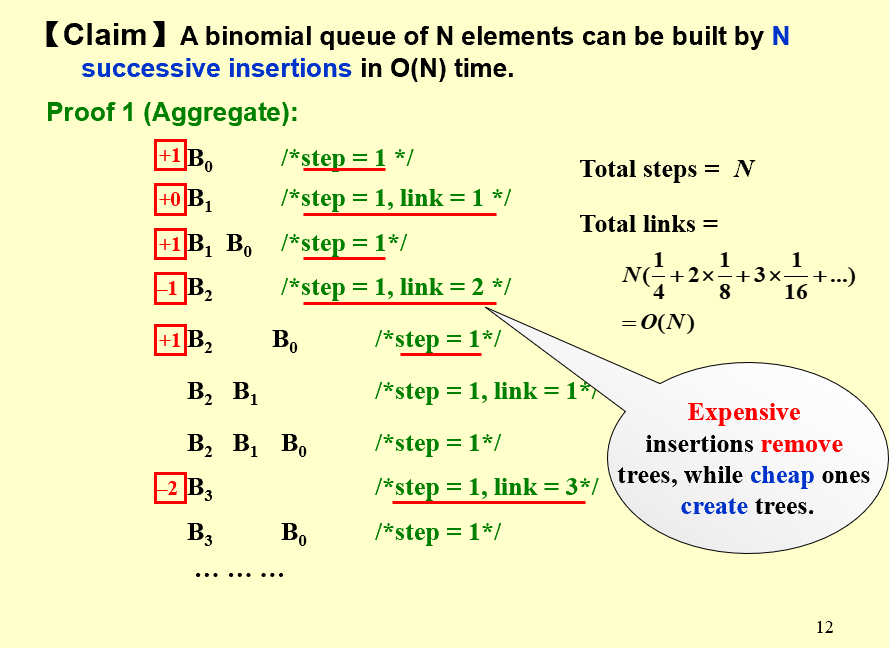
左式堆和斜堆已经很好的支持了插入、合并以及删除且都是Binomial Queue | 二项队列 - 图1级别。二项队列也支持这三种操作，且插入操作平均花费常数时间。

定义

  • 二项队列不是堆，是堆的 collection ，每个堆都是二叉树
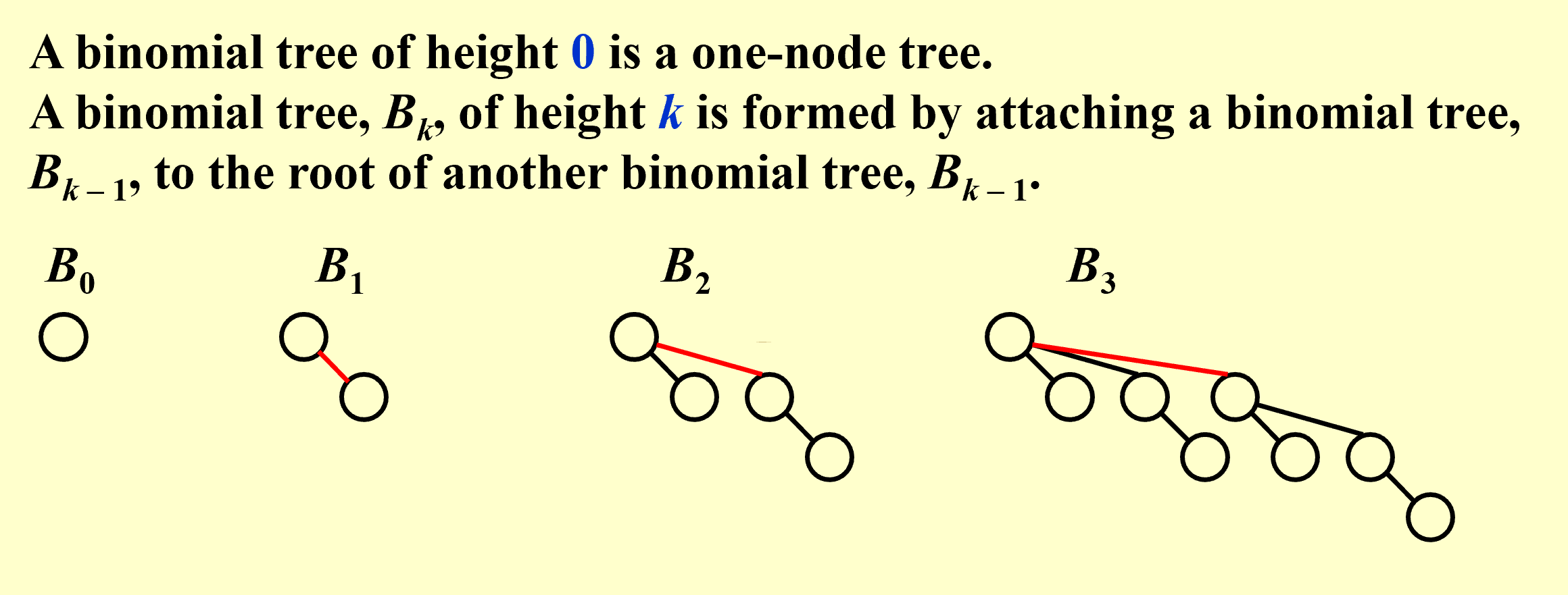
  • image.png
    • Binomial Queue | 二项队列 - 图3有Binomial Queue | 二项队列 - 图4个儿子，Binomial Queue | 二项队列 - 图5个节点，深度为Binomial Queue | 二项队列 - 图6处有Binomial Queue | 二项队列 - 图7个节点

  • 含有Binomial Queue | 二项队列 - 图8个结点的二项队列最多含有Binomial Queue | 二项队列 - 图9棵二叉树，反过来也成立

    结构

    任意大小的堆都可以表示成二项树的 collection。
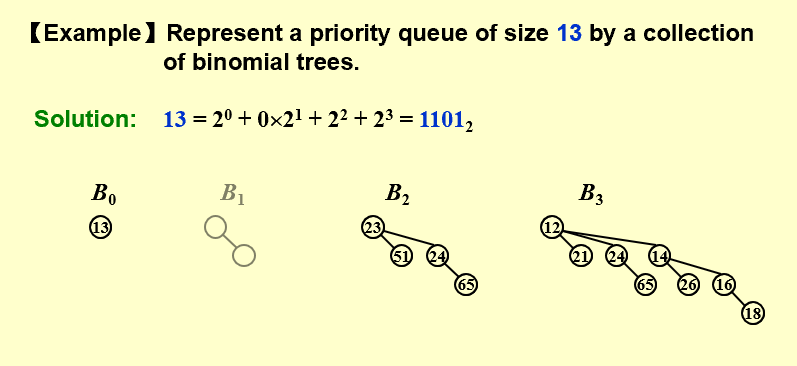
    image.png
    由于二项队列的结构较为特殊，有很多儿子，为了删除的快速和方便，我们用儿子-兄弟结构存放二项队列；为了合并的方便，从左到右子树按高度降序（descending）排列。
    image.png

    操作

    Merge & Insert

    很像合成大西瓜……
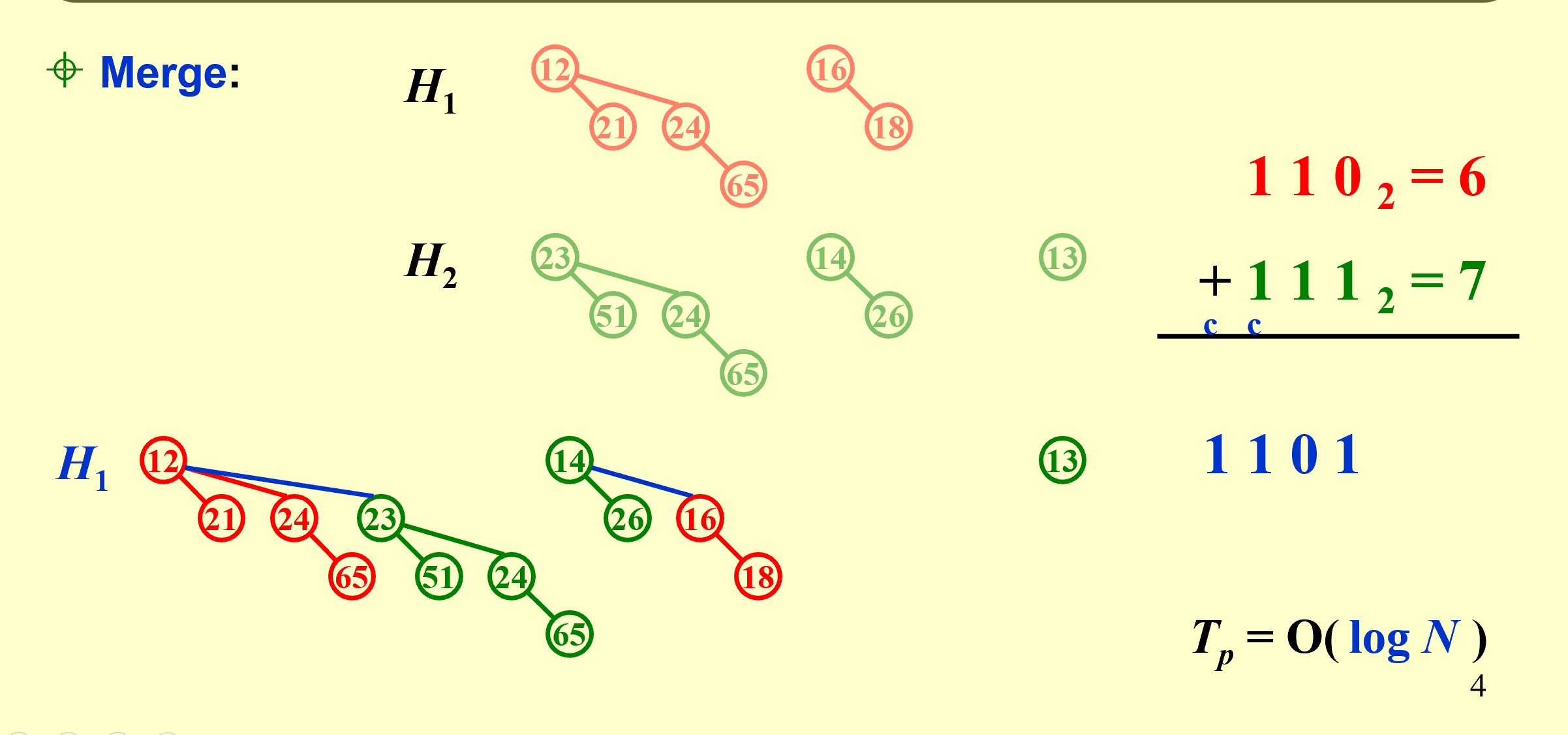
    image.png
    插入是合并的特殊情况，不多赘述。可以看出合并时实际上也是在做二进制加法，这启发我们代码也可以这样写： ```cpp / merge equal-sized T1 and T2 / //实际做合并的驱动程序 BinTree CombineTrees( BinTree T1, BinTree T2 ){
    / attach the larger one to the smaller one / if ( T1->Element > T2->Element ){

    1.   return CombineTrees( T2, T1 );

    }

    / insert T2 to the front of the children list of T1 / T2->NextSibling = T1->LeftChild; T1->LeftChild = T2;

    return T1; }

BinQueue Merge( BinQueue H1, BinQueue H2 ){
BinTree T1, T2, Carry = NULL;
int i, j; //j是计数器

  1. if ( H1->CurrentSize + H2-> CurrentSize > Capacity ){
  2.     ErrorMessage();
  3. }
  5. H1->CurrentSize += H2-> CurrentSize;
  6. for ( i=0, j=1; j<= H1->CurrentSize; i++, j*=2 ) {
  7.     T1 = H1->TheTrees[i]; T2 = H2->TheTrees[i]; /*current trees */
  9.     /* Carry T2 T1 */
  10.     //这里巧妙的一点是把指针用!!转化为0和1来计算
  11.     switch( 4*!!Carry + 2*!!T2 + !!T1 ) { 
  12.         case 0: /* 000 */
  13.         case 1: /* 001 */  break; //这两种情况都不需要合并
  15.         case 2: /* 010 */ 
  16.             H1->TheTrees[i] = T2; 
  17.             H2->TheTrees[i] = NULL; 
  18.             break;
  20.         case 4: /* 100 */  
  21.             H1->TheTrees[i] = Carry; 
  22.             Carry = NULL; 
  23.             break;
  25.         case 3: /* 011 */  
  26.             Carry = CombineTrees( T1, T2 );
  27.             H1->TheTrees[i] = H2->TheTrees[i] = NULL; 
  28.             break;
  30.         case 5: /* 101 */  
  31.             Carry = CombineTrees( T1, Carry );
  32.             H1->TheTrees[i] = NULL; 
  33.             break;
  35.         case 6: /* 110 */  
  36.             Carry = CombineTrees( T2, Carry );
  37.             H2->TheTrees[i] = NULL; 
  38.             break;
  40.         case 7: /* 111 */  
  41.             H1->TheTrees[i] = Carry; 
  42.             Carry = CombineTrees( T1, T2 ); 
  43.             H2->TheTrees[i] = NULL; 
  44.             break;
  45.     } /* end switch */
  46. } /* end for-loop */
  48. return H1;

}

  1. <a name="jVoUS"></a>
  2. ## DeleteMin
  3. 删除复杂一些，不过蕴含了合并操作<br />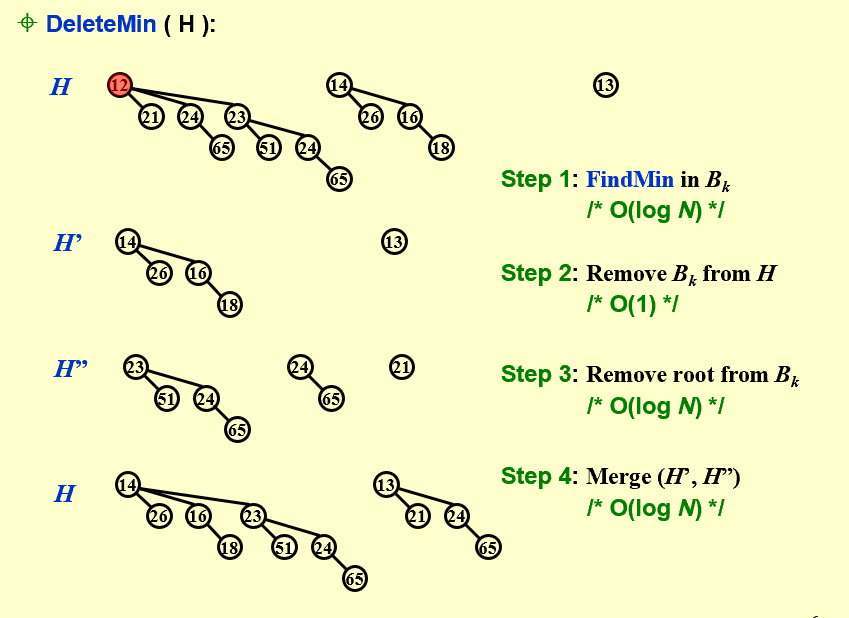![image.png](https://cdn.nlark.com/yuque/0/2022/png/22181361/1647922979053-a887c4dc-751f-4775-be15-49409d0d839e.png#clientId=u10aeb3b2-4a08-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=364&id=uc9e363e4&margin=%5Bobject%20Object%5D&name=image.png&originHeight=618&originWidth=849&originalType=binary&ratio=1&rotation=0&showTitle=false&size=53066&status=done&style=shadow&taskId=u62c33883-322e-4c00-9090-f9e1d4d1eb6&title=&width=500)
  4. ```cpp
  5. ElementType  DeleteMin( BinQueue H ){    
  6.     BinQueue DeletedQueue; 
  7.     Position DeletedTree, OldRoot;
  9.     /* the minimum item to be returned */    
  10.     ElementType MinItem = Infinity;  
  12.     /* MinTree is the index of the tree with the minimum item */
  13.     int i, j, MinTree; 
  15.     if ( IsEmpty( H ) )  {  
  16.         PrintErrorMessage();  
  17.         return –Infinity; 
  18.     }
  20.     /* Step 1: find the minimum item */
  21.     for ( i = 0; i < MaxTrees; i++) {  
  22.         if( H->TheTrees[i] && H->TheTrees[i]->Element < MinItem ) { 
  23.         MinItem = H->TheTrees[i]->Element;  MinTree = i;    
  24.         } 
  25.     } 
  27.     DeletedTree = H->TheTrees[ MinTree ];  
  28.     /* Step 2: remove the MinTree from H => H’ */ 
  29.     H->TheTrees[ MinTree ] = NULL;   
  31.     /* Step 3.1: remove the root */ 
  32.     OldRoot = DeletedTree;   
  33.     DeletedTree = DeletedTree->LeftChild;   
  34.     free(OldRoot);
  36.     /* Step 3.2: create H” */ 
  37.     DeletedQueue = Initialize();   
  38.     DeletedQueue->CurrentSize = ( 1<<MinTree ) – 1;  /* 2^MinTree – 1 */
  40.     //这里的做法是将删除元素后产生的子树先整理成二项队列，以便后续合并
  41.     for ( j = MinTree – 1; j >= 0; j – – ) {  
  42.         DeletedQueue->TheTrees[j] = DeletedTree;
  43.         DeletedTree = DeletedTree->NextSibling;
  44.         DeletedQueue->TheTrees[j]->NextSibling = NULL;
  45.     } 
  47.     H->CurrentSize  –= DeletedQueue->CurrentSize + 1;
  49.     /* Step 4: merge H’ and H” */ 
  50.     H = Merge( H, DeletedQueue );
  52.     return MinItem;
  53. }

摊还分析

image.png
image.png
image.png