1. 树

1.1 【简单】二叉树的前序遍历（144）

image.png

  1. /**
  2.  * 树的前序遍历
  3.  */
  4. public List<Integer> preorderTraversal(TreeNode root) {
  5.     List<Integer> list = new ArrayList<>();
  6.     Stack<TreeNode> stack = new Stack<>();
  7.     while (root != null || !stack.isEmpty()) {
  8.         while (root != null) {
  9.             list.add(root.value);
  10.             stack.push(root);
  11.             root = root.left;
  12.         }
  13.         if (!stack.isEmpty()) {
  14.             root = stack.pop();
  15.             root = root.right;
  16.         }
  17.     }
  18.     return list;
  19. }

1.2 【简单】二叉树的中序遍历（94）

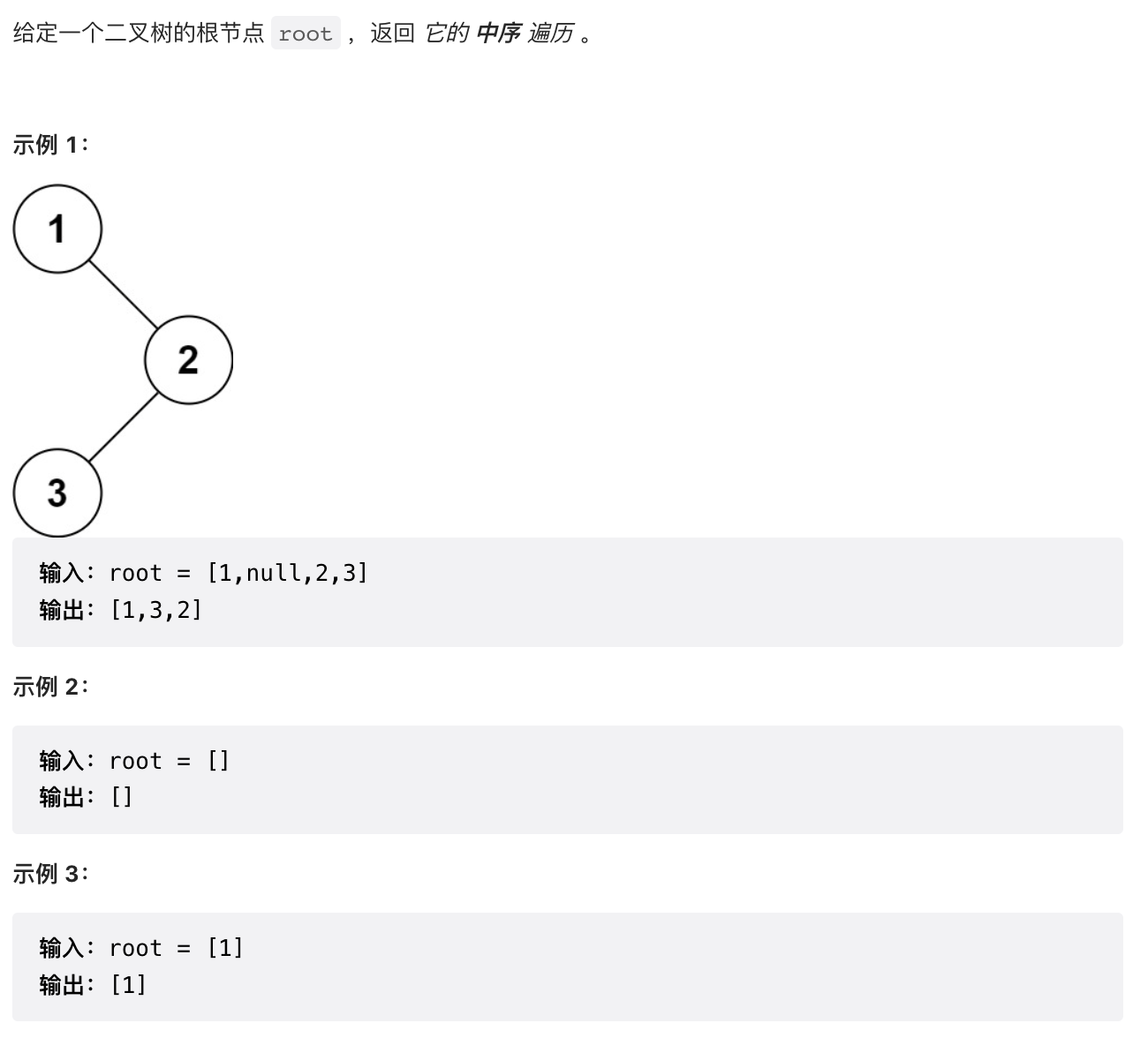
image.png

  1. /**
  2.  * 树的中序遍历
  3.  */
  4. public List<Integer> inorderTraversal(TreeNode root) {
  5.     List<Integer> result = new ArrayList<>();
  6.     Stack<TreeNode> stack = new Stack<>();
  7.     while (root != null || !stack.isEmpty()) {
  8.         while (root != null) {
  9.             stack.push(root);
  10.             root = root.left;
  11.         }
  12.         if (!stack.isEmpty()) {
  13.             root = stack.pop();
  14.             result.add(root.value);
  15.             root = root.right;
  16.         }
  17.     }
  18.     return result;
  19. }

1.3 【简单】二叉树的后序遍历（145）

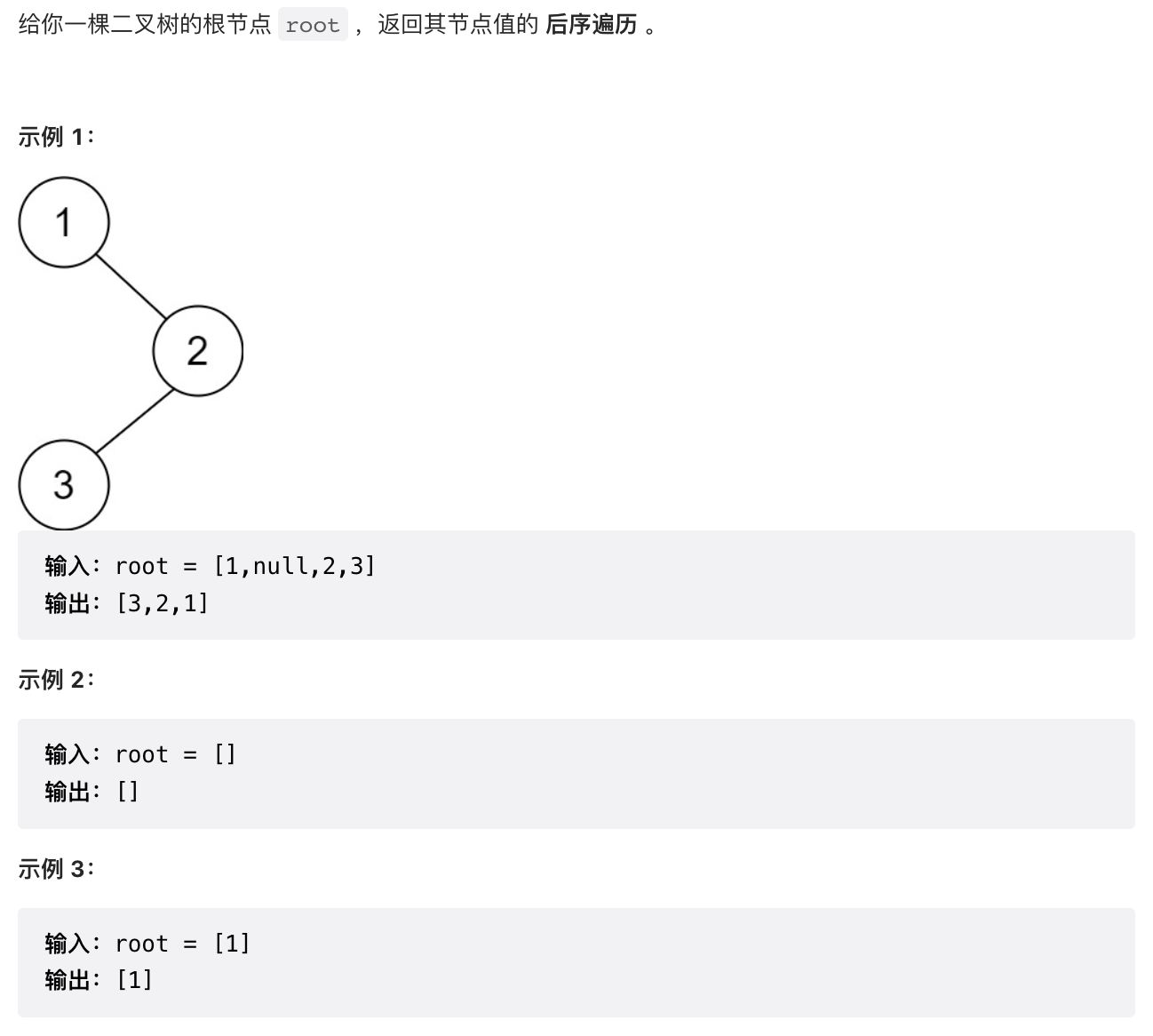
image.png

  1. /**
  2.  * 树的后序遍历
  3.  */
  4. public List<Integer> postorderTraversal(TreeNode root) {
  5.     List<Integer> result = new ArrayList<>();
  6.     Stack<TreeNode> stack1 = new Stack<>();
  7.     Stack<Integer> stack2 = new Stack<>();
  8.     int left = 1;
  9.     int right = 2;
  10.     while (root != null || !stack1.isEmpty()) {
  11.         while (root != null) {
  12.             stack1.push(root);
  13.             stack2.push(left);
  14.             root = root.left;
  15.         }
  16.         while (!stack1.isEmpty() && stack2.peek() == right) {
  17.             stack2.pop();
  18.             result.add(stack1.pop().value);
  19.         }
  20.         if (!stack1.isEmpty() && stack2.peek() == left) {
  21.             root = stack1.peek().right;
  22.             stack2.pop();
  23.             stack2.push(right);
  24.         }
  25.     }
  26.     return result;
  27. }

1.4 【简单】N 叉树的前序遍历（589）

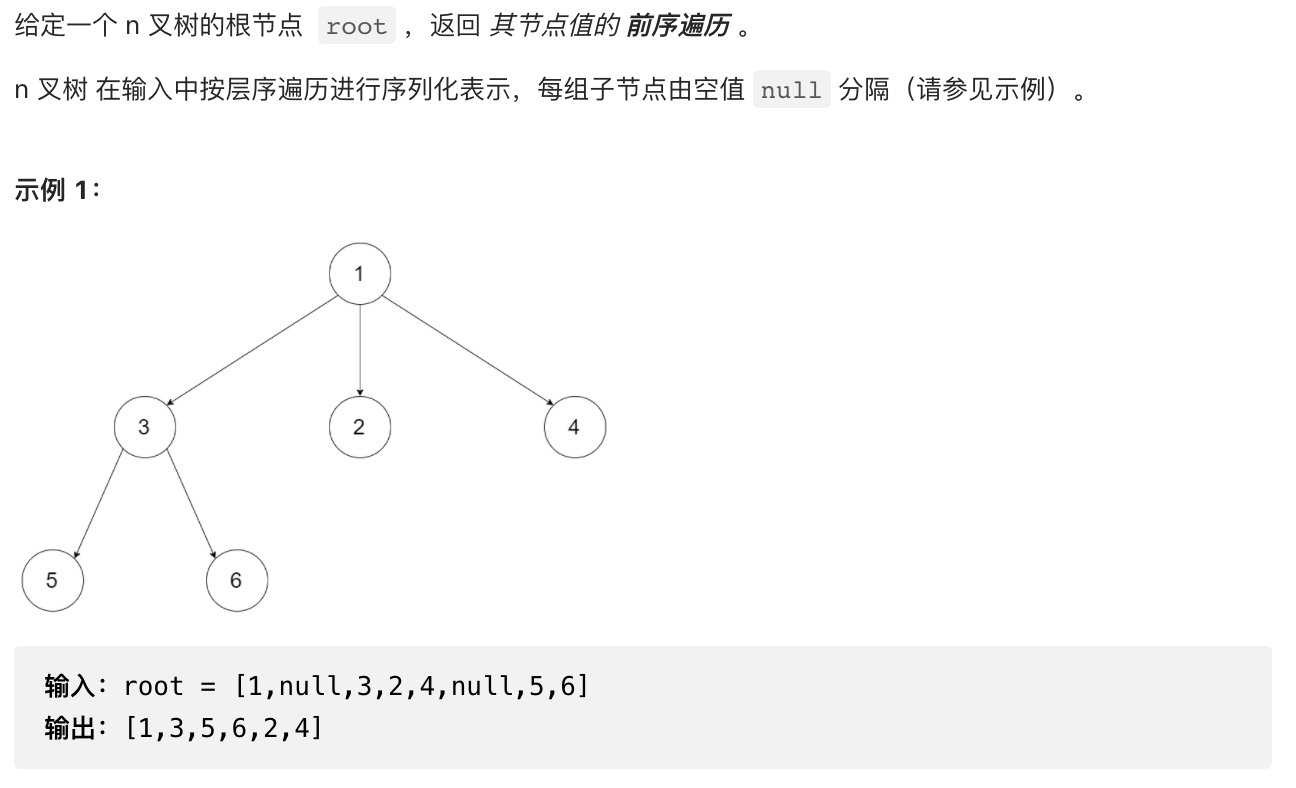
image.png

  1. /**
  2.  * N叉树的前序遍历
  3.  */
  4. public List<Integer> preorder(Node root) {
  5.     List<Integer> res = new ArrayList<>();
  6.     if (root == null) {
  7.         return res;
  8.     }
  9.     Deque<Node> stack = new ArrayDeque<>();
  10.     stack.push(root);
  11.     while (!stack.isEmpty()) {
  12.         Node node = stack.pop();
  13.         res.add(node.val);
  14.         for (int i = node.children.size() - 1; i >= 0; --i) {
  15.             stack.push(node.children.get(i));
  16.         }
  17.     }
  18.     return res;
  19. }

1.5 【简单】N 叉树的后序遍历（590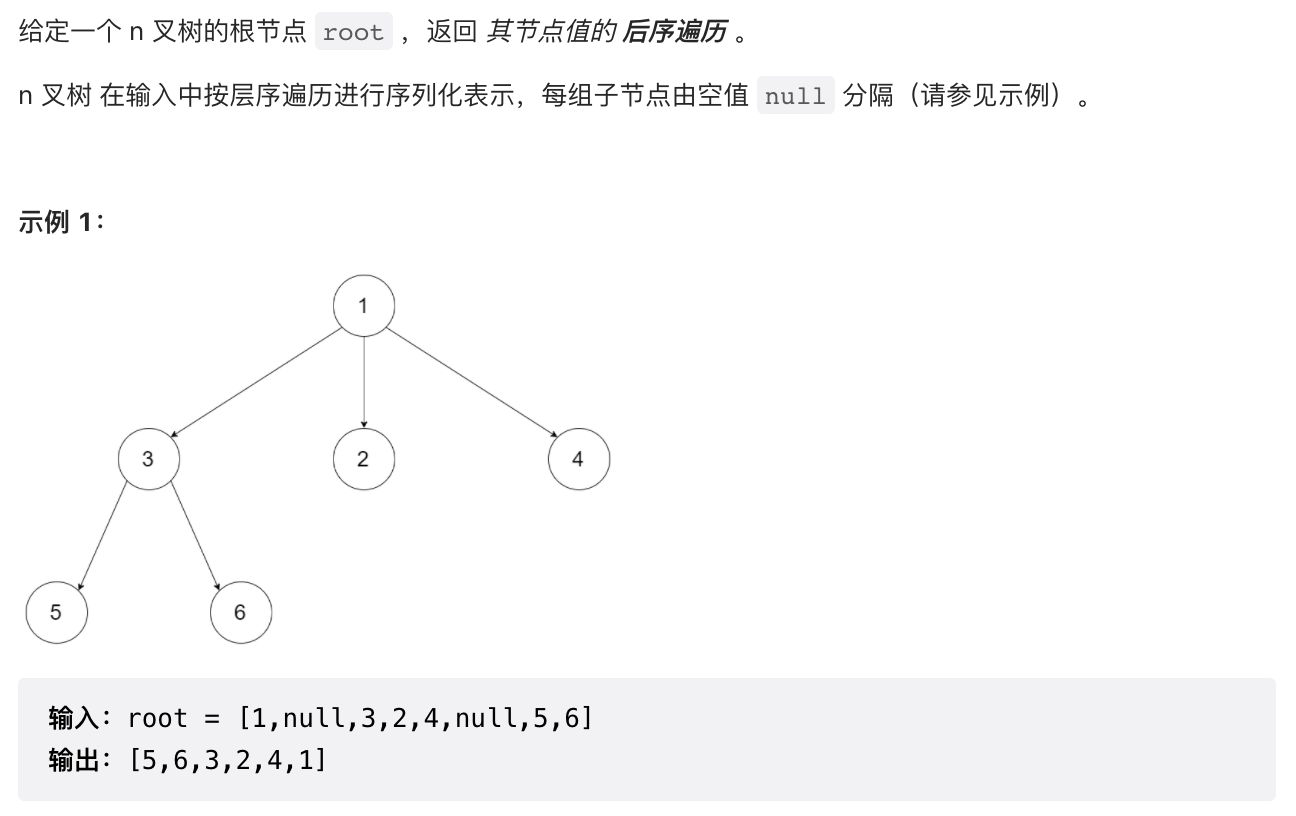）image.png

  1. /**
  2.  * N叉树的后序遍历，可以利用中右左反转即为左右中（后序）
  3.  */
  4. public List<Integer> postorder(Node root) {
  5.     List<Integer> res = new ArrayList<>();
  6.     if (root == null) {
  7.         return res;
  8.     }
  9.     Deque<Node> stack = new ArrayDeque<>();
  10.     stack.push(root);
  11.     while (!stack.isEmpty()) {
  12.         Node node = stack.pop();
  13.         res.add(node.val);
  14.         for (Node item : node.children) {
  15.             stack.push(item);
  16.         }
  17.     }
  18.     Collections.reverse(res);
  19.     return res;
  20. }

1.6 【中等】N 叉树的层序遍历（429）

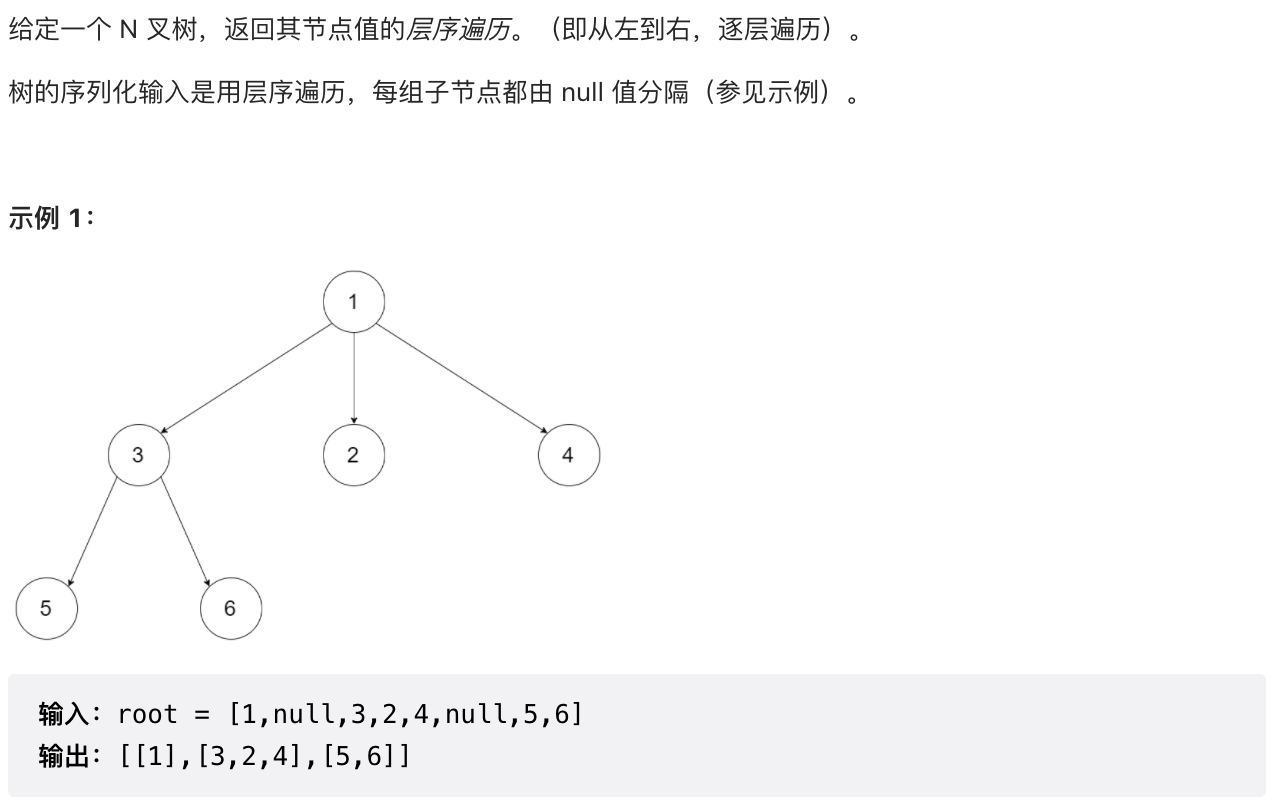
image.png

  1. /**
  2.  * 队列即可，与二叉树的层序遍历相似
  3.  */
  4. public List<List<Integer>> levelOrder(Node root) {
  5.     List<List<Integer>> ret = new ArrayList<>();
  6.     if (root == null) {
  7.         return ret;
  8.     }
  9.     Queue<Node> queue = new LinkedList<>();
  10.     queue.offer(root);
  11.     while (!queue.isEmpty()) {
  12.         List<Integer> level = new ArrayList<>();
  13.         int currentLevelSize = queue.size();
  14.         for (int i = 1; i <= currentLevelSize; ++i) {
  15.             Node node = queue.poll();
  16.             level.add(node.val);
  17.             if (node.children != null) {
  18.                 for (Node child : node.children) {
  19.                     queue.offer(child);
  20.                 }
  21.             }
  22.         }
  23.         ret.add(level);
  24.     }
  25.     return ret;
  26. }

1.7 【中等】从前序与中序遍历序列构造二叉树（105）

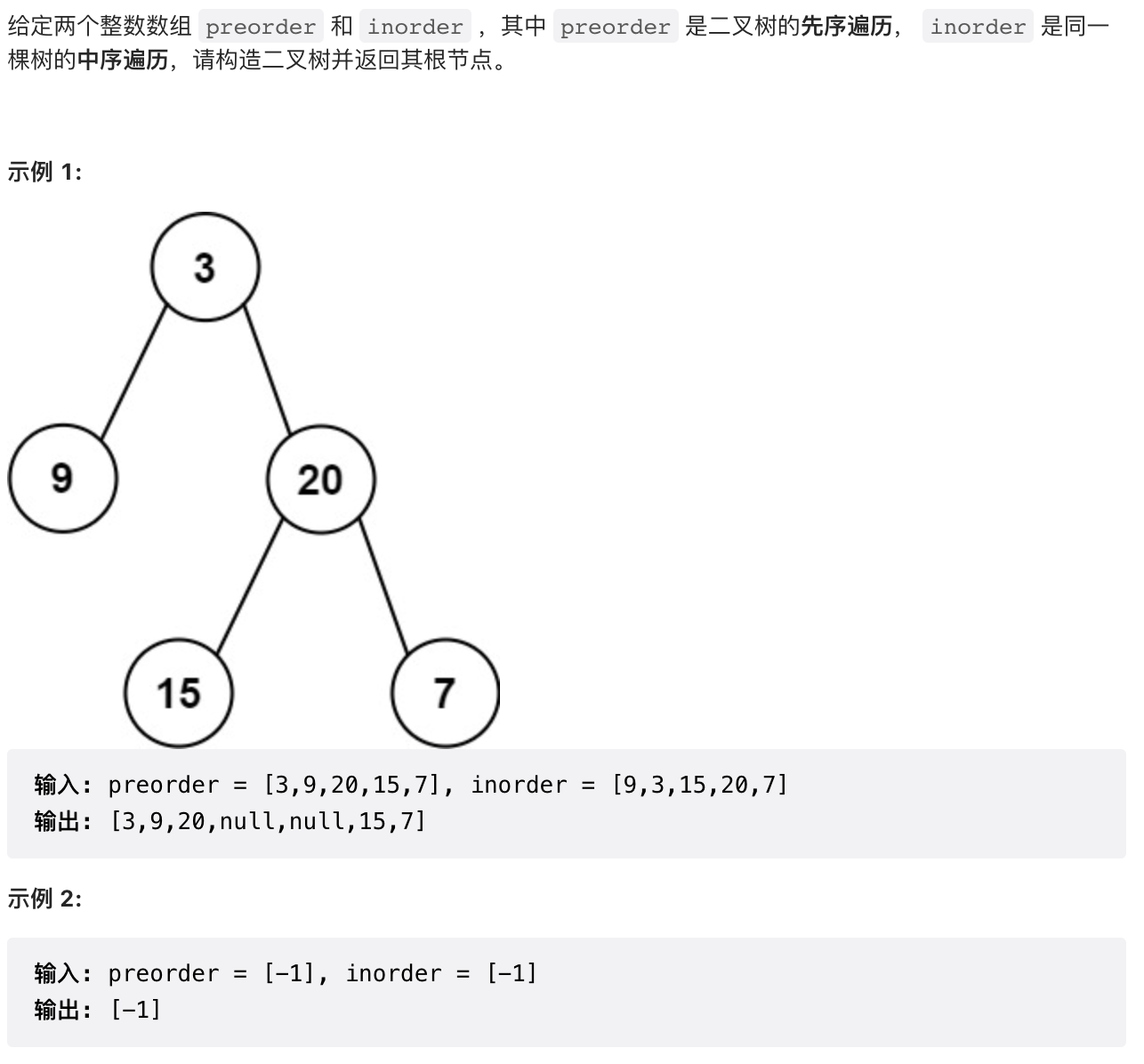
image.png
递归

  1. /**
  2.  * 递归构建左右节点，先统计出各自的数量以及确定index
  3.  */
  4. public class BuildTree {
  5.     private Map<Integer, Integer> indexMap;
  7.     public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorderLeft, int preorderRight, int inorderLeft, int inorderRight) {
  8.         if (preorderLeft > preorderRight) {
  9.             return null;
  10.         }
  12.         // 前序遍历中的第一个节点就是根节点
  13.         int preorderRoot = preorderLeft;
  14.         // 在中序遍历中定位根节点
  15.         int inorderRoot = indexMap.get(preorder[preorderRoot]);
  17.         // 先把根节点建立出来
  18.         TreeNode root = new TreeNode(preorder[preorderRoot]);
  19.         // 得到左子树中的节点数目
  20.         int sizeLeftSubtree = inorderRoot - inorderLeft;
  21.         // 递归地构造左子树，并连接到根节点
  22.         // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
  23.         root.left = myBuildTree(preorder, inorder, preorderLeft + 1, preorderLeft + sizeLeftSubtree, inorderLeft, inorderRoot - 1);
  24.         // 递归地构造右子树，并连接到根节点
  25.         // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
  26.         root.right = myBuildTree(preorder, inorder, preorderLeft + sizeLeftSubtree + 1, preorderRight, inorderRoot + 1, inorderRight);
  27.         return root;
  28.     }
  30.     public TreeNode buildTree(int[] preorder, int[] inorder) {
  31.         int n = preorder.length;
  32.         // 构造哈希映射，帮助我们快速定位根节点
  33.         indexMap = new HashMap<>();
  34.         for (int i = 0; i < n; i++) {
  35.             indexMap.put(inorder[i], i);
  36.         }
  37.         return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
  38.     }
  39. }

非递归

  1. /**
  2.  * 有点难，记下关键步骤
  3.  */
  4. public TreeNode myBuildTree(int[] preorder, int[] inorder) {
  5.     if (preorder == null || preorder.length == 0) {
  6.         return null;
  7.     }
  8.     // 前序遍历最左边元素即为根节点
  9.     TreeNode root = new TreeNode(preorder[0]);
  10.     Deque<TreeNode> stack = new LinkedList<>();
  11.     stack.push(root);
  12.     int inorderIndex = 0;
  13.     for (int i = 1; i < preorder.length; i++) {
  14.         int preorderVal = preorder[i];
  15.         TreeNode node = stack.peek();
  16.         // 如果相等了就是当前节点下的最左节点
  17.         if (node.value != inorder[inorderIndex]) {
  18.             node.left = new TreeNode(preorderVal);
  19.             stack.push(node.left);
  20.         } else {
  21.             // 如果不等就是右节点，否则一直出栈
  22.             while (!stack.isEmpty() && stack.peek().value == inorder[inorderIndex]) {
  23.                 node = stack.pop();
  24.                 inorderIndex++;
  25.             }
  26.             node.right = new TreeNode(preorderVal);
  27.             stack.push(node.right);
  28.         }
  29.     }
  30.     return root;
  31. }

1.8 【中等】根据前序和后序遍历构造二叉树（889）

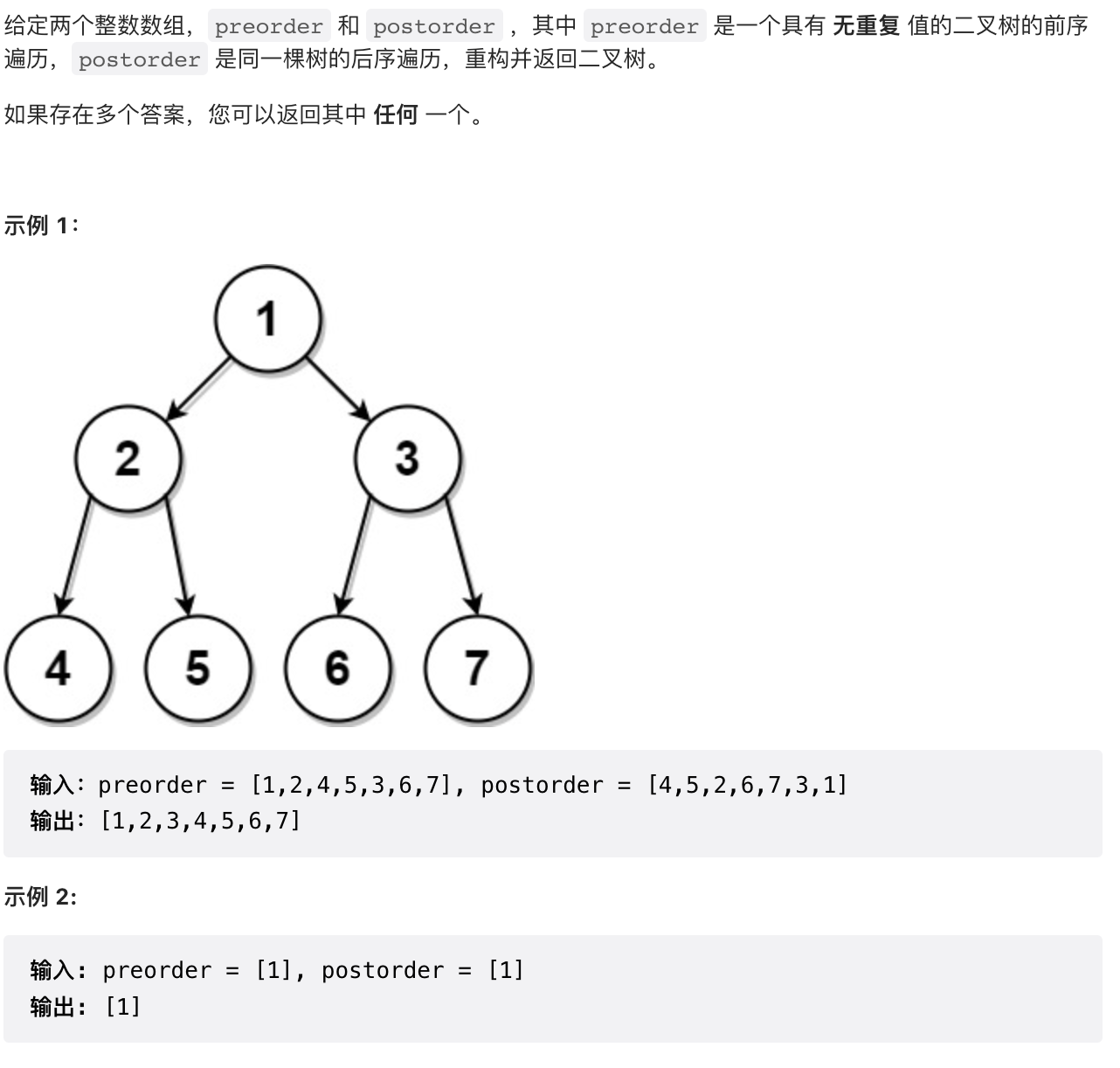
image.png

  1. /**
  2.  * 我们令左分支有 L 个节点。我们知道左分支的头节点为 pre[1]，但它也出现在左分支的后序遍历的最后。
  3.  */
  4. public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
  5.     int N = preorder.length;
  6.     if (N == 0) {
  7.         return null;
  8.     }
  9.     TreeNode root = new TreeNode(preorder[0]);
  10.     if (N == 1) {
  11.         return root;
  12.     }
  13.     int L = 0;
  14.     for (int i = 0; i < N; ++i) {
  15.         if (postorder[i] == preorder[1]) {
  16.             L = i + 1;
  17.         }
  18.     }
  19.     root.left = constructFromPrePost(Arrays.copyOfRange(preorder, 1, L + 1),
  20.             Arrays.copyOfRange(postorder, 0, L));
  21.     root.right = constructFromPrePost(Arrays.copyOfRange(preorder, L + 1, N),
  22.             Arrays.copyOfRange(postorder, L, N - 1));
  23.     return root;
  24. }

1.9 【中等】从中序与后序遍历序列构造二叉树（106）

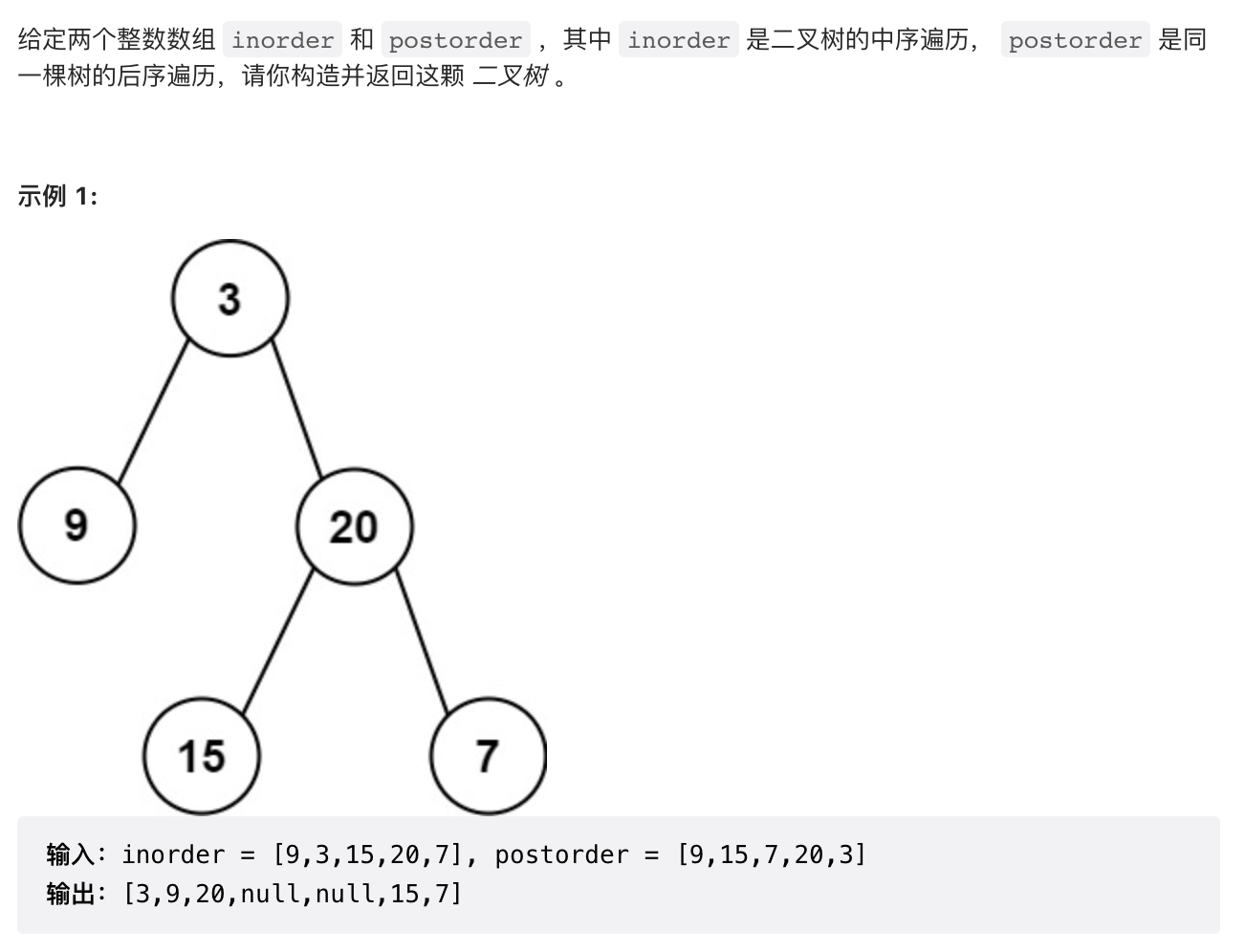
image.png
递归

  1. /**
  2.  * 后序遍历末尾元素即为根节点，在根据中序遍历进行构建左右子树
  3.  */
  4. public class BuildTree {
  5.     int postIdx;
  6.     int[] postorder;
  7.     int[] inorder;
  8.     Map<Integer, Integer> idxMap = new HashMap<>();
  10.     public TreeNode helper(int inLeft, int inRight) {
  11.         // 如果这里没有节点构造二叉树了，就结束
  12.         if (inLeft > inRight) {
  13.             return null;
  14.         }
  16.         // 选择 postIdx 位置的元素作为当前子树根节点
  17.         int rootVal = postorder[postIdx];
  18.         TreeNode root = new TreeNode(rootVal);
  20.         // 根据 root 所在位置分成左右两棵子树
  21.         int index = idxMap.get(rootVal);
  23.         // 下标减一
  24.         postIdx--;
  25.         // 构造右子树
  26.         root.right = helper(index + 1, inRight);
  27.         // 构造左子树
  28.         root.left = helper(inLeft, index - 1);
  29.         return root;
  30.     }
  32.     public TreeNode buildTree(int[] inorder, int[] postorder) {
  33.         this.postorder = postorder;
  34.         this.inorder = inorder;
  35.         // 从后序遍历的最后一个元素开始
  36.         postIdx = postorder.length - 1;
  38.         // 建立（元素，下标）键值对的哈希表
  39.         int idx = 0;
  40.         for (Integer val : inorder) {
  41.             idxMap.put(val, idx++);
  42.         }
  44.         return helper(0, inorder.length - 1);
  45.     }
  46. }

非递归

  1. /**
  2.  * 中序遍历反一下即为右中左，后序遍历反一下为中右左，所以用跟1.7的方法即可
  3.  */
  4. public TreeNode buildTree2(int[] inorder, int[] postorder) {
  5.     if (postorder == null || postorder.length == 0) {
  6.         return null;
  7.     }
  8.     TreeNode root = new TreeNode(postorder[postorder.length - 1]);
  9.     Deque<TreeNode> stack = new LinkedList<>();
  10.     stack.push(root);
  11.     int inorderIndex = inorder.length - 1;
  12.     for (int i = postorder.length - 2; i >= 0; i--) {
  13.         int postorderVal = postorder[i];
  14.         TreeNode node = stack.peek();
  15.         if (node.value != inorder[inorderIndex]) {
  16.             node.right = new TreeNode(postorderVal);
  17.             stack.push(node.right);
  18.         } else {
  19.             while (!stack.isEmpty() && stack.peek().value == inorder[inorderIndex]) {
  20.                 node = stack.pop();
  21.                 inorderIndex--;
  22.             }
  23.             node.left = new TreeNode(postorderVal);
  24.             stack.push(node.left);
  25.         }
  26.     }
  27.     return root;
  28. }

1.10 【中等】路径总和 II（113）

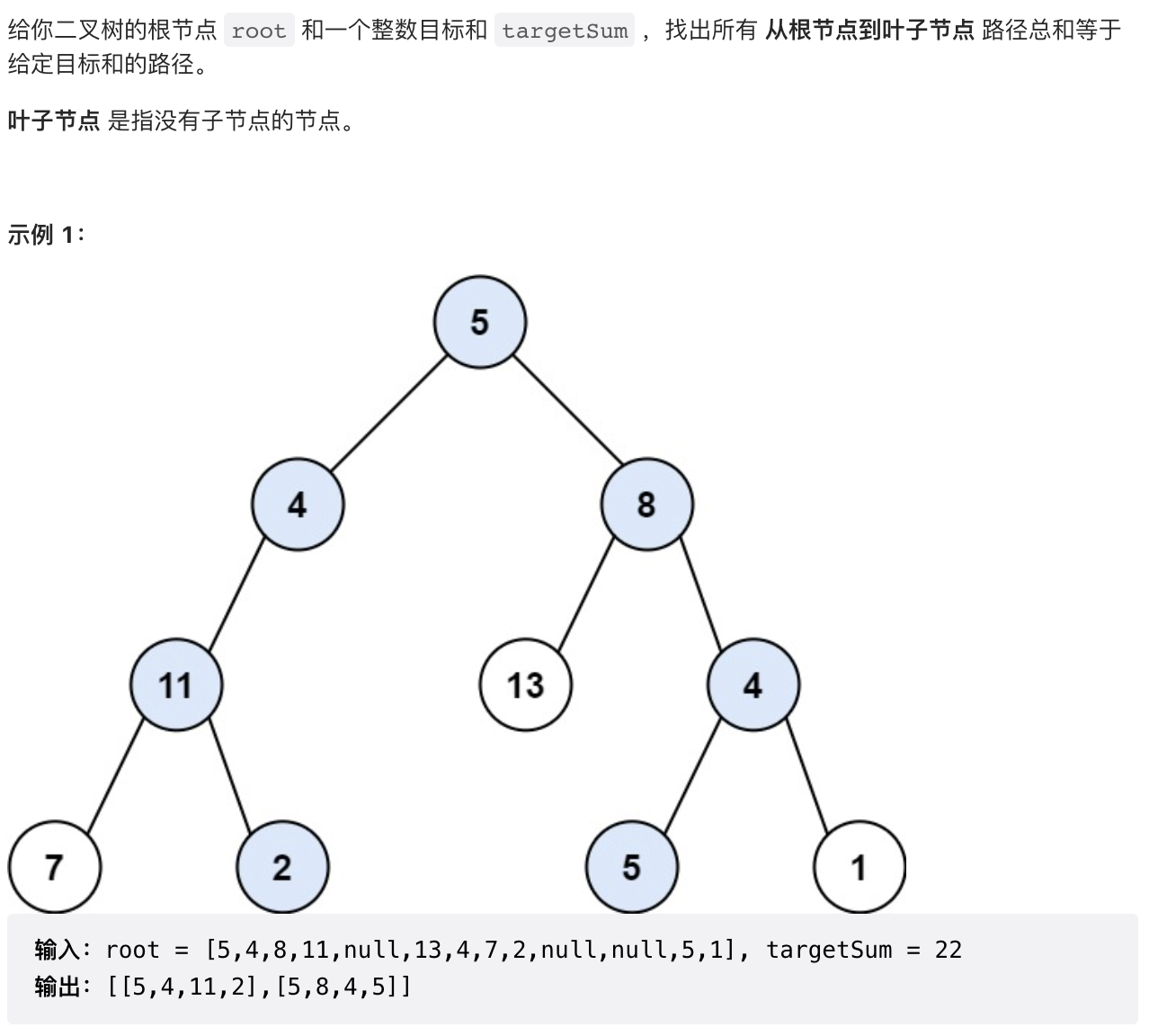
image.png
深度优先搜索

  1. /**
  2.  * 深度优先搜索，dfs递归
  3.  */
  4. public class PathSum {
  5.     List<List<Integer>> ret = new LinkedList<>();
  6.     Deque<Integer> path = new LinkedList<>();
  8.     public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
  9.         dfs(root, targetSum);
  10.         return ret;
  11.     }
  13.     public void dfs(TreeNode root, int targetSum) {
  14.         if (root == null) {
  15.             return;
  16.         }
  17.         path.offerLast(root.value);
  18.         targetSum -= root.value;
  19.         if (root.left == null && root.right == null && targetSum == 0) {
  20.             ret.add(new LinkedList<>(path));
  21.         }
  22.         dfs(root.left, targetSum);
  23.         dfs(root.right, targetSum);
  24.         path.pollLast();
  25.     }
  26. }

广度优先搜索

  1. /**
  2.  * 广度优先搜索
  3.  */
  4. public class PathSum {
  5.     List<List<Integer>> ret = new LinkedList<>();
  6.     // key:子节点，value:父节点
  7.     Map<TreeNode, TreeNode> map = new HashMap<>();
  9.     public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
  10.         if (root == null) {
  11.             return ret;
  12.         }
  14.         Queue<TreeNode> queueNode = new LinkedList<>();
  15.         Queue<Integer> queueSum = new LinkedList<>();
  16.         queueNode.offer(root);
  17.         queueSum.offer(0);
  19.         while (!queueNode.isEmpty()) {
  20.             TreeNode node = queueNode.poll();
  21.             int rec = queueSum.poll() + node.value;
  23.             if (node.left == null && node.right == null) {
  24.                 if (rec == targetSum) {
  25.                     // 符合路径，构造路径返回
  26.                     getPath(node);
  27.                 }
  28.             } else {
  29.                 if (node.left != null) {
  30.                     // 左节点添加
  31.                     map.put(node.left, node);
  32.                     queueNode.offer(node.left);
  33.                     queueSum.offer(rec);
  34.                 }
  35.                 if (node.right != null) {
  36.                     // 右节点添加
  37.                     map.put(node.right, node);
  38.                     queueNode.offer(node.right);
  39.                     queueSum.offer(rec);
  40.                 }
  41.             }
  42.         }
  44.         return ret;
  45.     }
  47.     public void getPath(TreeNode node) {
  48.         List<Integer> temp = new LinkedList<>();
  49.         while (node != null) {
  50.             temp.add(node.value);
  51.             node = map.get(node);
  52.         }
  53.         // 倒序节点
  54.         Collections.reverse(temp);
  55.         ret.add(new LinkedList<>(temp));
  56.     }
  57. }

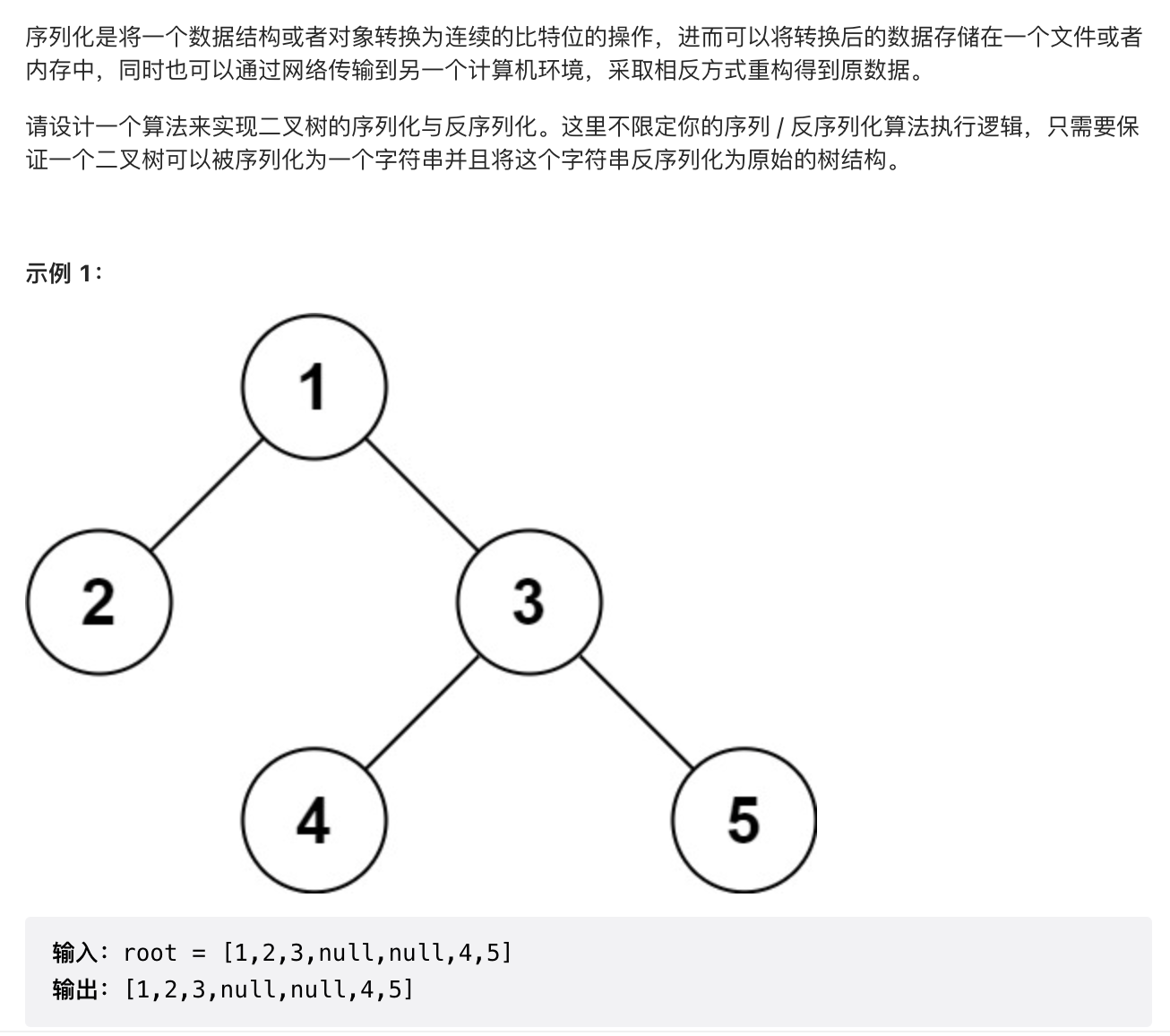
1.11 【困难】剑指 Offer II 048. 序列化与反序列化二叉树

image.png

  1. /**
  2.  * 递归遍历即可
  3.  */
  4. public String serialize(TreeNode root) {
  5.     return rserialize(root,"");
  6. }
  8. public TreeNode deserialize(String data) {
  9.     String[] dataArray = data.split(",");
  10.     List<String> dataList = new LinkedList<>(Arrays.asList(dataArray));
  11.     return rdeserialize(dataList);
  12. }
  14. public String rserialize(TreeNode root, String str) {
  15.     if (root == null) {
  16.         str += "None,";
  17.     } else {
  18.         str += root.value + ",";
  19.         str = rserialize(root.left, str);
  20.         str = rserialize(root.right, str);
  21.     }
  22.     return str;
  23. }
  25. public TreeNode rdeserialize(List<String> dataList) {
  26.     if ("None".equals(dataList.get(0))) {
  27.         dataList.remove(0);
  28.         return null;
  29.     }
  30.     TreeNode root = new TreeNode(Integer.valueOf(dataList.get(0)));
  31.     dataList.remove(0);
  32.     root.left = rdeserialize(dataList);
  33.     root.right = rdeserialize(dataList);
  34.     return root;
  35. }

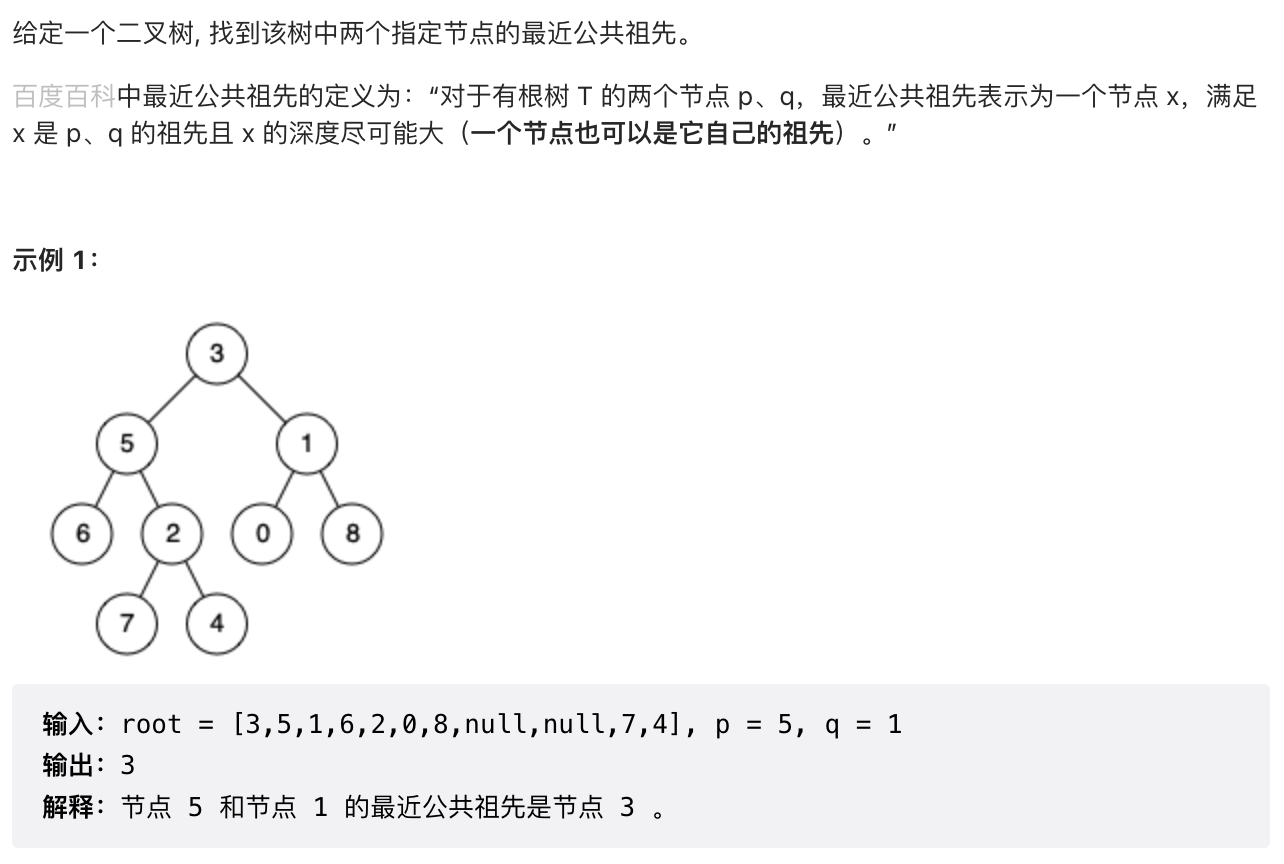
1.12 【中等】二叉树的最近公共祖先

image.png

  1. class Solution {
  3.     private TreeNode ans;
  5.     public Solution() {
  6.         this.ans = null;
  7.     }
  9.     private boolean dfs(TreeNode root, TreeNode p, TreeNode q) {
  10.         if (root == null) return false;
  11.         boolean lson = dfs(root.left, p, q);
  12.         boolean rson = dfs(root.right, p, q);
  13.         if ((lson && rson) || ((root.val == p.val || root.val == q.val) && (lson || rson))) {
  14.             ans = root;
  15.         } 
  16.         return lson || rson || (root.val == p.val || root.val == q.val);
  17.     }
  19.     public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
  20.         this.dfs(root, p, q);
  21.         return this.ans;
  22.     }
  23. }

定义 fx 表示 x 节点的子树中是否包含 p 节点或 q 节点，如果包含为 true，否则为 false

2. 递归

2.1 【简单】爬楼梯（70）

image.png
递归

  1. public int climbStairs(int n) {
  2.     if (n <= 2) {
  3.         return n;
  4.     }
  5.     return climbStairs( n - 1 ) + climbStairs( n - 2 );
  6. }

非递归

  1. public int climbStairs(int n) {
  2.     int p = 0, q = 0, r = 1;
  3.     for (int i = 1; i <= n; ++i) {
  4.         p = q;
  5.         q = r;
  6.         r = p + q;
  7.     }
  8.     return r;
  9. }

2.2 【中等】括号生成（22）

image.png
递归

  1. /**
  2.  * 递归
  3.  */
  4. public class GenerateParenthesis {
  5.     List<String> res = new ArrayList<>();
  6.     public List<String> generateParenthesis(int n) {
  7.         if (n <= 0) {
  8.             return res;
  9.         }
  10.         getParenthesis("", n, n);
  11.         return res;
  12.     }
  13.     private void getParenthesis(String str, int left, int right) {
  14.         if (left == 0 && right == 0) {
  15.             res.add(str);
  16.             return;
  17.         }
  18.         if (left == right) {
  19.             //剩余左右括号数相等，下一个只能用左括号
  20.             getParenthesis(str + "(", left - 1, right);
  21.         } else if (left < right) {
  22.             //剩余左括号小于右括号，下一个可以用左括号也可以用右括号
  23.             if (left > 0) {
  24.                 getParenthesis(str + "(", left - 1, right);
  25.             }
  26.             getParenthesis(str + ")", left, right - 1);
  27.         }
  28.     }
  29. }

回溯

  1. /**
  2.  * 回溯
  3.  */
  4. public class GenerateParenthesis2 {
  5.     public List<String> generateParenthesis(int n) {
  6.         List<String> ans = new ArrayList<>();
  7.         backtrack(ans, new StringBuilder(), 0, 0, n);
  8.         return ans;
  9.     }
  11.     public void backtrack(List<String> ans, StringBuilder cur, int open, int close, int max) {
  12.         if (cur.length() == max * 2) {
  13.             ans.add(cur.toString());
  14.             return;
  15.         }
  16.         if (open < max) {
  17.             cur.append('(');
  18.             backtrack(ans, cur, open + 1, close, max);
  19.             // 删除最后一个元素，方便寻找其他可能性
  20.             cur.deleteCharAt(cur.length() - 1);
  21.         }
  22.         if (close < open) {
  23.             cur.append(')');
  24.             backtrack(ans, cur, open, close + 1, max);
  25.             cur.deleteCharAt(cur.length() - 1);
  26.         }
  27.     }
  28. }

2.3 【简单】汉诺塔问题（面试题 08.06.）

image.png

  1. /**
  2.  * 将 A 上的所有盘子，借助 B，移动到C 上
  3.  *
  4.  * @param A 原柱子
  5.  * @param B 辅助柱子
  6.  * @param C 目标柱子
  7.  */
  8. public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
  9.     movePlate(A.size(), A, B, C);
  10. }
  12. private void movePlate(int num, List<Integer> original, List<Integer> auxiliary, List<Integer> target) {
  13.     if (num == 1) {    
  14.         // 只剩一个盘子时，直接移动即可
  15.         target.add(original.remove(original.size() - 1));
  16.         return;
  17.     }
  18.     // 将 size-1 个盘子，从 original 移动到 auxiliary
  19.     movePlate(num - 1, original, target, auxiliary);
  20.     // 将 第size个盘子，从 original 移动到 target
  21.     target.add(original.remove(original.size() - 1));
  22.     // 将 size-1 个盘子，从 auxiliary 移动到 target
  23.     movePlate(num - 1, auxiliary, original, target);   
  24. }