1.分治

1.1 【中等】Pow(x, n)（50）

image.png
递归

  1. /**
  2.  * 建议背这个
  3.  */
  4. public class MyPow {
  5.     public double myPow(double x, int n) {
  6.         long N = n;
  7.         // 根据N是否大于等于0进行分治
  8.         return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
  9.     }
  11.     public double quickMul(double x, long N) {
  12.         if (N == 0) {
  13.             return 1.0;
  14.         }
  15.         double y = quickMul(x, N / 2);
  16.         // 偶数直接/2平方即可，否则还要乘以x
  17.         return N % 2 == 0 ? y * y : y * y * x;
  18.     }
  19. }

非递归

  1. public class MyPow {
  2.     public double myPow(double x, int n) {
  3.         long N = n;
  4.         return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
  5.     }df 
  7.     public double quickMul(double x, long N) {
  8.         double ans = 1.0;
  9.         // 贡献的初始值为 x
  10.         double xContribute = x;
  11.         // 在对 N 进行二进制拆分的同时计算答案
  12.         while (N > 0) {
  13.             if (N % 2 == 1) {
  14.                 // 如果 N 二进制表示的最低位为 1，那么需要计入贡献
  15.                 ans *= xContribute;
  16.             }
  17.             // 将贡献不断地平方
  18.             xContribute *= xContribute;
  19.             // 舍弃 N 二进制表示的最低位，这样我们每次只要判断最低位即可
  20.             N /= 2;
  21.         }
  22.         return ans;
  23.     }
  24. }

2.回溯

2.1 【中等】子集（78）

image.png

  1. /**
  2.  * 回溯就是要递归，递归一次后移除元素，再进行一次递归
  3.  */
  4. public class Subsets {
  5.     List<Integer> t = new ArrayList<>();
  6.     List<List<Integer>> ans = new ArrayList<>();
  8.     public List<List<Integer>> subsets(int[] nums) {
  9.         dfs(0, nums);
  10.         return ans;
  11.     }
  13.     public void dfs(int cur, int[] nums) {
  14.         if (cur == nums.length) {
  15.             ans.add(new ArrayList<>(t));
  16.             return;
  17.         }
  18.         t.add(nums[cur]);
  19.         dfs(cur + 1, nums);
  20.         t.remove(t.size() - 1);
  21.         dfs(cur + 1, nums);
  22.     }
  23. }

2.2 【中等】电话号码的字母组合（17）

image.png

  1. /**
  2.  * 这个回溯在删除元素后不需要再进行一次递归，实战时可以都尝试一下
  3.  */
  4. class Solution {
  5.     public List<String> letterCombinations(String digits) {
  6.         List<String> combinations = new ArrayList<>();
  7.         if (digits.length() == 0) {
  8.             return combinations;
  9.         }
  10.         // 需要构建一个map
  11.         Map<Character, String> phoneMap = new HashMap<Character, String>() {{
  12.             put('2', "abc");
  13.             put('3', "def");
  14.             put('4', "ghi");
  15.             put('5', "jkl");
  16.             put('6', "mno");
  17.             put('7', "pqrs");
  18.             put('8', "tuv");
  19.             put('9', "wxyz");
  20.         }};
  21.         backtrack(combinations, phoneMap, digits, 0, new StringBuffer());
  22.         return combinations;
  23.     }
  25.     public void backtrack(List<String> combinations,Map<Character, String> phoneMap,String digits,Integer index,StringBuffer combination){
  26.         if(index==digits.length()){
  27.             combinations.add(combination.toString());
  28.         }else{
  29.             char digit = digits.charAt(index);
  30.             String letters = phoneMap.get(digit);
  31.             int lettersCount = letters.length();
  32.             for (int i = 0; i < lettersCount; i++) {
  33.                 combination.append(letters.charAt(i));
  34.                 backtrack(combinations,phoneMap,digits,index+1,combination);
  35.                 // 递归后删除元素
  36.                 combination.deleteCharAt(index);
  37.             }
  38.         }
  39.     }
  40. }

2.3 【困难】N 皇后（51）

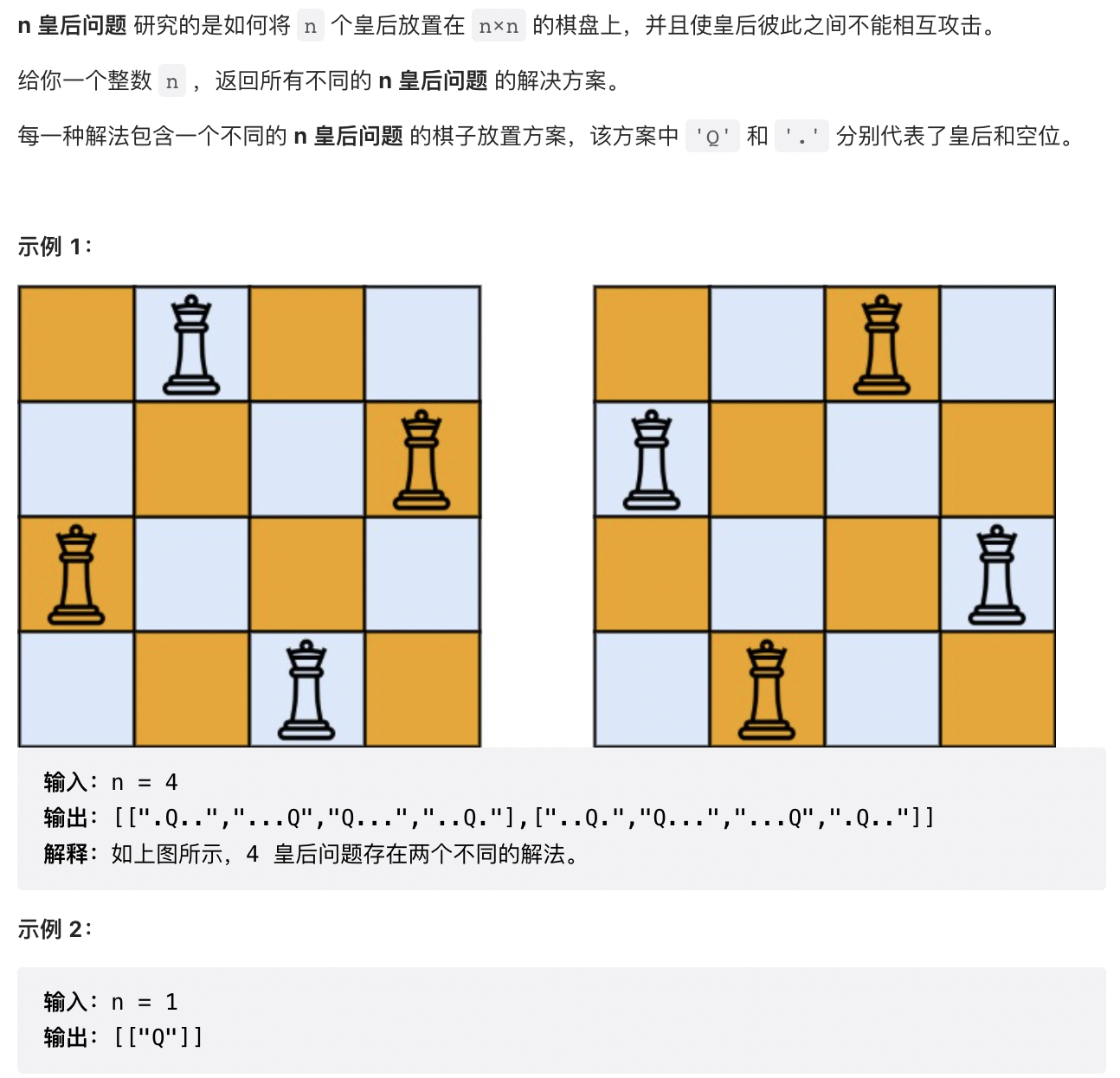
image.png

  1. /**
  2.  * 需要找出两条斜线与行列的关系，这边的话直接死记就行
  3.  */
  4. public class SolveNQueens {
  5.     public List<List<String>> solveNQueens(int n) {
  6.         List<List<String>> solutions = new ArrayList<>();
  7.         int[] queens = new int[n];
  8.         Arrays.fill(queens, -1);
  9.         Set<Integer> columns = new HashSet<>();
  10.         Set<Integer> diagonals1 = new HashSet<>();
  11.         Set<Integer> diagonals2 = new HashSet<>();
  12.         backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
  13.         return solutions;
  14.     }
  16.     public void backtrack(List<List<String>> solutions, int[] queens, int n, int row, Set<Integer> columns, Set<Integer> diagonals1, Set<Integer> diagonals2) {
  17.         if (row == n) {
  18.             List<String> board = generateBoard(queens, n);
  19.             solutions.add(board);
  20.         } else {
  21.             for (int i = 0; i < n; i++) {
  22.                 if (columns.contains(i)) {
  23.                     continue;
  24.                 }
  25.                 int diagonal1 = row - i;
  26.                 if (diagonals1.contains(diagonal1)) {
  27.                     continue;
  28.                 }
  29.                 int diagonal2 = row + i;
  30.                 if (diagonals2.contains(diagonal2)) {
  31.                     continue;
  32.                 }
  33.                 queens[row] = i;
  34.                 columns.add(i);
  35.                 diagonals1.add(diagonal1);
  36.                 diagonals2.add(diagonal2);
  37.                 backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
  38.                 queens[row] = -1;
  39.                 columns.remove(i);
  40.                 diagonals1.remove(diagonal1);
  41.                 diagonals2.remove(diagonal2);
  42.             }
  43.         }
  44.     }
  46.     public List<String> generateBoard(int[] queens, int n) {
  47.         List<String> board = new ArrayList<>();
  48.         for (int i = 0; i < n; i++) {
  49.             char[] row = new char[n];
  50.             Arrays.fill(row, '.');
  51.             row[queens[i]] = 'Q';
  52.             board.add(new String(row));
  53.         }
  54.         return board;
  55.     }
  56. }

2.4 【中等】迷宫问题（HJ43）

image.png
image.png
本题不好用动态规划，因为它可以上下左右移动，所以深搜是最好的，当i=row-1,j=column-1退出循环

  1. public class MinPath {
  2.     /**
  3.      * 所有可能路径
  4.      */
  5.     private static Stack<int[]> PATH = new Stack<>();
  7.     /**
  8.      * 最短路径
  9.      */
  10.     private static Stack<int[]> MIN_PATH = new Stack<>();
  12.     public static void main(String[] args) {
  13.         Scanner sc = new Scanner(System.in);
  14.         int row = sc.nextInt();
  15.         int column = sc.nextInt();
  16.         int[][] maze = new int[row][column];
  17.         for (int i = 0; i < row; i++) {
  18.             for (int j = 0; j < column; j++) {
  19.                 maze[i][j] = sc.nextInt();
  20.             }
  21.         }
  22.         dfs(maze, 0, 0, row, column);
  23.         while (!MIN_PATH.isEmpty()) {
  24.             int[] ints = MIN_PATH.pop();
  25.             System.out.println("(" + ints[0] + "," + ints[1] + ")");
  26.         }
  27.     }
  29.     private static void dfs(int[][] maze, int i, int j, int row, int column) {
  30.         if (i < 0 || i >= row || j < 0 || j >= column || maze[i][j] == 1) {
  31.             return;
  32.         }
  33.         PATH.push(new int[]{i, j});
  34.         if (i == row - 1 && j == column - 1) {
  35.             if (MIN_PATH.isEmpty() || PATH.size() < MIN_PATH.size()) {
  36.                 for (int k = PATH.size() - 1; k >= 0; k--) {
  37.                     MIN_PATH.push(PATH.get(k));
  38.                 }
  39.             }
  40.         }
  41.         maze[i][j] = 1;
  42.         dfs(maze, i - 1, j, row, column);
  43.         dfs(maze, i + 1, j, row, column);
  44.         dfs(maze, i, j - 1, row, column);
  45.         dfs(maze, i, j + 1, row, column);
  46.         maze[i][j] = 0;
  47.         PATH.pop();
  48.     }
  49. }

2.5 【中等】全排列（46）

image.png

  1. /**
  2.  * 需要交换位置，建议死记
  3.  */
  4. public class Permute {
  5.     List<List<Integer>> result = new ArrayList<>();
  7.     public List<List<Integer>> permute(int[] nums) {
  8.         List<Integer> list = new ArrayList<>();
  9.         for (int num : nums) {
  10.             list.add(num);
  11.         }
  12.         dfs(nums, 0, list);
  13.         return result;
  14.     }
  16.     public void dfs(int[] nums, int first, List<Integer> cur) {
  17.         if (first == nums.length) {
  18.             result.add(new ArrayList<>(cur));
  19.             return;
  20.         }
  21.         for (int i = first; i < nums.length; i++) {
  22.             // 动态维护数组
  23.             Collections.swap(cur, first, i);
  24.             // 继续递归填下一个数
  25.             dfs(nums, first + 1, cur);
  26.             // 撤销操作
  27.             Collections.swap(cur, first, i);
  28.         }
  29.     }
  30. }

2.6 【困难】24 点游戏（679）

image.png

  1. class Solution {
  2.     //回溯枚举 + 部分剪枝优化
  3.     static final int TARGET = 24;
  4.     //误差
  5.     static final double EPSILON = 1e-6;
  6.     //加、乘、减、除
  7.     static final int ADD = 0, MULTIPLY = 1, SUBTRACT = 2, DIVIDE = 3;
  9.     public boolean judgePoint24(int[] nums) {
  10.         //4个数入list
  11.         List<Double> list = new ArrayList<Double>();
  12.         for (int num : nums) {
  13.             list.add((double) num);
  14.         }
  15.         return solve(list);
  16.     }
  18.     public boolean solve(List<Double> list) {
  19.         if (list.size() == 0) {
  20.             return false;
  21.         }
  22.         //算完后只剩一个数，即结果，误差在可接受范围内判true
  23.         if (list.size() == 1) {
  24.             return Math.abs(list.get(0) - TARGET) < EPSILON;
  25.         }
  26.         int size = list.size();
  27.         //list里挑出一个数
  28.         for (int i = 0; i < size; i++) {
  29.             //再挑一个，做运算
  30.             for (int j = 0; j < size; j++) {
  31.                 //不能挑一样的
  32.                 if (i != j) {
  33.                     //没被挑到的扔进list2
  34.                     List<Double> list2 = new ArrayList<Double>();
  35.                     for (int k = 0; k < size; k++) {
  36.                         if (k != i && k != j) {
  37.                             list2.add(list.get(k));
  38.                         }
  39.                     }
  40.                     //四种运算挑一个，算完的结果加到list2里做第三个数
  41.                     for (int k = 0; k < 4; k++) {
  42.                         //k < 2是指，所挑运算为加或乘
  43.                         //i > j是为了判定交换律的成立，如果i < j,说明是第一次做加或乘运算
  44.                         //eg: i = 0, j = 1, k = 1 → 挑第一个和第二个数，两数相乘
  45.                         //    i = 1, j = 0, k = 1 → 挑第二个和第一个数，两数相乘  →  无效的重复计算
  46.                         if (k < 2 && i > j) {
  47.                             continue;
  48.                         }
  49.                         //加
  50.                         if (k == ADD) {
  51.                             list2.add(list.get(i) + list.get(j));
  52.                             //乘
  53.                         } else if (k == MULTIPLY) {
  54.                             list2.add(list.get(i) * list.get(j));
  55.                             //减
  56.                         } else if (k == SUBTRACT) {
  57.                             list2.add(list.get(i) - list.get(j));
  58.                             //除
  59.                         } else if (k == DIVIDE) {
  60.                             //如果除数等于0，直接判这次所挑选的运算为false，跳出此次循环
  61.                             if (Math.abs(list.get(j)) < EPSILON) {
  62.                                 continue;
  63.                             } else {
  64.                                 list2.add(list.get(i) / list.get(j));
  65.                             }
  66.                         }
  67.                         //至此已经由4→3，进入下一层由3→2的过程，依次类推
  68.                         if (solve(list2)) {
  69.                             return true;
  70.                         }
  71.                         //没凑成24就把加到list2末尾的结果数删掉，考虑下种运算可能
  72.                         list2.remove(list2.size() - 1);
  73.                     }
  74.                 }
  75.             }
  76.         }
  77.         return false;
  78.     }
  79. }