1. 贪心

2.二分查找

2.1 【简单】x 的平方根 （69）

image.png

  1. /**
  2.  * 二分法
  3.  */
  4. public int mySqrt(int x) {
  5.     int l = 0, r = x, ans = -1;
  6.     while (l <= r) {
  7.         int mid = l + (r - l) / 2;
  8.         if ((long) mid * mid <= x) {
  9.             ans = mid;
  10.             l = mid + 1;
  11.         } else {
  12.             r = mid - 1;
  13.         }
  14.     }
  15.     return ans;
  16. }

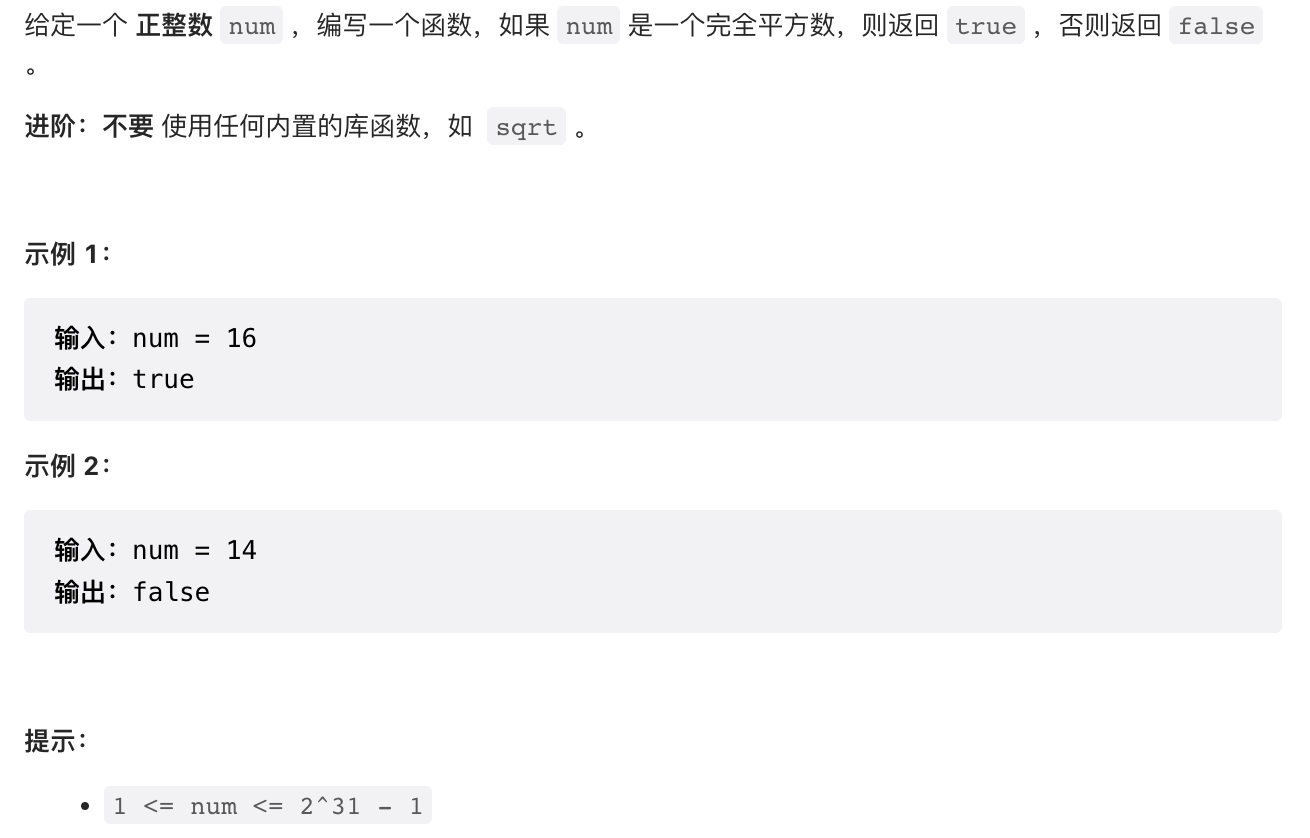
2.2 【简单】有效的完全平方数 （367）

image.png

  1. /**
  2.  * 二分法
  3.  */
  4. public boolean isPerfectSquare(int num) {
  5.     int l = 0, r = num;
  6.     while (l <= r) {
  7.         int mid = l + (r - l) / 2;
  8.         if ((long) mid * mid < num) {
  9.             l = mid + 1;
  10.         } else if ((long) mid * mid > num) {
  11.             r = mid - 1;
  12.         } else {
  13.             return true;
  14.         }
  15.     }
  16.     return false;
  17. }

2.3 【中等】搜索旋转排序数组 （33）

image.png

  1. /**
  2.  * 首元素与中间元素进行比较，分类讨论
  3.  */
  4. public int search(int[] nums, int target) {
  5.     int n = nums.length;
  6.     if (n == 0) {
  7.         return -1;
  8.     }
  9.     if (n == 1) {
  10.         return nums[0] == target ? 0 : -1;
  11.     }
  12.     int l = 0, r = n - 1;
  13.     while (l <= r) {
  14.         int mid = (l + r) / 2;
  15.         if (nums[mid] == target) {
  16.             return mid;
  17.         }
  18.         // 中位数先和0元素比较
  19.         if (nums[0] <= nums[mid]) {
  20.             // 4,5,6,7,0,1,2,3
  21.             if (nums[0] <= target && target < nums[mid]) {
  22.                 r = mid - 1;
  23.             } else {
  24.                 l = mid + 1;
  25.             }
  26.         } else {
  27.             // 6,7,0,1,2,3,4,5
  28.             if (nums[mid] < target && target <= nums[n - 1]) {
  29.                 l = mid + 1;
  30.             } else {
  31.                 r = mid - 1;
  32.             }
  33.         }
  34.     }
  35.     return -1;
  36. }

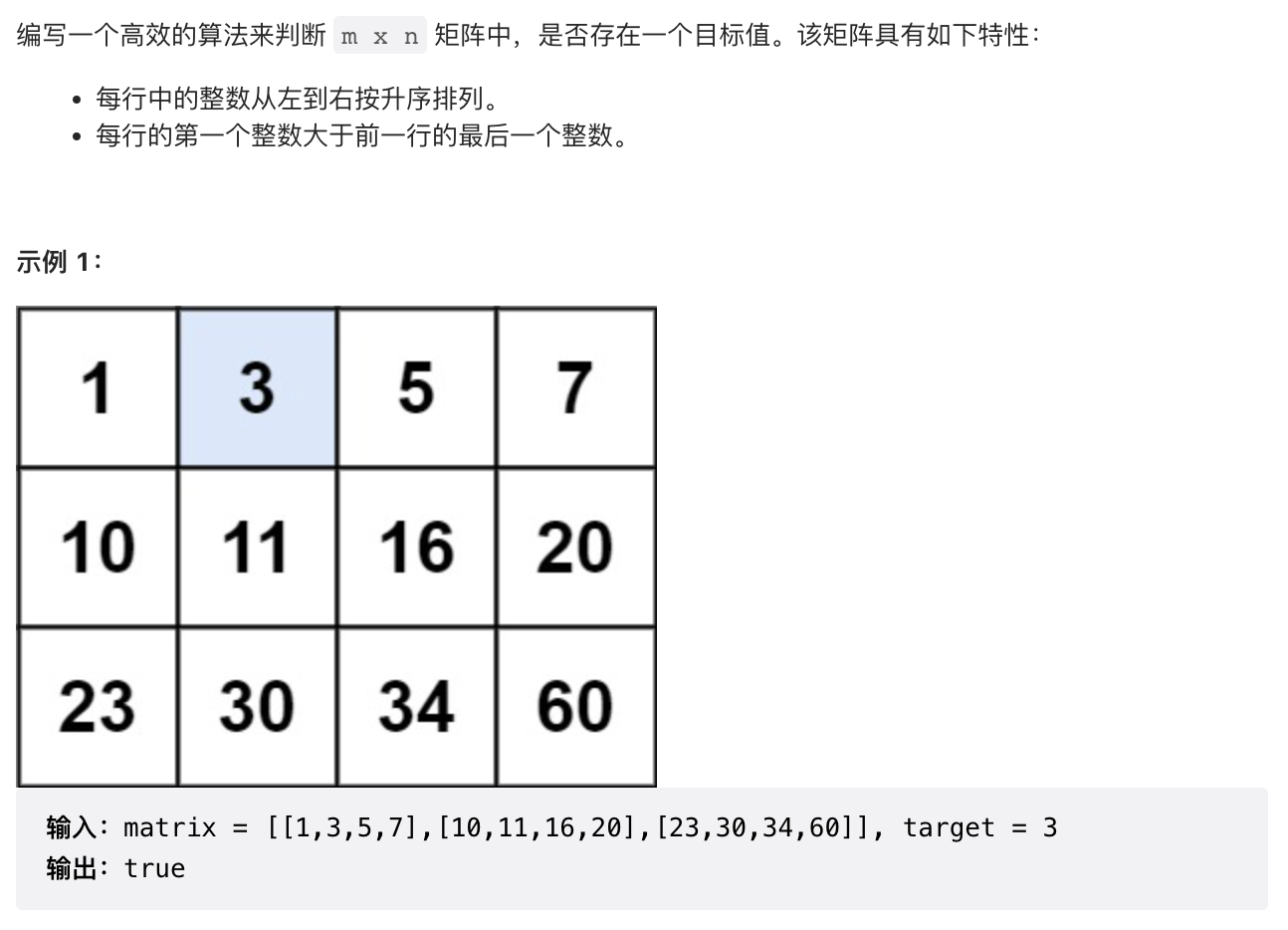
2.4 【中等】搜索二维矩阵 （74）

image.png

  1. /**
  2.  * 二分法
  3.  */
  4. public boolean searchMatrix(int[][] matrix, int target) {
  5.     int m = matrix.length, n = matrix[0].length;
  6.     int low = 0, high = m * n - 1;
  7.     while (low <= high) {
  8.         int mid = (high - low) / 2 + low;
  9.         int x = matrix[mid / n][mid % n];
  10.         if (x < target) {
  11.             low = mid + 1;
  12.         } else if (x > target) {
  13.             high = mid - 1;
  14.         } else {
  15.             return true;
  16.         }
  17.     }
  18.     return false;
  19. }

2.5 【中等】寻找旋转排序数组中的最小值 （153）

image.png

  1. /**
  2.  * 与一般二分法不同，需要仔细观察记忆。
  3.  */
  4. public int findMin(int[] nums) {
  5.     int low = 0;
  6.     int high = nums.length - 1;
  7.     // 没有等号
  8.     while (low < high) {
  9.         int pivot = low + (high - low) / 2;
  10.         if (nums[pivot] < nums[high]) {
  11.             // 不为pivot-1
  12.             high = pivot;
  13.         } else {
  14.             low = pivot + 1;
  15.         }
  16.     }
  17.     return nums[low];
  18. }