1.DFS

1.1 【中等】最小基因变化（433）

/**
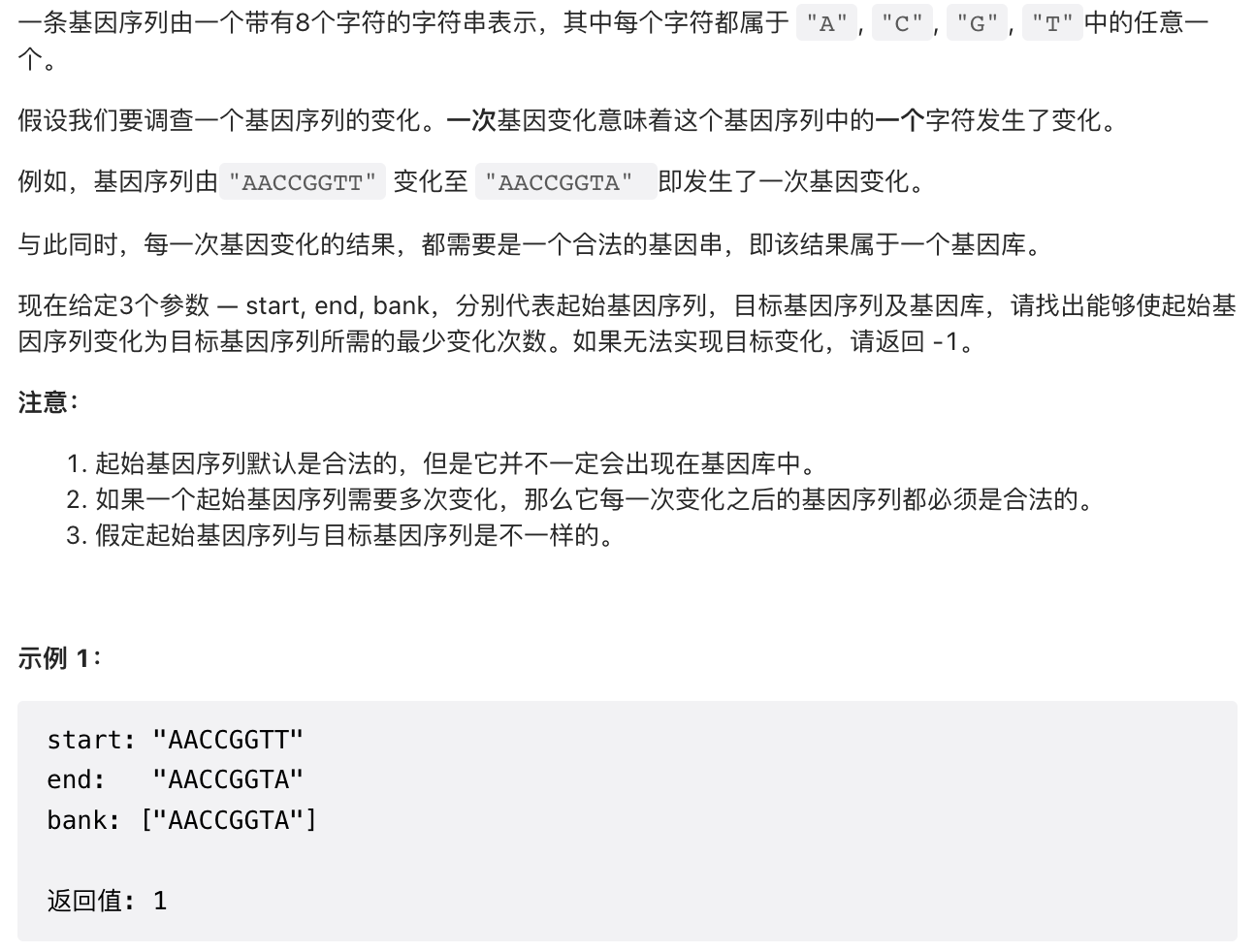
 * 其实还是回溯法
 */
public class MinMutation {
    int minStepCount = Integer.MAX_VALUE;
    public int minMutation(String start, String end, String[] bank) {
        dfs(new HashSet<>(), 0, start, end, bank);
        return (minStepCount == Integer.MAX_VALUE) ? -1 : minStepCount;
    }
    private void dfs(HashSet<String> step, int stepCount,
                     String current, String end, String[] bank) {
        if (stepCount > minStepCount) {
            // 当前步骤大于最小次数直接返回
            return;
        }
        if (current.equals(end)) {
            // 判断是否是最少次
            minStepCount = Math.min(stepCount, minStepCount);
        }
        for (String str : bank) {
            int diff = 0;
            // 寻找与基因库不同的字符数
            for (int i = 0; i < str.length(); i++) {
                if (current.charAt(i) != str.charAt(i)) {
                    if (++diff > 1) {
                        break;
                    }
                }
            }
            if (diff == 1 && !step.contains(str)) {
                // 回溯
                step.add(str);
                dfs(step, stepCount + 1, str, end, bank);
                step.remove(str);
            }
        }
    }
}

1.2 【中等】在每个树行中找最大值（515）

/**
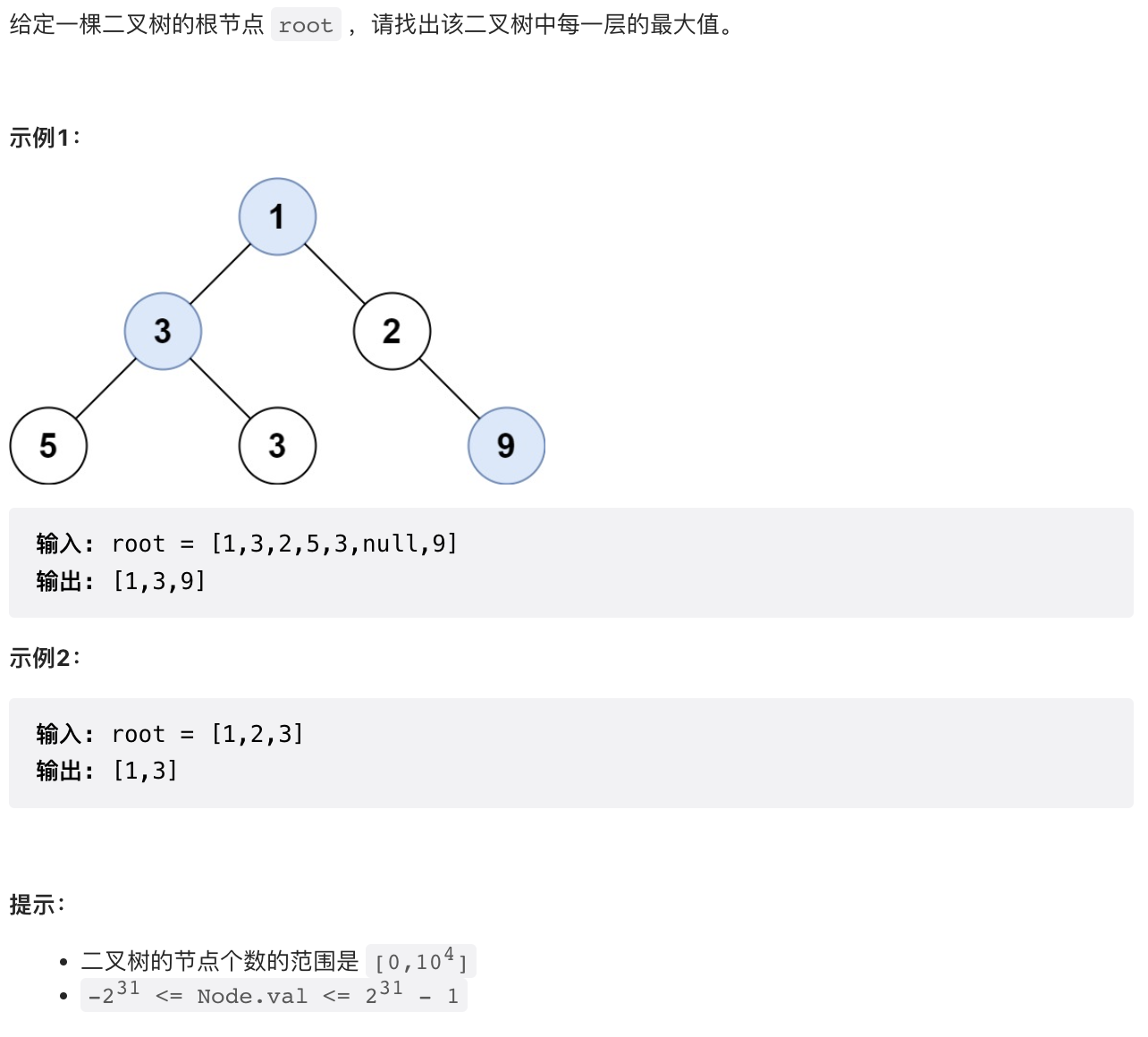
 * 此题不是回溯法，但是用到了list的一些骚操作
 */
public class LargestValues {
    /**
     * 保存对应层数的最大值，第一层的最大值在索引为0处，第二层在1处
     */
    private List<Integer> list = new ArrayList<>();
    public List<Integer> largestValues(TreeNode root) {
        dfs(root, 1);
        return list;
    }
    private void dfs(TreeNode node, int depth) {
        if (node == null) {
            return;
        }
        //如果当前层数还没有添加过值，就默认当前值是当前层数最大的值
        //如果当前层已经有最大值，就取出当前层最大值和当前值比较，如果当前值更大就更新对应层数的最大值
        if (depth > list.size()) {
            list.add(node.value);
        } else {
            if (node.value >= list.get(depth - 1)) {
                list.set(depth - 1, node.value);
            }
        }
        //继续递归左右子树
        dfs(node.left, depth + 1);
        dfs(node.right, depth + 1);
    }
}

2.BFS

2.1 【中等】二叉树的层序遍历（102）

2.2 【中等】最小基因变化（433）

2.3 【中等】括号生成（22）

2.4 【中等】在每个树行中找最大值（515）

2.5 【中等】 二叉树的锯齿形层序遍历（103）

/**
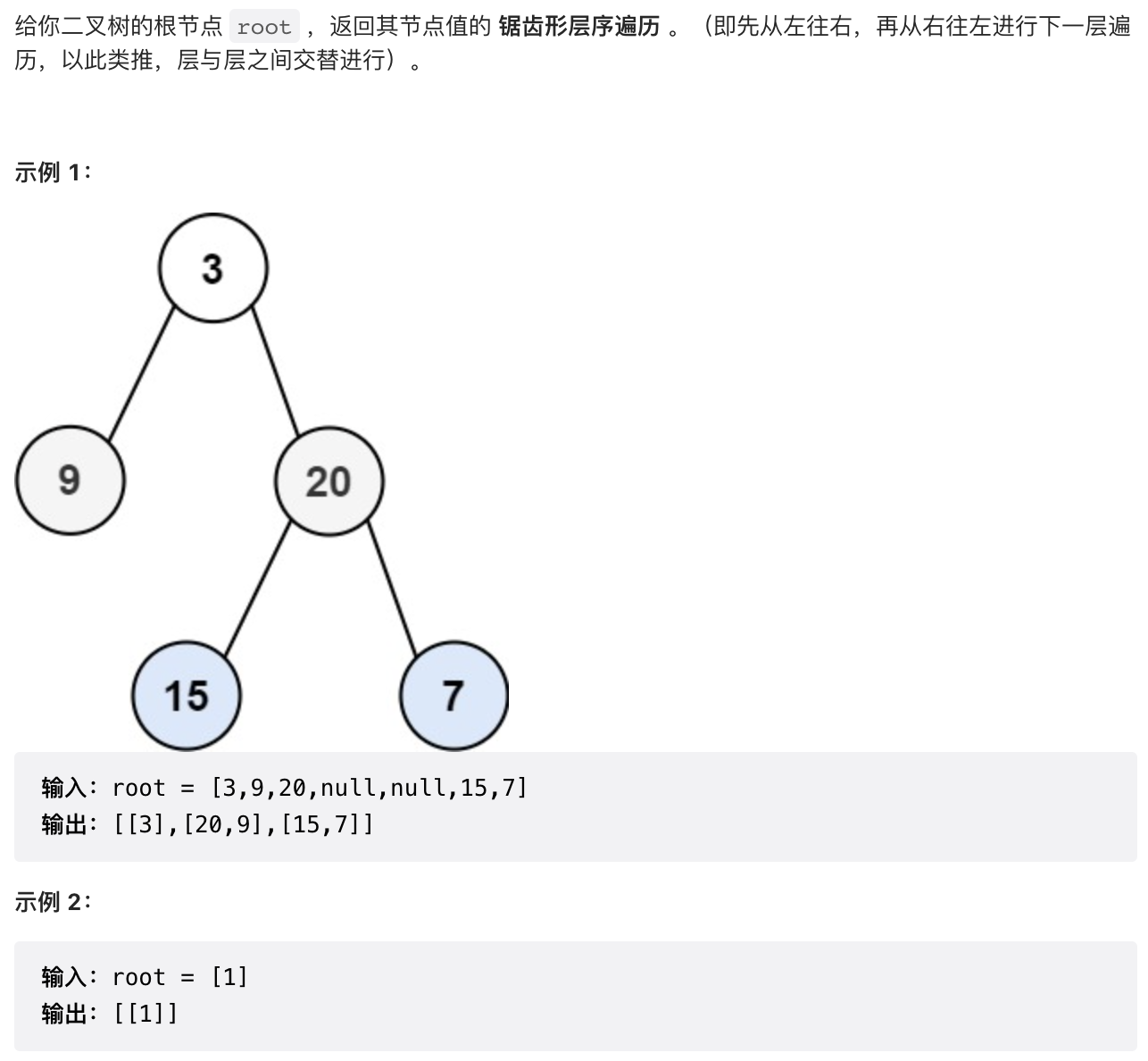
 * 和层序遍历相同，不过需要加一个判断条件，以决定是在头部添加还是尾部添加
 */
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
    List<List<Integer>> ans = new LinkedList<>();
    if (root == null) {
        return ans;
    }
    Queue<TreeNode> nodeQueue = new LinkedList<>();
    nodeQueue.offer(root);
    boolean isOrderLeft = true;
    while (!nodeQueue.isEmpty()) {
        Deque<Integer> levelList = new LinkedList<>();
        // 这边一定要单独写个size，不然会在循环中改变长度，不符合预期
        int size = nodeQueue.size();
        for (int i = 0; i < size; ++i) {
            TreeNode curNode = nodeQueue.poll();
            if (isOrderLeft) {
                levelList.offerLast(curNode.value);
            } else {
                levelList.offerFirst(curNode.value);
            }
            if (curNode.left != null) {
                nodeQueue.offer(curNode.left);
            }
            if (curNode.right != null) {
                nodeQueue.offer(curNode.right);
            }
        }
        ans.add(new LinkedList<>(levelList));
        isOrderLeft = !isOrderLeft;
    }
    return ans;
}

2.6 【中等】 岛屿数量（200）

bfs

/**
 * bfs
 */
public int numIslands(char[][] grid) {
    if (grid == null || grid.length == 0) {
        return 0;
    }
    int nr = grid.length;
    int nc = grid[0].length;
    int numIslands = 0;
    for (int r = 0; r < nr; ++r) {
        for (int c = 0; c < nc; ++c) {
            if (grid[r][c] == '1') {
                ++numIslands;
                grid[r][c] = '0';
                // bfs
                Queue<Integer> neighbors = new LinkedList<>();
                neighbors.add(r * nc + c);
                while (!neighbors.isEmpty()) {
                    // 将上下左右如果是1都置为0
                    int id = neighbors.remove();
                    int row = id / nc;
                    int col = id % nc;
                    if (row - 1 >= 0 && grid[row - 1][col] == '1') {
                        neighbors.add((row - 1) * nc + col);
                        grid[row - 1][col] = '0';
                    }
                    if (row + 1 < nr && grid[row + 1][col] == '1') {
                        neighbors.add((row + 1) * nc + col);
                        grid[row + 1][col] = '0';
                    }
                    if (col - 1 >= 0 && grid[row][col - 1] == '1') {
                        neighbors.add(row * nc + col - 1);
                        grid[row][col - 1] = '0';
                    }
                    if (col + 1 < nc && grid[row][col + 1] == '1') {
                        neighbors.add(row * nc + col + 1);
                        grid[row][col + 1] = '0';
                    }
                }
            }
        }
    }
    return numIslands;
}

dfs

/**
 * dfs 核心思想还是将是1的上下左右置为0
 */
class Solution {
    void dfs(char[][] grid, int r, int c) {
        int nr = grid.length;
        int nc = grid[0].length;
        if (r < 0 || c < 0 || r >= nr || c >= nc || grid[r][c] == '0') {
            return;
        }
        grid[r][c] = '0';
        dfs(grid, r - 1, c);
        dfs(grid, r + 1, c);
        dfs(grid, r, c - 1);
        dfs(grid, r, c + 1);
    }
    public int numIslands(char[][] grid) {
        if (grid == null || grid.length == 0) {
            return 0;
        }
        int nr = grid.length;
        int nc = grid[0].length;
        int num_islands = 0;
        for (int r = 0; r < nr; ++r) {
            for (int c = 0; c < nc; ++c) {
                if (grid[r][c] == '1') {
                    ++num_islands;
                    dfs(grid, r, c);
                }
            }
        }
        return num_islands;
    }
}