1【简单】剑指 Offer 10- I. 斐波那契数列

image.png

  1. /*
  2.  * 动态规划，2开始，取模1e9+7
  3.  */
  4. public int fib(int n) {
  5.     final int MOD = 1000000007;
  6.     if (n < 2) {
  7.         return n;
  8.     }
  9.     int p = 0, q = 0, r = 1;
  10.     for (int i = 2; i <= n; ++i) {
  11.         p = q;
  12.         q = r;
  13.         r = (p + q) % MOD;
  14.     }
  15.     return r;
  16. }

2【困难】最长有效括号（32）

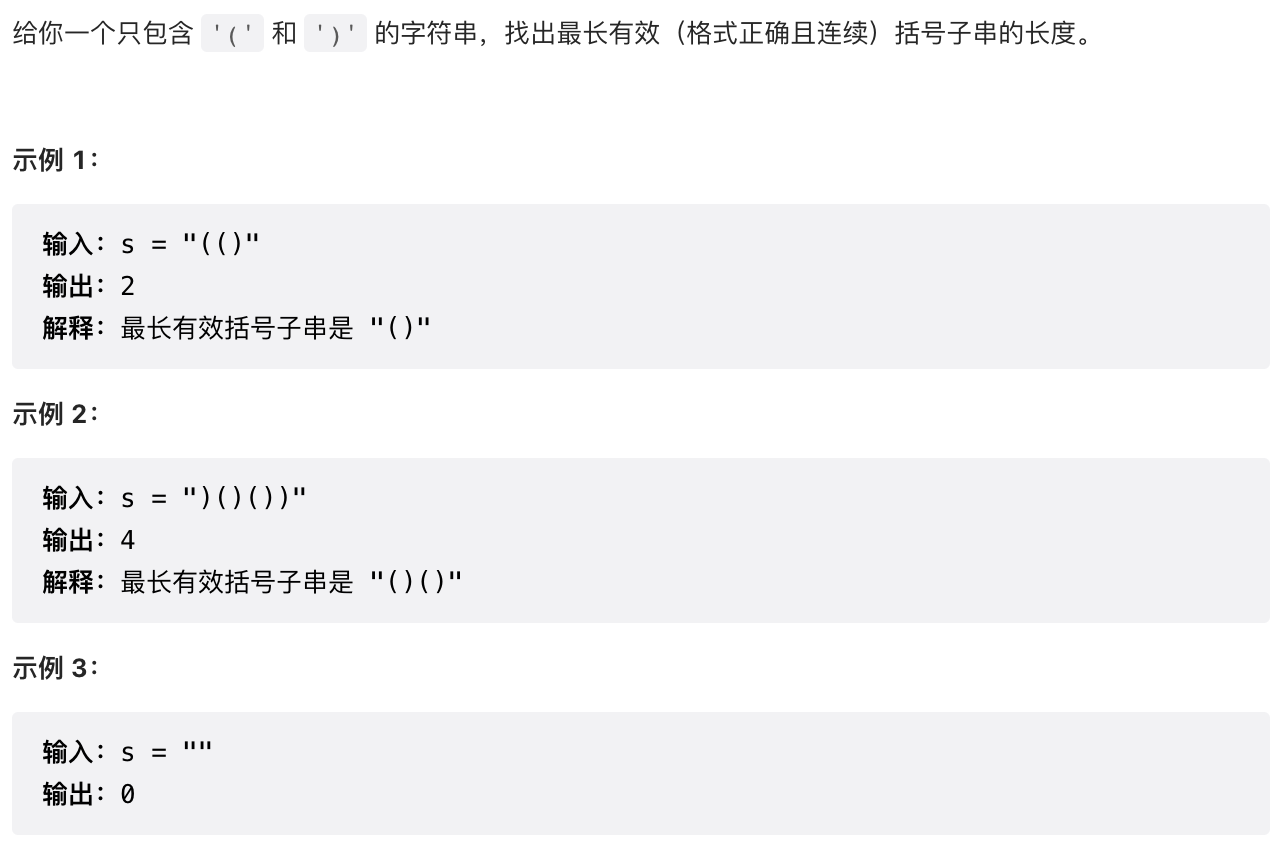
image.png
image.png

  1. /*
  2.  * 分两种情况，一种前一个元素为(，一种前一种元素为)
  3.  */
  4. public int longestValidParentheses(String s) {
  5.     int maxans = 0;
  6.     int[] dp = new int[s.length()];
  7.     for (int i = 1; i < s.length(); i++) {
  8.         if (s.charAt(i) == ')') {
  9.             if (s.charAt(i - 1) == '(') {
  10.                 dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
  11.             } else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
  12.                 dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
  13.             }
  14.             maxans = Math.max(maxans, dp[i]);
  15.         }
  16.     }
  17.     return maxans;
  18. }

3【中等】跳跃游戏（55）

image.png

  1. /*
  2.  * 每个位置都有个最远处的映射，只要当前最远处能映射到终点就可以了
  3.  */
  4. public boolean canJump(int[] nums) {
  5.     // 能跑到最远处下标
  6.     int maxPos = nums[0];
  7.     for (int i = 1; i < nums.length; ++i) {
  8.         if (i > maxPos) {
  9.             // 跑不到
  10.             return false;
  11.         }
  12.         // 不断求得最远处的下标
  13.         maxPos = Math.max(i + nums[i], maxPos);
  14.     }
  15.     return true;
  16. }

4【中等】跳跃游戏 II（45）
image.png

动态规划

  1. /*
  2.  * 动态规划，dp[i]=Math.min(dp[i],dp[j]+1)
  3.  */
  4. public int jump(int[] nums) {
  5.     long[] dp = new long[nums.length];
  6.     Arrays.fill(dp, Integer.MAX_VALUE);
  7.     dp[0] = 0;
  8.     for (int i = 1; i < nums.length; i++) {
  9.         // j代表到达i的前一步，所以是+1
  10.         for (int j = 0; j < nums.length; j++) {
  11.             if (nums[j] + j >= i) {
  12.                 dp[i] = Math.min(dp[i], dp[j] + 1);
  13.             }
  14.         }
  15.     }
  16.     return dp[nums.length - 1] == Integer.MAX_VALUE ? 0 : (int) dp[nums.length - 1];
  17. }

贪心

  1. /*
  2.  * 假设每次都能到达最远位置
  3.  */
  4. public int jump(int[] nums) {
  5.     int length = nums.length;
  6.     int end = 0;
  7.     int maxPosition = 0;
  8.     int steps = 0;
  9.     for (int i = 0; i < length - 1; i++) {
  10.         maxPosition = Math.max(maxPosition, i + nums[i]);
  11.         if (i == end) {
  12.             end = maxPosition;
  13.             steps++;
  14.         }
  15.     }
  16.     return steps;
  17. }

5【简单】最大子数组和（53）

image.png

  1. /*
  2.  * f(i)=Max(f(i-1)+nums[i],nums[i])
  3.  */
  4. public int maxSubArray(int[] nums) {
  5.     int pre = 0, maxAns = nums[0];
  6.     for (int x : nums) {
  7.         pre = Math.max(pre + x, x);
  8.         maxAns = Math.max(maxAns, pre);
  9.     }
  10.     return maxAns;
  11. }

6【中等】不同路径（62）

image.png

  1. /*
  2.  * f(i,j)=f(i-1,j)+f(i,j-1)
  3.  */
  4. public int uniquePaths(int m, int n) {
  5.     int[][] f = new int[m][n];
  6.     for (int i = 0; i < m; ++i) {
  7.         f[i][0] = 1;
  8.     }
  9.     for (int j = 0; j < n; ++j) {
  10.         f[0][j] = 1;
  11.     }
  12.     for (int i = 1; i < m; ++i) {
  13.         for (int j = 1; j < n; ++j) {
  14.             f[i][j] = f[i - 1][j] + f[i][j - 1];
  15.         }
  16.     }
  17.     return f[m - 1][n - 1];
  18. }

7【中等】不同路径2（63）

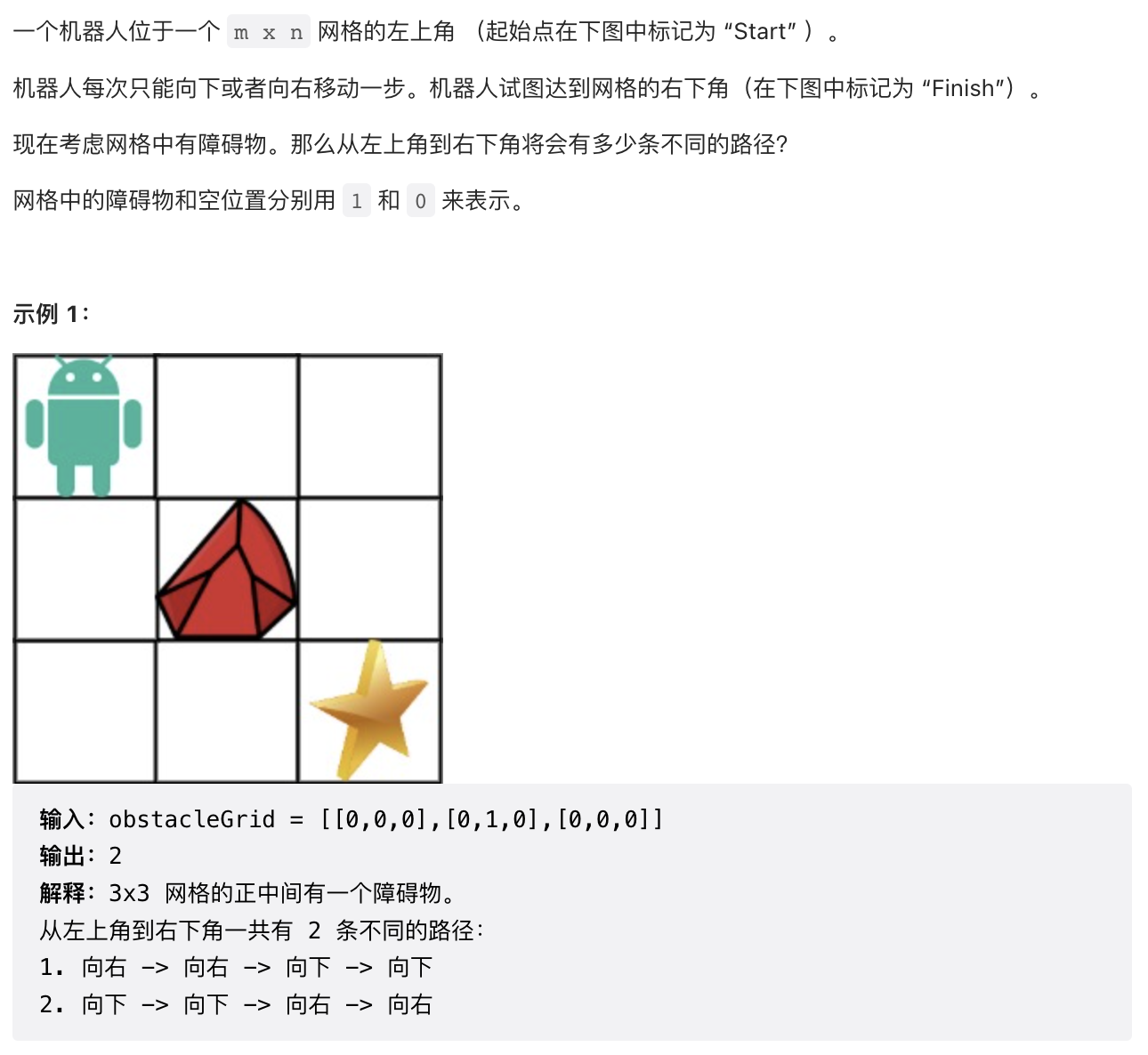
image.png

  1. /*
  2.  * f(i,j)=f(i-1,j)+f(i,j-1)||0
  3.  * 本题压缩为1维数组，难以理解，用上提的二维数组一样可以解决
  4.  */
  5. public int uniquePathsWithObstacles(int[][] obstacleGrid) {
  6.     int n = obstacleGrid.length, m = obstacleGrid[0].length;
  7.     int[] f = new int[m];
  8.     f[0] = obstacleGrid[0][0] == 0 ? 1 : 0;
  9.     for (int i = 0; i < n; ++i) {
  10.         for (int j = 0; j < m; ++j) {
  11.             if (obstacleGrid[i][j] == 1) {
  12.                 f[j] = 0;
  13.                 continue;
  14.             }
  15.             if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
  16.                 f[j] += f[j - 1];
  17.             }
  18.         }
  19.     }
  20.     return f[m - 1];
  21. }

8【中等】最小路径和（64）

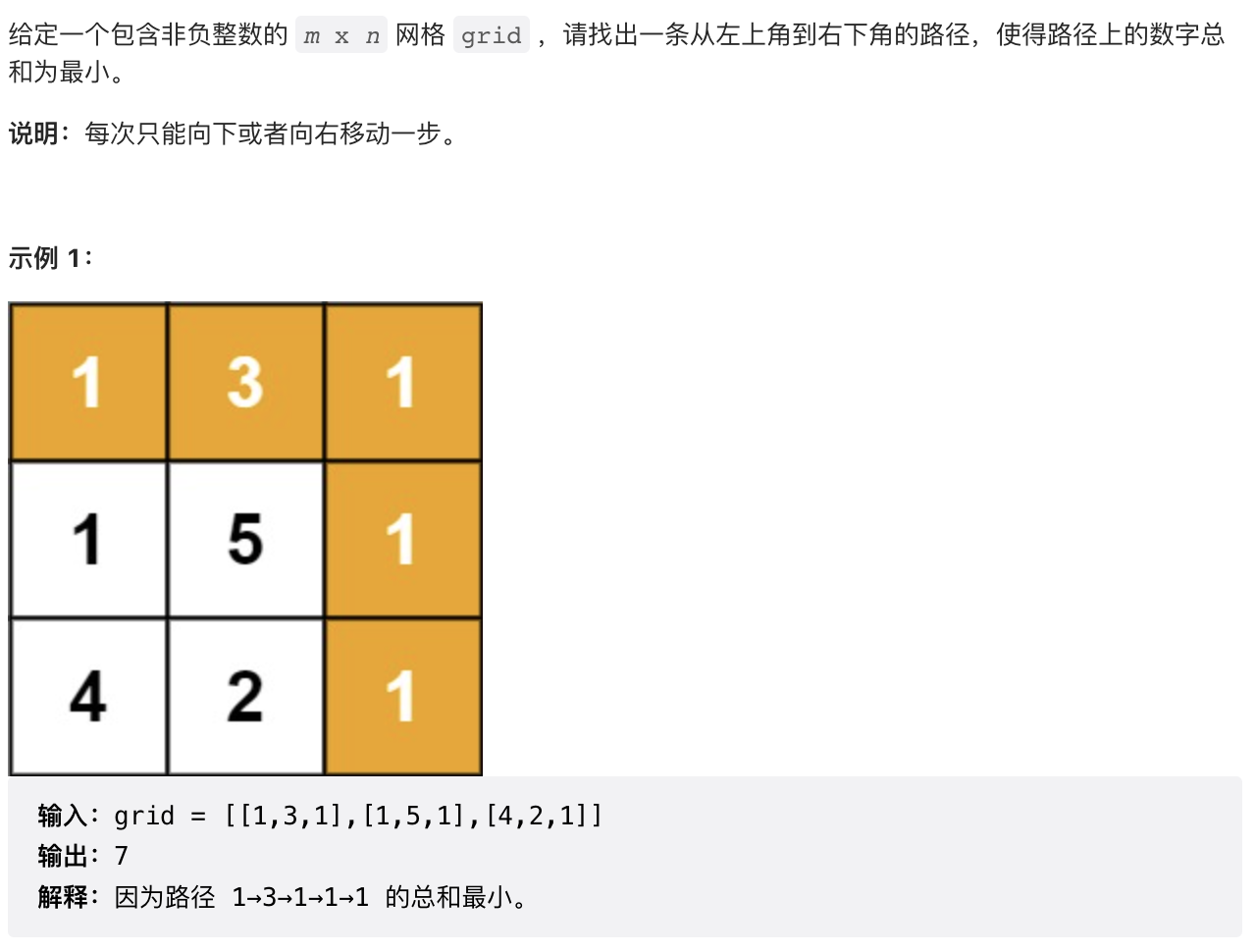
image.png

  1. /*
  2.  * f(i,j)=Min(f(i-1,j)+f(i,j-1))+grid[i][j]
  3.  */
  4. public int minPathSum(int[][] grid) {
  5.     if (grid == null || grid.length == 0 || grid[0].length == 0) {
  6.         return 0;
  7.     }
  8.     int rows = grid.length, columns = grid[0].length;
  9.     int[][] dp = new int[rows][columns];
  10.     dp[0][0] = grid[0][0];
  11.     for (int i = 1; i < rows; i++) {
  12.         dp[i][0] = dp[i - 1][0] + grid[i][0];
  13.     }
  14.     for (int j = 1; j < columns; j++) {
  15.         dp[0][j] = dp[0][j - 1] + grid[0][j];
  16.     }
  17.     for (int i = 1; i < rows; i++) {
  18.         for (int j = 1; j < columns; j++) {
  19.             dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
  20.         }
  21.     }
  22.     return dp[rows - 1][columns - 1];
  23. }

9【中等】一和零（474）

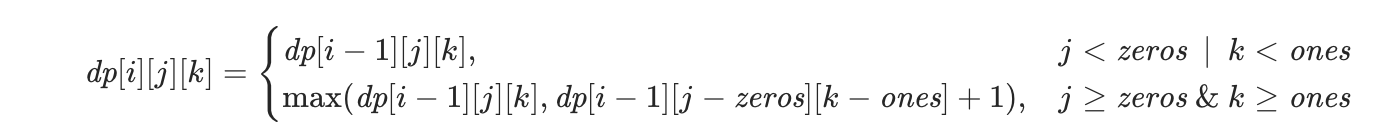
image.png
image.png

  1. public class FindMaxForm {
  2.     public int findMaxForm(String[] strs, int m, int n) {
  3.         int[][] dp = new int[m + 1][n + 1];
  4.         int length = strs.length;
  5.         for (int i = 0; i < length; i++) {
  6.             int[] zerosOnes = getZerosOnes(strs[i]);
  7.             int zeros = zerosOnes[0], ones = zerosOnes[1];
  8.             for (int j = m; j >= zeros; j--) {
  9.                 for (int k = n; k >= ones; k--) {
  10.                     dp[j][k] = Math.max(dp[j][k], dp[j - zeros][k - ones] + 1);
  11.                 }
  12.             }
  13.         }
  14.         return dp[m][n];
  15.     }
  17.     public int[] getZerosOnes(String str) {
  18.         int[] zerosOnes = new int[2];
  19.         int length = str.length();
  20.         for (int i = 0; i < length; i++) {
  21.             zerosOnes[str.charAt(i) - '0']++;
  22.         }
  23.         return zerosOnes;
  24.     }
  25. }

10【中等】目标和（494）

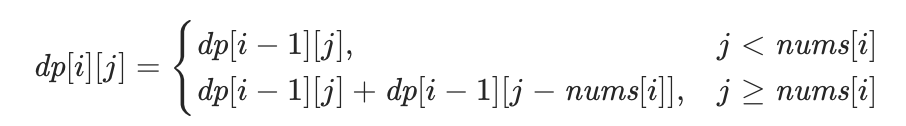
image.png
image.png

  1. public int findTargetSumWays(int[] nums, int target) {
  2.     int sum = 0;
  3.     for (int num : nums) {
  4.         sum += num;
  5.     }
  6.     int diff = sum - target;
  7.     if (diff < 0 || diff % 2 != 0) {
  8.         return 0;
  9.     }
  10.     int neg = diff / 2;
  11.     int[] dp = new int[neg + 1];
  12.     dp[0] = 1;
  13.     for (int num : nums) {
  14.         for (int j = neg; j >= num; j--) {
  15.             dp[j] += dp[j - num];
  16.         }
  17.     }
  18.     return dp[neg];
  19. }

11【中等】零钱兑换（322）

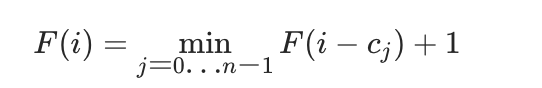
image.png
image.png

  1. public int coinChange(int[] coins, int amount) {
  2.     int max = amount + 1;
  3.     int[] dp = new int[amount + 1];
  4.     Arrays.fill(dp, max);
  5.     dp[0] = 0;
  6.     for (int i = 1; i <= amount; i++) {
  7.         for (int j = 0; j < coins.length; j++) {
  8.             if (coins[j] <= i) {
  9.                 dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
  10.             }
  11.         }
  12.     }
  13.     return dp[amount] > amount ? -1 : dp[amount];
  14. }

12【中等】零钱兑换 II（518）

image.png

  1. public static int change(int amount, int[] coins) {
  2.     int[] dp = new int[amount + 1];
  3.     dp[0] = 1;
  4.     for (int coin : coins) {
  5.         for (int i = coin; i <= amount; i++) {
  6.             dp[i] += dp[i - coin];
  7.         }
  8.     }
  9.     return dp[amount];
  10. }

13【中等】最长回文子串（5）

image.png

  1. /*
  2.  * 先枚举子串长度，再从左到右遍历
  3.  */
  4. public String longestPalindrome(String s) {
  5.     int len = s.length();
  6.     if (len < 2) {
  7.         return s;
  8.     }
  9.     int maxLen = 1;
  10.     int begin = 0;
  11.     // dp[i][j] 表示 s[i..j] 是否是回文串
  12.     boolean[][] dp = new boolean[len][len];
  13.     // 初始化：所有长度为 1 的子串都是回文串
  14.     for (int i = 0; i < len; i++) {
  15.         dp[i][i] = true;
  16.     }
  17.     char[] charArray = s.toCharArray();
  18.     // 递推开始
  19.     // 先枚举子串长度
  20.     for (int L = 2; L <= len; L++) {
  21.         // 枚举左边界，左边界的上限设置可以宽松一些
  22.         for (int i = 0; i < len; i++) {
  23.             // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
  24.             int j = L + i - 1;
  25.             // 如果右边界越界，就可以退出当前循环
  26.             if (j >= len) {
  27.                 break;
  28.             }
  29.             if (charArray[i] != charArray[j]) {
  30.                 dp[i][j] = false;
  31.             } else {
  32.                 if (j - i < 3) {
  33.                     dp[i][j] = true;
  34.                 } else {
  35.                     dp[i][j] = dp[i + 1][j - 1];
  36.                 }
  37.             }
  38.             // 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
  39.             if (dp[i][j] && j - i + 1 > maxLen) {
  40.                 maxLen = j - i + 1;
  41.                 begin = i;
  42.             }
  43.         }
  44.     }
  45.     return s.substring(begin, begin + maxLen);
  46. }

14【中等】买卖股票的最佳时机 II（122）

image.png
定义状态dp[i][0] 表示第 i 天交易完后手里没有股票的最大利润，dp[i][1] 表示第 i 天交易完后手里持有一支股票的最大利润（i 从 0 开始）

  1. class Solution {
  2.     public int maxProfit(int[] prices) {
  3.         int n = prices.length;
  4.         int[][] dp = new int[n][2];
  5.         dp[0][0] = 0;
  6.         dp[0][1] = -prices[0];
  7.         for (int i = 1; i < n; ++i) {
  8.             dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
  9.             dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
  10.         }
  11.         return dp[n - 1][0];
  12.     }
  13. }

15【中等】打家劫舍 II（213）

image.png

  1. class Solution {
  2.     public int rob(int[] nums) {
  3.         int length = nums.length;
  4.         if (length == 1) {
  5.             return nums[0];
  6.         } else if (length == 2) {
  7.             return Math.max(nums[0], nums[1]);
  8.         }
  9.         return Math.max(robRange(nums, 0, length - 2), robRange(nums, 1, length - 1));
  10.     }
  12.     public int robRange(int[] nums, int start, int end) {
  13.         int first = nums[start], second = Math.max(nums[start], nums[start + 1]);
  14.         for (int i = start + 2; i <= end; i++) {
  15.             int temp = second;
  16.             second = Math.max(first + nums[i], second);
  17.             first = temp;
  18.         }
  19.         return second;
  20.     }
  21. }