数组

  • 数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。

    1.1 【简单】两数之和（1）

    image.png
    1. /**
    2. * 利用map 
    3. * a + b = target那么b = target - a; 可以用O(n)的空间Set来存储原始数组，
    4. * 然后计算target-a是否在Set中。
    5. */
    6. public int[] twoSum(int[] nums, int target) {
    7.   Map<Integer, Integer> map = new HashMap<>();
    8.   for (int i = 0; i < nums.length; i++) {
    9.       if (map.get(nums[i]) != null) {
    10.           return new int[]{map.get(nums[i]), i};
    11.       }
    12.       map.put(target - nums[i], i);
    13.   }
    14.   return new int[2];
    15. }

    1.2 【中等】三数之和（15）

    image.png
    1. /**
    2. * 排序后枚举即可
    3. */
    4. public List<List<Integer>> threeSum(int[] nums) {
    5.   int n = nums.length;
    6.   Arrays.sort(nums);
    7.   List<List<Integer>> ans = new ArrayList<List<Integer>>();
    8.   // 枚举 a
    9.   for (int i = 0; i < n; ++i) {
    10.       int target = -nums[i];
    11.       if (i > 0 && nums[i] == nums[i - 1]) {
    12.           continue;
    13.       }
    14.       int third = n - 1;
    15.       for (int second = i+1; second < n; ++second) {
    16.           if (second > i+1 && nums[second] == nums[second - 1]) {
    17.               continue;
    18.           }
    19.           while (second < third && nums[second] + nums[third] > target) {
    20.               third--;
    21.           }
    22.           if (second == third) {
    23.               break;
    24.           }
    25.           if (nums[second] + nums[third] == target) {
    26.               List<Integer> list = new ArrayList<>();
    27.               list.add(nums[i]);
    28.               list.add(nums[second]);
    29.               list.add(nums[third]);
    30.               ans.add(list);
    31.           }
    32.       }
    33.   }
    34.   return ans;
    35. }

    1.3 【简单】删除有序数组中的重复项（26）

    image.png
    1. /**
    2. * 双指针前进，第一个指针走完返回第二个指针索引位置即可
    3. */
    4. public int removeDuplicates(int[] nums) {
    5.   if (nums.length == 0) {
    6.       return 0;
    7.   }
    8.   int temp = nums[0];
    9.   int j = 1;
    10.   for (int i = 1; i < nums.length; i++) {
    11.       if (nums[i] != temp) {
    12.           temp = nums[i];
    13.           nums[j] = nums[i];
    14.           j++;
    15.       }
    16.   }
    17.   return j;
    18. }

    1.4 【简单】移动零（283）

    image.png
    1. /**
    2. * 暴力迁移
    3. */
    4. public void moveZeroes(int[] nums) {
    5.   int num = 0;
    6.   for (int i = 0; i < nums.length; i++) {
    7.       while (nums[i] == 0) {
    8.           if (nums.length - i == num) {
    9.               return;
    10.           }
    11.           int temp = nums[i];
    12.           for (int j = i + 1; j < nums.length; j++) {
    13.               nums[j - 1] = nums[j];
    14.           }
    15.           nums[nums.length - 1] = temp;
    16.           num++;
    17.       }
    18.   }
    19. }

    1.5 【简单】加一（66）

    image.png
    1. /**
    2. * 暴力解法
    3. */
    4. public int[] plusOne(int[] digits) {
    5.   int flag = 0;
    6.   for (int i = digits.length - 1; i >= 0; i--) {
    7.       if (flag == 0 && i != digits.length - 1) {
    8.           break;
    9.       }
    10.       if (digits[i] == 9) {
    11.           flag = 1;
    12.           digits[i] = 0;
    13.       } else {
    14.           digits[i] = digits[i] + 1;
    15.           flag = 0;
    16.       }
    17.   }
    18.   if (flag == 1) {
    19.       int[] result = new int[digits.length + 1];
    20.       result[0] = 1;
    21.       for (int i = 0; i < digits.length; i++) {
    22.           result[i + 1] = digits[i];
    23.       }
    24.       return result;
    25.   } else {
    26.       return digits;
    27.   }
    28. }

    1.6 【简单】合并两个有序数组（88）

    image.png
    1. /**
    2. * 暴力解法
    3. */
    4. public void merge(int[] nums1, int m, int[] nums2, int n) {
    5.   if (n == 0) {
    6.       return;
    7.   }
    8.   int totalNum = m + n;
    9.   int j = 0;
    10.   for (int i = 0; i < totalNum && j < n; i++) {
    11.       if (nums1[i] > nums2[j]) {
    12.           // 往后移动
    13.           for (int k = totalNum - 1; k > i; k--) {
    14.               nums1[k] = nums1[k - 1];
    15.           }
    16.           nums1[i] = nums2[j];
    17.           j++;
    18.       }
    19.   }
    20.   if (j < n) {
    21.       for (int i = totalNum - n + j; i < totalNum; i++) {
    22.           nums1[i] = nums2[j];
    23.           j++;
    24.       }
    25.   }
    26. }

    1.7 【中等】轮转数组（189）

    image.png
    1. /**
    2. * 三次置换
    3. */
    4. public void rotate(int[] nums, int k) {
    5.   k %= nums.length;
    6.   reverse(nums, 0, nums.length - 1);
    7.   reverse(nums, 0, k - 1);
    8.   reverse(nums, k, nums.length - 1);
    9. }
    10. public void reverse(int[] nums, int start, int end) {
    11.   while (start < end) {
    12.       int temp = nums[start];
    13.       nums[start] = nums[end];
    14.       nums[end] = temp;
    15.       start ++;
    16.       end--;
    17.   }
    18. }

    1.8 【困难】素数伴侣（HJ28）

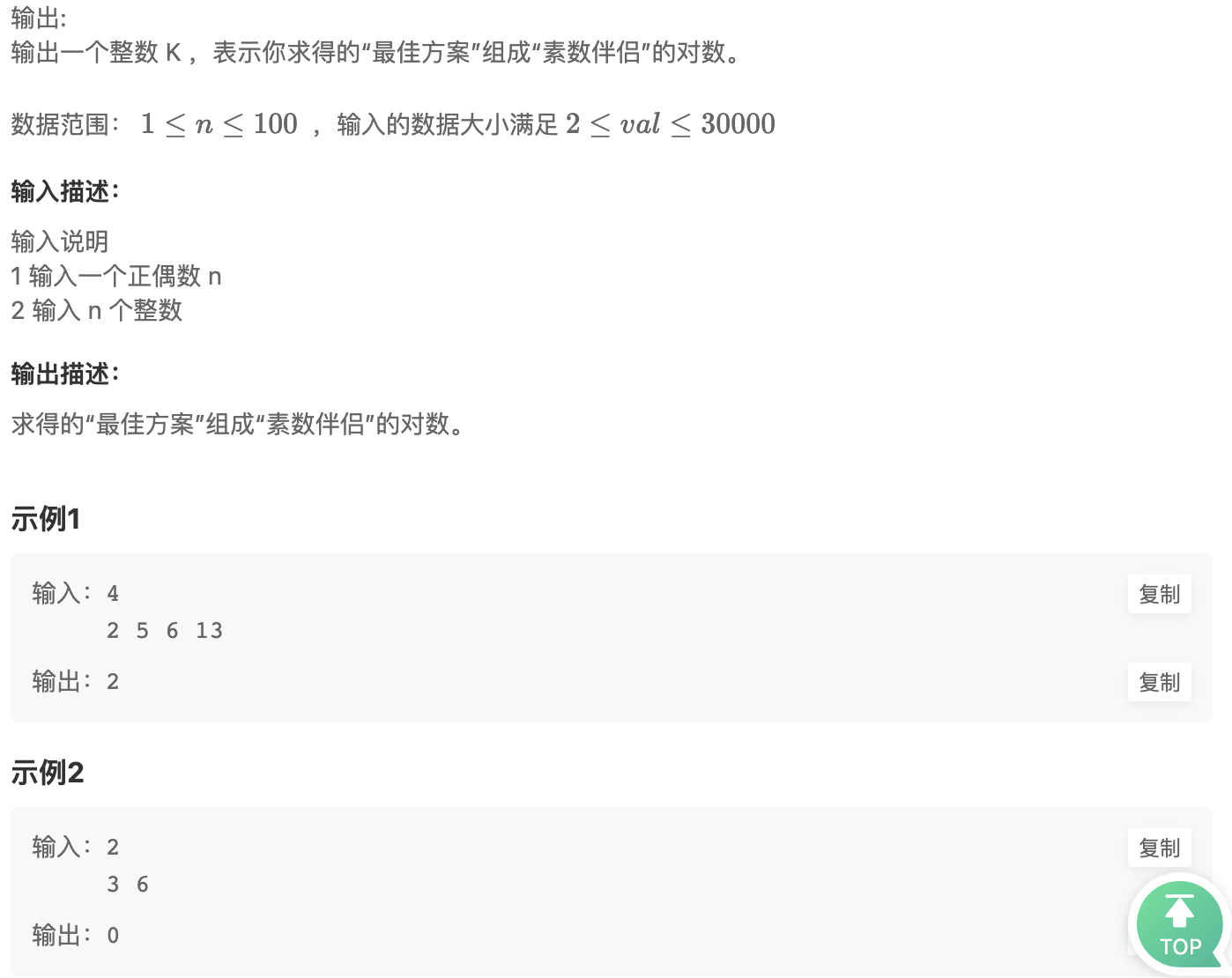
    image.png
    素数必定是偶数加奇数，所以可以分为两个list进行匹配，用到的方法是匈牙利算法，先到先得，能让则让。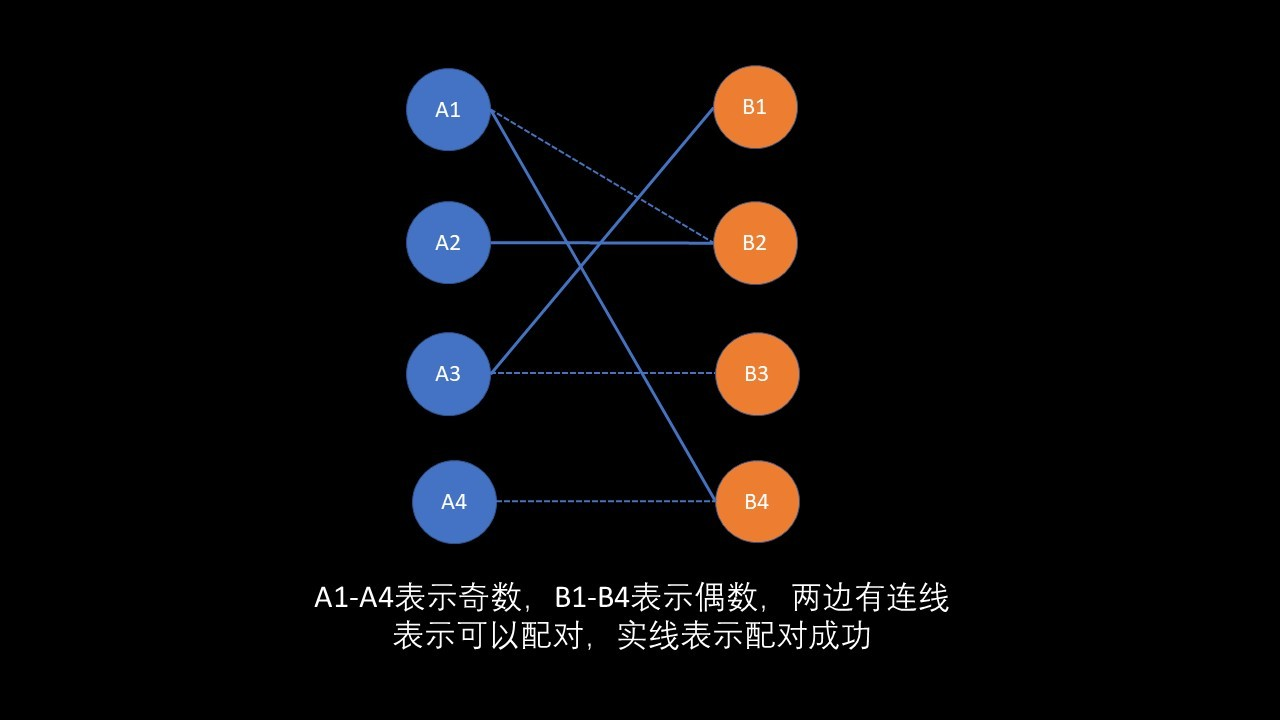
    image.png
    举例说明：如图所示，首先A1和B2配对（先到先得），然后轮到A2，A2也可以和B2配对，这时候B2发现A1还可以和B4配对，所以放弃了A1，选择和A2组成伴侣（能让就让）。接着A3直接和B1配对（先到先得）。最后A4尝试与B4配对，但是这样A1就只能与B2配对，而A2就找不到伴侣了，一层层递归下来，发现不可行，所以A4不能与B4配对。 ```java import java.util.*;

public class Main{

  1. public static void main(String[] args) {
  2.     Scanner sc = new Scanner(System.in);
  3.     while (sc.hasNext()) {
  4.         //输入正偶数
  5.         int n = sc.nextInt();
  6.         //用于记录输入的n个整数
  7.         int[] arr = new int[n];
  8.         //用于存储所有的奇数
  9.         ArrayList<Integer> odds = new ArrayList<>();
  10.         //用于存储所有的偶数
  11.         ArrayList<Integer> evens = new ArrayList<>();
  12.         for (int i = 0; i < n; i++) {
  13.             arr[i] = sc.nextInt();
  14.             //将奇数添加到odds
  15.             if (arr[i] % 2 == 1) {
  16.                 odds.add(arr[i]);
  17.             }
  18.             //将偶数添加到evens
  19.             if (arr[i] % 2 == 0) {
  20.                 evens.add(arr[i]);
  21.             }
  22.         }
  23.         //下标对应已经匹配的偶数的下标，值对应这个偶数的伴侣
  24.         int[] matcheven = new int[evens.size()];
  25.         //记录伴侣的对数
  26.         int count = 0;
  27.         for(int j=0;j<odds.size();j++){
  28.             //用于标记对应的偶数是否查找过
  29.             boolean[] v = new boolean[evens.size()];
  30.             if(find(odds.get(j),matcheven,evens,v)){
  31.                 count++;
  32.             }
  33.         }
  34.         System.out.println(count);
  35.     }
  36. }
  38. private static boolean find(int x, int[] matcheven, ArrayList<Integer> evens, boolean[] v) {
  39.     for(int i=0;i<evens.size();i++){
  40.         //该位置偶数没被访问过，并且能与x组成素数伴侣
  41.         if(isSu(x+evens.get(i))&&!v[i]){
  42.             v[i] = true;
  43.             /* 
  44.              * 如果i位置偶数还没有伴侣，则与x组成伴侣，如果已经有伴侣，并且这个伴侣能重新找到新伴侣，
  45.              * 则把原来伴侣让给别人，自己与x组成伴侣
  46.              */
  47.             if(matcheven[i]==0||find(matcheven[i],matcheven,evens,v)){
  48.                 matcheven[i] = x;
  49.                 return true;
  50.             }
  51.         }
  52.     }
  53.     return false;
  54. }
  56. public static boolean isSu(int num){
  57.     for(int i=2;i<num;i++){
  58.         if(num%i==0){
  59.             return false;
  60.         }
  61.     }
  62.     return true;
  63. }

}

  1. <a name="XMR4y"></a>
  2. #### 1.9 【中等】两个排序数组中的第k小的数，要求时间复杂度为O(logN)（字节真题）
  3. 举例：<br />arr1=[1,2,3,4,5],arr2=[3,4,5],k=1<br />1是所有数中第一小的数，所以返回1<br />arr1=[1,2,3],arr2=[3,4,5,6],k=4<br />3是所有数中第4小的数，所以返回3<br />要求：如果arr1的长度为N，arr2的长度为M,时间复杂度请达到O(log(min{M,N}),额外空间复杂度为O(1)
  4. ```java
  5. public int getUpMedian(int[] arr1, int start1, int end1, int[] arr2, int s
  6.     int mid1 = 0, mid2 = 0;
  7.     //用于判断过程中数组的长度的奇偶
  8.     int offset = 0;
  9.     while (start1 < end1) {
  10.         mid1 = (start1 + end1) / 2;
  11.         mid2 = (start2 + end2) / 2;
  12.         offset = ((end1 - start1 + 1) & 1) ^ 1;
  13.         //元素个数为奇数，offset为0，元素个数为偶数，offset为1
  14.         if (arr1[mid1] > arr2[mid2]) {
  15.             end1 = mid1;
  16.             start2 = mid2 + offset;
  17.         } else if (arr1[mid1] < arr2[mid2]) {
  18.             end2 = mid2;
  19.             start1 = mid1 + offset;
  20.         } else {
  21.             return arr1[mid1];
  22.         }
  23.     }
  24.     return Math.min(arr1[start1], arr2[start2]);
  25. }
  27. public int findKthNum(int[] arr1, int[] arr2, int kth) {
  28.     if (arr1 == null || arr2 == null) {
  29.         throw new RuntimeException("Your arr is invalind");
  30.     }
  31.     if (kth < 1 || kth > arr1.length + arr2.length) {
  32.         throw new RuntimeException("k is invalid");
  33.     }
  34.     int[] longs = arr1.length >= arr2.length ? arr1 : arr2;
  35.     int[] shorts = arr1.length < arr2.length ? arr1 : arr2;
  36.     int l = longs.length;
  37.     int s = shorts.length;
  38.     if (kth <= s) {
  39.         //在shortArr中选前面k个数,在longArr中也选前面k个数
  40.         // 则两段数组的上中位数就是第k小数
  41.         return getUpMedian(shorts, 0, kth - 1, longs, 0, kth - 1);
  42.     }
  43.     if (kth > l) {
  44.         // shorts[kth - l - 1]大于longs的所有数字，那么shorts[kth - l - 1]即为答案
  45.         if (shorts[kth - l - 1] >= longs[l - 1]) {
  46.             return shorts[kth - l - 1];
  47.         }
  48.         // 同理
  49.         if (longs[kth - s - 1] >= shorts[s - 1]) {
  50.             return longs[kth - s - 1];
  51.         }
  52.         // 取后面的中位数
  53.         return getUpMedian(shorts, kth - 1, s - 1, longs, kth - s, l - 1);
  54.     }
  55.     // len(s)<k<len(l)，如果longs[kth - s - 1]比所有shorts都大，那么即为答案
  56.     if (longs[kth - s - 1] >= shorts[s - 1]) {
  57.         return longs[kth - s - 1];
  58.     }
  59.     // 取中位数
  60.     return getUpMedian(shorts, 0, s - l, longs, kth - s, kth - 1);
  61. }

参考：https://www.cnblogs.com/pathjh/p/9096652.html

2.链表

2.1 【简单】反转链表（206）

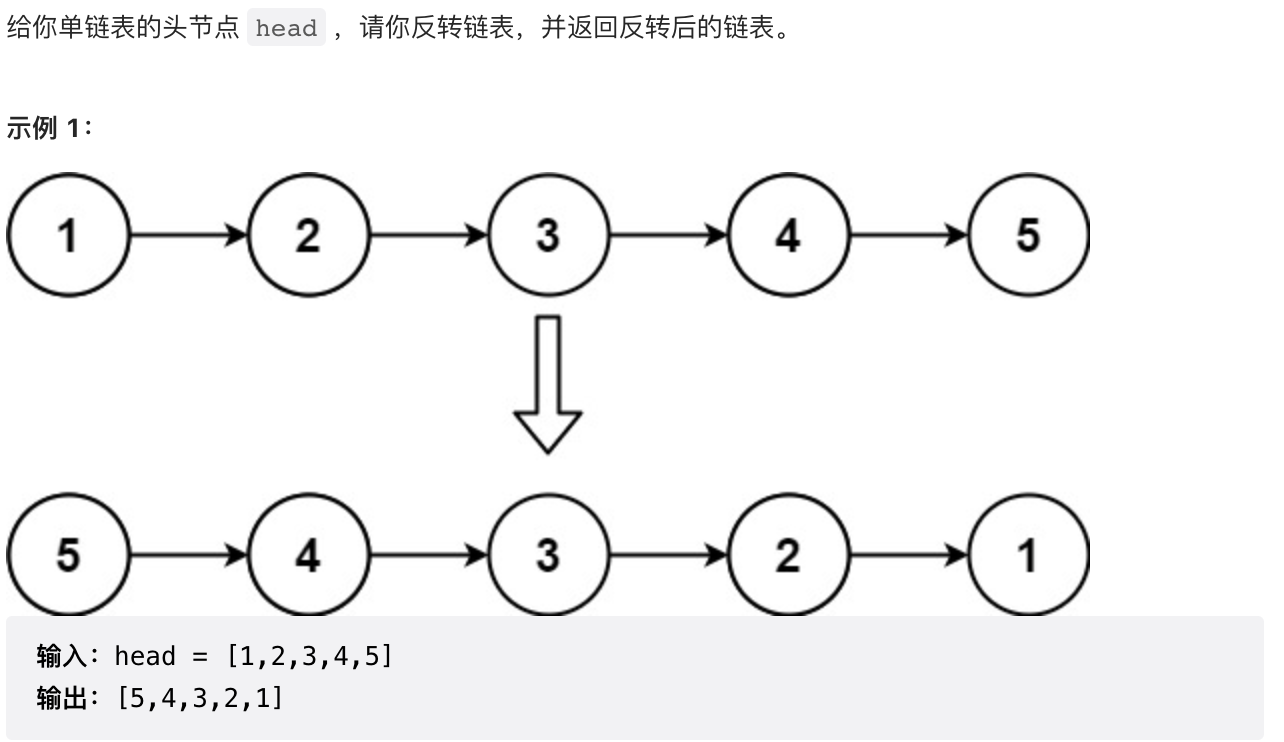
image.png

  1. /**
  2.  * 需要记忆
  3.  */
  4. public ListNode reverseList(ListNode head) {
  5.     if (null == head || null == head.next) {
  6.         return head;
  7.     }
  8.     ListNode curr = head;
  9.     ListNode prev = null;
  10.     while (curr != null) {
  11.         ListNode next = curr.next;
  12.         curr.next = prev;
  13.         prev = curr;
  14.         curr = next;
  15.     }
  16.     return prev;
  17. }

2.2 【简单、中等】链表中有环（141, 142）

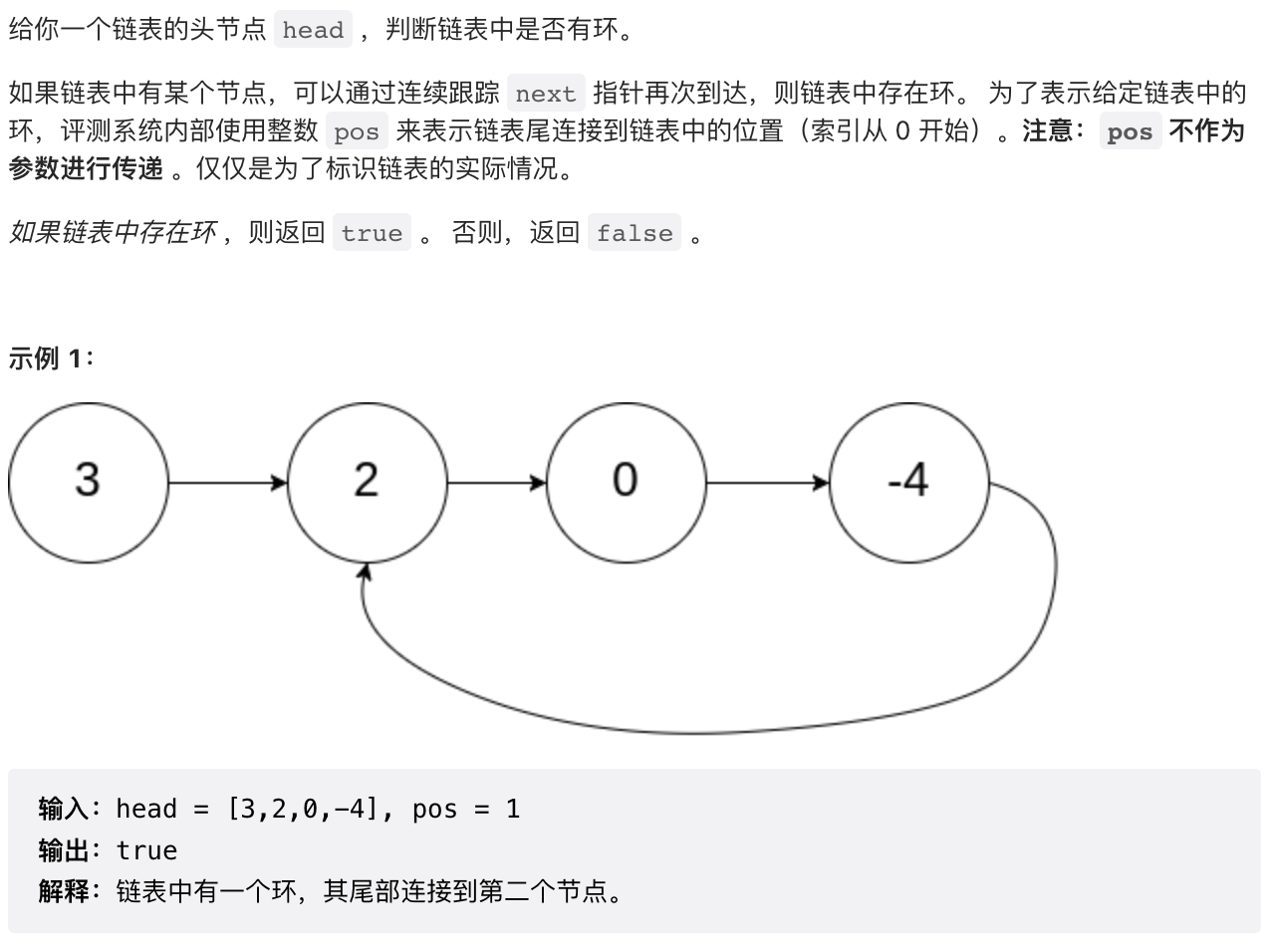
image.png

  1. /**
  2.  * 快慢指针
  3.  */
  4. public boolean hasCycle(ListNode head) {
  5.     if (head == null || head.next == null) {
  6.         return false;
  7.     }
  8.     ListNode slow = head;
  9.     ListNode fast = head.next;
  10.     while (slow != fast) {
  11.         if (fast == null || fast.next == null) {
  12.             return false;
  13.         }
  14.         slow = slow.next;
  15.         fast = fast.next.next;
  16.     }
  17.     return true;
  18. }

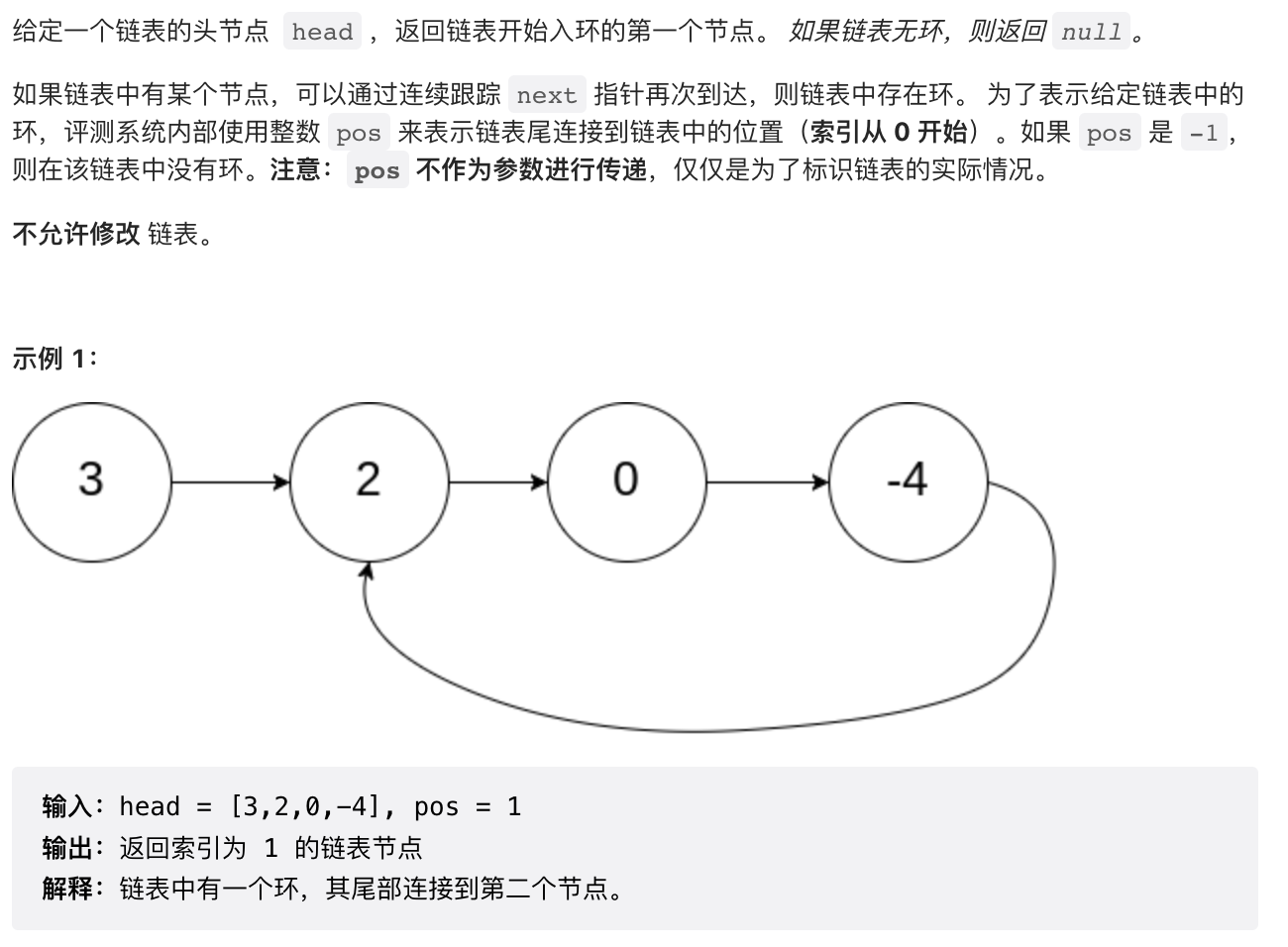
image.png

  1. /**
  2.  * 快慢指针，需要推导一个等式 a=c+(n-1)(b+c)a=c+(n−1)(b+c) 
  3.  */
  4. public ListNode detectCycle(ListNode head) {
  5.     if (head == null) {
  6.         return null;
  7.     }
  8.     ListNode slow = head, fast = head;
  9.     while (fast != null) {
  10.         slow = slow.next;
  11.         if (fast.next != null) {
  12.             fast = fast.next.next;
  13.         } else {
  14.             return null;
  15.         }
  16.         if (fast == slow) {
  17.             ListNode ptr = head;
  18.             while (ptr != slow) {
  19.                 ptr = ptr.next;
  20.                 slow = slow.next;
  21.             }
  22.             return ptr;
  23.         }
  24.     }
  25.     return null;
  26. }

2.3 【简单】合并两个有序链表（21）

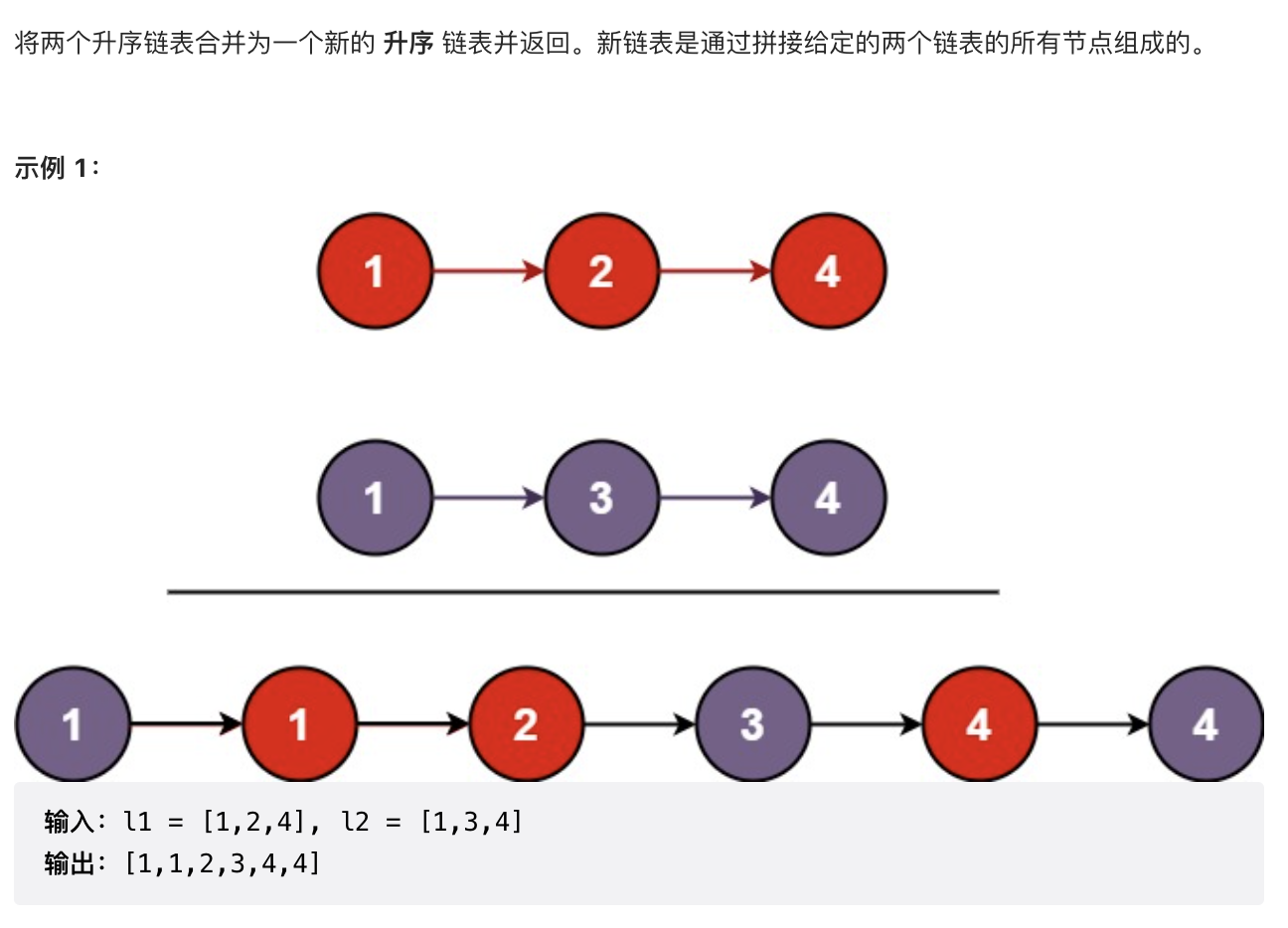
image.png

  1. /**
  2.  * list1与list2往下走即可
  3.  */
  4. public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
  5.     ListNode result = new ListNode();
  6.     ListNode prev = result;
  7.     while (list1 != null && list2 != null) {
  8.         if (list1.val < list2.val) {
  9.             prev.next = list1;
  10.             list1 = list1.next;
  11.         } else {
  12.             prev.next = list2;
  13.             list2 = list2.next;
  14.         }
  15.         prev = prev.next;
  16.     }
  17.     prev.next = list1 == null ? list2 : list1;
  18.     return result.next;
  19. }

2.4 【中等】删除链表倒数第 n 个结点（19）

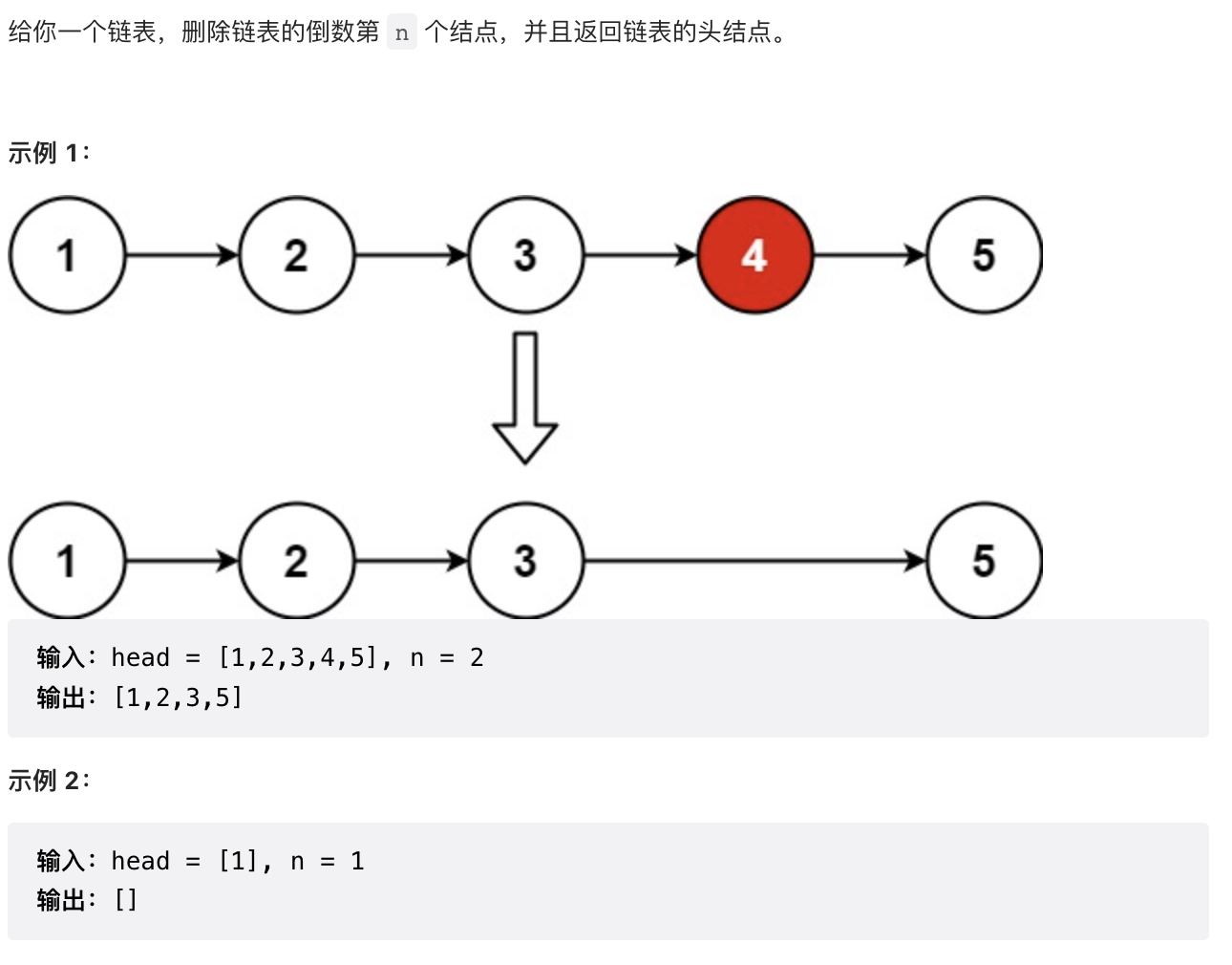
image.png

  1. /**
  2.  * 涉及到删除结点的需要一个dummy
  3.  */
  4. public ListNode removeNthFromEnd(ListNode head, int n) {
  5.     ListNode dummy = new ListNode(0, head);
  6.     ListNode front = head;
  7.     // 抽象头节点
  8.     ListNode temp = dummy;
  9.     for (int i = 0; i < n; ++i) {
  10.         front = front.next;
  11.     }
  12.     while (front != null) {
  13.         front = front.next;
  14.         temp = temp.next;
  15.     }
  16.     temp.next = temp.next.next;
  17.     return dummy.next;
  18. }

2.5 【简单】求链表的中间结点（876）

image.png

  1. /**
  2.  * 用数组即可简单实现
  3.  */
  4. public ListNode middleNode(ListNode head) {
  5.     ListNode[] nodeArr = new ListNode[100];
  6.     int count = 0;
  7.     while (head != null) {
  8.         nodeArr[count] = head;
  9.         ++count;
  10.         head = head.next;
  11.     }
  12.     return nodeArr[count / 2];
  13. }

2.6 【中等】两两交换链表中的节点（24）

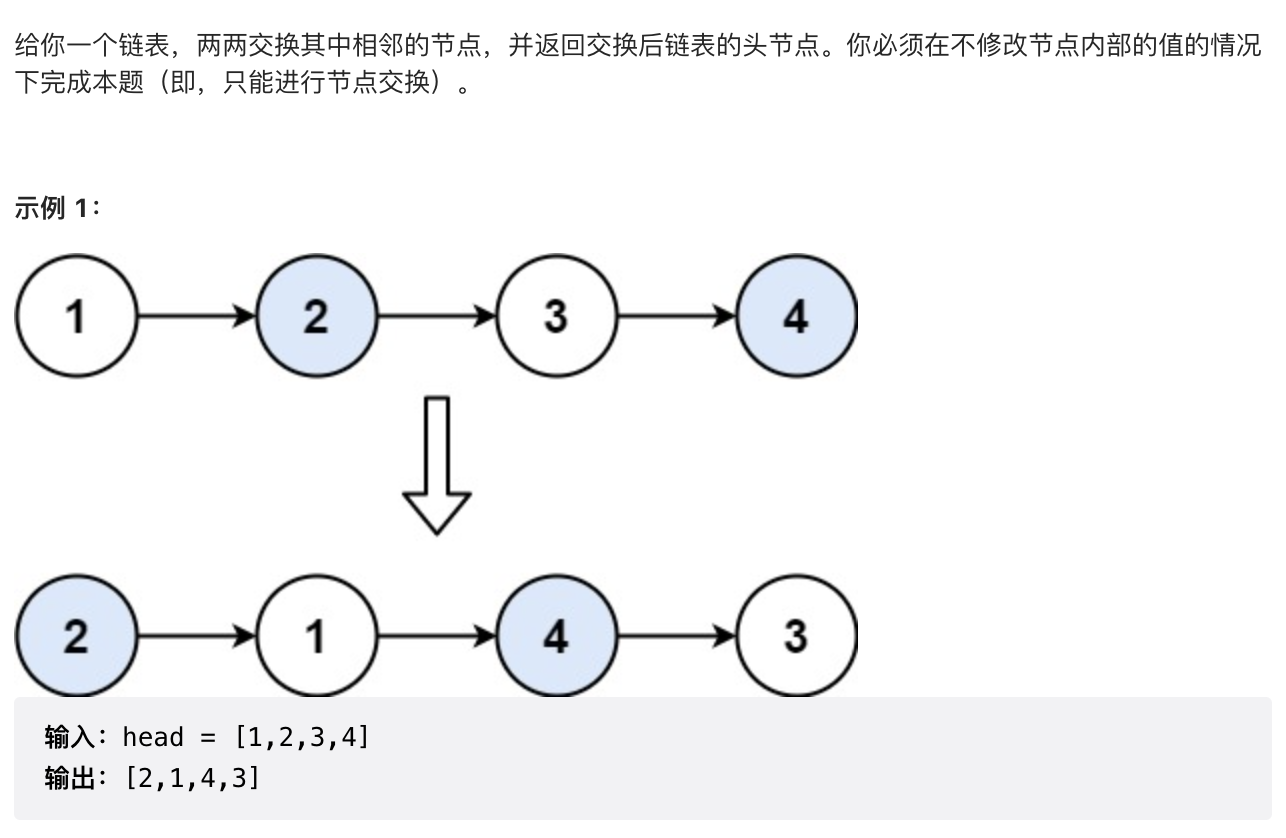
image.png

  1. /**
  2.  * 需要dummy以及后两个节点
  3.  */
  4. public ListNode swapPairs(ListNode head) {
  5.     // 持有head
  6.     ListNode dummyHead = new ListNode();
  7.     dummyHead.next = head;
  8.     ListNode first = dummyHead;
  9.     while (first.next != null && first.next.next != null) {
  10.         ListNode second = first.next;
  11.         ListNode third = second.next;
  12.         // 交换
  13.         first.next = third;
  14.         second.next = third.next;
  15.         third.next = second;
  16.         // 移动到下一轮
  17.         first = second;
  18.     }
  19.     return dummyHead.next;
  20. }

2.7 【中等】LRU 缓存（146）

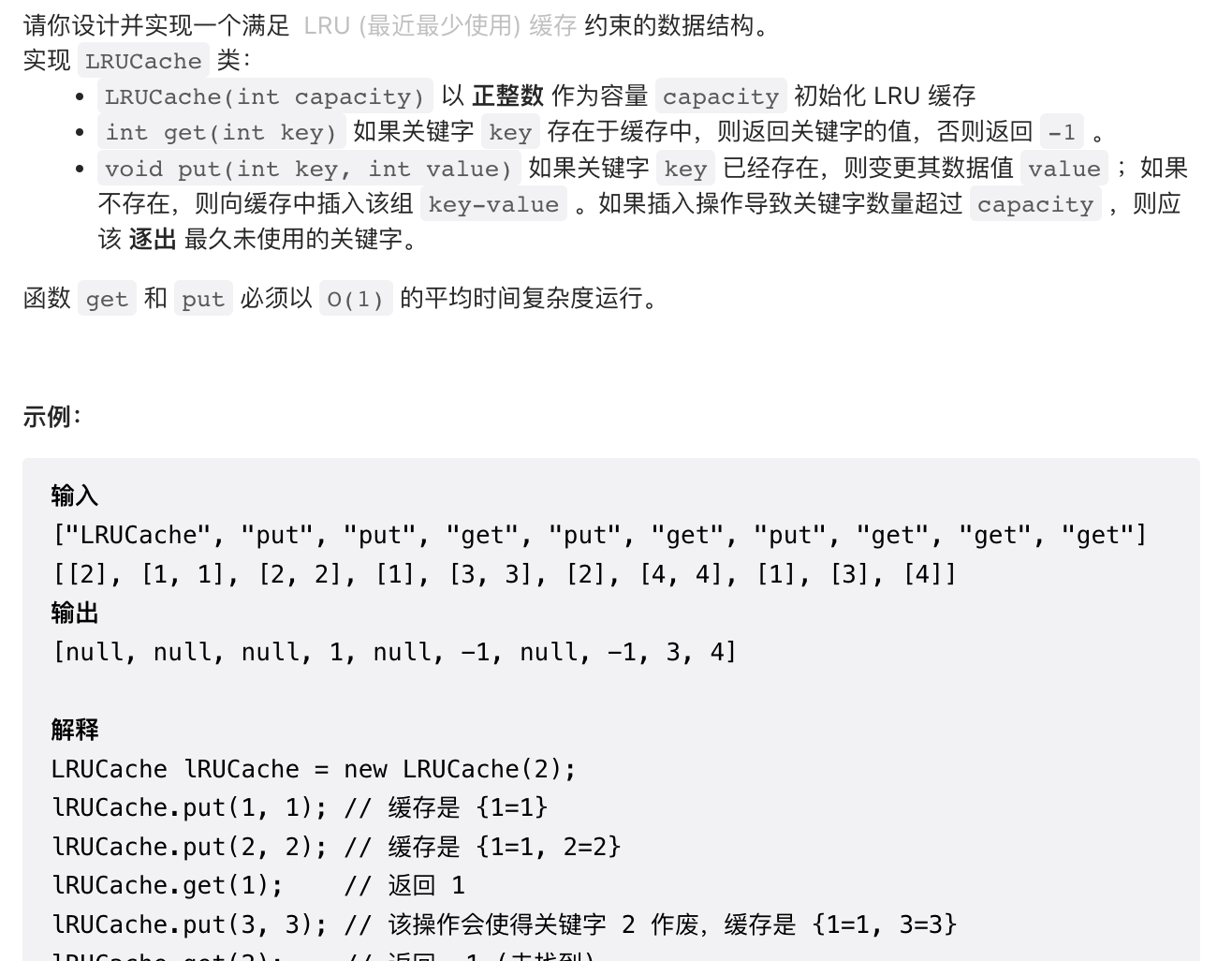
image.png

  1. /**
  2.  * 重写LinkedHashMap即可
  3.  */
  4. class LRUCache extends LinkedHashMap<Integer, Integer> {
  6.     private int capacity;
  8.     public LRUCache(int capacity) {
  9.         super(capacity, 0.75F, true);
  10.         this.capacity = capacity;
  11.     }
  13.     public int get(int key) {
  14.         return super.getOrDefault(key, -1);
  15.     }
  17.     public void put(int key, int value) {
  18.         super.put(key, value);
  19.     }
  21.     @Override
  22.     protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
  23.         return size() > capacity;
  24.     }
  25. }

2.8 【中等】剑指 Offer II 077. 链表排序

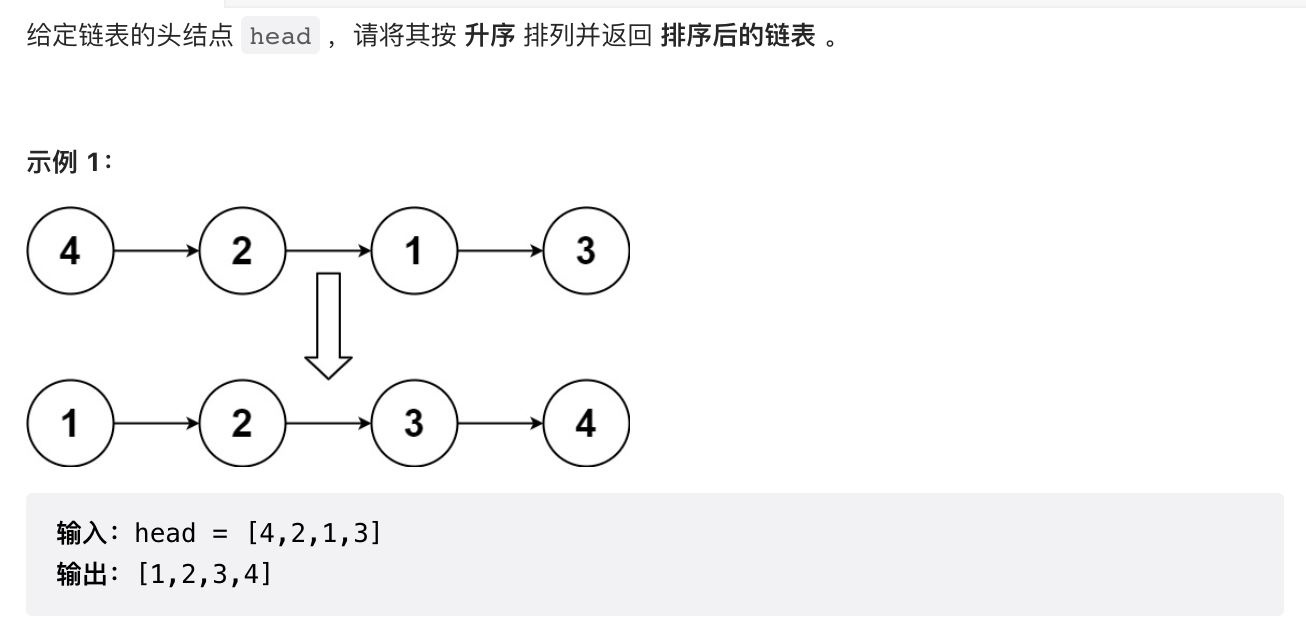
image.png

  1. public class SortList {
  2.     public ListNode sortList(ListNode head) {
  3.         return sortList(head, null);
  4.     }
  6.     public ListNode sortList(ListNode head, ListNode tail) {
  7.         if (head == null) {
  8.             return null;
  9.         }
  10.         if (head.next == tail) {
  11.             head.next = null;
  12.             return head;
  13.         }
  14.         // 寻找中点
  15.         ListNode slow = head, fast = head;
  16.         while (fast != tail) {
  17.             slow = slow.next;
  18.             fast = fast.next;
  19.             if (fast != tail) {
  20.                 fast = fast.next;
  21.             }
  22.         }
  23.         ListNode mid = slow;
  24.         ListNode list1 = sortList(head, mid);
  25.         ListNode list2 = sortList(mid, tail);
  26.         // 合并链表
  27.         return merge(list1, list2);
  28.     }
  30.     public ListNode merge(ListNode head1, ListNode head2) {
  31.         ListNode dummyHead = new ListNode(0);
  32.         ListNode temp = dummyHead, temp1 = head1, temp2 = head2;
  33.         while (temp1 != null && temp2 != null) {
  34.             if (temp1.val <= temp2.val) {
  35.                 temp.next = temp1;
  36.                 temp1 = temp1.next;
  37.             } else {
  38.                 temp.next = temp2;
  39.                 temp2 = temp2.next;
  40.             }
  41.             temp = temp.next;
  42.         }
  43.         if (temp1 != null) {
  44.             temp.next = temp1;
  45.         } else if (temp2 != null) {
  46.             temp.next = temp2;
  47.         }
  48.         return dummyHead.next;
  49.     }
  50. }

2.9 【困难】K 个一组翻转链表（25）

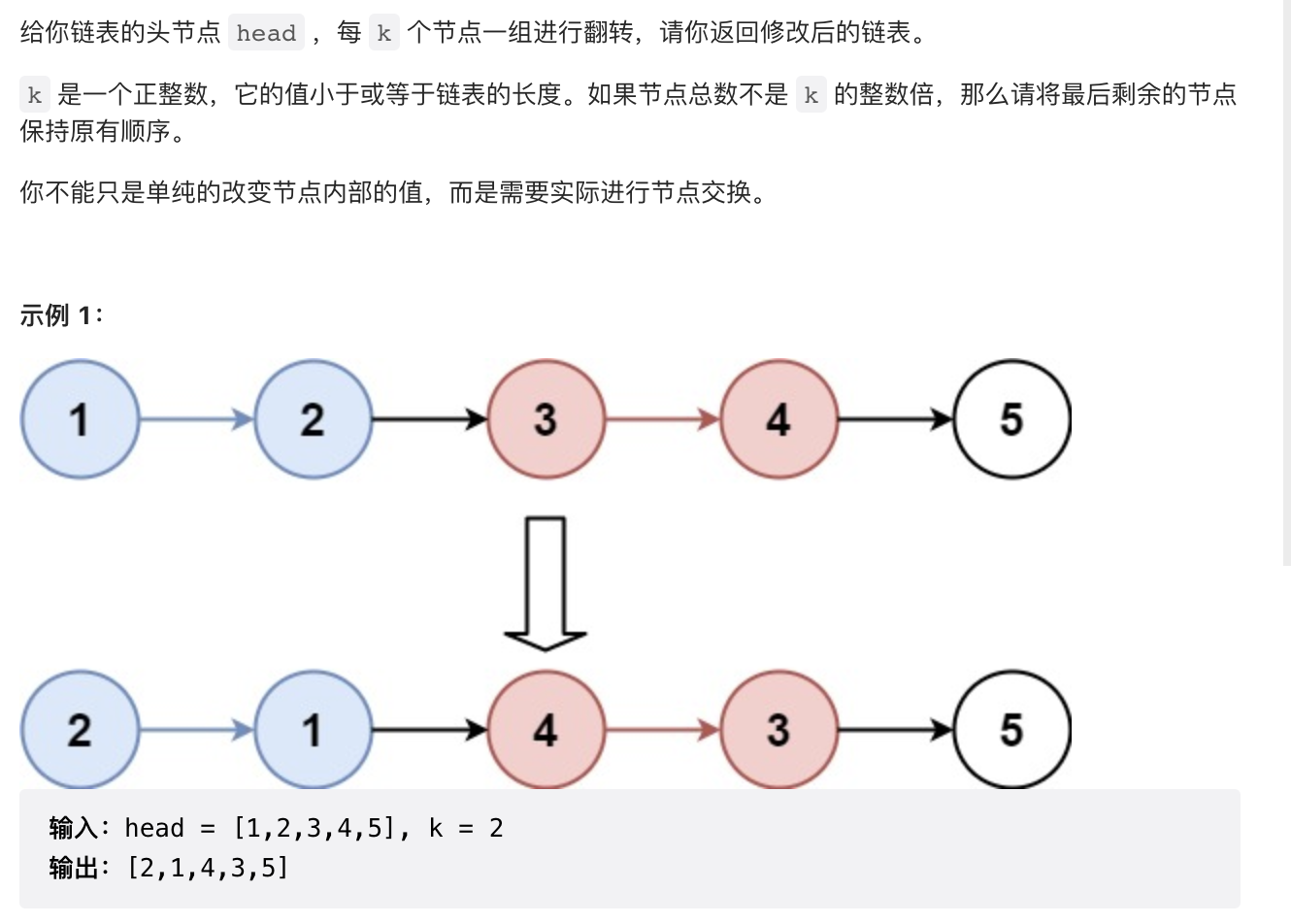
image.png

  1. class Solution {
  2.     public ListNode reverseKGroup(ListNode head, int k) {
  3.         ListNode hair = new ListNode(0);
  4.         hair.next = head;
  5.         ListNode pre = hair;
  7.         while (head != null) {
  8.             ListNode tail = pre;
  9.             // 查看剩余部分长度是否大于等于 k
  10.             for (int i = 0; i < k; ++i) {
  11.                 tail = tail.next;
  12.                 if (tail == null) {
  13.                     return hair.next;
  14.                 }
  15.             }
  16.             ListNode nex = tail.next;
  17.             ListNode[] reverse = myReverse(head, tail);
  18.             head = reverse[0];
  19.             tail = reverse[1];
  20.             // 把子链表重新接回原链表
  21.             pre.next = head;
  22.             tail.next = nex;
  23.             pre = tail;
  24.             head = tail.next;
  25.         }
  27.         return hair.next;
  28.     }
  30.     public ListNode[] myReverse(ListNode head, ListNode tail) {
  31.         // 反转
  32.         ListNode prev = tail.next;
  33.         ListNode p = head;
  34.         while (prev != tail) {
  35.             ListNode nex = p.next;
  36.             p.next = prev;
  37.             prev = p;
  38.             p = nex;
  39.         }
  40.         return new ListNode[]{tail, head};
  41.     }
  42. }