聚类业务 聚类算法

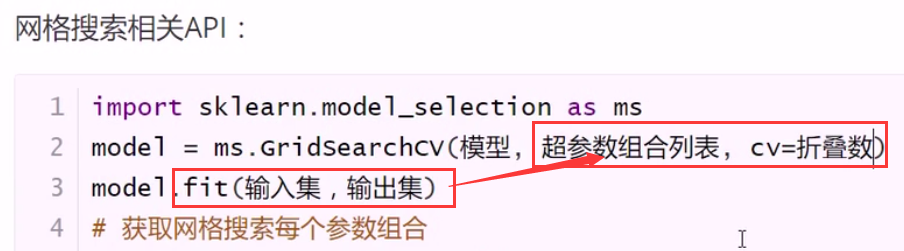
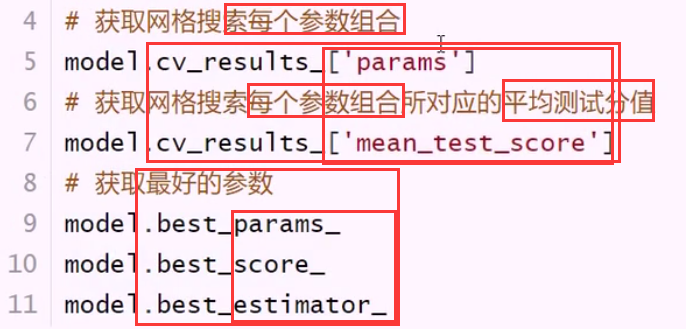
无法验证

消除 随机k个聚类中心的 随机性，要迭代

告诉了要分七个类，但一开始的选择中心是随机

重新聚类时，有些点分类被改变

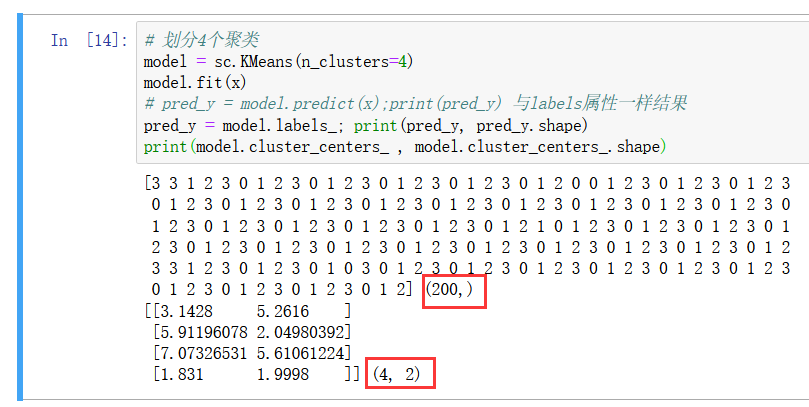
两个模型副产品属性，都是数组

查看样本分布： 大概分为四队

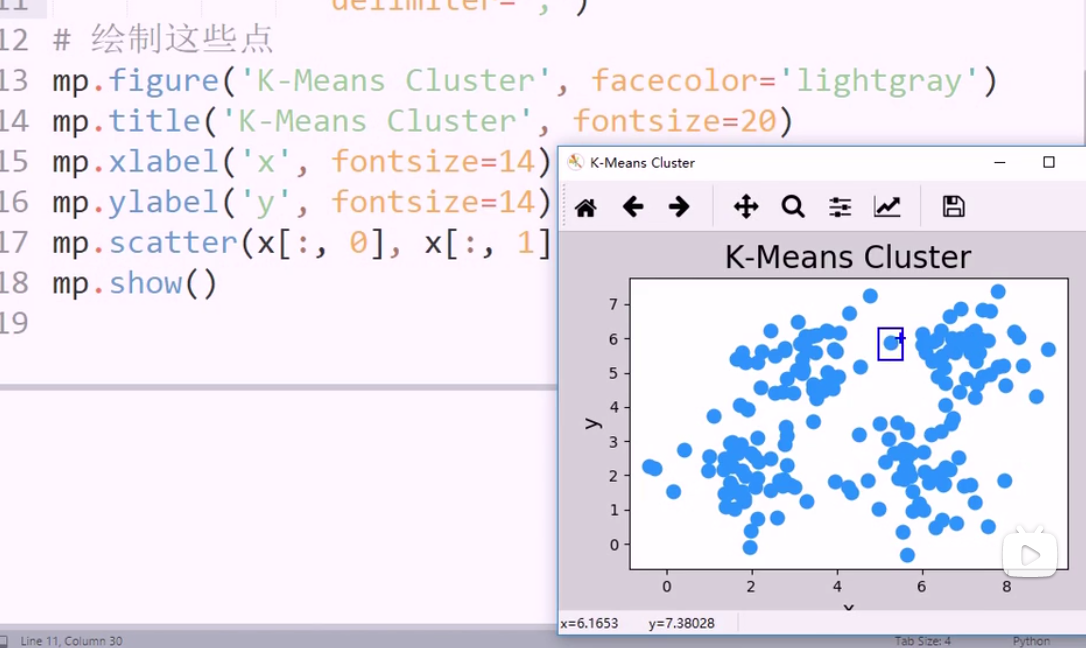
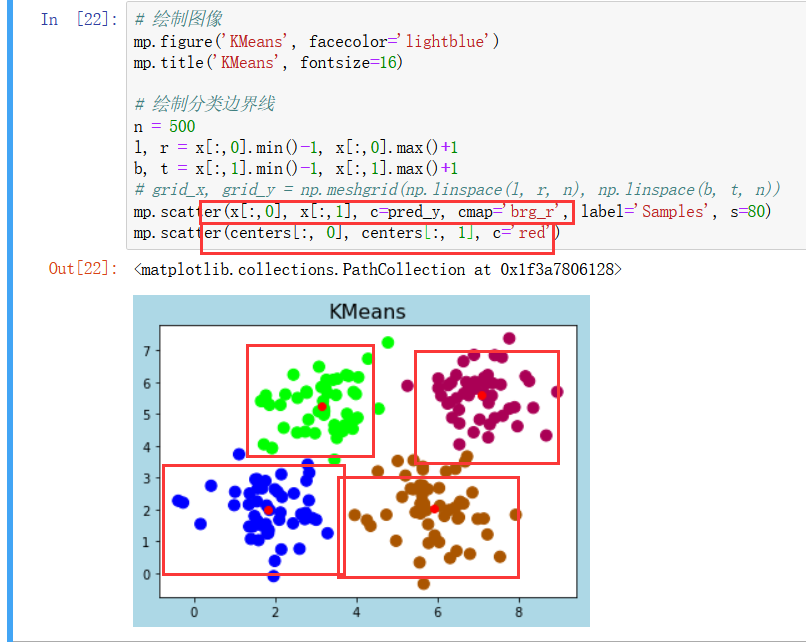
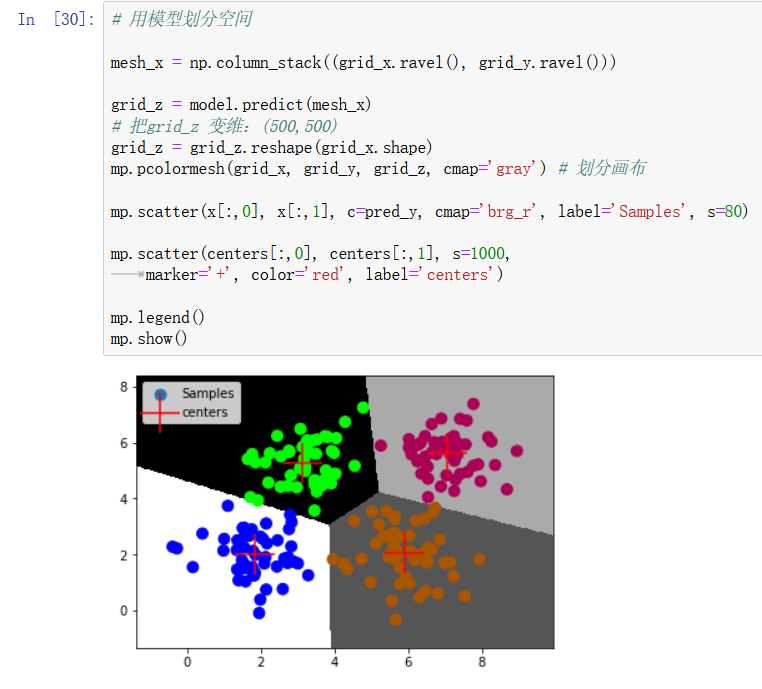
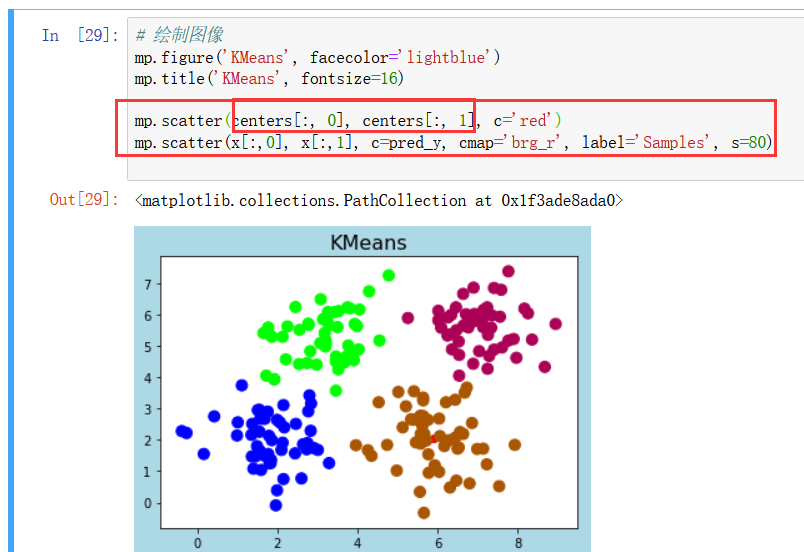注意可能相互覆盖 绘图顺序

图像变换： 更改灰度值，原有范围0-255，改为4种数字，16.。100.。160.。210

大小离谁近改为谁 该亮的还亮，该暗的还暗，就像打了马赛克

相当于一维数组 250000个元素，做kmeans

简单的图形更好做轮廓识别

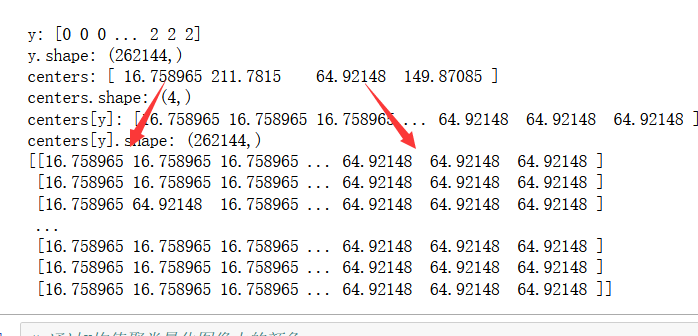
最强掩码： 索引掩码，将4值数组centers 用作填充，y 25000 数组中就是centers的下标，作为掩码，最终被修改的是y

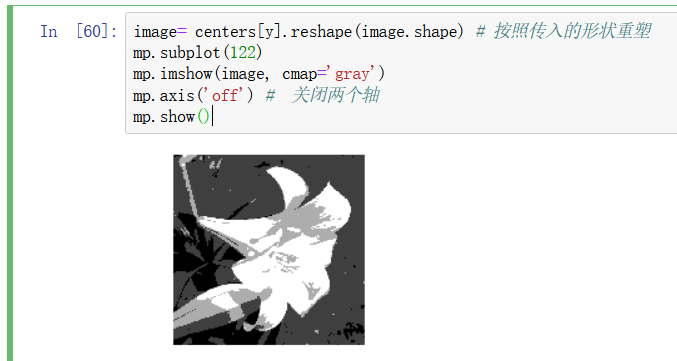
聚类10个

均值漂移算法

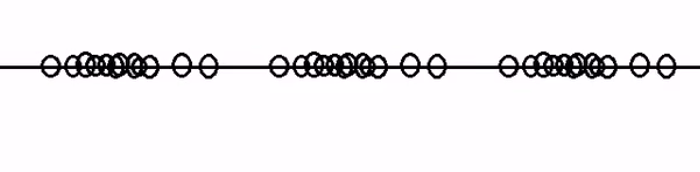
用高斯分布，看图说话：

样本空间如下

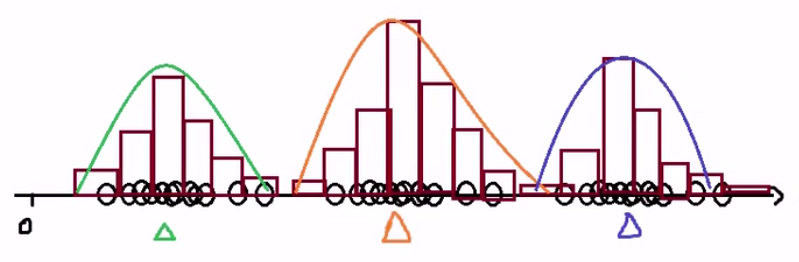
绘制统计直方图： 看每个区间的样本数

用高斯函数拟合这些直方图： 一边移动一边拟合

有最佳匹配位置，就是发现了一个聚类中心

用新的高斯函数再平移拟合，反复找到所有聚类中心

对所有样本进行欧拉距离，归类到找到的中心上

柱子的宽度十分重要， 当柱子太窄，会产生过多中心

x 样本空间

TRUE 一个带宽移动一下 FALSE 移动慢更精准，但很慢 用true就好

业务需求： 不想定聚类数量，此时考虑使用漂移

不知道应该聚合成为几个类 改带宽

案例： 仍是图片，改为模型kmeans 为漂移

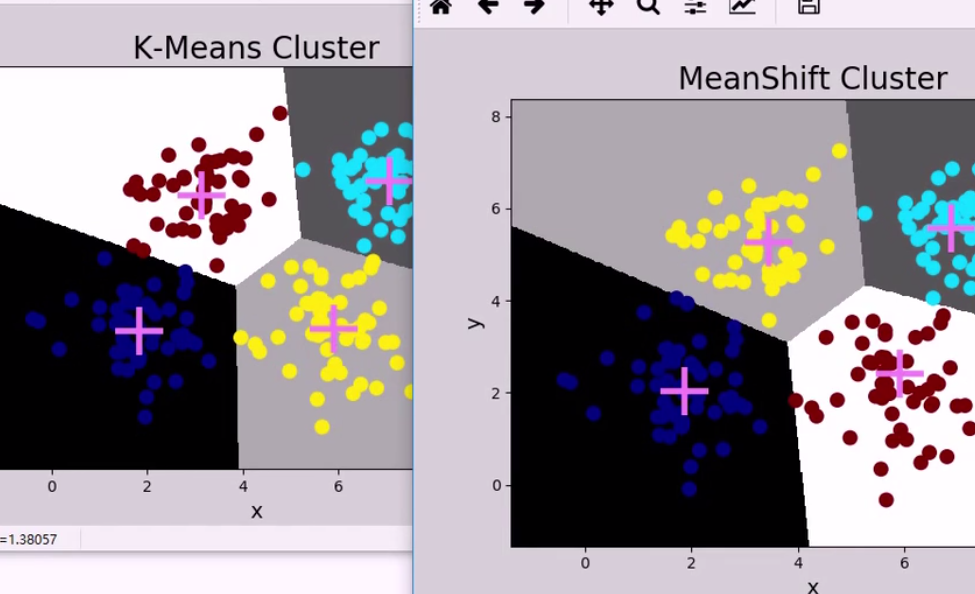分布良好，则预测效果很好

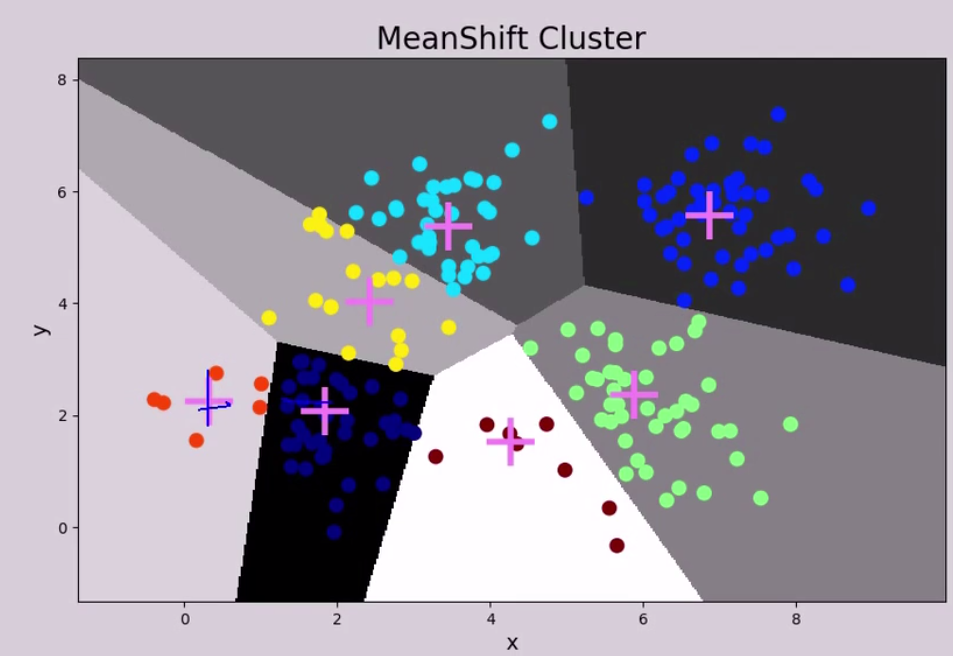量化带宽改为 0.08时，分类中心明显变多

0.02 的带宽

kmeans 必须确定聚类组数

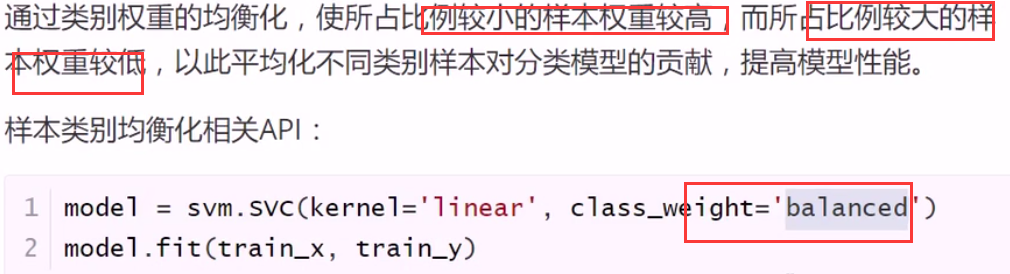
再谈样本均衡化

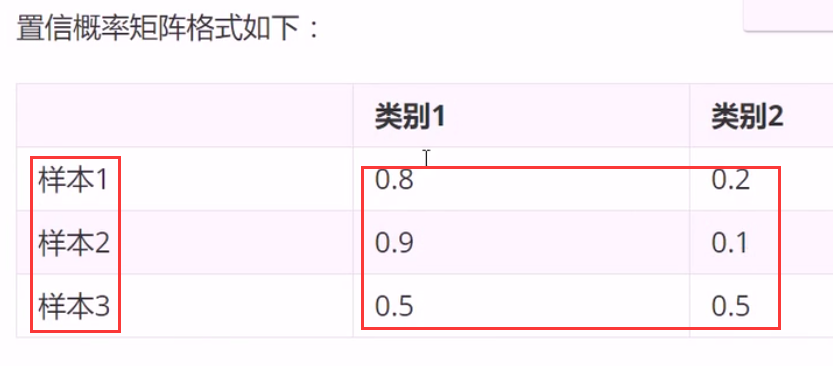
错到什么程度？ 错了但不严重，才0.6