参考博客：https://zhuanlan.zhihu.com/p/31852747
参考视频：
https://www.bilibili.com/video/BV1T7411T7wa/?spm_id_from=333.788.recommend_more_video.-1
https://www.bilibili.com/video/BV14E411H7Uw/?spm_id_from=333.788.recommend_more_video.0
代码：https://github.com/WZMIAOMIAO/deep-learning-for-image-processing
我的理解：

ResNet

1)为什么读这个? Why am I reading this?

2)作者写这篇文章的目的是什么? What are the authors trying to achieve in writing this?

3)作者所述与我的研究的相关之处是什么? What are the authors claiming that is relevant to
my work?

4)作者的这些阐述的有多可信，为什么呢? How convincing are these claims and why?

5)这篇文章对我有什么用? In conclusion, what use can I make of it?

作者写这篇文章的目的是什么?

ResNet是解决了深度CNN模型难训练的问题

深度网络的退化问题

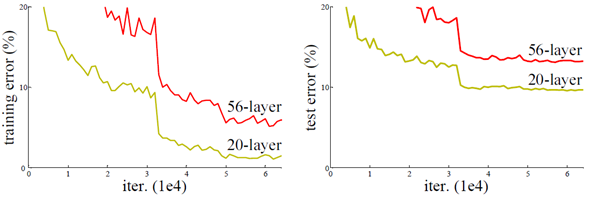
从经验来看，网络的深度对模型的性能至关重要，当增加网络层数后，网络可以进行更加复杂的特征模式的提取，所以当模型更深时理论上可以取得更好的结果，从图2中也可以看出网络越深而效果越好的一个实践证据。但是更深的网络其性能一定会更好吗？实验发现深度网络出现了退化问题（Degradation problem）：网络深度增加时，网络准确度出现饱和，甚至出现下降。这个现象可以在图3中直观看出来：56层的网络比20层网络效果还要差。这不会是过拟合问题，因为56层网络的训练误差同样高。我们知道深层网络存在着梯度消失或者爆炸的问题，这使得深度学习模型很难训练。但是现在已经存在一些技术手段如BatchNorm来缓解这个问题。因此，出现深度网络的退化问题是非常令人诧异的。

2141 - Resnet - 图1

残差学习

深度网络的退化问题至少说明深度网络不容易训练。但是我们考虑这样一个事实：现在你有一个浅层网络，你想通过向上堆积新层来建立深层网络，一个极端情况是这些增加的层什么也不学习，仅仅复制浅层网络的特征，即这样新层是恒等映射（Identity mapping）。在这种情况下，深层网络应该至少和浅层网络性能一样，也不应该出现退化现象。好吧，你不得不承认肯定是目前的训练方法有问题，才使得深层网络很难去找到一个好的参数。

这个有趣的假设让何博士灵感爆发，他提出了残差学习来解决退化问题。对于一个堆积层结构（几层堆积而成）当输入为 2141 - Resnet - 图2 时其学习到的特征记为 2141 - Resnet - 图3 ，现在我们希望其可以学习到残差 2141 - Resnet - 图4 ，这样其实原始的学习特征是 2141 - Resnet - 图5 。之所以这样是因为残差学习相比原始特征直接学习更容易。当残差为0时，此时堆积层仅仅做了恒等映射，至少网络性能不会下降，实际上残差不会为0，这也会使得堆积层在输入特征基础上学习到新的特征，从而拥有更好的性能。残差学习的结构如图4所示。这有点类似与电路中的“短路”，所以是一种短路连接（shortcut connection）。

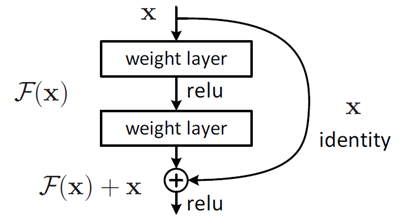
2141 - Resnet - 图6

为什么残差学习相对更容易，从直观上看残差学习需要学习的内容少，因为残差一般会比较小，学习难度小点。不过我们可以从数学的角度来分析这个问题，首先残差单元可以表示为：

2141 - Resnet - 图7

其中 2141 - Resnet - 图8 和 2141 - Resnet - 图9 分别表示的是第 2141 - Resnet - 图10 个残差单元的输入和输出，注意每个残差单元一般包含多层结构。 2141 - Resnet - 图11 是残差函数，表示学习到的残差，而 2141 - Resnet - 图12 表示恒等映射， 2141 - Resnet - 图13 是ReLU激活函数。基于上式，我们求得从浅层 2141 - Resnet - 图14 到深层 2141 - Resnet - 图15 的学习特征为：

2141 - Resnet - 图16

利用链式规则，可以求得反向过程的梯度：

2141 - Resnet - 图17

式子的第一个因子 2141 - Resnet - 图18 表示的损失函数到达 2141 - Resnet - 图19 的梯度，小括号中的1表明短路机制可以无损地传播梯度，而另外一项残差梯度则需要经过带有weights的层，梯度不是直接传递过来的。残差梯度不会那么巧全为-1，而且就算其比较小，有1的存在也不会导致梯度消失。所以残差学习会更容易。要注意上面的推导并不是严格的证明。

作者：小小将
链接：https://zhuanlan.zhihu.com/p/31852747
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

目标检测网络相关