21001 - 为什么分类问题的损失函数采用交叉熵而不是均方误差MSE？

假设给定输入为x，label为y，其中y的取值为0或者1，是一个分类问题。我们要训练一个最简单的Logistic Regression来学习一个函数f(x)使得它能较好的拟合label，如下图所示。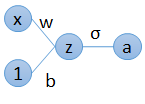

其中 ， 。
也即，我们要学的函数 。目标为使a(x)与label y越逼近越好。用哪种Loss来衡量这个逼近呢？我们可以回忆下交叉熵Loss和均方差Loss定义是什么：

1. 最小均方误差，MSE（Mean Squared Error）Loss
   
2. 交叉熵误差CEE（Cross Entropy Error）Loss
   

我们想衡量模型输出a和label y的逼近程度，其实这两个Loss都可以。但是为什么Logistic Regression采用的是交叉熵作为损失函数呢？看下这两个Loss function对w的导数，也就是SGD梯度下降时，w的梯度。

1. 最小均方差
   
2. 交叉熵
   
   由于 ，则：

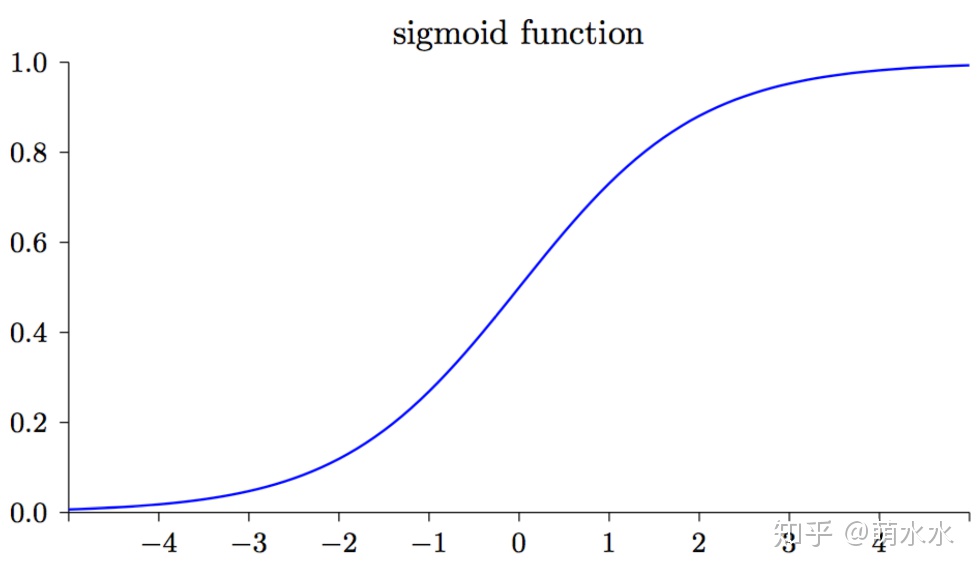
sigmoid函数 如下图所示，可知的导数sigmoid 在输出接近 0 和 1 的时候是非常小的，故导致在使用最小均方差Loss时，模型参数w会学习的非常慢。而使用交叉熵Loss则没有这个问题。为了更快的学习速度，分类问题一般采用交叉熵损失函数。

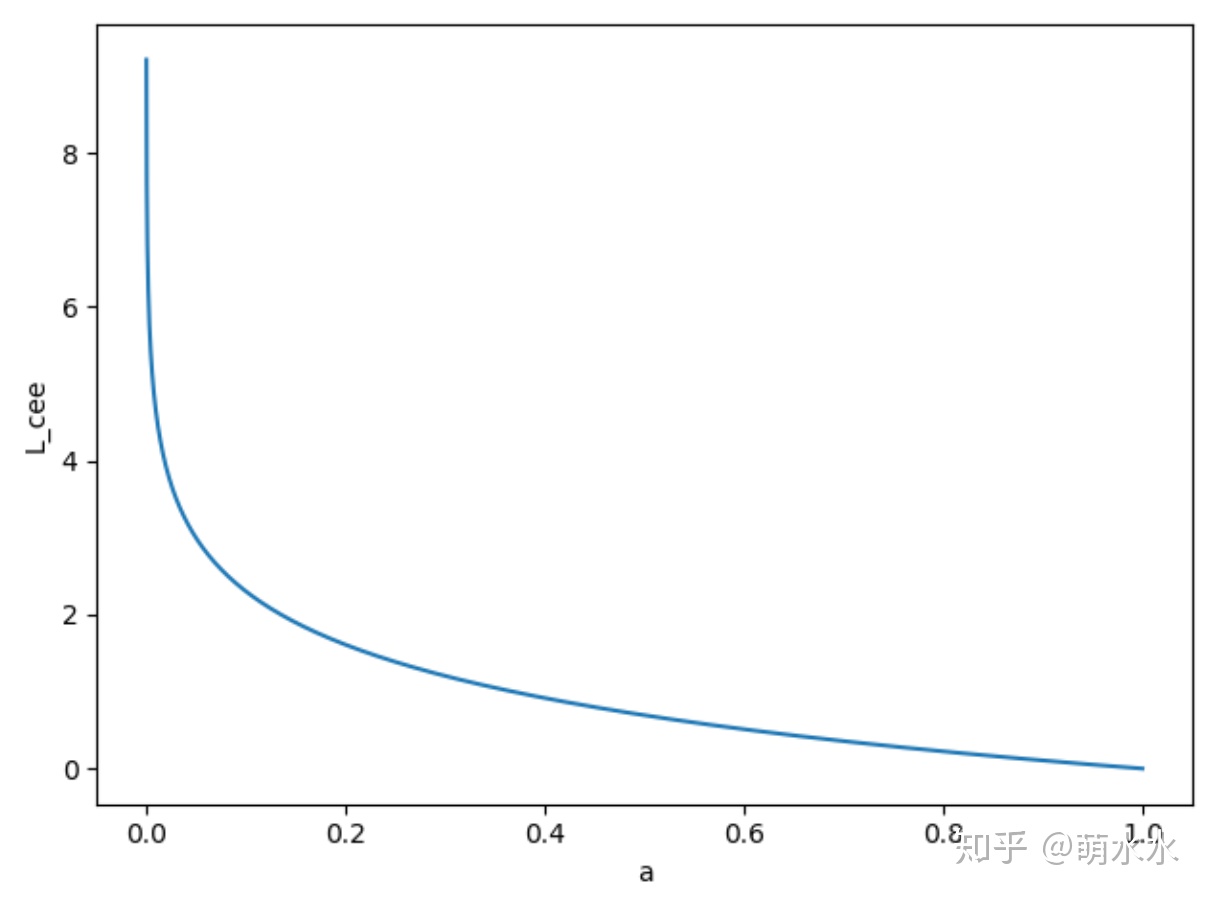
当label = 1，也即 ，交叉熵损失函数
如图所示，可知交叉熵损失函数的值域为