本文总结了batch size和learning rate对模型训练的影响。
1 Batch size对模型训练的影响
使用batch之后，每次更新模型的参数时会拿出一个batch的数据进行更新，所有的数据更新一轮后代表一个epoch。每个epoch之后都会对数据进行shuffle的操作以改变不同batch的数据。
假设训练数据一共有 
个，黄色的叉号代表最优的权重 
。
如下图1左图所示为 
时 (即Full Batch)的情况，在这种情况下必须把 
个训练数据都看完才进行一次参数的更新。所以在1个epoch中只更新1次参数。
右图所示为 
时的情况。在这种情况下看1个训练数据就进行一次参数的更新。所以在1个epoch中要更新20次参数。
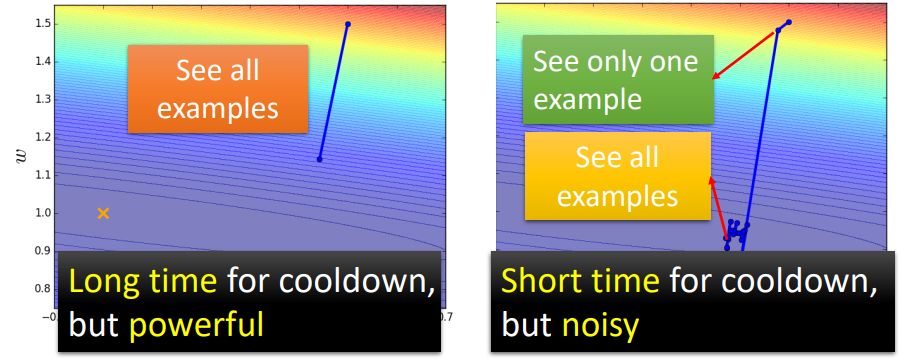图1：batch size为Full或1时的情况
我们发现当batch size = 1时每次的参数更新是比较Noisy的，所以今天参数更新的方向是曲曲折折的。左边这种方式的 “蓄力” 时间比较长，你需要把所有的数据都看过一遍，才能够update一次参数。右边这种方式的 “蓄力” 时间比较短，每次看过一笔数据，就能够update一次参数，属于乱枪打鸟型。
问：左边跟右边哪种比较好呢？
答：看起来各自有各自的优缺点。你可能会说：左边技能冷却时间比较长，右边技能冷却时间比较短。但是，你其实没有考虑到 平行计算 的问题。实际情况是：比较大的batch size，你算loss，进而算gradient的时间 不一定 比小的batch size要长。如下图2所示是在V100上测试得到的MNIST数据集上bs=1到1000的时间，几乎是一样的。直觉上1000笔资料计算gradient的时间是1笔资料的1000倍，但是实际上呢，因为GPU平行计算的缘故，这个时间是十分接近的。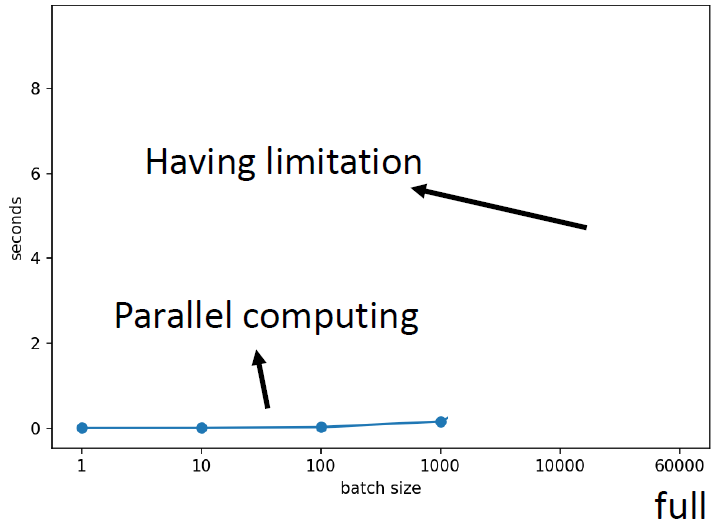
图2：比较大的batch size，你算loss，进而算gradient的时间 不一定 比小的batch size要长
所以实际上，因为平行计算的缘故，当你的batch size小的时候，跑完1个epoch所花的时间其实是比大的batch size多的，如图3所示。因为batch size大的时候可能需要60次的update，但是batch size小的时候可能就需要60000次。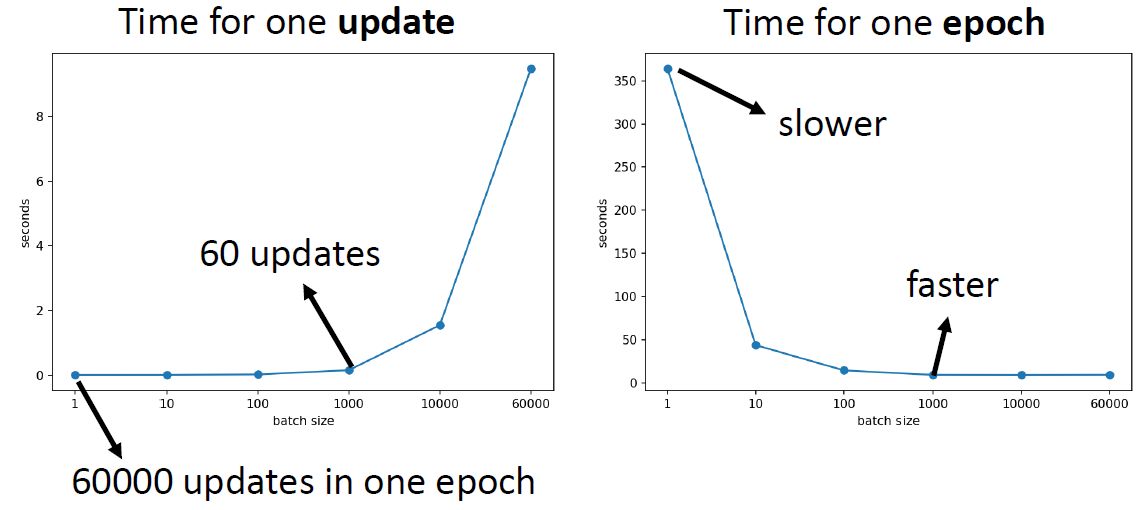
图3：因为平行计算的缘故，当你的batch size小的时候，跑完1个epoch所花的时间其实是比大的batch size多的
所以结论就是：大的batch size其实是比较有效率的。
所以目前已经得到的结论是：大的batch size蓄力时间长，更新比较稳定，且更有效率。
好像全是优势。
但是神奇的地方是：小的batch size的Noisy的更新，反而可能帮助Training。
如下图4所示为在MNIST和CIFAR-10数据集上Acc随着不同batch size的变化情况。我们可以看到，随着batch size越来越大，其实validation结果越差。这是因为overfitting了吗？不是，因为此时的training的结果也是越来越差的。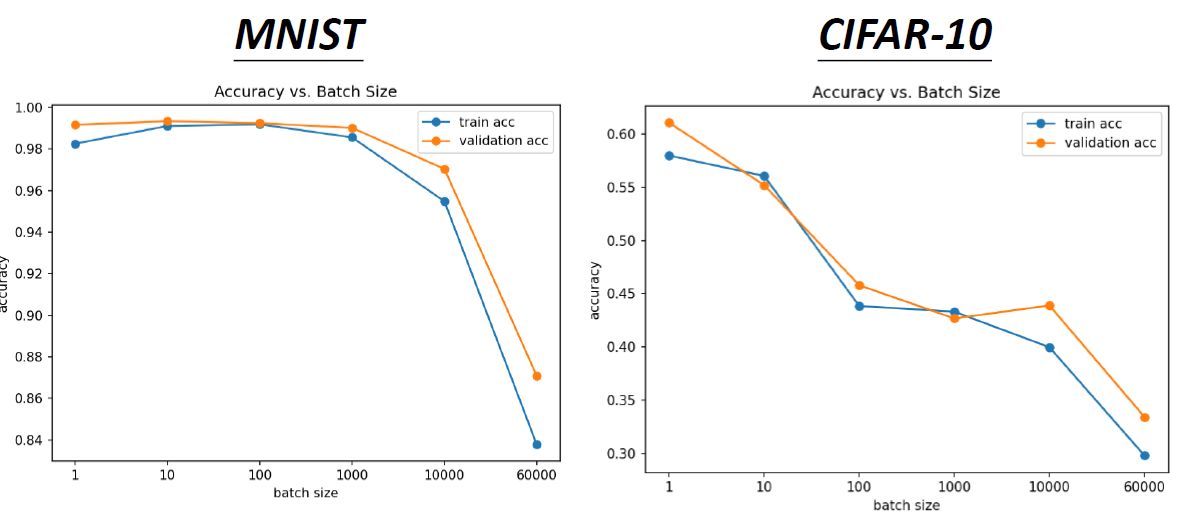
图4：MNIST和CIFAR-10数据集上Acc随着不同batch size的变化情况
这个现象的一种解释如下图5所示。当选择Full Batch的时候，当更新到鞍点时会停止更新。而当选择Small Batch的时候，比如选择了第1笔data，相当于是用绿色的loss更新；而当选择了第2笔data，相当于是用蓝色的loss更新。那么当一个loss陷入鞍点时，其他的data的更新会使得模型走出鞍点。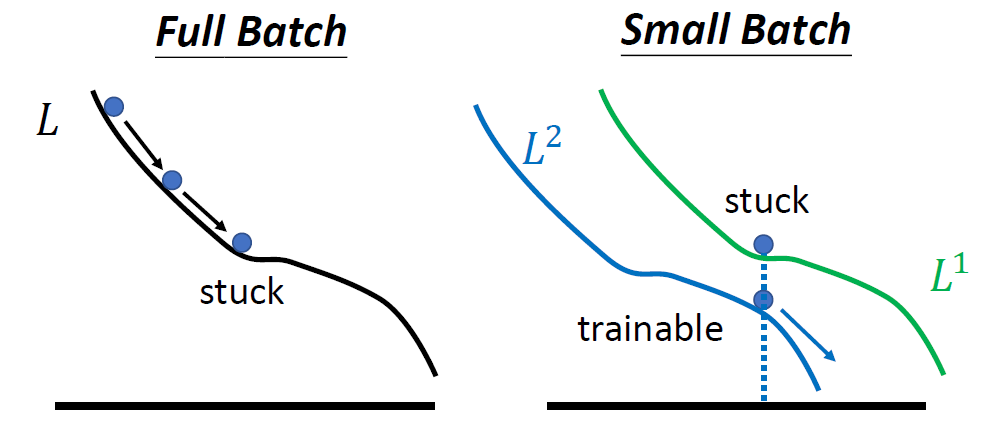
图5：上述现象的解释
另一个有趣的现象是：小的batch其实对testing acc是有帮助的。
为什么有这个现象呢？
如下图6所示，假设黑色的实线为Training loss的曲线，它存在不同类型的minima。其中处于一个相对平坦的minima我们叫做Flat minima，而处于一个相对峡谷的minima我们叫做Sharp minima。而我们认为Flat minima是要好于Sharp minima的，因为Testing Loss的曲线很可能就在Training Loss的附近。而如果今天你的参数优化到了Sharp minima，那么很可能就会得到一个非常大的Testing loss，进而影响性能，所以Flat minima是要好于Sharp minima的。
而小的batch其实是更有利于收敛到Flat minima，因为在计算gradient的时候会有很多的Noisy，这些Noisy的gradient使得曲线很有可能跳出Sharp minima，而优化到Flat minima的位置。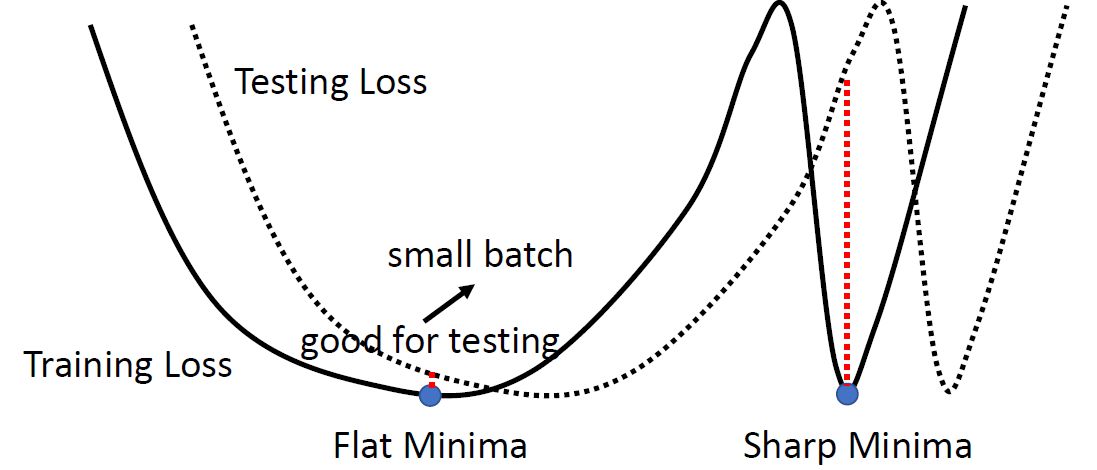
图6：小的batch其实对testing acc是有帮助的
下表是比较了一下不同batch size的特点：
| 小batch size | 大 batch size | |
|---|---|---|
| 每次update的速度(不含平行计算) | 快 | 慢 |
| 每次update的速度(含平行计算) | 一样 | 几乎一样 |
| 训练一个epoch的时间 | 慢 | 快 |
| Gradient | Noisy | Stable |
| Optimization | 更好 | 不好 |
| 泛化能力 | 更好 | 不好 |
2 Learning rate对模型训练的影响
如下图7所示是一个convex的error surface，两个坐标轴代表不同的权值，黄色的叉号代表global optimization的权值参数。如果今天取 
，其结果如左图所示，loss出现振荡；如果今天取 
，其结果如右图所示，不再振荡了，但训练无法走到终点，因为这么小的learning rate根本无法使训练前进。
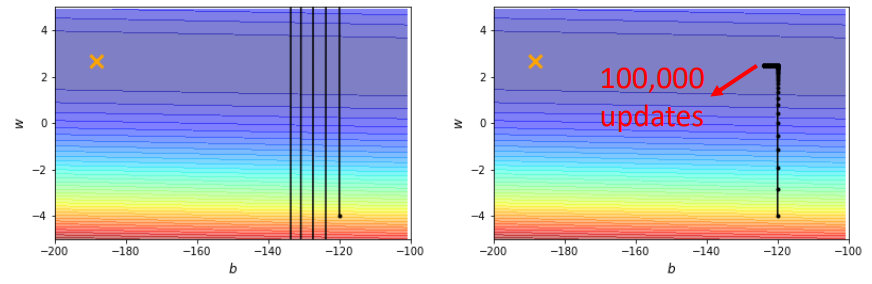图7：不同Learning rate的影响
那怎么把gradient descent做得更好呢？
所以我们要把learning rate特殊化。那么应该怎么特殊化呢？如图8所示，应该在梯度比较逗的纵轴设置小的learning rate，而在梯度比较平坦的横轴设置大的learning rate。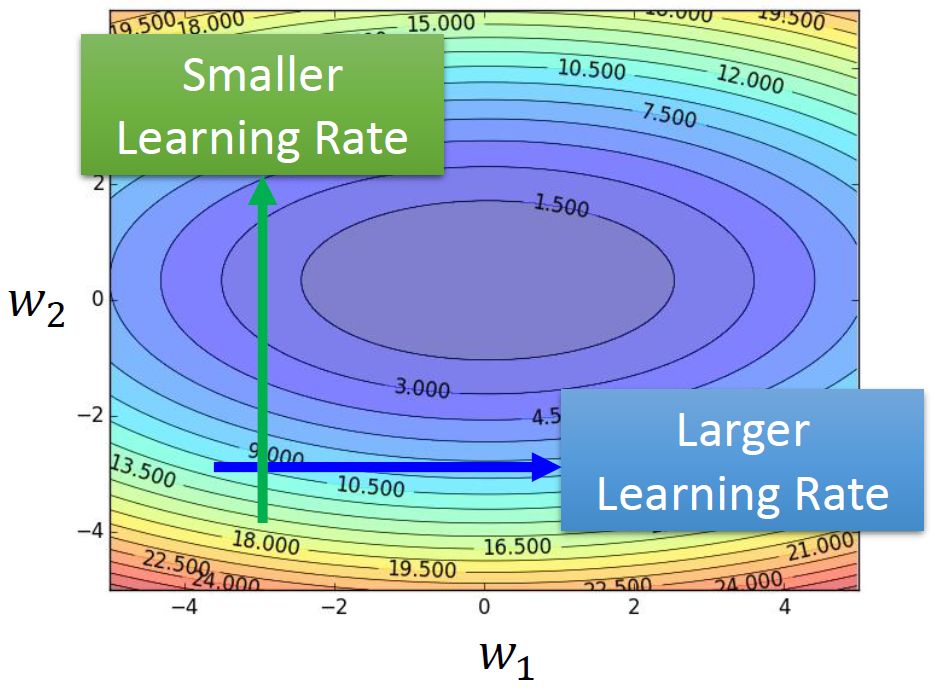
图8：梯度比较逗的纵轴设置小的learning rate，而在梯度比较平坦的横轴设置大的learning rate
假设有参数 
，第 
次更新时的表达式为：
现在要把学习率 
特殊化，就是让 
与 
有关。
这样一来学习率就即与参数有关，又与更新的次数 
有关了。
现在的问题是： 
应该如何来取呢？
有一种Root Mean Square的办法是这样的：
就是每次的 
都是前面梯度的Root Mean Square，这种方法叫做Adagrad，它可以实现坡度比较大时的学习率较小以及坡度比较小时候的学习率较大。
但是这种方法还有一个问题，如图9所示。对于图9所示的error surface来说，同样是横轴，绿色箭头部分的梯度比较大，所以要使用更大的learning rate；而红色箭头部分的梯度比较小，所以要使用更小的learning rate。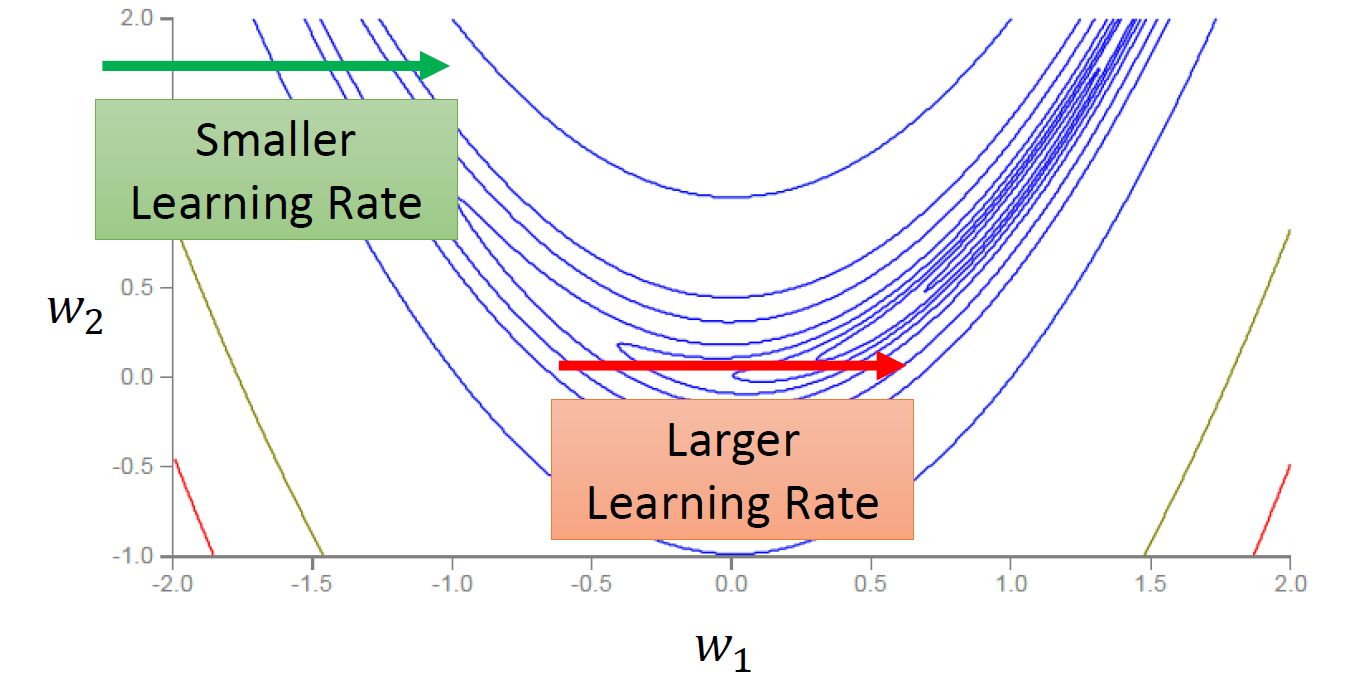
图9：RMSprop解决陡峭程度不同的问题
RMSprop方法就是为了解决这个问题：
RMSprop
就是每次的 
都既考虑本次的梯度，也考虑之前的梯度。这个权重由 
来决定， 
越小，代表当前这个step的梯度 
越重要； 
越大，代表之前所有step的梯度 
越重要。如下图10所示，当陡峭程度不同时，在陡的地方会增加sigma，减少学习率。在缓的地方会减小sigma，增大学习率。
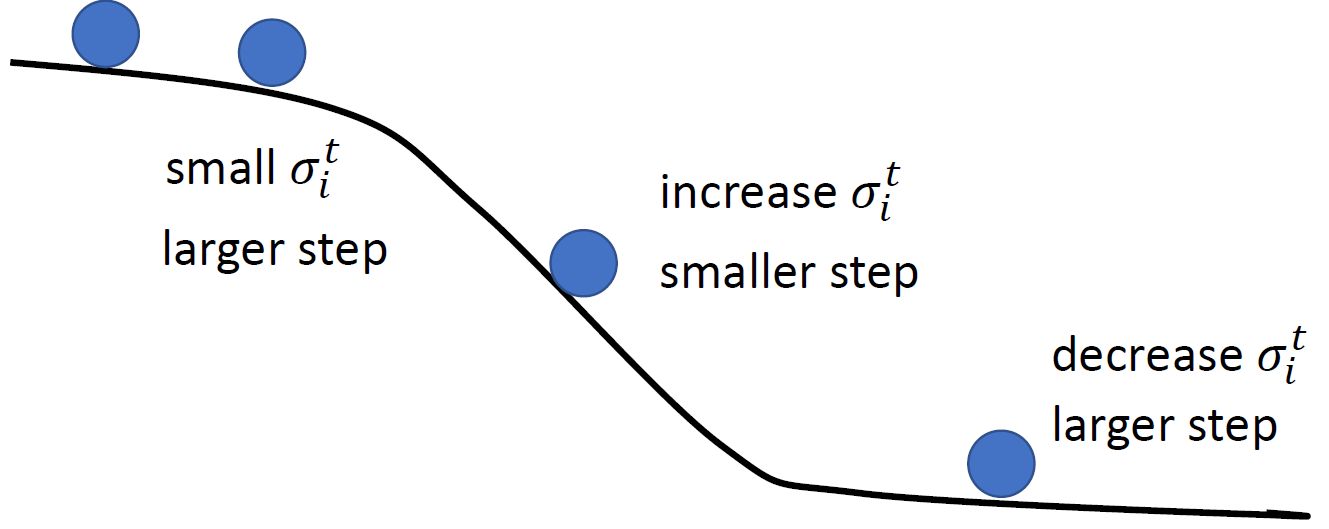图10：当陡峭程度不同时，在陡的地方会增加sigma，减少学习率。缓的地方反之
Adam
下图11所示为RMSprop的另一个改进版：Adam。
主要是有2个关键的变量： 
。
乘在了分子，相当于momentum，既考虑方向，又考虑大小。
乘在了分母上，相当于之前讨论的 
，只考虑方向，不考虑大小。
二者都是既考虑本次的梯度，也考虑之前的梯度。而此外的 
是超参数。这里解释为什么：
，前面time step 的 
可能比较小，所以我们想 
不那么小，就需要除以一个分数，让它变大一点。随着time step增加， 
变大，
变小，
变大，所以 
就比较稳定， 
同理。
图11：Adam
Adam
下图12所示为Adam的另一个改进版：AdamW。
简单来说，AdamW就是Adam优化器加上L2正则，来限制参数值不可太大，这一点属于机器学习入门知识了。以往的L2正则是直接加在损失函数上，比如这样子：加入正则，损失函数就会变成这样子：
所以在计算梯度 
时要加上粉色的这一项。
但AdamW稍有不同，如下图所示，将正则加在了绿色位置。
图12：AdamW
至于为何这么做？直接摘录BERT里面的原话看看：
Just adding the square of the weights to the loss function is not the correct way of using L2 regularization/weight decay with Adam, since that will interact with the m and v parameters in strange ways. Instead we want to decay the weights in a manner that doesn’t interact with the m/v parameters. This is equivalent to adding the square of the weights to the loss with plain (non-momentum) SGD. Add weight decay at the end (fixed version). 这段话意思是说，如果直接将L2正则加到loss上去，由于Adam优化器的后序操作，该正则项将会与
和
产生奇怪的作用。因而，AdamW选择将
正则项加在了Adam的
和
等参数被计算完之后、在与学习率
相乘之前，所以这也表明了weight_decay和
正则虽目的一致、公式一致，但用法还是不同，二者有着明显的差别。以BERT中的AdamW代码为例： ``` step_size = group[‘lr’] if group[‘correct_bias’]: # No bias correction for Bert bias_correction1 = 1.0 - beta1 state[‘step’] bias_correction2 = 1.0 - beta2 state[‘step’] step_size = step_size * math.sqrt(bias_correction2) / bias_correction1
p.data.addcdiv_(-step_size, exp_avg, denom)if group['weight_decay'] > 0.0:p.data.add_(-group['lr'] * group['weight_decay'], p.data)
``
如code，注意BERT这里的step_size就是当前的learning_rate。而最后两行就涉及weight_decay的计算。这一行大概是这样的：<br /><br />此处  就是weight_decay`。
下表是常用任务和模型的学习率自适应方式：
| SGD/SGDM | CV常用，ResNet，AdderNet |
|---|---|
| Adam/AdamW | NLP常用，Vision Transformer，GAN，Reinforcement learning |
learning rate scheduling
现在的另一个问题是：如图13所示，假设我们采用Root Mean Square的方法，那么当进行到后面梯度较小的时候，学习率会变得很大，导致参数的update出现振荡。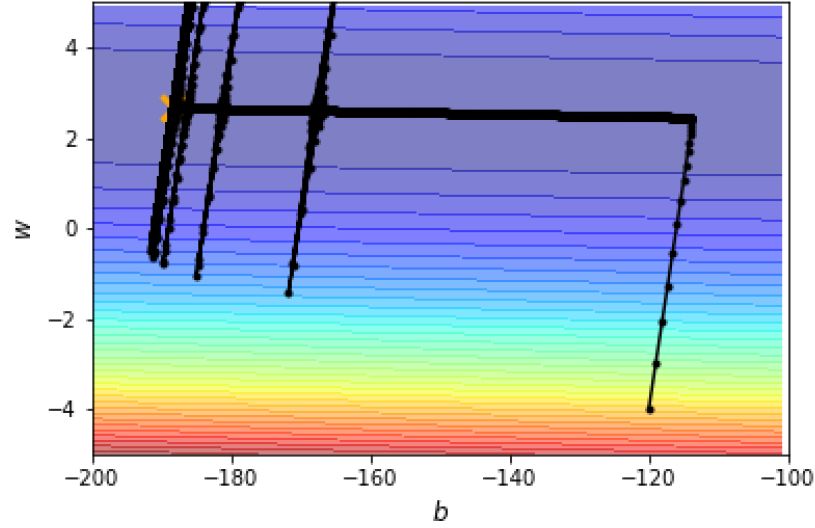
图13：参数的更新出现了振荡
所以这个时候就需要learning rate scheduling了。
在我们之前的更新中常采用：
当时的 
是不会随着时间变化而变化的。
那么现在learning rate scheduling采用：
那么该怎么和时间有关呢？
最常用的策略是learning rate decay，就是随着时间的进行，不断地减小。
这样得到的训练过程就比较正常了，如图14所示。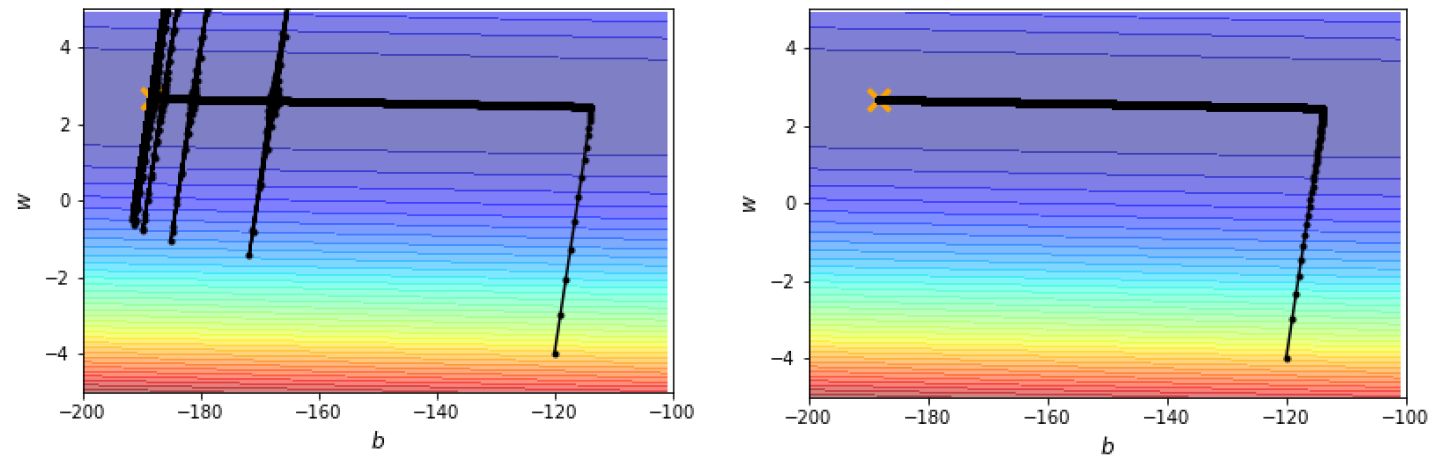
图14：learning rate decay避免了振荡
另一种办法是使用warm up的学习率调整策略，如图15所示。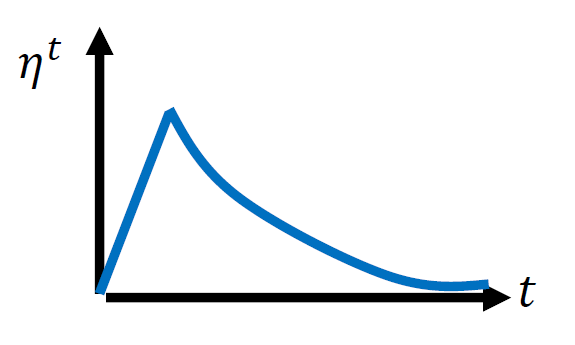
图15：warm up learning rate scheduling
为什么要这么做呢？有一个可能的解释是说：我们在计算 
的时候，它是个统计的结果，告诉我们某一个方向有多陡，或者多平滑。所以这个统计的结果，要看了足够多的数据以后，统计才精准。所以一开始的统计是不精准的，一开始的 
的计算是不准确的。所以我们一开始希望参数不离初始的地方太远。这也是一开始learning rate小的原因，先去探索，收集统计数据，再让learning rate慢慢拉升。
学习率和batchsize的关系
学习率和batchsize的关系应该是怎样的呢？
batchsize变大 
倍，学习率也要相应变大 
倍，本质是为了梯度的方差保持不变；
问：为什么要保证梯度的方差不变呢？
答：个人猜想，是为了解决陷入局部最优和一个sharp 最小值（类似于一个很尖的V底）的问题，增强泛化能力；增加了学习率，就增大了步长。
学习率直接影响模型的收敛状态，batchsize则影响模型的泛化性能。
学习率决定了权重迭代的步长，因此是一个非常敏感的参数，它对模型性能的影响体现在两个方面，第一个是初始学习率的大小，第二个是学习率的变换方案。
通常当我们增加batchsize为原来的 
倍时，要保证经过同样的样本后更新的权重相等，按照线性缩放规则，学习率应该增加为原来的 
倍。但是如果要保证权重的方差不变，则学习率应该增加为原来的 
倍，目前这两种策略都被研究过，使用前者的明显居多。
从两种常见的调整策略来看，学习率和batchsize都是同时增加的。学习率是一个非常敏感的因子，不可能太大，否则模型会不收敛。同样batchsize也会影响模型性能，那实际使用中都如何调整这两个参数呢？
衰减学习率可以通过增加batchsize来实现类似的效果，这实际上从SGD的权重更新式子就可以看出来两者确实是等价的，文中通过充分的实验验证了这一点。
对于一个固定的学习率，存在一个最优的batchsize能够最大化测试精度，这个batchsize和学习率以及训练集的大小正相关。
对此实际上是有两个建议：
- 如果增加了学习率，那么batch size最好也跟着增加，这样收敛更稳定。
- 尽量使用大的学习率，因为很多研究都表明更大的学习率有利于提高泛化能力。如果真的要衰减，可以尝试其他办法，比如增加batch size，学习率对模型的收敛影响真的很大，慎重调整。
若有收获，就点个赞吧
0 人点赞
