2113 - 从GAN到W-GAN的“硬核拆解”（二）：难训练的GAN

从GAN到W-GAN的“硬核拆解”（二）：难训练的GAN - 铁心核桃的文章 - 知乎 https://zhuanlan.zhihu.com/p/357141352

2014年，Goodfellow提出生成式对抗网络模型（GAN），该模型巧妙的以“水涨船高”的对抗方式交替训练判别器和生成器，逼着生成器不断提升造假水平，从而能够让其生成以假乱真的数据。GAN一诞生就风靡全球，广受追捧。但在对其新颖思路啧啧称奇的同时，“难训”也作为它的一个负面标签如影随形，使其广受争议，常常让使用者发出“理想很丰满，现实很骨感”的感叹。在这篇文章中，我们就来简单讨论这个问题。
希望对GAN原理做进一步了解的童鞋，戳下面的链接：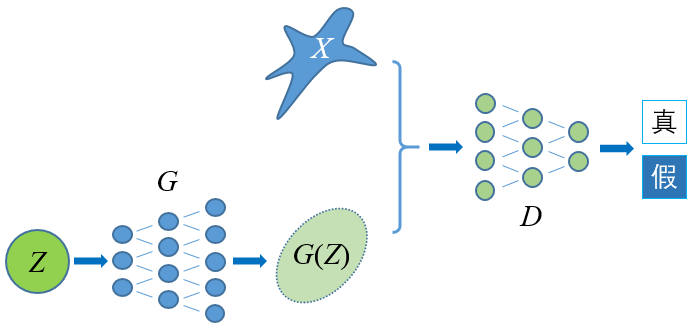

再说JS散度

在前面的文章中，我们多次介绍了常用作表示概率分布之间相似程度度量的KL散度（交叉熵）和JS散度（相对熵），在这两种散度中，JS散度又以其具有对称性的优势而更加常用。
一切看起来都很合理，但是实际有着致命的缺陷：具有指标性是度量函数的最基本要求，即输出值越小，则表示离二者越接近，反之亦反。但是JS散度的一个大问题即它存在饱和区间，一旦进入饱和区间，输出值即变为常数，丧失了度量分布相似程度能力。下面我们再从JS散度的定义式入手，看看所谓的“饱和区间”是怎么回事。
设和是两个待计算相似度的分布，二者之间的JS散度定义为

我们将 和分为3种情况进行讨论：

• 情况1：。这种情况无任何意义，记作；
• 情况2：（或）。两个分布无任何重叠区域，此时；

• 情况3：。两个分布有重叠区域，此时 。 对于上述情况2的“> ”问题，稍微做点不严密说明。JS散度计算的是在随机变量> 的取值区间上计算积分，而情况2表达的情况是所在> 的区间上，“有> 无> ，有> 无> ”的情况。由于JS散度的对称特性，我们只需考虑其中的一种情况，不妨假设> ，对于JS散度中的第一个KL散度项，有> 对于第二个KL散度项，有> （注：上面我们对的表述以及对的推导是不严密的，我们简单使的用了“”。准确的表述应该是“JS散度以为上界（upper bound）”。但是不管是直接等于还是以其为上界，都不影响我们分析JS散度作为分布相似度量存在的缺陷，我们只要知道JS无法“突破”就可以了）
  通过上面的分析，“”问题可以简单的描述为：

• 当时，；

• 当时，，当时，。

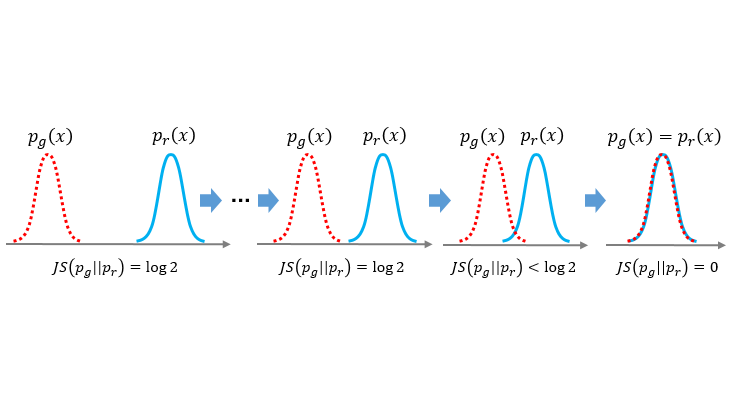
上面的两条特性可以用下面示意图像表示。
JS散度的饱和特性示意
这就意味着，对于和，只要两个分布没有交集，那么“不管远在天边还是近在眼前”，JS散度会认为他们一样的好坏，在这种情况下，JS散度进入所谓的饱和区间，丧失了度量两个分布相似程度的能力。

“纠结”的GAN优化

上一篇介绍GAN的文章中，我们经过一番推导后发现，GAN判别器的优化过程就是一个为生成器优化构造误差函数的过程，而构造的这个误差函数等价于生成数据分布与真实数据分布之间的JS散度。在随后的生成器优化过程即通过最小化这个JS散度，以使得逼近。我们再回顾一下GAN的生成器优化目标

具体在GAN的优化过程中，“”的饱和区间又意味着什么？简单来说，那真可谓是“有一个好消息，还有一个坏消息”：

• 好消息：两个分布完全无重叠，则一定存在一个最优分类器，能够使得对两种分布样本的分类精度达到100%。也就是说在GAN的判别器优化过程中，那个我们心心念念寻找的完美判别器是一定存在的，我们放开手去找就是了；
• 坏消息：JS作为损失函数输出为常数，即梯度为0，意味着我们在优化生成器时，梯度下降法将不知道朝哪个方向下降。

判别器越接近最优，优化目标则越近似于最小化和间的JS散度，若和间无重叠或是重叠小到可忽略不计，生成器因为“”问题将越有可能无法进行梯度下降。即所谓的“判别器越优，生成器越难训”。
那么我们不禁要问了，和不重叠的情况多吗？回答很令人失望：特别多，多到“不重叠”这件事是一个必然事件。有这么一条定理在说这件事情： 当> 与> 的支撑集是高维空间中的低维流形时，> 与> 重叠部分测度为0的概率为1. 首先看第一句，现代机器学习都认为同类自然数据是高维空间中的低维流形，即满足流形分布律（假如像素的人脸图像，我们都用3个姿态角来表达，我们就说人脸图像是嵌入在维空间中的3维流形）。至于第二句，翻译成人话就是能用低维表达的两组数据，放在高维空间中、用高维空间的度量方式测算他们分布的重叠度，则他们没有重叠的可能。所谓的测度就是一维的长度、二维的面积、三维的体积…等等。我们用下面三个图示表示上面的定理，一目了然
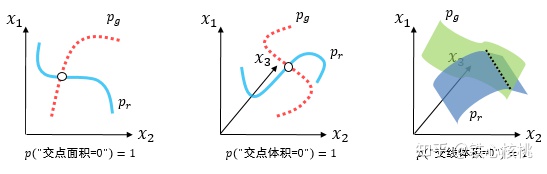对上述“必然事件定理”的一个图示说明（从左至右为嵌入2维空间的1维流形、嵌入3维空间中的1维流形和嵌入3维空间中的2维流形）
特别地，在GAN训练的初期，生成的数据和真实的数据肯定不像（要是像了我们还训练啥？直接生成不就得了？），即和重叠度很低，一旦我们得到了一个火眼金睛的“检验员”能一眼看出真伪，那后面“造假者”就再也没有历练的机会了。这下我们就纠结了：一方面我们要训练一个最优的判别器，以它作为一个强大对手来历练判别器；但是另一方面一旦有最优判别器在手，我们生成器就“掉进坑里，再也爬不上来”。

“原生”改进——“The −log D alternative”

上文我们已经介绍，JS散度作为GAN生成器的优化目标是存在问题的，尤其是在GAN的训练初期，生成的假数据还处于“瞎蒙”时，这个问题是致命的，一句话表示就是“训练初期无梯度可用”。GAN的作者Goodfellow大牛自然也认识到这一点，在提出GAN的论文中（注：这就是所谓“原生”的意思）提出一种叫做“The −log D alternative”（下面简称为“-log方案”）的技巧，希望GAN在训练初期具有更加强劲的梯度可用。我们简单的分析Goodfellow的做法是否能够解决JS散度的问题。
在获得最优判别器后，GAN最原始的生成器优化目标函数为

Goodfellow的“-log方案”将上式改写为

不难看出，以上两个式子具有相同的优化结果。我们将上面两个对数函数的曲线绘制出来可以看出，GoodFellow提出的“-log方案”，其曲线在靠近0的地方更加陡峭，即表明在GAN的训练初期的确具有更加强有力的梯度。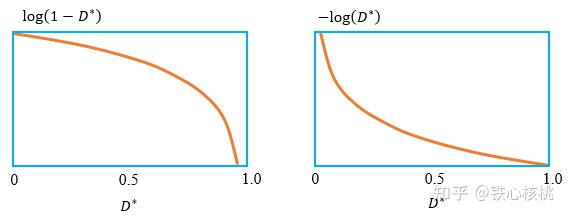
原方案 vs. “-log方案”
我们不禁要问，开始时梯度是大了，但是“-log方案”彻底解决了JS散度的问题吗？我们再简单进行一下分析。首先我们对KL散度做一点变形

上面的式子“截取两头”，有

对上式移项，有

而在GAN的目标函数分析中，我们还知道

和 (1) 式放在一起整理，有

这里我们是优化生成器，而“{}”中的内容与无关，所以在计算的时候可以忽略。因此“-log方案”的散度等价形式为

上面的式子除了类似饱和区间的问题外，还存在着两个严重的问题：

• 梯度不稳定：我们说KL散度和JS散度具有类似的性质，都可以表达分布的相似程度，即当时，和越接近，二者都越趋近0，但是这里竟然同时出现“+”和“-”，一个要拉近，一个要推远，造成梯度不稳定——“左边拉我右边拽我，我只好左躲右闪”；
• 丧失多样性：，导致惩罚力度不一致，造成生成器放弃生成样本的多样性（“崩塌模式”，collapse mode）——“一会儿棒子一会儿酸枣，我只好选个自己最舒服的状态保持下去”。

关于KL散度不对称导致惩罚力度不一致的问题，我们再举一个例子说明。先看下面的两幅图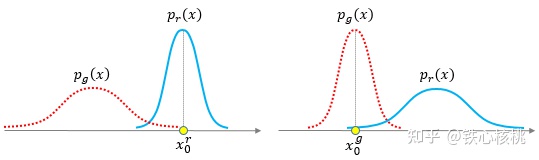
“像的生成不了” vs. “能生成的不像”

• 左图——“像的生成不了”：真实样本都集中在附近，但在此处几乎没分布，表明生成器无法生成与之相似的样本，这种情况下

• 右图——“能生成的不像”：能生成的样本都集中在附近，但在此处几乎没分布，表明生成的样本与真实样本很不相似，这种情况下

我们按照“人类正常的思绪”来看，“像的生成不了”和“能生成的不像”实际表达的都是“生成器烂”这一件事儿，但是KL散度却给出了截然相反的两种惩罚结果——一个“挠痒痒”（左图）和一个“往死打”（右图）。且不说KL散度和JS散度一正一负的问题，光KL散度自己都能惹出如此的事端来，看来“-log方案”更不咋地。

结束语

GAN的难训练是出了名的，这篇文章我们对这一问题底层原因进行了分析——归根结底出在分部间相似性度量上。无论是最初的优化目标还是GoodFellow大神亲自出手给出的“-log方案”统统不行，看来问题已经深入骨髓了。既然问题出在度量上，那我们就换一个度量。下一篇文章我们将放弃基于散度的分布相似性度量方案，祭出我们期待已久的沃瑟斯坦（Wasserstein）距离。