池化层

池化运算：对信号进行“收集”并“总结”，类似水池收集水资源，因而得名池化层
“收集”：多变少
“总结”：最大值/平均值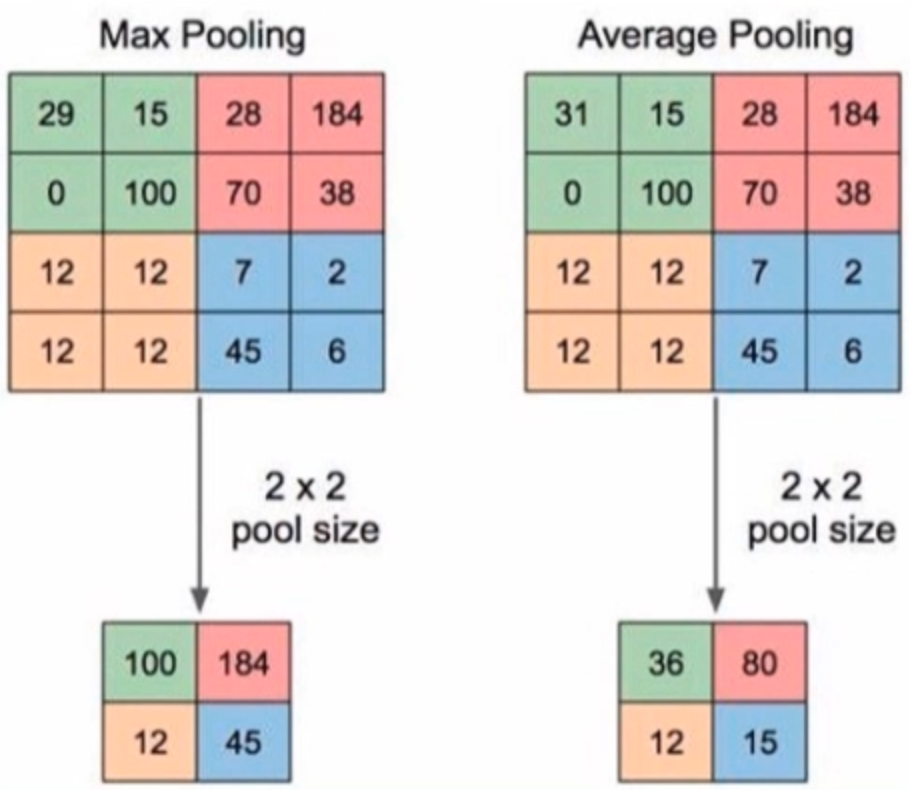

左边是最大池化，右边是平均池化

nn.MaxPool2d

功能：对二维信号（图像）进行最大值池化
主要参数：

• kernel_size：池化核尺寸
• stride：步长（通常与kernel_size一样大，就是不重叠）
• padding：填充个数
• dilation：池化核间隔大小
• ceil_mode：尺寸向上取整
• return_indices：记录池化像素索引（通常是在最大值反池化上采样时使用,）

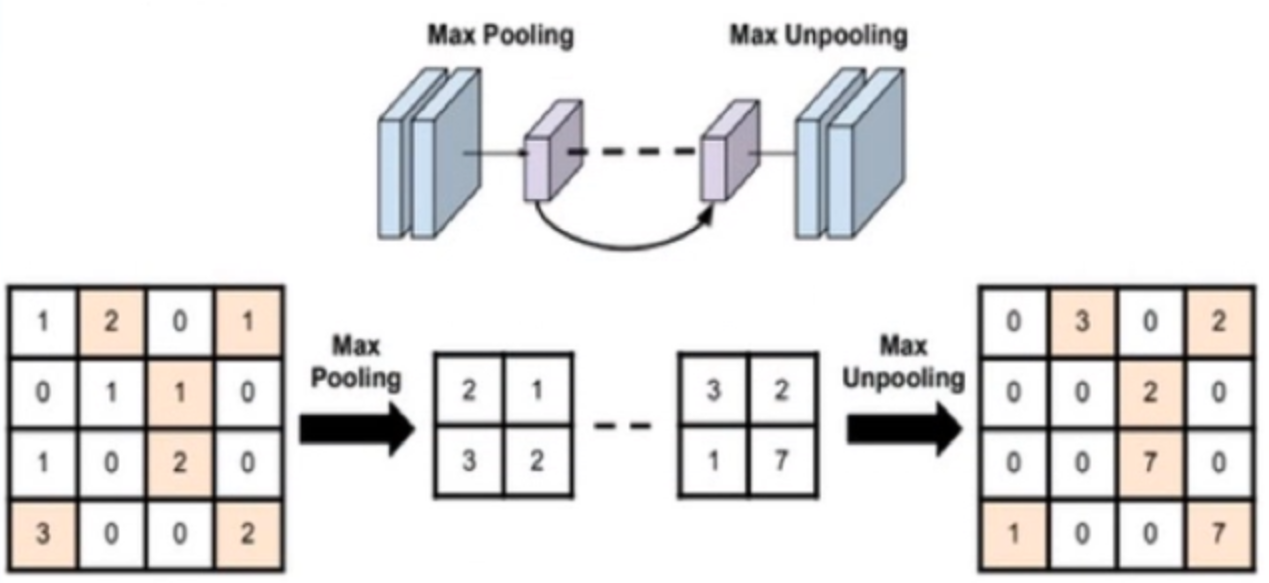
最大值反池化上采样，将最大值映射到原来的位置上

代码实现

maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2))#input:(i, o, size) weights:(o, i, h, w)
img_pool = maxpool_layer(img_tensor)

因为是2d池化，所以kernel_size和stride都要设置两个方向的。将池化后的结果可视化如下：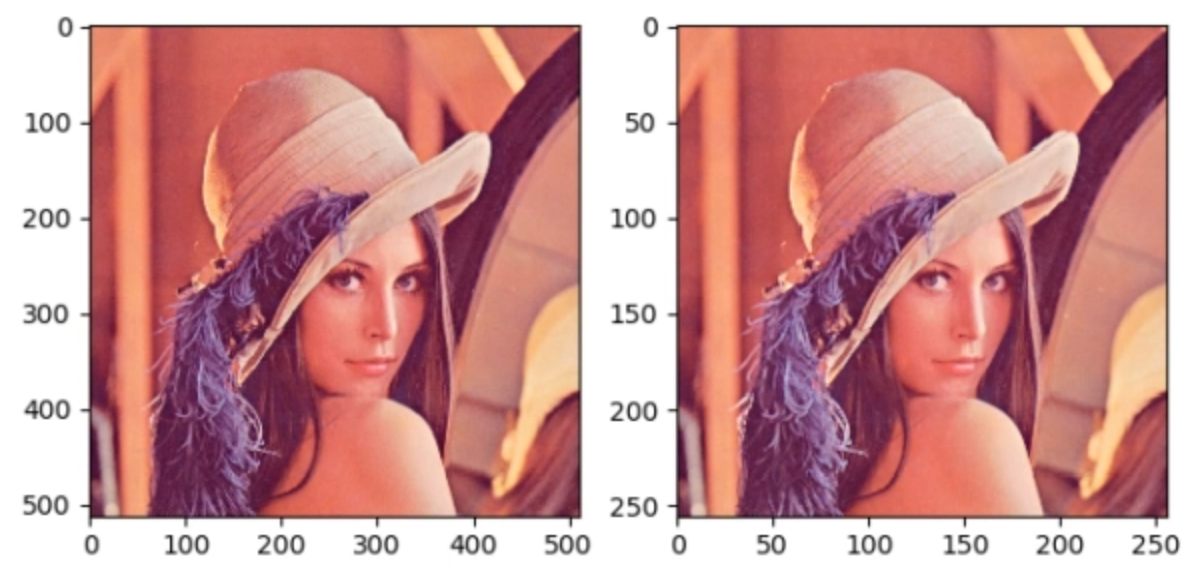

可以看到图像尺寸缩小一半，但质量并没有什么差别，因此池化可以实现冗余信息的剔除，以及减小后面的计算量。

nn.AvgPool2d

功能：对二维信号（图像）进行平均值池化
主要参数：

• kernel_size：池化核尺寸
• stride：步长
• padding：填充个数
• ceil_mode：尺寸向上取整
• count_include_pad：填充值用于计算
• divisor_override：除法因子（设置后不再除以池化核尺寸的大小，而是除法因子，也就是自定义分母）

代码实现

avgpoollayer = nn.AvgPool2d((2, 2), stride=(2, 2))   # input:(i, o, size) weights:(o, i , h, w)
img_pool = avgpoollayer(img_tensor)

平均池化后的可视化结果如下：

对比上面最大池化的可视化结果，可以看到这里会更暗淡。因为最大池化取到的像素值都是最大的，所以更鲜艳。

nn.MaxUnpool2d

功能：对二维信号（图像）进行最大值池化上采样
主要参数：

• kernel_size：池化核尺寸
• stride：步长
• padding：填充个数

使用方法与MaxPool差不多，就是在之前下采样时要记录最大值的索引，然后在forward的时候传入index参数。

代码实现

# pooling
img_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float) # 构建池化的输入数据
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True) # 创建池化层
img_pool, indices = maxpool_layer(img_tensor) # 注意这里返回最大值索引
# unpooling
img_reconstruct = torch.randn_like(img_pool, dtype=torch.float) # 创建反池化的输入数据
maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2)) # 创建反池化层
img_unpool = maxunpool_layer(img_reconstruct, indices) # 注意这里加入indices参数

线性层

线性层又称全连接层，其每个神经元与上一层所有神经元相连实现对前一层的线性组合，线性变换。

nn.Linear

功能：对一维信号（向量）进行线性组合
主要参数：

• in_features：输入结点数
• out_features：输出结点数
• bias：是否需要偏置

计算公式：

代码实现

inputs = torch.tensor([[1., 2, 3]]) # 构建输入数据
linear_layer = nn.Linear(3, 4) # 构建线性层
linear_layer.weight.data = torch.tensor([[1., 1., 1.],
                                         [2., 2., 2.],
                                         [3., 3., 3.],
                                         [4., 4., 4.]])  
    # 构建weight，这里每一行代表神经元与前一层连接的权值。
linear_layer.bias.data.fill_(0.5)
output = linear_layer(inputs)

激活函数层

激活函数对特征进行非线性变换，赋予多层神经网络具有深度的意义。
若没有非线性激活函数，那么无论多少层神经网络，都可以看作是一个线性函数而已。

常用激活函数

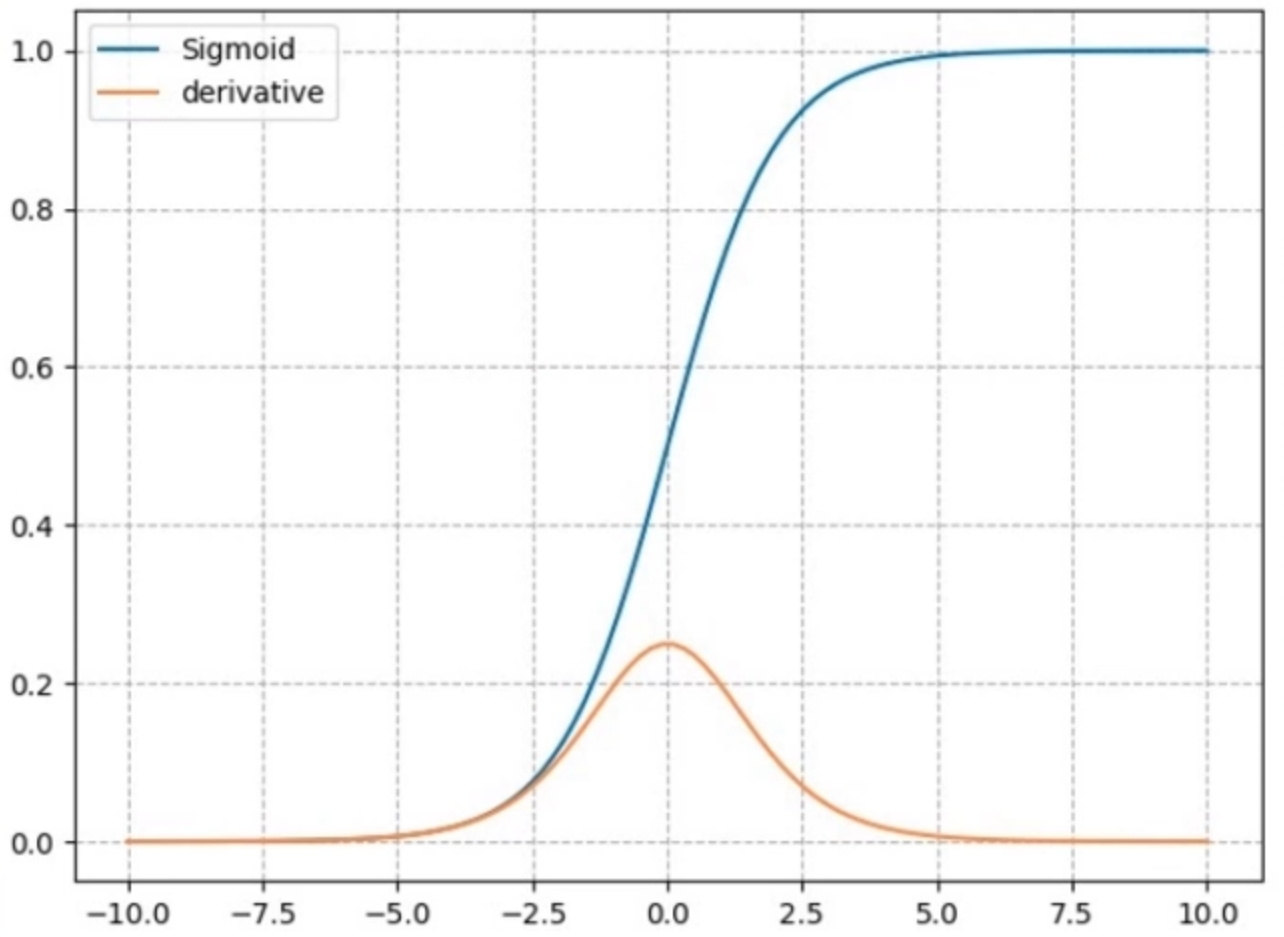
nn.Sigmoid

计算公式：
梯度公式：
特性：

1. 输出值在(0，1)，符合概率
2. 导数范围是[0，0.25]，在根据链式法则计算梯度时需要乘以激活函数的导数，会使梯度变小，易导致梯度消失
3. 输出为非0均值，会破坏数据的0均值分布

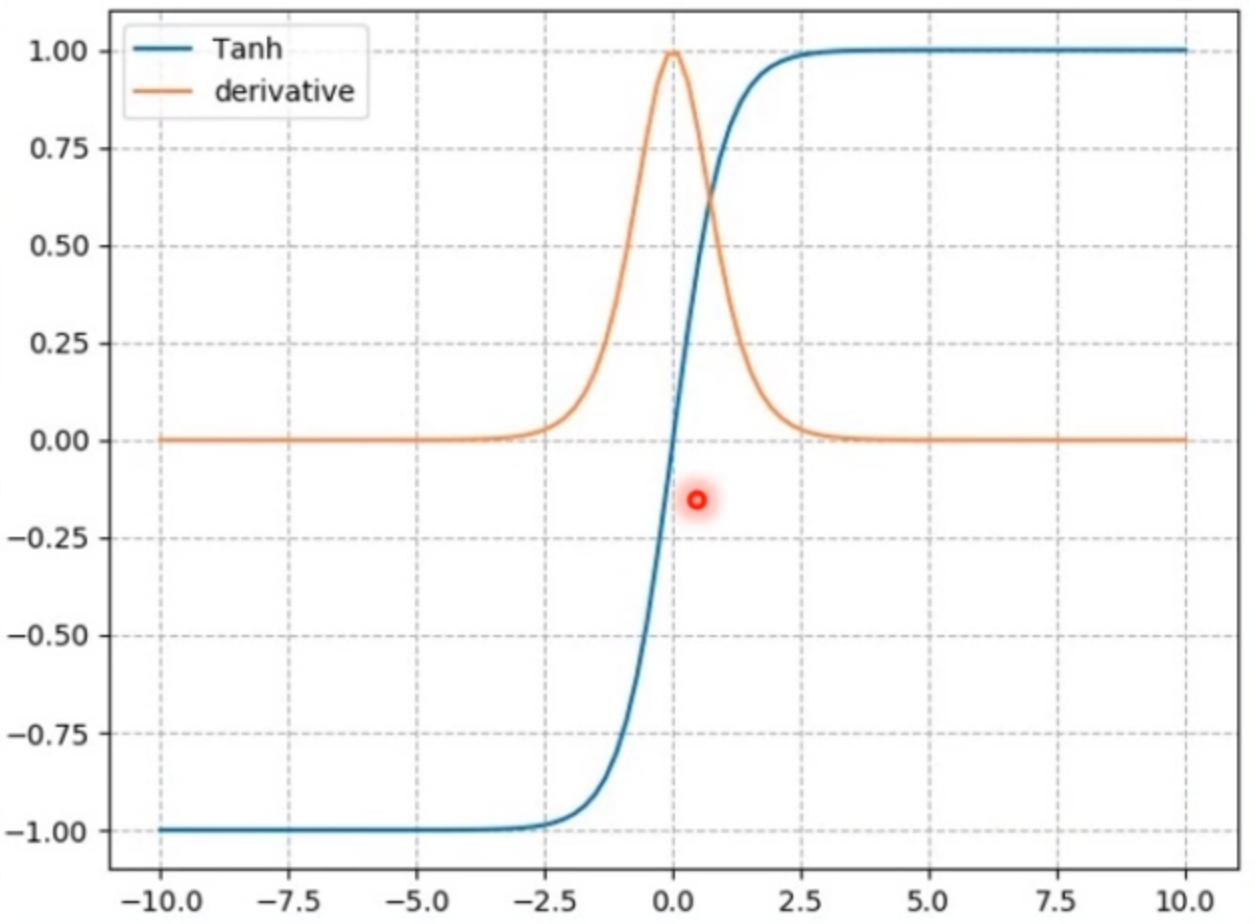
nn.tanh

计算公式：
梯度公式：
特性：

1. 输出值在(-1，1)，数据符合0均值
2. 导数范围是(0，1)，易导致梯度消失，但没有Sigmoid那么严重

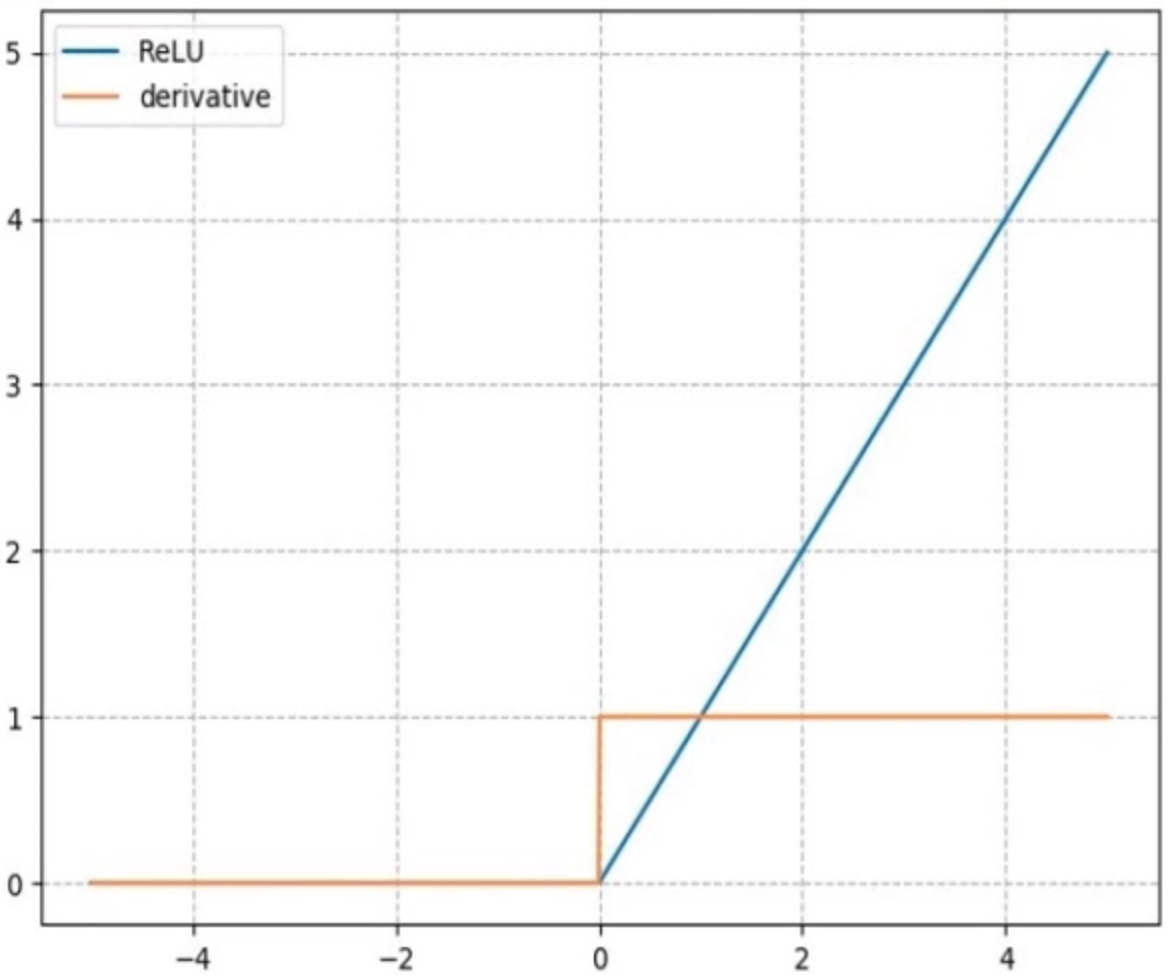
nn.ReLU

计算公式：
梯度公式：
特性：

1. 输出值均为正数，负半轴输出都为0，会导致死神经元现象
2. 导数是1，缓解梯度消失，但易引发梯度爆炸。因为在链式求导时不会减小梯度。

针对ReLu死神经元的问题，有很多改进措施：

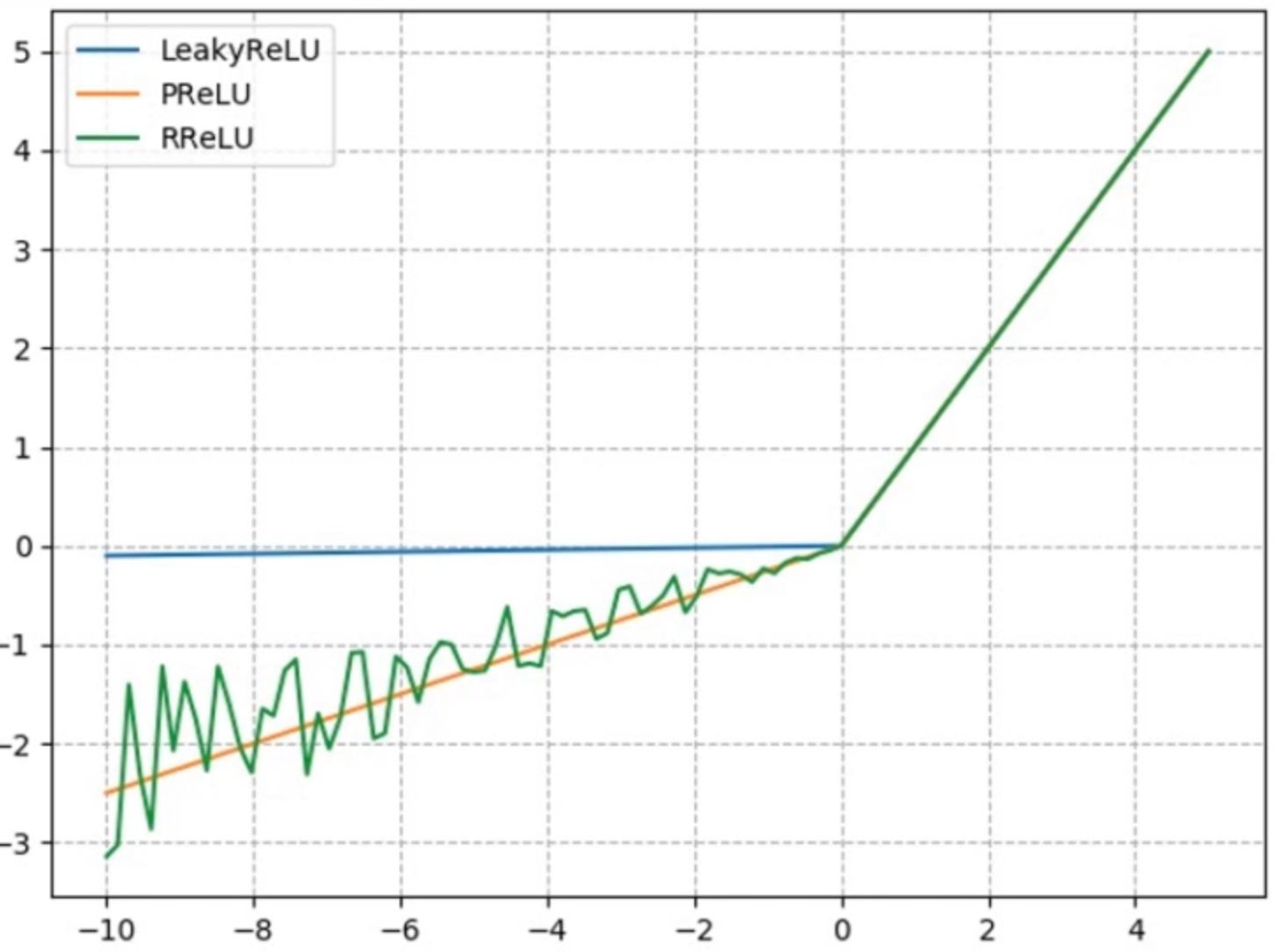
nn.LeakyReLU

给负半轴一个固定的斜率

• negative_slope：负半轴斜率

  nn.PReLU

  斜率是可学习的

• init：可学习斜率（初始化）

  nn.RReLU

  负半轴的斜率是从均匀分布中随机采样的

• lower：均匀分布下限

• upper：均匀分布上限