概念

pytorch的优化器：管理并更新模型中可学习参数（weight、bias等）的值，使得loss降低，从而模型输出更接近真实标签。

导数：函数在指定坐标轴上的变化率
方向导数：指定方向上的变化率
梯度：是一个向量，其方向是使方向导数取得最大值的方向，其模长是增长的变化率

基本属性

• defaults：优化器超参数
• state：参数的缓存，如momentum的缓存
• param_groups：管理的参数组。这是一个list，其中每个元素是一个字典。字典中有个key为’params‘的value又是一个list，里面存放的就是模型中的每一个可学习参数。字典中还存放了lr、momentum等超参数。
• _step_count：记录更新次数，学习率调整中使用

基本方法

zero_grad()

功能：功能清空所管理参数的梯度
pytorch特性：张量梯度不自动清零，而会一直迭加。所以需要手动设置清零。

step()

功能：在backward得到grad后，执行一步更新

add_param_group()

功能：当要分段训练的时候就要为每个分段分别定义不同的参数组。例如把整个网络分为特征提取和分类两部分，前面特征提取部分的学习率设置低一点，后面全连接层的学习率设置高一点。

注意param_group是一个list，其中一个字典表示一组参数组。所以该函数接收的是一个字典。

w2 = torch.randn((3, 3), requires_grad=True)
optimizer.add_param_group({"params": w2, 'lr': 0.0001})

模型训练状态的保存和加载：

state_dict（）

功能：获取优化器当前状态信息字典

optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
opt_state_dict = optimizer.state_dict()
print("state_dict before step:\n", opt_state_dict)
for i in range(10):
    optimizer.step()
print("state_dict after step:\n", optimizer.state_dict())
torch.save(optimizer.state_dict(), os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))

在模型训练一定间隔后保存当前状态信息为pkl文件，当意外中止训练时可以加载pkl的状态信息从断点继续训练。

load_state_dict（）

功能：加载状态信息字典

optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
state_dict = torch.load(os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))
print("state_dict before load state:\n", optimizer.state_dict())
optimizer.load_state_dict(state_dict)
print("state_dict after load state:\n", optimizer.state_dict())

将pkl加载为state_dict后，再将load_state_dict进optimizer中。

这两个方法是为了模型训练中断后继续训练。所以可以在模型训练一定间隔后保存一次当前状态信息，当意外终止训练时可以恢复训练。

代码实现流程

第一步 选择优化器

optimizer = optim.SGD(net.parameters(), lr=LR, momentum=0.9)

1.1 进入SGD类的init初始化，判断超参数输入是否合法，然后进入基类optimizer的init函数
1.2 在optimizer的init函数中初始化defaults, state, param_groups，然后将模型参数net.parameters()加入到 param_groups中。
1.3 完成初始化后，param_groups中就有一个字典，字典中key为params的value是一个list，里面保存的就是模型可学习参数，包含了各网络层的weight和bias。

第二步 训练模型

2.1 前向传播

inputs, labels = data
outputs = net(inputs)

2.2 反向传播

optimizer.zero_grad()  # 清空梯度
loss = criterion(outputs, labels)  # 计算loss
loss.backward()    # 自动求导grad

2.3 权重更新

optimizer.step()

因为optimizer的params_group中已经存了模型参数的地址，所以可以找到模型参数的grad从而更新参数。

学习率

作用：控制更新的步伐（尺度），避免loss的激增和梯度爆炸。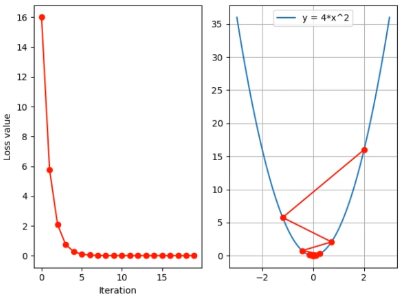

注意：一般无法直接找到最好的学习率，所以一般选择比较小的值，让loss慢慢降低，用时间来弥补。但也不能设置过小，否则要花费很长很长的时间。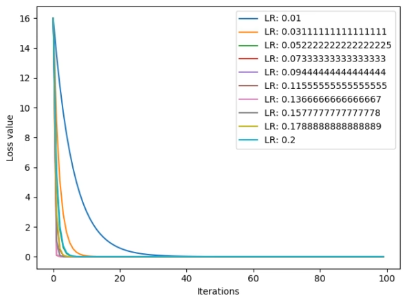

Momentum

作用：结合当前梯度与之前的更新信息，用于当前更新。其中，距离当前更新越近的更新信息影像权重越大，距离越远的更新信息影像权重越小。

指数加权平均

计算公式为：

其中，表示当前时刻的平均值，表示当前时刻参数，是超参数（小于1），是上一时刻的平均值。
该公式表示当前时刻的平均值，除了要考虑当前时刻的数据以外，还要考虑之前的均值对当前时刻的均值的影响，并且越靠近当前时刻的历史数据对当前时刻平均值的影响越大，之前的历史参数对当前参数的影响因子呈指数变化。证明如下：
将上面的式子不断迭代展开用来表示：

观察系数，由于，所以是指数下降的，越早时刻的数据的系数越小，也就是影响的权重越小；反之越近时刻的数据影响越大。

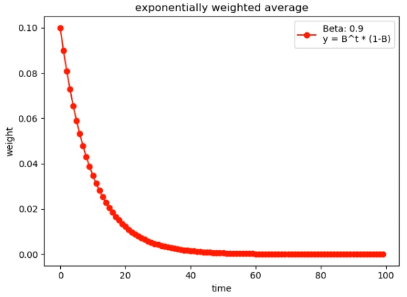
对超参调节可以发现，越小，对历史信息的记忆周期越短。例如当时，20个时刻以前的权重已经无法对当前时刻的平均值造成什么影响了。

注意：通常设置为0.9，表示更关注距离当前10个时刻之内的历史信息。计算公式为：

Momentum原理

在Pytroch中，动量梯度下降的公式为：


其中，
表示第i+1次更新的参数；
表示更新量；
m表示Momentum系数，与上面的超参数类似
表示的梯度。

举个例子辅助理解，将的式子展开：

与指数加权平均的思想一样，离当前更新越早的梯度的影响权重呈指数下降。

作用：考虑之前的更新信息，如果之前梯度下降的方向与当前方向一致，那么就可以加速loss的降低。

torch.optim.SGD

主要参数：

• params：管理的参数组
• Ir：初始学习率
• momentum：动量系数，贝塔
• weight_decay:L2正则化系数
• nesterov：是否采用NAG，默认是false

NAG参考文献：《On the importance of initialization and momentum in deep learning》

PyTorch的十种优化器

1.optim.SGD：随机梯度下降法（适用90%模型上）
2.optim.Adagrad：自适应学习率梯度下降法
3.optim.RMSprop:Adagrad的改进
4.optim.Adadelta:Adagrad的改进
5.optim.Adam:RMSprop结合Momentum
6.optim.Adamax:Adam增加学习率上限
7.optim.SparseAdam：稀疏版的Adam
8.optim.ASGD：随机平均梯度下降
9.optim.Rprop：弹性反向传播（所有样本直接参与计算的时候用，分batch时不用）
10.optim.LBFGS:BFGS的改进（L代表limit）
参考文献：
1.optim.SGD:《On the importance of initialization and momentum in deep learning》
2.optim.Adagrad:《Adaptive Subgradient Methods for Online Learning and Stochastic
Optimization》
3.optim.RMSprop：
http://www.cs.toronto.edu/-tijmen/csc321/slides/lecture_slides_lec6.pdf
4.optim.Adadelta:《AN ADAPTIVE LEARNING RATE METHOD》
5.optim.Adam:《Adam:A Method for Stochastic Optimization》
6.optim.Adamax:《Adam:A Method for Stochastic Optimization》
7.optim.SparseAdam
8.optim.ASGD:《Accelerating Stochastic Gradient Descent using Predictive Variance
Reduction》
9.optim.Rprop:《Martin Riedmiller und Heinrich Braun》
10.optim.LBFGS:BDGS的改进