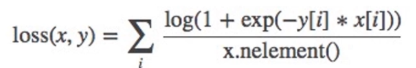- 概念
- Pytorch的损失函数
- 1. nn.CrossEntropyLoss
2. nn.NLLLoss- 3. nn.BCELoss
- 4. nn.BCEWithLogitsLoss
- 5. nn.L1Loss
- 6. nn.MSELoss
- 7. nn.SmoothLlLoss
- 8. nn.PoissonNLLLoss
- 9. nn.KLDivLoss
- 10. nn.MarginRankingLoss
- 11. nn.MultiLabelMarginLoss
- 12. nn.SoftMarginLoss
- 13. nn.MultiLabelSoftMarginLoss
- 14. nn.MultiMarginLoss
- 15. nn.TripletMarginLoss
- 16. nn.HingeEmbeddingLoss
- 17. nn.CosineEmbeddingLoss
- 18. nn.CTCLoss
概念
损失函数:衡量模型输出与真实的标签之间得到差距,关键在定义了如何衡量单样本输出与真实间差距的函数;
代价函数:总体样本与真实间的差距。
目标函数:在最小化代价函数的基础上,还要用正则项起一些约束。
Pytorch的损失函数

注意:
- size_average和reduce参数在Pytroch新版本中去掉了,因为两者均可以由reduction实现。
- Loss继承于Module
- Loss类的init方法中就是设置reduction参数
1. nn.CrossEntropyLoss
功能:nn.LogSoftmax()与nn.NLLLoss()结合,进行交叉熵计算,这里的target中的变量类型是long
主要参数
- weight:各类别的loss设置权值,设置权值后求均值是按加权求均值
- ignore_index:忽略某个类别
- reduction:计算模式,可为none/sum/mean
- none-逐个元素计算
- sum-所有元素求和,返回标量
- mean-加权平均,返回标量
注意这个函数并不是数学公式意义上的交叉熵函数。它的不同之处在于这里使用Softmax将输出数据归一化为概率输出。因为交叉熵通常用于分类任务,而分类任务中通常输出概率值,所以交叉熵是用来衡量两个概率分布的差异。交叉熵越低,则这两个概率分布越接近。
那么为什么交叉熵越低,概率分布越接近,这就要来看相对熵的概念:
熵
是用来描述事件的不确定性。某个事件越不确定,它的熵越大。
用数学公式表示就是自信息的数学期望:
那么下面来看看什么是自信息:
自信息
自信息是用来衡量单个事件的不确定性:
也就是对单个事件发生的概率p(x)求负log。
而信息熵是描述整个概率分布的不确定性,所以要对自信息求期望。
下面举个例子来看看熵的大小与事件不确定性的关系: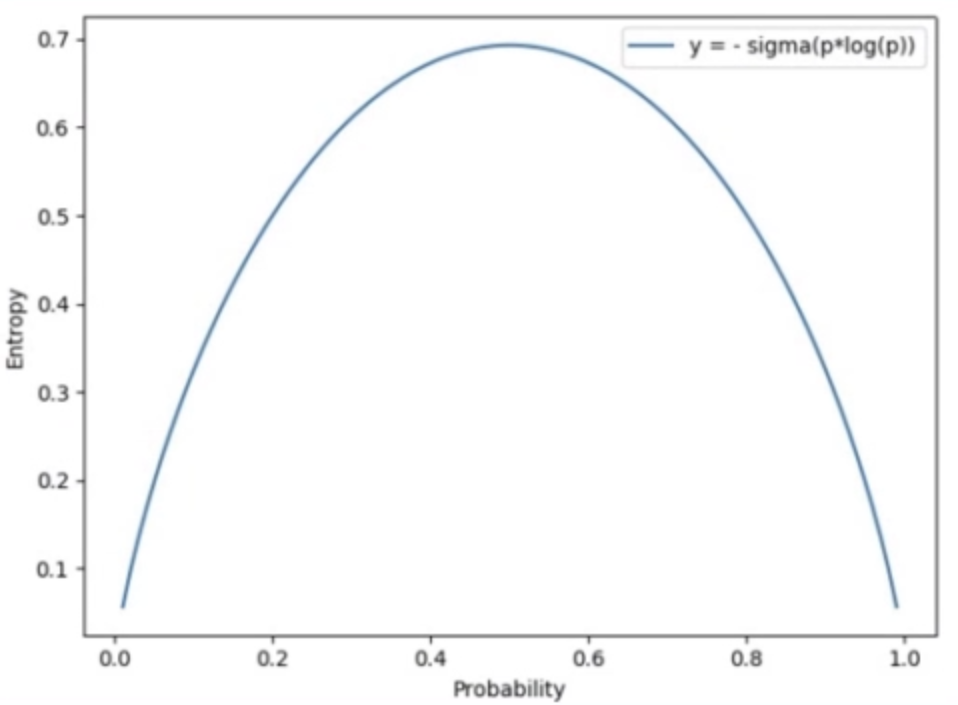
这是两点分布的信息熵,可以看到当事件概率为0.5时,不确定性最大,即信息熵最大,为0.69。这个数字很常见,在训练二分类模型第一个iteration时Loss基本就是0.69,表明此时模型对任何输出的判别概率都为0.5(可能或不可能)。
相对熵(KL散度)
被用来衡量两个分布之间的差异:
但注意它不是一个距离函数,因为距离函数具有对称性:P到Q的距离等于Q到P的距离。但相对熵公式中P表示真实分布,Q表示模型输出的分布,这里需要将Q去拟合P的真实分布,所以不具有对称性。
将公式展开如下:
交叉熵
用来衡量两个分布之间的相似度:
所以我们发现有关系如下:
交叉熵=信息熵+相对熵
即:
这里P是输入的真实分布,Q是模型输出的分布。所以H(P)是常数,所以在模型训练时优化交叉熵就相当于优化相对熵。
Pytorch中计算交叉熵
对比交叉熵的数学公式:
此时假设只计算一个x样本,因为x的类别已经确定,所以,上式也就转化为
由于模型输出不会服从概率分布的形式,所以这里用softmax将模型输出x[class]归一化为概率分布(01区间)
所以交叉熵损失函数可以计算如下:
如果参数设置weight后,计算公式如下:
也就是在计算某个类别的loss时乘上一个权重
手动实现
就是用numpy实现数学公式
inputs = torch.tensor([[1, 2], [1, 3], [1, 3]], dtype=torch.float) # 构造输出值target = torch.tensor([0, 1, 1], dtype=torch.long) # 构造labelidx = 0 # 计算第一个样本的lossinput_1 = inputs.detach().numpy()[idx] # [1, 2]target_1 = target.numpy()[idx] # 0# 第一项x_class = input_1[target_1] # 第一个神经元的输出值# 第二项sigma_exp_x = np.sum(list(map(np.exp, input_1))) # 对所有输出值求e的指数函数再求和log_sigma_exp_x = np.log(sigma_exp_x)# 输出lossloss_1 = -x_class + log_sigma_exp_x
当设置weight参数时,计算mean模式的loss:
weights = torch.tensor([1, 2], dtype=torch.float) #先给每个类别设置一个weightweights_all = np.sum(list(map(lambda x: weights.numpy()[x], target.numpy())))# 把每个target.numpy()的值[0, 1, 1] 代入算出每个loss的权重为 [1 2 2],最后求和为5mean = 0loss_sep = loss_none.detach().numpy() # 这里是把之前计算的none模型的loss转为numpyfor i in range(target.shape[0]):x_class = target.numpy()[i]tmp = loss_sep[i] * (weights.numpy()[x_class] / weights_all) #计算每个loss占的比重mean += tmpprint(mean)
注意:设置weight参数计算mean模式的loss时,要除以loss权重的份数,而不是样本数。
自动实现
使用pytroch提供的CrossEntropyLoss函数:
weights = torch.tensor([1, 2], dtype=torch.float)# weights = torch.tensor([0.7, 0.3], dtype=torch.float)loss_f_none_w = nn.CrossEntropyLoss(weight=weights, reduction='none')loss_f_sum = nn.CrossEntropyLoss(weight=weights, reduction='sum')loss_f_mean = nn.CrossEntropyLoss(weight=weights, reduction='mean')# forwardloss_none_w = loss_f_none_w(inputs, target)loss_sum = loss_f_sum(inputs, target)loss_mean = loss_f_mean(inputs, target)# viewprint("\nweights: ", weights)print(loss_none_w, loss_sum, loss_mean)
代码实现流程
第一步 初始化CrossEntropyLoss类
loss_functoin = nn.CrossEntropyLoss()
1.1 进入CrossEntropyLoss的init方法执行其基类_WeightedLoss**的init方法
def __init__(self, weight=None, size_average=None, ignore_index=-100,reduce=None, reduction='mean'):super(CrossEntropyLoss, self).__init__(weight, size_average, reduce, reduction)self.ignore_index = ignore_index
1.2 进入_WeightedLoss的init方法执行其基类_Loss的init方法
class _WeightedLoss(_Loss):def __init__(self, weight=None, size_average=None, reduce=None, reduction='mean'):super(_WeightedLoss, self).__init__(size_average, reduce, reduction)self.register_buffer('weight', weight)
1.3 进入_Loss的init方法执行其基类Module的init方法,也就是创建8个有序字典。因为Loss是一个最基本的层,没有子网层也没有参数,所以有序字典中都是空的。
第二步 用来衡量outputs和label的差异
在模型forward得到输出值后:
# forwardinputs, labels = dataoutputs = net(inputs)# backwardoptimizer.zero_grad()loss = loss_functoin(outputs, labels)loss.backward()
2.1 因为CrossEntropyLoss是Module子类,所以此时调用Module的call方法
2.2 Module的call方法中调用了forward方法
2.3 进入CrossEntropy类中的forward方法,调用F.cross_Entropy方法。F是nn模块的一个function,里面有很多函数,CrossEntropy的计算就是在这里面实现的。
def forward(self, input, target):return F.cross_entropy(input, target, weight=self.weight,ignore_index=self.ignore_index, reduction=self.reduction)
2.4 进入functional.py的cross_Entropy函数,里面就是先判断reduction模式,然后通过nn.NLLLoss和log_softmax计算交叉熵。
if size_average is not None or reduce is not None:reduction = _Reduction.legacy_get_string(size_average, reduce)return nll_loss(log_softmax(input, 1), target, weight, None, ignore_index, None, reduction)
2. nn.NLLLoss
功能:实现负对数似然函数中的负号功能(其实就是求负数)
主要参数:
- weight:各类别的loss设置权值
- ignore_index:忽略某个类别
- reduction:计算模式,可为none/sum/mean
- none-逐个元素计算
- sum-所有元素求和,返回标量
- mean-加权平均,返回标量
3. nn.BCELoss
功能:二分类交叉熵
注意事项:
- 输入值取值在[0,1],所以常常需要在最后加上Sigmoid函数
- 这里是输出层每个神经元一一对应计算loss,而不是像在CrossEntropyLoss中是一整个输出层向量去计算loss。
- label的类型为torch.float,CrossEntropyLoss中是torch.long
这里就是数学公式意义上的交叉熵: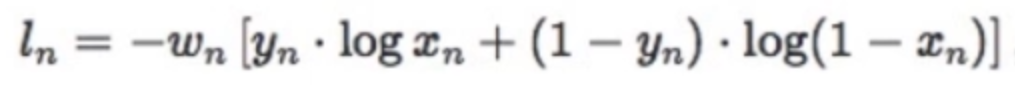
其中,x是输出值,y是label
主要参数**:
- weight:各类别的loss设置权值。
- ignore_index:忽略某个类别
- reduction:计算模式,可为none/sum/mean
- none-逐个元素计算(要注意这里每个神经元会算出一个loss,与上面CrossEntropy不同)
- sum-所有元素求和,返回标量
- mean-加权平均,返回标量
自动实现
使用Pytorch提供的nn.BCELoss函数
inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float) #注意这里的类型# 要注意这里target与神经元必须一一对应target_bce = target# itargetinputs = torch.sigmoid(inputs) # 因为要保证输入值取值在01区间,所以加上Sigmoidweights = torch.tensor([1, 1], dtype=torch.float)loss_f_none_w = nn.BCELoss(weight=weights, reduction='none')# forwardloss_none_w = loss_f_none_w(inputs, target_bce)# viewprint("\nweights: ", weights)print("BCE Loss", loss_none_w)
手动实现
idx = 0
x_i = inputs.detach().numpy()[idx, idx]
y_i = target.numpy()[idx, idx] #
# loss
# l_i = -[ y_i * np.log(x_i) + (1-y_i) * np.log(1-y_i) ] # np.log(0) = nan
l_i = -y_i * np.log(x_i) if y_i else -(1-y_i) * np.log(1-x_i)
# 输出loss
print("BCE inputs: ", inputs)
print("第一个loss为: ", l_i)
4. nn.BCEWithLogitsLoss
功能:结合Sigmoid与二分类交叉熵
注意事项:网络最后一层不能加sigmoid函数,在计算loss的时候会自动先加Sigmoid归一化再算loss。
因为有时候我们不想在最后一层使用Sigmoid,该方法就可以既实现归一化又避免在模型中添加Sigmoid。
数学公式: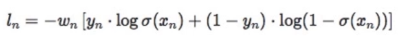
主要参数:
- pos_weight:正样本的权值
- weight:各类别的loss设置权值
- ignore_index:忽略某个类别
- reduction:计算模式,可为none/sum/mean
- none-逐个元素计算
- sum-所有元素求和,返回标量
- mean-加权平均,返回标量
5. nn.L1Loss
6. nn.MSELoss
7. nn.SmoothLlLoss
功能:平滑的L1Loss
其中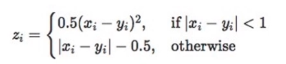
下面看示意图辅助理解公式: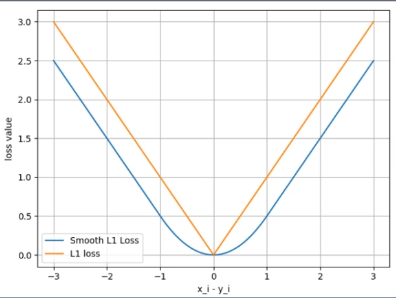
8. nn.PoissonNLLLoss
功能:泊松分布的负对数似然损失函数
主要参数:
- log_input:输入是否为对数形式,决定计算公式
- full:计算所有loss,默认为False
- eps:修正项,避免log(input)为nan,默认值为一个很小的数字:1e-08
计算公式:
- 当设置log_input为True,即输入已经是log形式时:
loss(input,target)=exp(input)-target * input
- 当设置log_input为False,即输入不是log形式时:
loss(input,target)=input-target* log(input+eps)
9. nn.KLDivLoss
功能:计算KLD(divergence),KL散度,就是相对熵,用来衡量两个分布之间的相似性(距离)。
因为上面讲过相对熵的数学计算公式为:
其中,P(x)表示真实分布的概率,也就是label;Q(x)表示模型输出的分布概率,要拟合真实分布。
而在Pytroch提供的nn.KLDivLoss方法中计算相对熵公式为: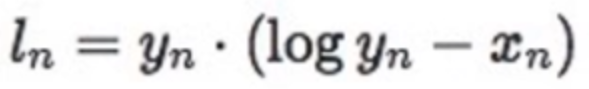
其中,表示label,
表示模型输出值。
对比两个公式我们可以发现,这里少了一个log。
所以在使用nn.KLDivLoss前,需要提前将输出计算log-probabilities,如通过nn.logsoftmax()
主要参数:
- reduction:none/sum/mean/batchmean
- batchmean-对batchsize维度求平均值(特殊)
10. nn.MarginRankingLoss
功能:计算两个向量之间的相似度,用于排序任务
计算公式: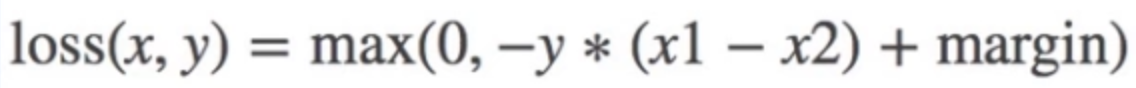
当y=1时,希望x1比x2大,当x1>x2时,不产生loss
当y=-1时,希望x2比x1大,当x2>x1时,不产生loss
注意:该方法计算两组数据之间每个元素的差异,返回一个n*n的loss 矩阵
x1 = torch.tensor([[1], [2], [3]], dtype=torch.float)
x2 = torch.tensor([[2], [2], [2]], dtype=torch.float)
target = torch.tensor([1, 1, -1], dtype=torch.float)
loss_f_none = nn.MarginRankingLoss(margin=0, reduction='none')
loss = loss_f_none(x1, x2, target)
运行结果:
11. nn.MultiLabelMarginLoss
功能:多标签边界损失函数,例如,多标签是指一张图片对应多个类别,不是多分类,多分类是一个图片属于一个类别,但是有多个类别。
目的:使是标签的神经元输出大于非标签的神经元输出
计算公式: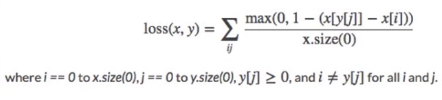
其中,分母是输出神经元的个数,分子中表示用label含有的神经元输出减去不是标签的神经元输出
自动实现
使用Pytroch提供的nn.MultiLabelMarginLoss方法,注意label类型为torch.long
x = torch.tensor([[0.1, 0.2, 0.4, 0.8]])
y = torch.tensor([[0, 3, -1, -1]], dtype=torch.long) # 标签是第0类和第3类,剩余的补-1
loss_f = nn.MultiLabelMarginLoss(reduction='none')
loss = loss_f(x, y)
print(loss) #0.8500
手动实现
x = x[0] # 选择第一个样本
item_1 = (1-(x[0] - x[1])) + (1 - (x[0] - x[2])) # [0]
item_2 = (1-(x[3] - x[1])) + (1 - (x[3] - x[2])) # [3]
loss_h = (item_1 + item_2) / x.shape[0]
print(loss_h)
四个神经元分别表示四个类别,标签[0, 3, -1, -1]表示标签是第0类和第3类
第2行中:item_1是将第0个神经元减去不是label的1和2号神经元:(1-(0.1-0.2))+(1-(0.1-0.4))=1.3
第3行中:item_2是将第3个神经元减去不是label的1和2号神经元:(1-(0.8-0.2))+(1-(0.8-0.4))=0.6
12. nn.SoftMarginLoss
13. nn.MultiLabelSoftMarginLoss
功能:SoftMarginLoss多标签版本
计算公式: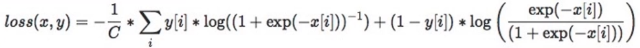
其中,C是标签的数量,label是0或1。当y=1(label为1)时用加号前的项计算Loss,当y=0时用后面的项计算Loss
主要参数:
- weight:各类别的loss设置权值
- reduction:计算模式,可为none/sum/mean
自动实现
注意这里是一组输出向量与一组标签向量求取loss返回的一个标量。inputs = torch.tensor([[0.3, 0.7, 0.8]]) target = torch.tensor([[0, 1, 1]], dtype=torch.float) loss_f = nn.MultiLabelSoftMarginLoss(reduction='none') loss = loss_f(inputs, target) print("MultiLabel SoftMargin: ", loss) #0.5429
标签向量[0, 1, 1]表示属于第1类和第2类,不属于第0类
14. nn.MultiMarginLoss
功能:计算多分类的折页损失
目的:为了让标签表示的类的神经元输出值大于非标签神经元的输出
计算公式: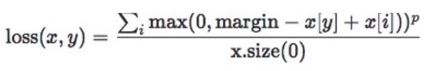

其中y是label,第几类就是第几个神经元;i表示非标签的神经元,并对i遍历。
主要参数:
- p:可选1或2,默认值为1
- weight:各类别的loss设置权值
- margin:边界值
- reduction:计算模式,可为none/sum/mean
自动实现
注意是一组输出向量计算一个loss。x = torch.tensor([[0.1, 0.2, 0.7], [0.2, 0.5, 0.3]]) # 2个样本 y = torch.tensor([1, 2], dtype=torch.long) # 注意类型 loss_f = nn.MultiMarginLoss(reduction='none') loss = loss_f(x, y) print("Multi Margin Loss: ", loss) # [0.8000, 0.7000]
15. nn.TripletMarginLoss
功能:计算三元组损失,人脸验证中常用。
目的:例如anchor和positive都是同一个人的人脸图像,negative是别人的人脸图像。该loss原理是使anchor与positive的输出值距离更近,与negative的距离更远,两者距离之差为margin。
计算公式:
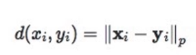
主要参数:
- p:范数的阶,默认为2
- margin:边界值,默认为1
- reduction:计算模式,可为none/sum/mean
自动实现
anchor = torch.tensor([[1.]]) pos = torch.tensor([[2.]]) neg = torch.tensor([[0.5]]) loss_f = nn.TripletMarginLoss(margin=1.0, p=1) loss = loss_f(anchor, pos, neg) print("Triplet Margin Loss", loss)
16. nn.HingeEmbeddingLoss
功能:计算两个输入的相似性,常用于非线性embedding和半监督学习
计算公式: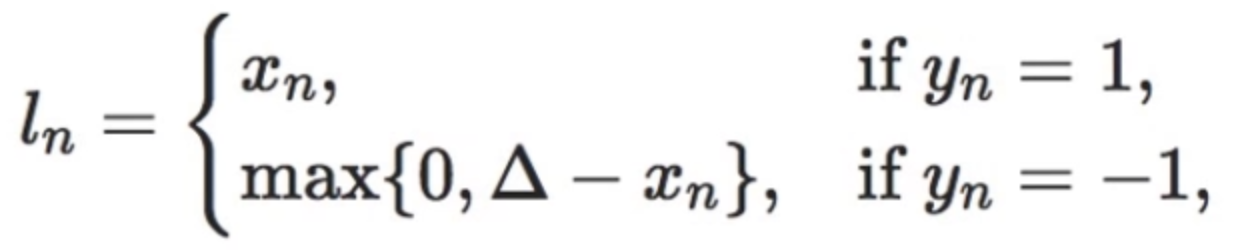
其中,表示margin边界值。
特别注意:输入x应为两个输入之差的绝对值。
主要参数:
- margin:边界值
- reduction:计算模式,可为none/sum/mean
自动实现
inputs = torch.tensor([[1., 0.8, 0.5]]) target = torch.tensor([[1, 1, -1]]) loss_f = nn.HingeEmbeddingLoss(margin=1, reduction='none') loss = loss_f(inputs, target) print("Hinge Embedding Loss", loss)
17. nn.CosineEmbeddingLoss
功能:采用余弦相似度计算两个输入的相似性,使用cos计算主要是为了关注的是方向上的差异。
计算公式: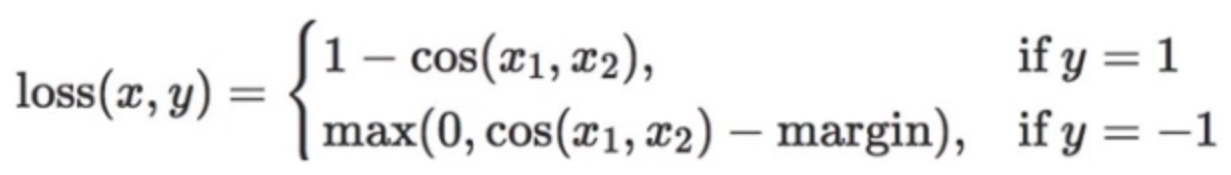
其中,
主要参数:
- margin:可取值[-1,1](因为cos的值域就是这个,所以margin不能设置太大),推荐为[0,0.5]
- reduction:计算模式,可为none/sum/mean
自动实现
x1 = torch.tensor([[0.3, 0.5, 0.7], [0.3, 0.5, 0.7]]) x2 = torch.tensor([[0.1, 0.3, 0.5], [0.1, 0.3, 0.5]]) target = torch.tensor([[1, -1]], dtype=torch.float) loss_f = nn.CosineEmbeddingLoss(margin=0., reduction='none') loss = loss_f(x1, x2, target) print("Cosine Embedding Loss", loss) # [0.0167, 0.9833]
18. nn.CTCLoss
功能:计算CTC损失,解决时序类数据的分类Connectionist Temporal Classification。
主要参数:
- blank:blank label
- zero infinity:无穷大的值或梯度置0
- reduction:计算模式,可为none/sum/mean
计算公式详见参考文献参考文献:
A.Graves et al.:Connectionist Temporal Classification:Labelling Unsegmented Sequence Data with Recurrent Neural Networks