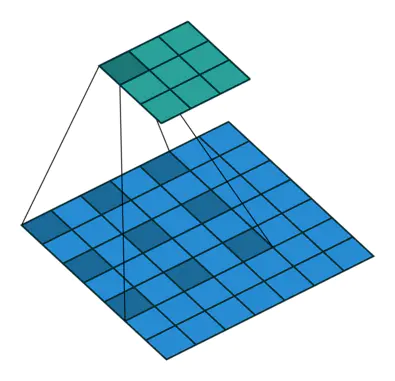
卷积

		
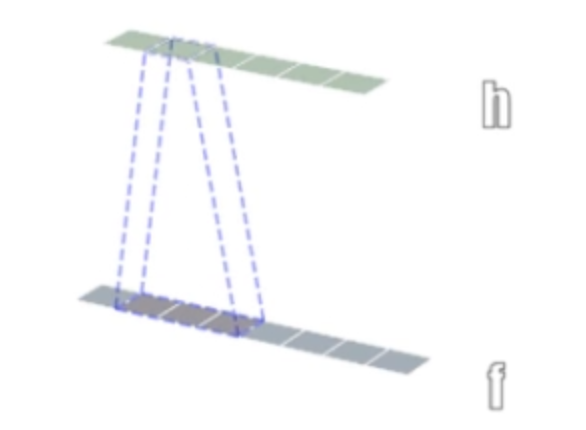
1维卷积	2维卷积	3维卷积

卷积维度：一般情况下，卷积核在几个维度上滑动，就是几维卷积。
而不能根据卷积核的维度来判断是几维卷积。

nn.Conv2d

功能：对多个二维信号进行二维卷积
主要参数：

• in_channels：输入通道数
• out_channels：输出通道数，等价于卷积核个数
• kernel_size：卷积核尺寸
• stride：步长
• padding：填充个数
• dilation：空洞卷积大小
• groups：分组卷积设置
• bias：偏置

空洞卷积

作用：可以增大感受野

分组卷积

分组卷积就类似AlexNet中将卷积分为两组，两组处理数据过程中不相互通讯，直到最后的FC才组合起来。

尺寸计算

简化版（不带padding和dilation）的计算公式：

考虑padding的计算公式：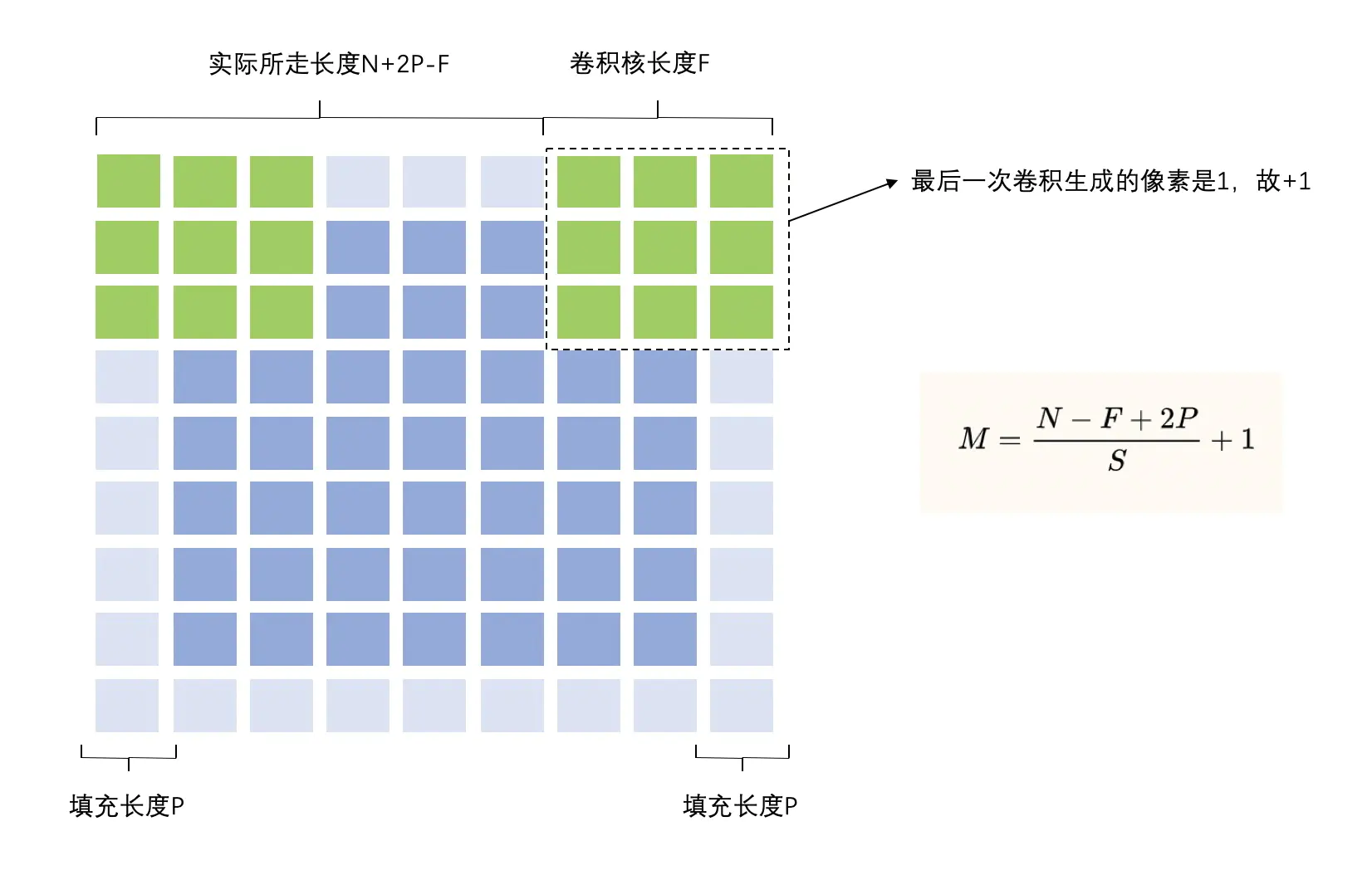

完整版（考虑padding和dilation）的计算公式：

代码实现

conv_layer = nn.Conv2d(3, 1, 3)   # input:(i, o, size) weights:(o, i , h, w)
nn.init.xavier_normal_(conv_layer.weight.data)
# calculation
img_conv = conv_layer(img_tensor)

上面nn.Conv2d初始化后，查看parameter字典中有一个4维张量weight，就是卷积核。
注意这里weight的shape代表含义为（o，i，h，w）

正常卷积的实现方法

假设图像尺寸为44_，卷积核为33_，padding=0，stride=1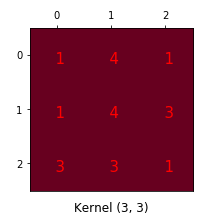

正常卷积操作过程：

1. 先把输入图像拉成一个1维矩阵：，其中16就是4*4个像素，1代表1张图片；

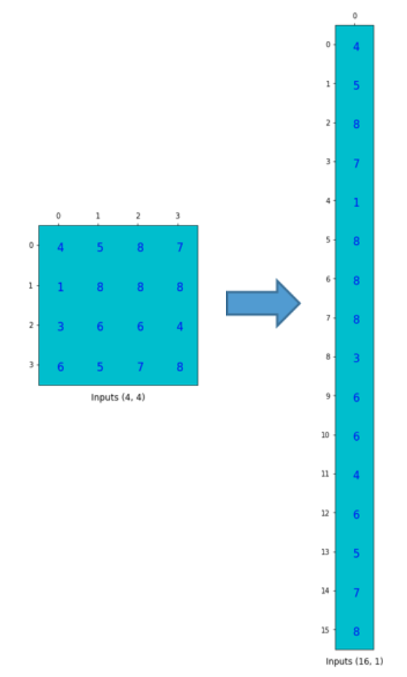
1. 把卷积核表示为矩阵：，其中16是卷积核3*3=9然后补0到16位（与上面输入图像像素总数一致），4是输出图像的像素总数，可通过上面公式计算得到；每一行的像素值是按如下方法得到的：

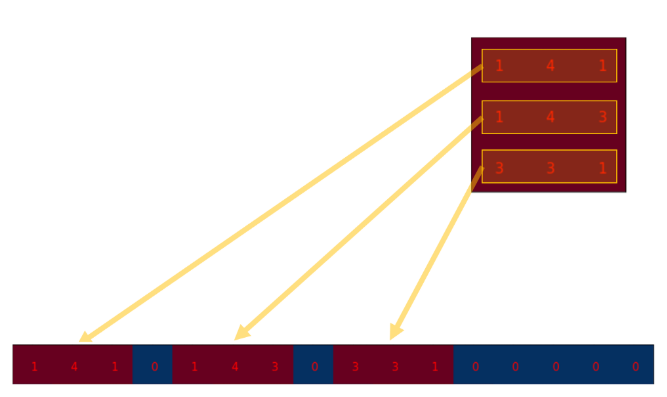
然后根据卷积的stride，可以得到每一行中卷积核的9个像素值如何分布：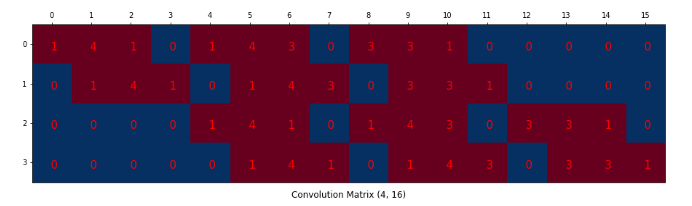

1. 输出特征图矩阵：，即卷积核矩阵与输入矩阵做点积

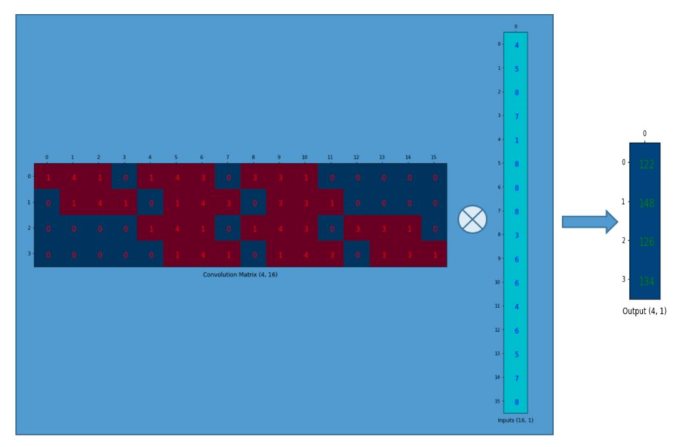
1. 最后再把输出矩阵reshape为2*2

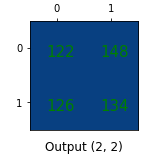
所以卷积矩阵就是对卷积核权值重新排列的矩阵，卷积运算可以通过使用卷积矩阵表示。

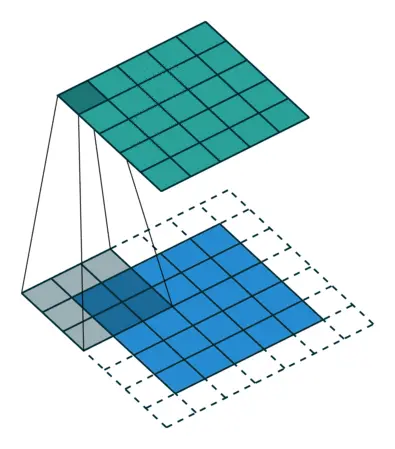
转置卷积

转置卷积又称为反卷积（这个名字一般不用，避免和信号处理里面的反卷积混淆）（Deconvolution）和部分跨越卷积（Fractionally strided Convolution），用于对图像进行上采样（UpSample）。

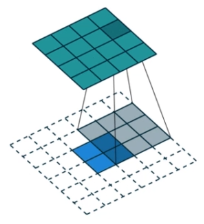
在上面正常卷积的操作流程中，我们知道通过使用卷积矩阵，可以使尺寸从16（44）到4（22）因为卷积矩阵是的。所以如果有一个的卷积矩阵，就可以使尺寸从4（22）到16（44）。另外我们还得得到1个像素值到9个像素值的关系：

转置卷积的实现方法

假设图像尺寸为22_，卷积核为33_，padding=0，stride=1

1. 同样地先将输入图像展开为1维矩阵：
2. 将卷积核构造为矩阵：，这里的4可以理解为：因为输入图像有4个像素，所以每次从卷积核最多挑选4个权值来与输入图像进行卷积。16就是输出图像的像素个数；所以每一列中有9个非零值，所以该转置卷积矩阵就能将输入图像中的1个像素值与输出图像中的9个像素值连接起来。

1. 输出特征图矩阵：

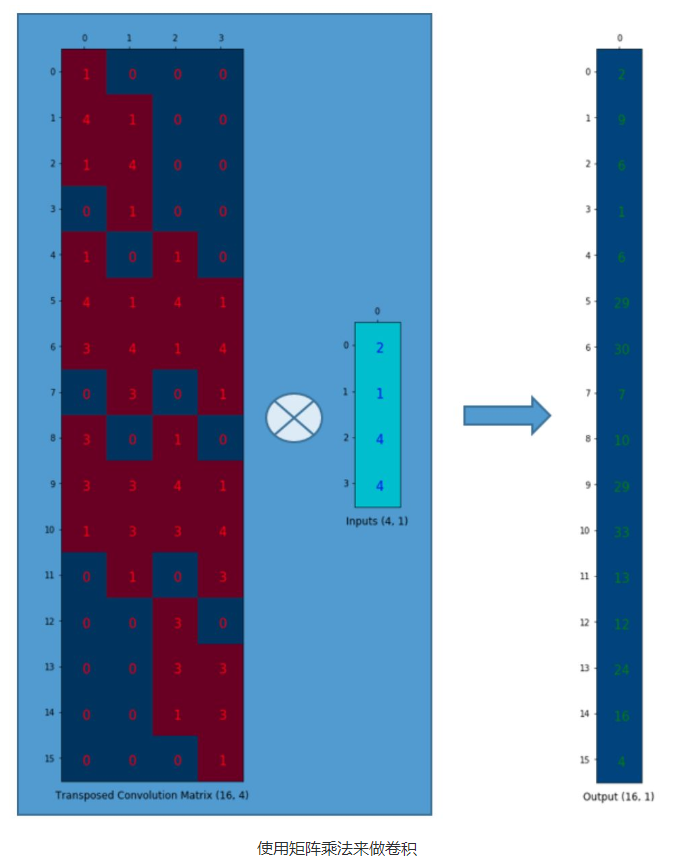
1. 最后将输出矩阵reshape为4*4矩阵

注意：转置卷积的卷积核矩阵在形状上与正常卷积的卷积核矩阵是转置关系，但是矩阵中的实际权值不一定是来自原始卷积矩阵的，它的权值是可以学习的，两者权值可能完全不同，所以两者是不可逆的，即4*4图像经过卷积和转置卷积后得到的16个像素是完全不同的，这也是不将转置卷积称作反卷积的原因。

nn.ConvTranspose2d

功能：转置卷积实现上采样
主要参数：

• in_channels：输入通道数
• out_channels：输出通道数
• kernel_size：卷积核尺寸
• stride：步长
• padding：填充个数
• dilation：空洞卷积大小
• groups：分组卷积设置
• bias：偏置

  尺寸计算

  简化版（不带padding和dilation）：
  
  完整版（考虑padding和dilation）：
  

总结：通过观察正常卷积和转置卷积的尺寸计算公式可以发现，两者其实是相反的。即正常卷积的input代入正常卷积公式计算出的output就是转置卷积的input，而正常卷积的input就是转置卷积的output。

代码实现

conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2)   # input:(i, o, size)
nn.init.xavier_normal_(conv_layer.weight.data)
# calculation
img_conv = conv_layer(img_tensor)

可视化后的特征图为：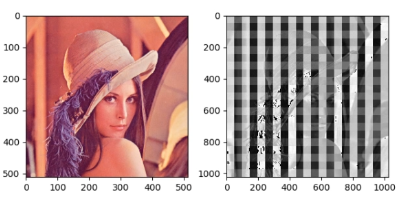

上述图像出现一格一格的图案被称作棋盘效应，这是转置卷积的通病，是由于不均匀重叠倒置的。
具体原因与解决方法见paper：《Deconvolution and Checkerboard Artifacts》