梯度消失与爆炸

根据链式法则求第二层权重的梯度有：

观察最后一项，因为，所以上式可转化为：

所以得到梯度消失的原因是：，所以；
梯度爆炸的原因是：，所以.

所以要避免梯度消失或者梯度爆炸就要控制网络层输出值的尺度范围，即不能太大或太小。

数学推导

梯度爆炸

根据上面推论我们知道要防止梯度爆炸就要控制网络层输出值的尺度范围，那么这里就用标准差来衡量尺度范围。
当没有激活函数时，且权值初始化为标准正态分布（即均值为0，方差为1）时，根据



可以推出：

通常的，X和Y初始化均满足各自的期望为0，即E(X)=0，E(Y)=0，则上式简化为：

因为在神经网络中，某个神经元（以第1层第1个为例）：

所以的方差为（n代表输入层有n个神经元）：

由于X和W初始化符合正态分布，因此其方差均为1，所以：

那么的标准差为

所以通过上面的推导我们知道，经过一层前向传播后，下一层网络层的输出值方差就是前一层输出值的n（前一层神经元个数）倍，标准差变大倍。所以经过很多层传播后，标准差会不断增大，超过可计算的范围变成NAN，也就是梯度爆炸了。

通过代码实验，创建神经元个数是400的FC层，结果验证了上面的推导是正确的。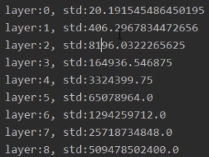

下面再来分析一下如何防止梯度爆炸，通过上面的推导我们知道网络隐藏层的输出值的方差和三个东西有关系：

即神经元个数，输入值的方差和权值的方差。
而要想让方差一直保持某一个范围尺度，就需要让网络层输出值的方差为1，这样经过多层传播后，不会产生梯度爆炸。上面的神经元个数n和网络层输入X都是我们不能设置的，唯一能让我们调节的就是超参数W了。如果我们设置权重初始化的方差如下：

并且最开始的输入值是满足标准正态分布的，所以就能使后面网络层输出值的方差为1.
通过代码实验结果如下：

nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))

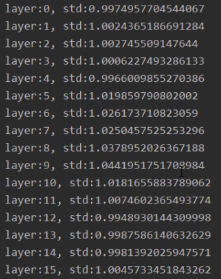
验证了上面权重初始化的方法是可以有效防止梯度爆炸的。

梯度消失

上面的网络结构中都没有考虑激活函数，如果我们加入tanh激活函数，就会发现标准差会变得越来越小，也就是数据变得越来越小，梯度会慢慢消失。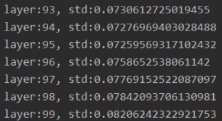

下面介绍一些针对上述问题的权值初始化方法。

Xavier初始化

参考文献：《Understanding the difficulty of training deep feedforward neural networks》
方差一致性：保持数据尺度维持在恰当范围，通常方差为1
适用激活函数：针对饱和函数，如Sigmoid，Tanh
参考文献中，同时考虑前向传播和反向传播的数据尺度问题推导出下面两个式子：


其中表示前一层的神经元个数，表示下一层的神经元个数。要满足上面式子就有：

通常Xavier初始化服从均匀分布，那么我们可以根据上式推导均匀分布的上下限。
假设W∼U[−a,a]（因为输入是0均值，所以上下限对称），那么W的方差为：

所以联立两式可以求得：

所以W~

手动实现

通常使用均匀分布

a = np.sqrt(6 / (self.neural_num + self.neural_num))  # 均匀分布上下限计算公式
tanh_gain = nn.init.calculate_gain('tanh')  # 计算tanh的增益，即数据输入后标准差的变化
a *= tanh_gain  # 这是最终均匀分布的尺度
nn.init.uniform_(m.weight.data, -a, a)  # 初始化

自动计算

Pytorch中nn.init提供了Xavier方法可以直接使用：

tanh_gain = nn.init.calculate_gain('tanh')
nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)

注意：Xavier方法只针对饱和函数，对非饱和函数不适用。例如将激活函数改为ReLu，层数增多时就会发生梯度爆炸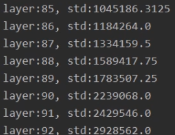

Kaiming初始化

参考文献：《Delving deep into rectifiers:Surpassing human-level performance on ImageNet classification》
同样遵循方差一致性原则：保持每一层网络层输出数据尺度维持在恰当范围，通常方差为1。
适用激活函数：ReLu及其变种
在参考文献中作者针对ReLu推导出要满足方差一致性，则

其中a是ReLu负半轴的斜率（普通ReLu负半轴斜率为0，变种的话就代入具体值）
是前一层网络层的神经元个数。

手动实现

通常使用正态分布

nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num))

自动计算

Pytorch中nn.init提供了Kaiming初始化方法可以直接使用：

nn.init.kaiming_normal_(m.weight.data)

常用初始化方法（十种四大类）

第一类：Xavier

1.Xavier均匀分布
2.Xavier标准正态分布

第二类：Kaiming

3.Kaiming均匀分布
4.Kaiming标准正态分布

第三类：常用分布

5.均匀分布
6.正态分布
7.常数分布

第四类：特殊矩阵

8.正交矩阵初始化
9.单位矩阵初始化
10.稀疏矩阵初始化

总结：初始化方法的选择要具体问题具体分析。但要注意的是无论选择哪种方法都要遵循方差一致性，即控制网络层输出值的方差在1附近。

nn.init.calculate_gain

这里补充一个上面代码使用到的特殊方法
主要功能：计算激活函数的方差变化尺度（就是激活函数输入值的方差与输出值的方差的比例，用于观察方差变化）
主要参数：

• nonlinearity：激活函数名称
• param：激活函数的参数，如Leaky ReLU的negative_slop

手动实现

x = torch.randn(10000)  # 构造输入数据
out = torch.tanh(x)
gain = x.std() / out.std()  # 计算尺度变化
print('gain:{}'.format(gain)) # 得到1.6

自动计算

即用Pytorch提供的nn.init.calculate_gain方法：

x = torch.randn(10000)  # 构造输入数据
out = torch.tanh(x)
tanh_gain = nn.init.calculate_gain('tanh')
print('tanh_gain in PyTorch:', tanh_gain)  # 得到1.667

我们知道tanh的尺度变化是1.6左右，即输入值经过tanh计算，方差会缩小1.6倍。这就是该方法的作用。